איתמר שטיין (שיחה | תרומות) (יצירת דף עם התוכן "==שאלה 1== ===סעיף ב=== ידוע כי <math>\liminf_{n\rightarrow \infty}(a_n \cdot n)>0</math> נניח ש <math>\liminf_{n\rightarrow \infty}(a_n \cd...") |
איתמר שטיין (שיחה | תרומות) (←סעיף ב) |
||
| (9 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 50: | שורה 50: | ||
נובע ממבחן ההשוואה לטורים חיוביים שגם הטור <math>\ \sum_{n=1}^\infty a_n</math> מתבדר. | נובע ממבחן ההשוואה לטורים חיוביים שגם הטור <math>\ \sum_{n=1}^\infty a_n</math> מתבדר. | ||
| + | |||
| + | ==שאלה 2== | ||
| + | |||
| + | ===סעיף א=== | ||
| + | |||
| + | טענת עזר: אם <math>A,B</math> קבוצות חסומות מלעיל אז | ||
| + | |||
| + | |||
| + | <math>\sup(A+B)=\sup(A)+\sup(B)</math> | ||
| + | |||
| + | |||
| + | הוכחה: נוכיח שהמספר <math>\sup(A)+\sup(B)</math> מקיים את התכונות של <math>\sup(A+B)</math> | ||
| + | |||
| + | * תכונה א': חסם מלעיל של <math>A+B</math>. הוכחה: | ||
| + | |||
| + | |||
| + | אם <math>x\in A+B</math> אז ניתן לכתוב <math>x=a+b</math> כאשר <math>a\in A, b\in B</math>. | ||
| + | |||
| + | היות ו <math>a\leq \sup(A)</math> ו <math>b\leq \sup(B)</math> מתקיים | ||
| + | |||
| + | <math>x=a+b\leq \sup(A)+\sup(B)</math> | ||
| + | |||
| + | |||
| + | * תכונה ב': החסם המלעיל הכי קטן. הוכחה: | ||
| + | |||
| + | יהי <math>y</math> איזשהוא חסם מלעיל של <math>A+B</math> | ||
| + | |||
| + | נניח בשלילה ש <math>y<\sup(A)+\sup(B)</math> | ||
| + | |||
| + | אז נקבל ש <math>y-\sup(B)<\sup(A)</math> | ||
| + | |||
| + | ולכן קיים <math>a\in A</math> כך ש <math>y-\sup(B)<a</math> | ||
| + | |||
| + | מכאן נקבל <math>y-a<\sup(B)</math> | ||
| + | |||
| + | ולכן קיים <math>b\in B</math> כך ש <math>y-a<b</math> | ||
| + | |||
| + | ולכן <math>y<a+b\in A+B</math> | ||
| + | |||
| + | בסתירה לכך ש <math>y</math> חסם מלעיל של <math>A+B</math> | ||
| + | |||
| + | לכן בהכרח מתקיים <math>\sup(A)+\sup(B)\leq y</math> | ||
| + | |||
| + | לסיכום: הוכחנו שהמספר <math>\sup(A)+\sup(B)</math> מקיים את שתי התכונות של חסם עליון | ||
| + | |||
| + | ולכן <math>\sup(A+B)=\sup(A)+\sup(B)</math>. מש"ל טענת עזר. | ||
| + | |||
| + | עכשיו קל להוכיח את הדרוש: | ||
| + | |||
| + | <math>\sup(A+B+C)=\sup(A+B)+\sup(C)=\sup(A)+\sup(B)+\sup(C)</math> | ||
| + | |||
| + | מש"ל. | ||
| + | |||
| + | ===סעיף ב=== | ||
| + | |||
| + | הפרכה פשוטה, ניקח <math>a_n=-\frac{1}{n}</math> ו <math>b_n=\frac{1}{n}</math> | ||
| + | |||
| + | מתקיים שלכל <math>n\in \mathbb{N}</math> | ||
| + | <math>a_n<b_n</math> | ||
| + | (ולכן בוודאי שזה מקיים כמעט לכל <math>n\in \mathbb{N}</math>). | ||
| + | |||
| + | אבל | ||
| + | |||
| + | <math>\lim_{n\rightarrow \infty}a_n=\lim_{n\rightarrow \infty}b_n=0</math> | ||
| + | |||
| + | |||
| + | שתי הערות: | ||
| + | א) כמעט לכל <math>n</math> פירושו: לכל <math>n</math> פרט למספר סופי של מקרים. | ||
| + | |||
| + | אן לחילופין: קיים <math>N\in \mathbb{N}</math> כך שהטענה מתקיימת לכל <math>n>N</math>. | ||
| + | |||
| + | ב) כמובן שהטענה הבאה נכונה | ||
| + | |||
| + | אם <math>a_n\leq b_n</math> ו | ||
| + | |||
| + | <math>\lim_{n\rightarrow \infty}a_n=a,\quad \lim_{n\rightarrow \infty}b_n=b</math> | ||
| + | |||
| + | אז | ||
| + | |||
| + | <math>a\leq b</math>. | ||
| + | |||
| + | |||
| + | ==שאלה 3== | ||
| + | |||
| + | ===סעיף א=== | ||
| + | |||
| + | <math>a_n=\frac{1}{\sqrt{n^2+1}} +\ldots + \frac{1}{\sqrt{n^2+n}}</math> | ||
| + | |||
| + | |||
| + | נשים לב שבסכום זה יש <math>n</math> מחוברים. כאשר מספר המחוברים תלוי ב <math>n</math> אי אפשר להשתמש באריתמטיקה של גבולות. | ||
| + | |||
| + | במקרה הזה נשתמש במשפט הסנדויץ. | ||
| + | |||
| + | נגדיר: | ||
| + | |||
| + | <math>b_n=\frac{1}{\sqrt{n^2+1}} +\ldots + \frac{1}{\sqrt{n^2+1}}=\frac{n}{\sqrt{n^2+1}}</math> | ||
| + | |||
| + | בגלל ש <math>n^2+1\leq n^2+i</math> (כאשר <math>1\leq i\leq n</math>) | ||
| + | |||
| + | ברור ש | ||
| + | |||
| + | <math>\frac{1}{\sqrt{n^2+i}}\leq \frac{1}{\sqrt{n^2+1}} </math> | ||
| + | |||
| + | ולכן <math>a_n\leq b_n</math> | ||
| + | |||
| + | בצורה דומה נגדיר | ||
| + | |||
| + | <math>c_n=\frac{1}{\sqrt{n^2+n}} +\ldots + \frac{1}{\sqrt{n^2+n}}=\frac{n}{\sqrt{n^2+n}}</math> | ||
| + | |||
| + | ויתקיים | ||
| + | |||
| + | <math>c_n\leq a_n</math> | ||
| + | |||
| + | <math>\lim_{n\rightarrow \infty} b_n = \lim_{n\rightarrow \infty}\frac{n}{\sqrt{n^2+1}} | ||
| + | =\lim_{n\rightarrow \infty}\frac{n}{n} \frac{1}{\sqrt{1+\frac{1}{n^2}}}=1 | ||
| + | </math> | ||
| + | |||
| + | ו | ||
| + | |||
| + | |||
| + | <math>\lim_{n\rightarrow \infty} c_n = \lim_{n\rightarrow \infty}\frac{n}{\sqrt{n^2+n}} | ||
| + | =\lim_{n\rightarrow \infty}\frac{n}{n} \frac{1}{\sqrt{1+\frac{1}{n}}}=1 | ||
| + | </math> | ||
| + | |||
| + | לכן לפי כלל הסנדויץ | ||
| + | |||
| + | <math>\lim_{n\rightarrow \infty} a_n=1</math> | ||
| + | |||
| + | |||
| + | ===סעיף ב=== | ||
| + | |||
| + | <math>a_{n+1}=\frac{(n-1)x_0 a_n}{n^2-1}</math> כאשר <math>a_2>0</math> ו <math>x_0>1</math>. | ||
| + | |||
| + | |||
| + | נשים לב ש | ||
| + | |||
| + | <math>\frac{(n-1)}{n^2-1}=\frac{n-1}{(n-1)(n+1)}=\frac{1}{n+1}</math> | ||
| + | |||
| + | ולכן | ||
| + | |||
| + | <math>a_{n+1}=\frac{x_0 a_n}{n+1}</math> | ||
| + | |||
| + | |||
| + | *טענה: לכל <math>n\in \mathbb{N}</math> מתקיים <math>a_n>0</math> | ||
| + | |||
| + | |||
| + | הוכחה: באינדוקציה, ידוע כבר כי <math>a_2>0</math> אבל אם <math>a_n>0</math> בהכרח יתקיים | ||
| + | |||
| + | <math>a_{n+1}>0</math> כי <math>x_0>0</math> ו <math>\frac{1}{n+1}>0</math>. | ||
| + | |||
| + | |||
| + | |||
| + | *טענה: עבור <math>n>x_0</math> מתקיים <math>a_{n+1}<a_n</math>. | ||
| + | |||
| + | כלומר הסדרה יורדת אם <math>n>x_0</math>. | ||
| + | |||
| + | הוכחה: אם <math>n>x_0</math> אז <math>\frac{x_0}{n+1}<1</math> ולכן | ||
| + | |||
| + | <math>a_{n+1}=\frac{x_0 a_n}{n+1}<a_n</math> (נשים לב שכאן משתמשים בכך ש <math>a_n>0</math>) | ||
| + | |||
| + | |||
| + | |||
| + | קיבלנו שהחל מ <math>N\in \mathbb{N}</math> כלשהוא, הסדרה היא מונוטונית יורדת וחסומה מלרע. | ||
| + | |||
| + | בגלל שמספר סופי של איברים לא משנה את גבול הסדרה, נקבל ש <math>a_n</math> מתכנסת (כי החל מנקודה מסוימת היא מונוטונית יורדת וחסומה מלרע). | ||
| + | |||
| + | נותר רק למצוא את גבולה. | ||
| + | |||
| + | נניח ש | ||
| + | |||
| + | <math>\lim_{n\rightarrow \infty}a_n=L</math> | ||
| + | |||
| + | וברור ש | ||
| + | |||
| + | <math>\lim_{n\rightarrow \infty} \frac{x_0}{n+1}=0</math> | ||
| + | |||
| + | ולכן מתקיים | ||
| + | |||
| + | <math>\lim_{n\rightarrow \infty} a_{n+1}=\lim_{n\rightarrow \infty}\frac{x_0}{n+1}\cdot \lim_{n\rightarrow \infty}a_n = 0\cdot L=0</math> | ||
| + | |||
| + | לכן הגבול הוא <math>0</math>. | ||
| + | |||
| + | |||
| + | ==שאלה 4== | ||
| + | |||
| + | ===סעיף א=== | ||
| + | ראשית נשים לב שמשפט לייבניץ לא עובד כאן. כי לייבניץ דורש (בין השאר) ש <math>a_n</math> היא סדרה מונוטונית יורדת. | ||
| + | |||
| + | את הטענה ניתן להפריך. | ||
| + | |||
| + | נבחר | ||
| + | |||
| + | <math>a_n=(-1)^{n+1}\frac{1}{n}</math> | ||
| + | |||
| + | |||
| + | אזי בוודאי מתקיים | ||
| + | |||
| + | <math>\lim_{n\rightarrow \infty} a_n=0</math> | ||
| + | |||
| + | אבל | ||
| + | |||
| + | <math>\sum_{n=1}^{\infty} (-1)^{n+1} a_n=\sum_{n=1}^{\infty}(-1)^{2n+2}\frac{1}{n}=\sum_{n=1}^{\infty}\frac{1}{n}</math> | ||
| + | |||
| + | שהוא טור מתבדר. | ||
| + | |||
| + | ===סעיף ב=== | ||
| + | *חלק א': | ||
| + | |||
| + | נשים לב שהטור | ||
| + | |||
| + | <math>\sum_{n=2}^{\infty}{(\frac{n-1}{n+1})}^{n(n-1)}</math> | ||
| + | |||
| + | הוא טור חיובי ולכן הוא מתכנס בהחלט אם ורק אם הוא מתכנס | ||
| + | |||
| + | נשתמש במבחן קושי להתכנסות טורים חיוביים: | ||
| + | |||
| + | נביט על הסדרה: | ||
| + | |||
| + | <math>\sqrt[n]{{(\frac{n-1}{n+1})}^{n(n-1)}}={(\frac{n-1}{n+1})}^{(n-1)}</math> | ||
| + | |||
| + | נחשב את הגבול | ||
| + | |||
| + | <math>\lim_{n\rightarrow \infty}{(\frac{n-1}{n+1})}^{(n-1)}=\lim_{n\rightarrow \infty}{(\frac{n-1}{n+1})}^{n+1} | ||
| + | \lim_{n\rightarrow \infty}{(\frac{n-1}{n+1})}^{-2} | ||
| + | =\lim_{n\rightarrow \infty}{(1-\frac{2}{n+1})}^{n+1} \lim_{n\rightarrow \infty}{(\frac{n+1}{n-1})}^2 | ||
| + | |||
| + | |||
| + | =e^{-2} \lim_{n\rightarrow \infty}{(1+\frac{2}{n-1})}^2 | ||
| + | =e^{-2} | ||
| + | <1 | ||
| + | </math> | ||
| + | |||
| + | (שימו לב ש | ||
| + | |||
| + | <math>\lim_{n\rightarrow \infty}{(1+\frac{x}{a_n})}^{a_n}=e^x</math> כאשר | ||
| + | <math>\lim_{n\rightarrow \infty}a_n=\infty</math> | ||
| + | ) | ||
| + | |||
| + | ולכן לפי מבחן קושי הטור מתכנס | ||
| + | |||
| + | *חלק ב | ||
| + | |||
| + | <math>\sum_{n=2}^{\infty}\frac{\sin(nx)}{{(\ln n)}^{\ln n}}</math> | ||
| + | |||
| + | זהו לא טור חיובי, ראשית נבדוק התכנסות בהחלט, כלומר נבדוק אם הטור | ||
| + | |||
| + | <math>\sum_{n=2}^{\infty}\frac{|\sin(nx)|}{{(\ln n)}^{\ln n}}</math> | ||
| + | |||
| + | מתכנס. | ||
| + | |||
| + | אנחנו נראה שהוא מתכנס. | ||
| + | |||
| + | ראשית, נשים לב ש | ||
| + | |||
| + | <math>|\sin(nx)|\leq 1</math> ולכן לפי מבחן ההשוואה לטורים חיוביים, מספיק להראות שהטור | ||
| + | |||
| + | <math>\sum_{n=2}^{\infty}\frac{1}{{(\ln n)}^{\ln n}}</math> | ||
| + | |||
| + | מתכנס. | ||
| + | |||
| + | היות ויש כאן הרבה <math>\ln</math>, אנו נרצה לנסות את מבחן העיבוי. | ||
| + | |||
| + | הסדרה <math>\frac{1}{{(\ln n)}^{\ln n}}</math> | ||
| + | |||
| + | היא מונוטונית, חיובית ושואפת ל <math>0</math>, ולכן ניתן להשתמש במבחן העיבוי. | ||
| + | |||
| + | נקבל שהטור | ||
| + | |||
| + | <math>\sum_{n=2}^{\infty}\frac{1}{{(\ln n)}^{\ln n}}</math> | ||
| + | |||
| + | מתכנס אם ורק אם הטור | ||
| + | |||
| + | <math>\sum_{n=2}^{\infty}2^n\frac{1}{{(\ln {2^n})}^{\ln {2^n}}}=\sum_{n=2}^{\infty}\frac{2^n}{{(n \ln 2)}^{n \ln 2}}</math> | ||
| + | |||
| + | זה טור חיובי, נבדוק את התכנסותו באמצעות מבחן קושי | ||
| + | |||
| + | נחשב את גבול הסדרה | ||
| + | |||
| + | <math>\sqrt[n]{\frac{2^n}{{(n \ln 2)}^{n \ln 2}}}</math> | ||
| + | |||
| + | ונקבל: | ||
| + | |||
| + | <math>\lim_{n\rightarrow \infty} {\frac{2}{{(n \ln 2)}^{ \ln 2}}}=0<1</math> | ||
| + | |||
| + | ולכן לפי מבחן קושי הטור מתכנס. | ||
| + | |||
| + | לפי כל השיקולים שהצגנו הטור המקורי מתכנס בהחלט ולכן בוודאי שהוא מתכנס. | ||
| + | |||
| + | ==שאלה 5== | ||
| + | ===סעיף א=== | ||
| + | נחשב את גבול הפונקציה בקצות הקטע: | ||
| + | |||
| + | <math>\lim_{x\rightarrow 1} x \sin (\frac{1}{x})+\frac{\sin x}{x}=1\sin 1 + \sin 1 = 2\sin 1</math> | ||
| + | |||
| + | היות והפונקציה רציפה ב <math>x=1</math> בוודאי שיש לה שם גבול. | ||
| + | |||
| + | כמו כן: | ||
| + | |||
| + | <math>\lim_{x\rightarrow 0} x \sin (\frac{1}{x})=0</math> | ||
| + | |||
| + | כי <math>\lim_{x\rightarrow 0} x =0</math> ו <math>\sin (\frac{1}{x})</math> היא פונקציה חסומה. | ||
| + | |||
| + | ו | ||
| + | |||
| + | <math>\lim_{x\rightarrow 0} \frac{\sin x}{x} = 1</math> | ||
| + | |||
| + | ולכן לפונקציה קיים גבול גם ב <math>x=0</math>. | ||
| + | |||
| + | זאת פונקציה רציפה ב <math>(0,1)</math> שהגבולות שלה בקצות הקטע קיימים ולכן היא רציפה במידה שווה על הקטע <math>(0,1)</math>. | ||
| + | |||
| + | ===סעיף ב=== | ||
| + | נשים לב ש | ||
| + | |||
| + | <math>\frac{1}{n} \sum_{i=1}^n f(x_i)</math> | ||
| + | |||
| + | זה ממוצע של הערכים | ||
| + | |||
| + | <math>f(x_1),\ldots , f(x_n)</math> | ||
| + | |||
| + | מבין הערכים האלה חייב להיות מינימום ומקסימום. | ||
| + | |||
| + | כלומר קיימים <math>i_0,i_1</math> עבורם | ||
| + | |||
| + | <math>f(x_{i_0})=\min\{f(x_1),\ldots , f(x_n)\},\quad f(x_{i_1})=\max\{f(x_1),\ldots , f(x_n)\}</math> | ||
| + | |||
| + | ואז נקבל | ||
| + | |||
| + | <math>\frac{1}{n} \sum_{i=1}^n f(x_i)\leq \frac{1}{n} \sum_{i=1}^n f(x_{i_1}) = f(x_{i_1})</math> | ||
| + | |||
| + | ובאופן דומה | ||
| + | |||
| + | <math>\frac{1}{n} \sum_{i=1}^n f(x_i)\geq \frac{1}{n} \sum_{i=1}^n f(x_{i_0}) = f(x_{i_0})</math> | ||
| + | |||
| + | נניח בלי הגבלת כלליות ש | ||
| + | <math>x_{i_0}<x_{i_1}</math> | ||
| + | |||
| + | ראינו שהערך | ||
| + | <math>\sum_{i=1}^n f(x_i)</math> | ||
| + | |||
| + | נמצא בין <math>f(x_{i_0})</math> ל <math>f(x_{i_1})</math> | ||
| + | |||
| + | וברור ש <math>f</math> | ||
| + | רציפה על | ||
| + | <math>[x_{i_0},x_{i_1}]</math> | ||
| + | |||
| + | לכן לפי משפט ערך הביניים קיים | ||
| + | |||
| + | <math>c\in (x_{i_0},x_{i_2})\subseteq (a,b)</math> | ||
| + | |||
| + | כך ש: | ||
| + | |||
| + | <math>f(c)=\sum_{i=1}^n f(x_i)</math> | ||
| + | |||
| + | וזה מראה את מה שנדרש | ||
| + | |||
| + | ==שאלה 6== | ||
| + | === סעיף א=== | ||
| + | |||
| + | לפי משפט לגרנז', קיימת <math>d\in (a,c)</math> | ||
| + | |||
| + | כך ש | ||
| + | |||
| + | <math>f'(d)=\frac{f(c)-f(a)}{c-a}=\frac{f(c)}{c-a}>0</math> | ||
| + | |||
| + | וקיימת <math>e\in (c,b)</math> | ||
| + | |||
| + | כך ש | ||
| + | |||
| + | <math>f'(e)=\frac{f(b)-f(c)}{b-c}=\frac{-f(c)}{b-c}<0</math> | ||
| + | |||
| + | לפי משפט לגרנז' על הפונקציה <math>f'</math>, קיימת <math>t\in (d,e)\subseteq (a,b)</math> | ||
| + | |||
| + | כך ש | ||
| + | |||
| + | <math>f''(t)=\frac{f'(e)-f'(d)}{e-d}</math> | ||
| + | |||
| + | נשים לב ש <math>f'(e)<0,\quad f'(d)>0</math> ו <math>e>d</math> ולכן ברור ש | ||
| + | |||
| + | <math>f''(t)<0</math> | ||
| + | |||
| + | כנדרש | ||
| + | |||
| + | ===סעיף ב=== | ||
| + | |||
| + | נשתמש במשפט לגרנז' על הפונקציה | ||
| + | |||
| + | <math>f(x)=\ln(x+1)</math> על הקטע <math>[a,b]</math> (בגלל ש <math>b>a>0</math>, הפונקציה מוגדרת וגזירה בקטע זה.) | ||
| + | |||
| + | נזכור כי | ||
| + | |||
| + | <math>f'(x)=\frac{1}{x+1}</math> | ||
| + | |||
| + | ולכן לפי לגרנז' קיימת <math>c\in(a,b)</math> כך ש | ||
| + | |||
| + | <math>\frac{\ln(b+1)-\ln(a+1)}{b-a}=\frac{1}{c+1}</math> | ||
| + | |||
| + | בגלל ש <math>a<c<b</math>, ברור ש | ||
| + | |||
| + | <math>\frac{1}{b+1}<\frac{1}{c+1}<\frac{1}{a+1}</math> | ||
| + | |||
| + | ולכן | ||
| + | |||
| + | <math>\frac{1}{b+1}<\frac{\ln(b+1)-\ln(a+1)}{b-a}<\frac{1}{a+1}</math> | ||
| + | |||
| + | כלומר | ||
| + | |||
| + | <math>\frac{b-a}{b+1}<\ln(b+1)-\ln(a+1)<\frac{b-a}{a+1}</math> | ||
| + | |||
| + | כלומר | ||
| + | |||
| + | <math>\frac{b-a}{b+1}<\ln(\frac{b+1}{a+1})<\frac{b-a}{a+1}</math> | ||
| + | |||
| + | שזה מה שרצינו להראות | ||
גרסה אחרונה מ־06:52, 1 בפברואר 2013
שאלה 1
סעיף ב
ידוע כי
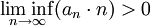
נניח ש
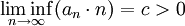
נסמן 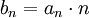
כלומר
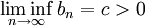
טענת עזר: קיים 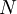 כך שאם
כך שאם 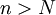 אז
אז 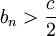
(במילים אחרות: יש רק מספר סופי של איברים ב  שיותר קטנים מ
שיותר קטנים מ 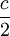 )
)
הוכחה: נניח בשלילה שזה לא נכון, כלומר קיימים אינסוף איברים מ  שעבורם
שעבורם 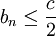
אז קיימת תת סדרה 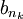 כך ש
כך ש 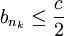 לכל
לכל 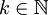
נשים לב ש  היא חסומה מלרע ולכן
היא חסומה מלרע ולכן 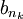 חסומה גם מלעיל וגם מלרע.
חסומה גם מלעיל וגם מלרע.
לכן ל 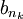 יש תת סדרה מתכנסת
יש תת סדרה מתכנסת 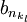 כך ש
כך ש
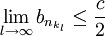
וזאת בסתירה לכך ש 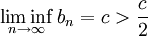
זה מוכיח את טענת העזר.
כעת, אנחנו יודעים שהחל מ 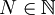 כלשהוא מתקיים
כלשהוא מתקיים
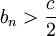
אבל בגלל ש 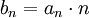 זה אומר שהחל מאותו
זה אומר שהחל מאותו 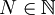 מתקיים
מתקיים
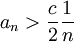
בגלל שהטור
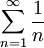 מתבדר
מתבדר
נובע ממבחן ההשוואה לטורים חיוביים שגם הטור 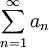 מתבדר.
מתבדר.
שאלה 2
סעיף א
טענת עזר: אם 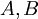 קבוצות חסומות מלעיל אז
קבוצות חסומות מלעיל אז
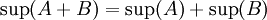
הוכחה: נוכיח שהמספר 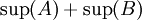 מקיים את התכונות של
מקיים את התכונות של 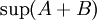
- תכונה א': חסם מלעיל של
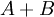 . הוכחה:
. הוכחה:
אם 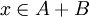 אז ניתן לכתוב
אז ניתן לכתוב 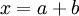 כאשר
כאשר 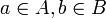 .
.
היות ו 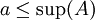 ו
ו 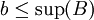 מתקיים
מתקיים
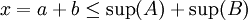
- תכונה ב': החסם המלעיל הכי קטן. הוכחה:
יהי  איזשהוא חסם מלעיל של
איזשהוא חסם מלעיל של 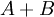
נניח בשלילה ש 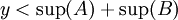
אז נקבל ש 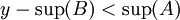
ולכן קיים 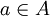 כך ש
כך ש 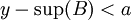
מכאן נקבל 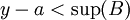
ולכן קיים 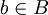 כך ש
כך ש 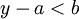
ולכן 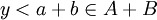
בסתירה לכך ש  חסם מלעיל של
חסם מלעיל של 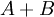
לכן בהכרח מתקיים 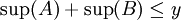
לסיכום: הוכחנו שהמספר 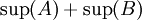 מקיים את שתי התכונות של חסם עליון
מקיים את שתי התכונות של חסם עליון
ולכן 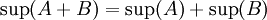 . מש"ל טענת עזר.
. מש"ל טענת עזר.
עכשיו קל להוכיח את הדרוש:
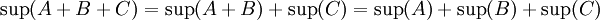
מש"ל.
סעיף ב
הפרכה פשוטה, ניקח 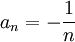 ו
ו 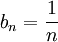
מתקיים שלכל 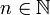
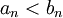 (ולכן בוודאי שזה מקיים כמעט לכל
(ולכן בוודאי שזה מקיים כמעט לכל 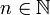 ).
).
אבל
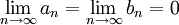
שתי הערות:
א) כמעט לכל  פירושו: לכל
פירושו: לכל  פרט למספר סופי של מקרים.
פרט למספר סופי של מקרים.
אן לחילופין: קיים 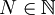 כך שהטענה מתקיימת לכל
כך שהטענה מתקיימת לכל 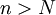 .
.
ב) כמובן שהטענה הבאה נכונה
אם 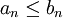 ו
ו
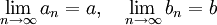
אז
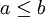 .
.
שאלה 3
סעיף א
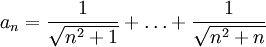
נשים לב שבסכום זה יש  מחוברים. כאשר מספר המחוברים תלוי ב
מחוברים. כאשר מספר המחוברים תלוי ב  אי אפשר להשתמש באריתמטיקה של גבולות.
אי אפשר להשתמש באריתמטיקה של גבולות.
במקרה הזה נשתמש במשפט הסנדויץ.
נגדיר:
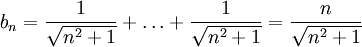
בגלל ש 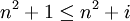 (כאשר
(כאשר 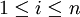 )
)
ברור ש
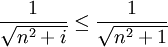
ולכן 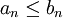
בצורה דומה נגדיר
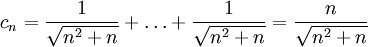
ויתקיים
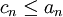
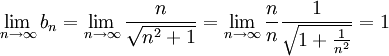
ו
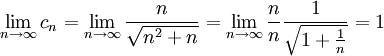
לכן לפי כלל הסנדויץ
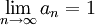
סעיף ב
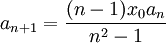 כאשר
כאשר 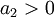 ו
ו 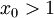 .
.
נשים לב ש
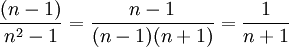
ולכן
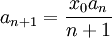
- טענה: לכל
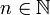 מתקיים
מתקיים 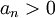
הוכחה: באינדוקציה, ידוע כבר כי 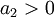 אבל אם
אבל אם 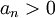 בהכרח יתקיים
בהכרח יתקיים
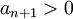 כי
כי 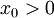 ו
ו 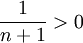 .
.
- טענה: עבור
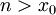 מתקיים
מתקיים 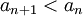 .
.
כלומר הסדרה יורדת אם 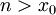 .
.
הוכחה: אם 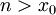 אז
אז 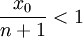 ולכן
ולכן
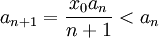 (נשים לב שכאן משתמשים בכך ש
(נשים לב שכאן משתמשים בכך ש 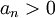 )
)
קיבלנו שהחל מ 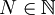 כלשהוא, הסדרה היא מונוטונית יורדת וחסומה מלרע.
כלשהוא, הסדרה היא מונוטונית יורדת וחסומה מלרע.
בגלל שמספר סופי של איברים לא משנה את גבול הסדרה, נקבל ש  מתכנסת (כי החל מנקודה מסוימת היא מונוטונית יורדת וחסומה מלרע).
מתכנסת (כי החל מנקודה מסוימת היא מונוטונית יורדת וחסומה מלרע).
נותר רק למצוא את גבולה.
נניח ש
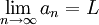
וברור ש
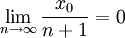
ולכן מתקיים
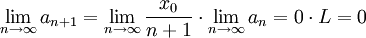
לכן הגבול הוא  .
.
שאלה 4
סעיף א
ראשית נשים לב שמשפט לייבניץ לא עובד כאן. כי לייבניץ דורש (בין השאר) ש  היא סדרה מונוטונית יורדת.
היא סדרה מונוטונית יורדת.
את הטענה ניתן להפריך.
נבחר
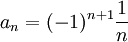
אזי בוודאי מתקיים
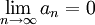
אבל
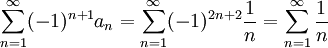
שהוא טור מתבדר.
סעיף ב
- חלק א':
נשים לב שהטור
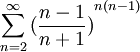
הוא טור חיובי ולכן הוא מתכנס בהחלט אם ורק אם הוא מתכנס
נשתמש במבחן קושי להתכנסות טורים חיוביים:
נביט על הסדרה:
![\sqrt[n]{{(\frac{n-1}{n+1})}^{n(n-1)}}={(\frac{n-1}{n+1})}^{(n-1)}](/images/math/3/d/7/3d71ec013ef7946df49ffd1c1aa9d606.png)
נחשב את הגבול
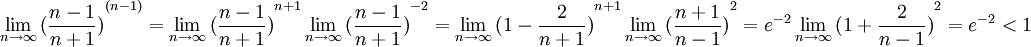
(שימו לב ש
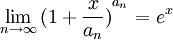 כאשר
כאשר
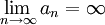 )
)
ולכן לפי מבחן קושי הטור מתכנס
- חלק ב
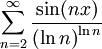
זהו לא טור חיובי, ראשית נבדוק התכנסות בהחלט, כלומר נבדוק אם הטור
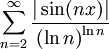
מתכנס.
אנחנו נראה שהוא מתכנס.
ראשית, נשים לב ש
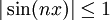 ולכן לפי מבחן ההשוואה לטורים חיוביים, מספיק להראות שהטור
ולכן לפי מבחן ההשוואה לטורים חיוביים, מספיק להראות שהטור
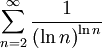
מתכנס.
היות ויש כאן הרבה 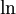 , אנו נרצה לנסות את מבחן העיבוי.
, אנו נרצה לנסות את מבחן העיבוי.
הסדרה 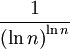
היא מונוטונית, חיובית ושואפת ל  , ולכן ניתן להשתמש במבחן העיבוי.
, ולכן ניתן להשתמש במבחן העיבוי.
נקבל שהטור
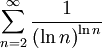
מתכנס אם ורק אם הטור
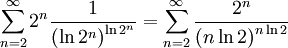
זה טור חיובי, נבדוק את התכנסותו באמצעות מבחן קושי
נחשב את גבול הסדרה
![\sqrt[n]{\frac{2^n}{{(n \ln 2)}^{n \ln 2}}}](/images/math/e/c/1/ec19d621378c9472be0ecb706cf2ce69.png)
ונקבל:
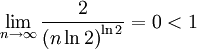
ולכן לפי מבחן קושי הטור מתכנס.
לפי כל השיקולים שהצגנו הטור המקורי מתכנס בהחלט ולכן בוודאי שהוא מתכנס.
שאלה 5
סעיף א
נחשב את גבול הפונקציה בקצות הקטע:
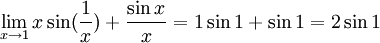
היות והפונקציה רציפה ב 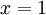 בוודאי שיש לה שם גבול.
בוודאי שיש לה שם גבול.
כמו כן:
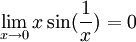
כי 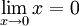 ו
ו 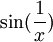 היא פונקציה חסומה.
היא פונקציה חסומה.
ו
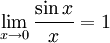
ולכן לפונקציה קיים גבול גם ב 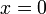 .
.
זאת פונקציה רציפה ב 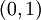 שהגבולות שלה בקצות הקטע קיימים ולכן היא רציפה במידה שווה על הקטע
שהגבולות שלה בקצות הקטע קיימים ולכן היא רציפה במידה שווה על הקטע 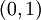 .
.
סעיף ב
נשים לב ש
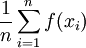
זה ממוצע של הערכים
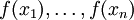
מבין הערכים האלה חייב להיות מינימום ומקסימום.
כלומר קיימים 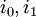 עבורם
עבורם

ואז נקבל
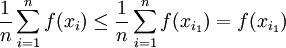
ובאופן דומה
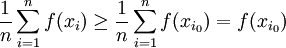
נניח בלי הגבלת כלליות ש
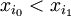
ראינו שהערך
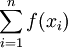
נמצא בין 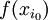 ל
ל 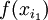
וברור ש  רציפה על
רציפה על
![[x_{i_0},x_{i_1}]](/images/math/d/e/c/decf35065e8fca080ef3bb8107d8f8f5.png)
לכן לפי משפט ערך הביניים קיים
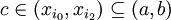
כך ש:
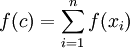
וזה מראה את מה שנדרש
שאלה 6
סעיף א
לפי משפט לגרנז', קיימת 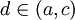
כך ש
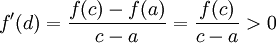
וקיימת 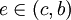
כך ש
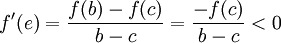
לפי משפט לגרנז' על הפונקציה 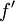 , קיימת
, קיימת 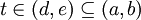
כך ש
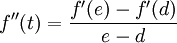
נשים לב ש  ו
ו 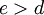 ולכן ברור ש
ולכן ברור ש
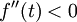
כנדרש
סעיף ב
נשתמש במשפט לגרנז' על הפונקציה
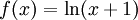 על הקטע
על הקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) (בגלל ש
(בגלל ש 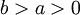 , הפונקציה מוגדרת וגזירה בקטע זה.)
, הפונקציה מוגדרת וגזירה בקטע זה.)
נזכור כי
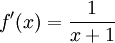
ולכן לפי לגרנז' קיימת 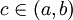 כך ש
כך ש
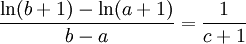
בגלל ש 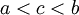 , ברור ש
, ברור ש
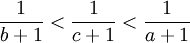
ולכן
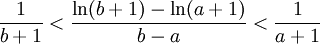
כלומר
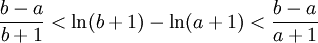
כלומר
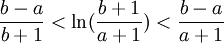
שזה מה שרצינו להראות