הבדלים בין גרסאות בדף "88-132 סמסטר א' תשעא/ פתרון מועד ב'"
| שורה 10: | שורה 10: | ||
לכן, עבור <math>\frac{1}{n}</math> קיימת תת סדרה המתכנסת למספר הקרוב לr עד כדי <math>\frac{1}{n}</math>. לכן קיים בסדרה הזו מקום אשר החל ממנו והלאה כל האיברים קרובים לr עד כדי <math>2/n</math> (המרחק בין גבול תת הסדרה לבין r ועוד מרחק בין איברי תת הסדרה לגבול תת הסדרה). | לכן, עבור <math>\frac{1}{n}</math> קיימת תת סדרה המתכנסת למספר הקרוב לr עד כדי <math>\frac{1}{n}</math>. לכן קיים בסדרה הזו מקום אשר החל ממנו והלאה כל האיברים קרובים לr עד כדי <math>2/n</math> (המרחק בין גבול תת הסדרה לבין r ועוד מרחק בין איברי תת הסדרה לגבול תת הסדרה). | ||
נבחר איברים כאלה מתתי הסדרות, ובלבד שכל איבר יהיה אחרי האיבר הקודם. כך בנינו סדרה שאיבריה קרובים מרחק <math>2/n</math> מr ולכן היא וודאי מתכנסת לr כפי שרצינו. | נבחר איברים כאלה מתתי הסדרות, ובלבד שכל איבר יהיה אחרי האיבר הקודם. כך בנינו סדרה שאיבריה קרובים מרחק <math>2/n</math> מr ולכן היא וודאי מתכנסת לr כפי שרצינו. | ||
| + | |||
| + | ==שאלה 2== | ||
| + | בדוק התכנסות של הטורים הבאים: | ||
| + | |||
| + | ===א=== | ||
| + | <math>\sum (-1)^n\tan{\frac{1}{n}}</math> | ||
| + | |||
| + | נבדוק התכנסות בהחלט, נוכיח שהטור חבר של הטור ההרמוני: | ||
| + | |||
| + | <math>\lim\frac{\tan\frac{1}{n}}{\frac{1}{n}}=\lim\frac{\sin{\frac{1}{n}}}{\frac{1}{n}\cos\frac{1}{n}}=1</math> | ||
| + | |||
| + | ולכן הוא אינו מתכנס בהחלט. | ||
| + | |||
| + | קל לראות שtan מונוטונית באיזור אפס (נגזרתה חיובית בלבד), וכמו כן <math>tan(0)=0</math> והיא רציפה שם ולכן סה"כ יש לנו סדרה המתכנסת מונוטונית לאפס ולפי משפט לייבניץ הטור כולו מתכנס בתנאי. | ||
גרסה מ־20:24, 10 במרץ 2011
תוכן עניינים
המבחן של פרופ' זלצמן
שאלה 1
תהי סדרה a_n, ותהי E קבוצות הגבולות החלקיים שלה. הוכח/הפרך: E סגורה
הוכחה
על מנת להוכיח שE סגורה, יש להוכיח שהיא מכילה את כל נקודות ההצטברות שלה. כלומר, אם r היא נקודת הצטברות של E אזי היא גם גבול חלקי של E.
נניח r נקודת הצטברות של E, לכן לכל אפסילון גדול מאפס קיים גבול חלקי הקרוב לr עד כדי אפסילון, ולכל גבול חלקי כזה קיימת תת סדרה המתכנסת אליו.
לכן, עבור  קיימת תת סדרה המתכנסת למספר הקרוב לr עד כדי
קיימת תת סדרה המתכנסת למספר הקרוב לr עד כדי  . לכן קיים בסדרה הזו מקום אשר החל ממנו והלאה כל האיברים קרובים לr עד כדי
. לכן קיים בסדרה הזו מקום אשר החל ממנו והלאה כל האיברים קרובים לr עד כדי 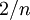 (המרחק בין גבול תת הסדרה לבין r ועוד מרחק בין איברי תת הסדרה לגבול תת הסדרה).
נבחר איברים כאלה מתתי הסדרות, ובלבד שכל איבר יהיה אחרי האיבר הקודם. כך בנינו סדרה שאיבריה קרובים מרחק
(המרחק בין גבול תת הסדרה לבין r ועוד מרחק בין איברי תת הסדרה לגבול תת הסדרה).
נבחר איברים כאלה מתתי הסדרות, ובלבד שכל איבר יהיה אחרי האיבר הקודם. כך בנינו סדרה שאיבריה קרובים מרחק 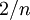 מr ולכן היא וודאי מתכנסת לr כפי שרצינו.
מr ולכן היא וודאי מתכנסת לr כפי שרצינו.
שאלה 2
בדוק התכנסות של הטורים הבאים:
א
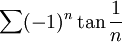
נבדוק התכנסות בהחלט, נוכיח שהטור חבר של הטור ההרמוני:
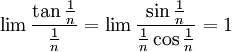
ולכן הוא אינו מתכנס בהחלט.
קל לראות שtan מונוטונית באיזור אפס (נגזרתה חיובית בלבד), וכמו כן 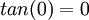 והיא רציפה שם ולכן סה"כ יש לנו סדרה המתכנסת מונוטונית לאפס ולפי משפט לייבניץ הטור כולו מתכנס בתנאי.
והיא רציפה שם ולכן סה"כ יש לנו סדרה המתכנסת מונוטונית לאפס ולפי משפט לייבניץ הטור כולו מתכנס בתנאי.