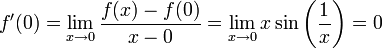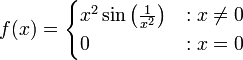הבדלים בין גרסאות בדף "88-132 סמסטר א' תשעא/ פתרון מועד ב'"
יהודה שמחה (שיחה | תרומות) |
יהודה שמחה (שיחה | תרומות) |
||
| שורה 42: | שורה 42: | ||
זהה וסווג נקודות אי־רציפות: | זהה וסווג נקודות אי־רציפות: | ||
===א=== | ===א=== | ||
| − | <math>(x^2-1) | + | <math>(x^2-1)\sin\left(\frac1{x^3-x^2}\right)</math> |
| − | נקודות | + | נקודות אי־הרציפות הן כאשר המכנה מתאפס, כלומר <math>0,1</math> . ב־<math>0^+</math> , <math>\frac{1}{x^3-x^2}\to -\infty</math> . מכיון שזו פונקציה רציפה ששואפת לאינסוף, הסינוס מקבל עליה אינסוף מחזורים ולכן אין לו גבול. <math>x^2-1\to -1</math> ולכן סה"כ יש לנו פונקציה עם גבול סופי שונה מ־<math>0</math> גבול פונקציה ללא גבול ולכן לא קיים הגבול החד־צדדי ולכן נקודת אי־הרציפות <math>0</math> הנה '''ממין שני'''. |
| − | בנקודה <math>1</math> אנחנו מקבלים פונקציה ששואפת | + | בנקודה <math>1</math> אנחנו מקבלים פונקציה ששואפת ל־<math>0</math> כפול חסומה' ולכן סה"כ יש שאיפה ל־<math>0</math> וזו נקודת אי־רציפות סליקה. |
===ב=== | ===ב=== | ||
<math>f(x)=\big\lfloor|x|\big\rfloor</math> | <math>f(x)=\big\lfloor|x|\big\rfloor</math> | ||
| − | נניח ש[x] הוא המספר השלם הגדול ביותר שקטן או שווה | + | נניח ש[x] הוא המספר השלם הגדול ביותר שקטן או שווה ל־<math>x</math> . אזי עבור <math>|x|<1</math> מתקיים <math>f(x)=0</math> ולכן שם הפונקציה רציפה. עבור <math>1<|x|<2</math> מתקיים <math>f(x)=1</math> ולכן <math>x=\pm 1</math> הנן נקודות אי־רציפות ממין ראשון (הגבול הוא <math>1</math> מצד אחד ו־<math>0</math> מהצד השני). באופן דומה לכל <math>n</math> טבעי מתקיים ש<math>\pm n</math> הן נקודות אי-רציפות מ'''מין ראשון'''. |
===ג=== | ===ג=== | ||
| − | <math>\tan\left(\ | + | <math>\tan\left(\frac{1}{\log(x^2)}\right)</math> |
| − | + | ב־<math>0</math> , הלוגריתם שואף ל־<math>-\infty</math> ולכן <math>\frac{1}{\log(x^2)}\to 0</math> ולכן הגבול כולו הוא <math>0</math> וזו נקודת אי־רציפות '''סליקה'''. | |
| − | + | ב־<math>\pm1</math> הלוגריתם שואף ל־<math>0</math> ולכן מצד אחד <math>\frac{1}{\log}</math> שואף לאינסוף באופן רציף, ולכן הטנגנס עושה אינסוף מחזורים ולכן לא קיים הגבול החד־צדדי ולכן אלה נקודות אי־רציפות מ'''מין שני'''. | |
| − | במקומות בהם <math>\ | + | במקומות בהם <math>\frac{1}{\log(x^2)}=\frac{\pi}{2}+\pi k</math> הטנגנס לא מוגדר ושואף לאינסוף ולכן אלו נקודות אי־רציפות מ'''מין שני'''. נקודות אלה הן מהצורה <math>\sqrt{e^\frac{1}{\frac{\pi}{2}+\pi k}}</math> |
==שאלה 5== | ==שאלה 5== | ||
| שורה 66: | שורה 66: | ||
===א=== | ===א=== | ||
| − | <math>e^{-|\tan(x)|}</math> בקטע <math>\left(-\ | + | <math>e^{-|\tan(x)|}</math> בקטע <math>\left(-\tfrac{\pi}{2},\tfrac{\pi}{2}\right)</math> |
הפונקציה רציפה בכל הקטע ובקצות הקטע <math>|\tan(x)|\to\infty</math> ולכן סה"כ הגבולות הם <math>0</math> כלומר סופיים ולכן הפונקציה '''רציפה במ"ש'''. | הפונקציה רציפה בכל הקטע ובקצות הקטע <math>|\tan(x)|\to\infty</math> ולכן סה"כ הגבולות הם <math>0</math> כלומר סופיים ולכן הפונקציה '''רציפה במ"ש'''. | ||
| שורה 73: | שורה 73: | ||
<math>\log\big(2+\cos(x)\big)</math> בכל הממשיים. | <math>\log\big(2+\cos(x)\big)</math> בכל הממשיים. | ||
| − | <math>2+\cos(x)</math> רציפה במ"ש בכל הממשיים, ומקבלת ערכים בקטע <math>[1,3]</math>. בקטע הזו <math>\log</math> רציפה במ"ש ולכן סה"כ יש לנו הרכבה של רציפות במ"ש ולכן הפונקציה '''רציפה במ"ש'''. | + | <math>2+\cos(x)</math> רציפה במ"ש בכל הממשיים, ומקבלת ערכים בקטע <math>[1,3]</math> . בקטע הזו <math>\log</math> רציפה במ"ש ולכן סה"כ יש לנו הרכבה של רציפות במ"ש ולכן הפונקציה '''רציפה במ"ש'''. |
===ג=== | ===ג=== | ||
<math>\cos\big(\log(x)\big)</math> בקטע <math>(0,\infty)</math> | <math>\cos\big(\log(x)\big)</math> בקטע <math>(0,\infty)</math> | ||
| − | ניקח שתי סדרות ששואפות | + | ניקח שתי סדרות ששואפות ל־<math>0</math> , אבל הפונקציה עליהן תהיה קבועה. על האחת <math>1</math> ועל השניה <math>-1</math>, וזה יסתור רציפות במ"ש. <math>y_n=e^{-2\pi n-\pi}</math>, <math>x_n=e^{-2\pi n}</math> |
==שאלה 6== | ==שאלה 6== | ||
| שורה 89: | שורה 89: | ||
הוכח שאם קיים הגבול <math>\lim\limits_{x\to x_0}f'(x)=L</math> אזי מתקיים <math>f'(x_0)=L</math> . | הוכח שאם קיים הגבול <math>\lim\limits_{x\to x_0}f'(x)=L</math> אזי מתקיים <math>f'(x_0)=L</math> . | ||
| − | לפי הגדרה <math>f'(x_0)=\lim\limits_{x\to x_0}\ | + | לפי הגדרה <math>f'(x_0)=\lim\limits_{x\to x_0}\dfrac{f(x)-f(x_0)}{x-x_0}</math> . ברור כי <math>\lim\limits_{x\to x_0}(x-x_0)=0</math> ומכיון ש־ <math>f</math> רציפה אזי גם <math>\lim\limits_{x\to x_0}\big[f(x)-f(x_0)\big]=0</math> . לכן אם יש גבול לנגזרת של המונה חלקי הנגזרת של המכנה אז הוא שווה לגבול המקורי לפי לופיטל. |
נגזור את המונה והמכנה לקבל <math>\frac{f'(x)}{1}\to L</math> ולכן קיבלנו את מה שרצינו. | נגזור את המונה והמכנה לקבל <math>\frac{f'(x)}{1}\to L</math> ולכן קיבלנו את מה שרצינו. | ||
| שורה 96: | שורה 96: | ||
מצא פונקציה כנ"ל כך שלא קיים הגבול <math>\lim\limits_{x\to x_0}f'(x)</math> | מצא פונקציה כנ"ל כך שלא קיים הגבול <math>\lim\limits_{x\to x_0}f'(x)</math> | ||
| − | כפי שראינו בכיתה, נשתמש בפונקציה <math>f(x)=x^2 | + | כפי שראינו בכיתה, נשתמש בפונקציה <math>f(x)=\begin{cases}x^2\sin\left(\frac1x\right)&:x\ne0\\0&:x=0\end{cases}</math> . ברור שהיא גזירה בכל מקום פרט ל־ <math>0</math> , נוכיח שהיא גם גזירה ב־<math>0</math> . |
| + | :<math>f'(0)=\lim\limits_{x\to0}\dfrac{f(x)-f(0)}{x-0}=\lim\limits_{x\to 0}x\sin\left(\frac1x\right)=0</math> | ||
| + | לכן ערך הנגזרת ב־<math>0</math> הוא <math>0</math> . מהו גבול הנגזרת ב־<math>x_0=0</math>? | ||
| − | + | הנגזרת בנקודות השונות מאפס שווה ל־<math>2x\sin\left(\frac1x\right)-\cos\left(\frac1x\right)</math> . לכן גבולה ב־<math>0</math> לא קיים (<math>0</math> ועוד משהו לא קיים) כפי שרצינו. | |
| − | + | ||
| − | הנגזרת בנקודות השונות מאפס שווה | + | |
==שאלה 8== | ==שאלה 8== | ||
| − | תהי פונקציה גזירה ורציפה במ"ש | + | תהי פונקציה גזירה ורציפה במ"ש ב־<math>(-1,1)</math> . הוכח/הפרך: <math>f'</math> חסומה על כל תת־קטע סגור של <math>(-1,1)</math> . |
===הפרכה=== | ===הפרכה=== | ||
| − | למעשה אנו '''חייבים''' נגזרת שאינה רציפה כמו בשאלה 7 סעיף ב', אחרת פונקציה רציפה על קטע סגור חסומה בו. נביט בפונקציה <math>f(x)=x^2 | + | למעשה אנו '''חייבים''' נגזרת שאינה רציפה כמו בשאלה 7 סעיף ב', אחרת פונקציה רציפה על קטע סגור חסומה בו. נביט בפונקציה |
| + | :<math>f(x)=\begin{cases}x^2\sin\left(\frac{1}{x^2}\right)&:x\ne0\\0&:x=0\end{cases}</math> | ||
| + | היא גזירה כמו שראינו בשאלה קודמת. הנגזרת הנה <math>2x\sin\left(\frac{1}{x^2}\right)-\frac2x\cos\left(\frac{1}{x^2}\right)</math> . נביט בסדרה השואפת לאפס <math>x_n=\frac{1}{\sqrt{2\pi n}}</math> עליה מקבלים <math>f'(x_n)=-2\sqrt{2\pi n}\to-\infty</math> ולכן הנגזרת אינה חסומה בקטע הסגור <math>[-0.5,0.5]</math> . | ||
גרסה אחרונה מ־11:59, 29 באוגוסט 2018
תוכן עניינים
המבחן של פרופ' זלצמן
שאלה 1
תהי סדרה  , ותהי
, ותהי  קבוצות הגבולות החלקיים שלה. הוכח/הפרך:
קבוצות הגבולות החלקיים שלה. הוכח/הפרך:  סגורה
סגורה
הוכחה
על־מנת להוכיח כי  סגורה, יש להוכיח שהיא מכילה את כל נקודות ההצטברות שלה. כלומר, אם
סגורה, יש להוכיח שהיא מכילה את כל נקודות ההצטברות שלה. כלומר, אם 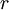 היא נקודת הצטברות של
היא נקודת הצטברות של  אזי היא גם גבול חלקי של
אזי היא גם גבול חלקי של  .
.
נניח 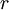 נקודת הצטברות של
נקודת הצטברות של  , לכן לכל
, לכן לכל  קיים גבול חלקי הקרוב ל־
קיים גבול חלקי הקרוב ל־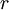 עד כדי
עד כדי  , ולכל גבול חלקי כזה קיימת תת-סדרה המתכנסת אליו.
, ולכל גבול חלקי כזה קיימת תת-סדרה המתכנסת אליו.
לכן, עבור  קיימת תת-סדרה המתכנסת למספר הקרוב ל־
קיימת תת-סדרה המתכנסת למספר הקרוב ל־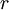 עד כדי
עד כדי  . לכן קיים בסדרה הזו מקום אשר החל ממנו והלאה כל האיברים קרובים ל־
. לכן קיים בסדרה הזו מקום אשר החל ממנו והלאה כל האיברים קרובים ל־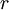 עד כדי
עד כדי  (המרחק בין גבול תת־הסדרה לבין
(המרחק בין גבול תת־הסדרה לבין 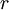 ועוד מרחק בין איברי תת־הסדרה לגבול תת־הסדרה). נבחר איברים כאלה מתת־הסדרות, ובלבד שכל איבר יהיה אחרי האיבר הקודם. כך בנינו סדרה שאיבריה קרובים מרחק
ועוד מרחק בין איברי תת־הסדרה לגבול תת־הסדרה). נבחר איברים כאלה מתת־הסדרות, ובלבד שכל איבר יהיה אחרי האיבר הקודם. כך בנינו סדרה שאיבריה קרובים מרחק  מ־
מ־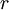 ולכן היא ודאי מתכנסת ל־
ולכן היא ודאי מתכנסת ל־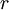 כפי שרצינו.
כפי שרצינו. 
שאלה 2
בדוק התכנסות של הטורים הבאים:
א
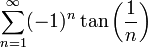
נבדוק התכנסות בהחלט, נוכיח שהטור חבר של הטור ההרמוני:
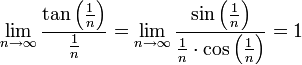
ולכן הוא אינו מתכנס בהחלט.
קל לראות כי 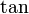 מונוטונית באזור
מונוטונית באזור  (נגזרתה חיובית בלבד), וכמו כן
(נגזרתה חיובית בלבד), וכמו כן 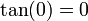 והיא רציפה שם ולכן סה"כ יש לנו סדרה המתכנסת מונוטונית ל־
והיא רציפה שם ולכן סה"כ יש לנו סדרה המתכנסת מונוטונית ל־ ולפי משפט לייבניץ הטור כולו מתכנס בתנאי.
ולפי משפט לייבניץ הטור כולו מתכנס בתנאי.
ב
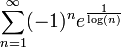
קל לראות כי 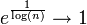 ולכן הטור מתבדר.
ולכן הטור מתבדר.
ג
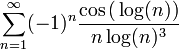
בערך מוחלט זה קטן מ־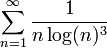 . זו סדרה מונוטונית יורדת ולכן ניתן להפעיל את מבחן העיבוי לקבל את הטור
. זו סדרה מונוטונית יורדת ולכן ניתן להפעיל את מבחן העיבוי לקבל את הטור
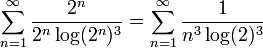 שהוא כמובן מתכנס, ולכן כל הטור מתכנס בהחלט.
שהוא כמובן מתכנס, ולכן כל הטור מתכנס בהחלט.
שאלה 3
ציטוט משפטים – תשובות במחברת ההרצאה
שאלה 4
זהה וסווג נקודות אי־רציפות:
א
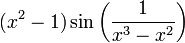
נקודות אי־הרציפות הן כאשר המכנה מתאפס, כלומר 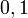 . ב־
. ב־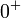 ,
, 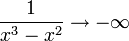 . מכיון שזו פונקציה רציפה ששואפת לאינסוף, הסינוס מקבל עליה אינסוף מחזורים ולכן אין לו גבול.
. מכיון שזו פונקציה רציפה ששואפת לאינסוף, הסינוס מקבל עליה אינסוף מחזורים ולכן אין לו גבול. 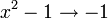 ולכן סה"כ יש לנו פונקציה עם גבול סופי שונה מ־
ולכן סה"כ יש לנו פונקציה עם גבול סופי שונה מ־ גבול פונקציה ללא גבול ולכן לא קיים הגבול החד־צדדי ולכן נקודת אי־הרציפות
גבול פונקציה ללא גבול ולכן לא קיים הגבול החד־צדדי ולכן נקודת אי־הרציפות  הנה ממין שני.
הנה ממין שני.
בנקודה 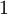 אנחנו מקבלים פונקציה ששואפת ל־
אנחנו מקבלים פונקציה ששואפת ל־ כפול חסומה' ולכן סה"כ יש שאיפה ל־
כפול חסומה' ולכן סה"כ יש שאיפה ל־ וזו נקודת אי־רציפות סליקה.
וזו נקודת אי־רציפות סליקה.
ב
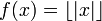
נניח ש[x] הוא המספר השלם הגדול ביותר שקטן או שווה ל־ . אזי עבור
. אזי עבור 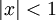 מתקיים
מתקיים 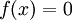 ולכן שם הפונקציה רציפה. עבור
ולכן שם הפונקציה רציפה. עבור 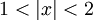 מתקיים
מתקיים 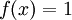 ולכן
ולכן 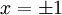 הנן נקודות אי־רציפות ממין ראשון (הגבול הוא
הנן נקודות אי־רציפות ממין ראשון (הגבול הוא 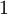 מצד אחד ו־
מצד אחד ו־ מהצד השני). באופן דומה לכל
מהצד השני). באופן דומה לכל  טבעי מתקיים ש
טבעי מתקיים ש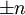 הן נקודות אי-רציפות ממין ראשון.
הן נקודות אי-רציפות ממין ראשון.
ג
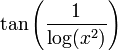
ב־ , הלוגריתם שואף ל־
, הלוגריתם שואף ל־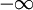 ולכן
ולכן 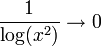 ולכן הגבול כולו הוא
ולכן הגבול כולו הוא  וזו נקודת אי־רציפות סליקה.
וזו נקודת אי־רציפות סליקה.
ב־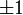 הלוגריתם שואף ל־
הלוגריתם שואף ל־ ולכן מצד אחד
ולכן מצד אחד 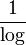 שואף לאינסוף באופן רציף, ולכן הטנגנס עושה אינסוף מחזורים ולכן לא קיים הגבול החד־צדדי ולכן אלה נקודות אי־רציפות ממין שני.
שואף לאינסוף באופן רציף, ולכן הטנגנס עושה אינסוף מחזורים ולכן לא קיים הגבול החד־צדדי ולכן אלה נקודות אי־רציפות ממין שני.
במקומות בהם 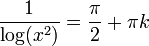 הטנגנס לא מוגדר ושואף לאינסוף ולכן אלו נקודות אי־רציפות ממין שני. נקודות אלה הן מהצורה
הטנגנס לא מוגדר ושואף לאינסוף ולכן אלו נקודות אי־רציפות ממין שני. נקודות אלה הן מהצורה 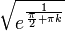
שאלה 5
האם הפונקציות הבאות רציפות במ"ש בקטעים הנתונים?
א
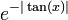 בקטע
בקטע 
הפונקציה רציפה בכל הקטע ובקצות הקטע 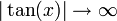 ולכן סה"כ הגבולות הם
ולכן סה"כ הגבולות הם  כלומר סופיים ולכן הפונקציה רציפה במ"ש.
כלומר סופיים ולכן הפונקציה רציפה במ"ש.
ב
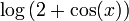 בכל הממשיים.
בכל הממשיים.
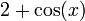 רציפה במ"ש בכל הממשיים, ומקבלת ערכים בקטע
רציפה במ"ש בכל הממשיים, ומקבלת ערכים בקטע ![[1,3]](/images/math/6/8/9/689e1b934020b6eb3917c155d94a9a0f.png) . בקטע הזו
. בקטע הזו 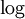 רציפה במ"ש ולכן סה"כ יש לנו הרכבה של רציפות במ"ש ולכן הפונקציה רציפה במ"ש.
רציפה במ"ש ולכן סה"כ יש לנו הרכבה של רציפות במ"ש ולכן הפונקציה רציפה במ"ש.
ג
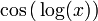 בקטע
בקטע 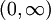
ניקח שתי סדרות ששואפות ל־ , אבל הפונקציה עליהן תהיה קבועה. על האחת
, אבל הפונקציה עליהן תהיה קבועה. על האחת 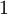 ועל השניה
ועל השניה 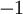 , וזה יסתור רציפות במ"ש.
, וזה יסתור רציפות במ"ש. 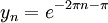 ,
, 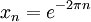
שאלה 6
נגזרות
שאלה 7
תהי  גזירה בקטע
גזירה בקטע 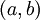 ותהי נקודה
ותהי נקודה 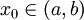
א
הוכח שאם קיים הגבול 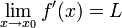 אזי מתקיים
אזי מתקיים 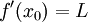 .
.
לפי הגדרה 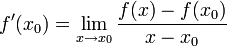 . ברור כי
. ברור כי 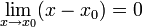 ומכיון ש־
ומכיון ש־  רציפה אזי גם
רציפה אזי גם ![\lim\limits_{x\to x_0}\big[f(x)-f(x_0)\big]=0](/images/math/e/8/b/e8be112d40e5964c98c4e6f153fe95c2.png) . לכן אם יש גבול לנגזרת של המונה חלקי הנגזרת של המכנה אז הוא שווה לגבול המקורי לפי לופיטל.
. לכן אם יש גבול לנגזרת של המונה חלקי הנגזרת של המכנה אז הוא שווה לגבול המקורי לפי לופיטל.
נגזור את המונה והמכנה לקבל 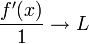 ולכן קיבלנו את מה שרצינו.
ולכן קיבלנו את מה שרצינו.
ב
מצא פונקציה כנ"ל כך שלא קיים הגבול 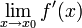
כפי שראינו בכיתה, נשתמש בפונקציה 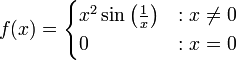 . ברור שהיא גזירה בכל מקום פרט ל־
. ברור שהיא גזירה בכל מקום פרט ל־  , נוכיח שהיא גם גזירה ב־
, נוכיח שהיא גם גזירה ב־ .
.
לכן ערך הנגזרת ב־ הוא
הוא  . מהו גבול הנגזרת ב־
. מהו גבול הנגזרת ב־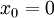 ?
?
הנגזרת בנקודות השונות מאפס שווה ל־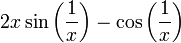 . לכן גבולה ב־
. לכן גבולה ב־ לא קיים (
לא קיים ( ועוד משהו לא קיים) כפי שרצינו.
ועוד משהו לא קיים) כפי שרצינו.
שאלה 8
תהי פונקציה גזירה ורציפה במ"ש ב־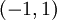 . הוכח/הפרך:
. הוכח/הפרך: 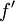 חסומה על כל תת־קטע סגור של
חסומה על כל תת־קטע סגור של 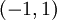 .
.
הפרכה
למעשה אנו חייבים נגזרת שאינה רציפה כמו בשאלה 7 סעיף ב', אחרת פונקציה רציפה על קטע סגור חסומה בו. נביט בפונקציה
היא גזירה כמו שראינו בשאלה קודמת. הנגזרת הנה 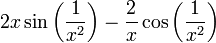 . נביט בסדרה השואפת לאפס
. נביט בסדרה השואפת לאפס 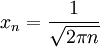 עליה מקבלים
עליה מקבלים 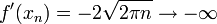 ולכן הנגזרת אינה חסומה בקטע הסגור
ולכן הנגזרת אינה חסומה בקטע הסגור ![[-0.5,0.5]](/images/math/1/f/b/1fb71d2ad3030bb1db7685d282418ba0.png) .
.