88-133 אינפי 2 תשעב סמסטר ב/הרצאה 5 (18/3/12)
מתוך Math-Wiki
הרצאות 5+6+7 (18+20+25/3/12)
הפעם אין צורך שאני יעלה את ההרצאות במלואן כי מצאתי את החומר באתר, אבל בשביל הנוחות אתן קישורים:
חלקים 1-3 : האינטגרל לפי דרבו
חלק 3 חלקים 3-4 : האינטגרל לפי רימן
משפט 1: יהיו 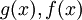 מוגדרות ואינטגרביליות ב-
מוגדרות ואינטגרביליות ב- ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ו-
ו- 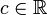 קבוע. אז הפונקציות
קבוע. אז הפונקציות 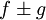 אינטגרביליות ב-
אינטגרביליות ב- ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ומתקיים:
ומתקיים:
1) ![\int_{a}^{b}\left [ f(x) \pm g(x) \right ]dx=\int_{a}^{b}f(x)dx \pm \int_{a}^{b}g(x)dx](/images/math/8/8/e/88e87439c10a8ef79cb26fe654f642f5.png)
2) 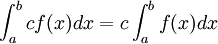
3) אם 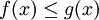 אז
אז 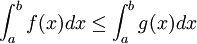
4) 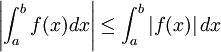
5) אם 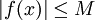 ב-
ב- ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) מתקיים:
מתקיים: 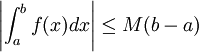
6) 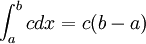
משפט 2 (המשפט היסודי של החשבון האינטגרלי- משפט ניוטון-לייבניץ):
תהי  מוגדרת חסימה ואינטגרבילית בקטע
מוגדרת חסימה ואינטגרבילית בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . נגדיר:
. נגדיר:
![\forall x \in [a,b]: A(x):= \int_{a}^{x} f(t)dt](/images/math/d/5/c/d5cdf40dff23af50b5e4a2ddc27970b2.png) .אזי:
.אזי:
א) 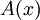 רציפה ב-
רציפה ב- ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
ב) אם 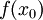 רציפה עבור
רציפה עבור 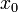 , אזי
, אזי 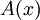 גזירה שם ומתקיים
גזירה שם ומתקיים 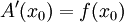 .
.
ג) אם  רציפה בכל
רציפה בכל ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , ו-F פונקציה קדומה ל-f,אז מתקיימת נוסחת ניוטון לייבניץ:
, ו-F פונקציה קדומה ל-f,אז מתקיימת נוסחת ניוטון לייבניץ: 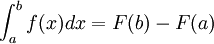 .
.
משפט 3 אינטגרל מסויים בחלקים:
![\int_{a}^{b} f(x)g'(x)dx=[f(x)g(x)]_{a}^{b}-\int_{a}^{b} f'(x)g(x)dx](/images/math/5/4/4/5449516b6463fbbc5e5976872840f487.png)
את ההוכחות אני יעלה במועד מאוחר יותר!
למקרה שיש טעות או שחסר חומר, תוכלו לפנות אליי דרך פייסבוק (שם המשתמש: Nimrod Sherer)