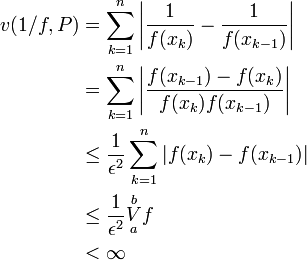הבדלים בין גרסאות בדף "88-133 אינפי 2 תשעב סמסטר ב/פתרון מועד א"
(←6 במבחן של שיין והורוביץ) |
יהודה שמחה (שיחה | תרומות) מ |
||
| שורה 5: | שורה 5: | ||
חשבו את האינטגרלים הבאים: | חשבו את האינטגרלים הבאים: | ||
===א=== | ===א=== | ||
| − | <math>\int\frac{dx}{sin(x)}</math> | + | <math>\int\frac{dx}{\sin(x)}</math> |
'''פתרון''': | '''פתרון''': | ||
| − | נבצע [[מדיה:09Infi2Universal.pdf|הצבה אוניברסאלית]] <math>t=tan(\frac{x}{2})</math> לקבל | + | נבצע [[מדיה:09Infi2Universal.pdf|הצבה אוניברסאלית]] <math>t=\tan(\frac{x}{2})</math> לקבל |
| − | <math>\int\frac{1+t^2}{2t}\frac{2}{1+t^2}dt=ln|t|+c</math> | + | <math>\int\frac{1+t^2}{2t}\cdot\frac{2}{1+t^2}dt=\ln\bigl(|t|\bigr)+c</math> |
===ב=== | ===ב=== | ||
| − | <math>\int\frac{ | + | <math>\int\frac{x\cdot dx}{\cos^2(x)}</math> |
נבצע [[אינטגרציה בחלקים]] לקבל | נבצע [[אינטגרציה בחלקים]] לקבל | ||
| − | <math>\int\frac{ | + | <math>\int\frac{x\cdot dx}{\cos^2(x)}=x\cdot\tan(x)-\int \tan(x) = x\cdot\tan(x)+\ln\bigl(|\cos(x)|\bigr)+c</math> |
===ג=== | ===ג=== | ||
<math>\int\frac{t^7}{1+2t^4+t^8}dt</math> | <math>\int\frac{t^7}{1+2t^4+t^8}dt</math> | ||
| − | ניתן לבצע את ה[[אלגוריתם לביצוע אינטגרל על פונקציה רציונאלית]] | + | ניתן לבצע את ה[[אלגוריתם לביצוע אינטגרל על פונקציה רציונאלית]] |
או ההצבה <math>x=t^4</math> באופן הבא: | או ההצבה <math>x=t^4</math> באופן הבא: | ||
| − | <math>\int \frac{t^7}{1+2t^4+t^8}dt=\int\frac{x}{4(1+2x+x^2)}dx=\ | + | <math>\int \frac{t^7}{1+2t^4+t^8}dt=\int\frac{x}{4(1+2x+x^2)}dx=\frac18\int\frac{2x+2-2}{(1+x)^2}dx=\frac{\ln(1+x)}{4}+\frac1{4(1+x)}+C</math> |
==3== | ==3== | ||
| שורה 37: | שורה 37: | ||
קבעו האם האינטגרל הבא מתכנס או מתבדר: | קבעו האם האינטגרל הבא מתכנס או מתבדר: | ||
| − | <math>\ | + | <math>\int\limits_0^\infty\frac{\arctan(x)}{x}dx</math> |
| − | + | ||
'''פתרון''': | '''פתרון''': | ||
| − | + | כיון ש- <math>\lim\limits_{x\to\infty}\frac{\frac{\arctan(x)}{x}}{\frac1{x}}=\frac{\pi}{2}</math> | |
| − | + | וכיון ש- <math>\displaystyle\int\limits_1^\infty\frac1{x}dx</math> מתבדר | |
שני האינטגרלים חברים ומתבדרים יחדיו. | שני האינטגרלים חברים ומתבדרים יחדיו. | ||
| − | |||
===ב=== | ===ב=== | ||
| − | הוכיחו שאם <math>p(x)</math> פולינום שאינו שווה זהותית | + | הוכיחו שאם <math>p(x)</math> פולינום שאינו שווה זהותית ל- <math>0</math>, אזי האינטגרל <math>\displaystyle\int\limits_1^\infty p(x)dx</math> מתבדר. |
| − | + | ||
'''פתרון''': | '''פתרון''': | ||
| − | אם הפולינום אינו זהותית | + | אם הפולינום אינו זהותית <math>0</math> , האינטגרל הלא-מסוים שלו <math>q(x)=\displaystyle\int\limits p(x)dx</math> בעל מעלה גדולה או שווה לאחד. ולכן |
| − | <math>\int_1^\infty p(x)dx=\lim_{b\ | + | <math>\int_1^\infty p(x)dx=\lim_{b\to\infty}\int_1^b p(x)dx=\lim_{b\to\infty}[q(b)-q(1)]=\pm\infty</math> |
| − | + | האחרון מתבדר כיון שהמעלה של <math>q</math> גדולה או שווה ל- <math>1</math> . | |
| − | האחרון מתבדר | + | |
==4== | ==4== | ||
| − | מצאו את טור | + | מצאו את טור מקלורן של הפונקציה <math>f(x)=\cos^2(x)</math> וקבעו את רדיוס ההתכנסות של הטור. |
| − | + | ||
'''פתרון''': | '''פתרון''': | ||
| − | ראשית, נשים לב כי <math>cos^2(x)= \frac{cos(2x)+1}{2}</math>. | + | ראשית, נשים לב כי <math>\cos^2(x)= \frac{\cos(2x)+1}{2}</math>. |
| − | שנית, נזכר או נפתח את הטור <math>\cos x = \ | + | שנית, נזכר או נפתח את הטור <math>\cos(x) = \sum_{n=0}^{\infty}\frac{(-1)^n}{(2n)!} x^{2n}</math> |
וביחד נקבל | וביחד נקבל | ||
| − | <math>cos^2(x)=\ | + | <math>\cos^2(x)=\frac12\bigg(\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n)!}(2x)^{2n}+1\bigg)=\frac12\bigg(1+\sum_{n=0}^{\infty}\frac{(-4)^n}{(2n)!}x^{2n}\bigg)</math> |
| − | \ | + | |
| − | + | ||
| − | </math> | + | |
קל לחשב רדיוס התכנסות של טור זה ולהראות שהוא אינסוף. | קל לחשב רדיוס התכנסות של טור זה ולהראות שהוא אינסוף. | ||
| שורה 84: | שורה 76: | ||
===א=== | ===א=== | ||
| − | קבעו אם הסדרה מתכנסת במ"ש בקטע <math>[0,\ | + | קבעו אם הסדרה מתכנסת במ"ש בקטע <math>\left[0,\frac12\right]</math> |
| − | + | ||
'''פתרון''': | '''פתרון''': | ||
| − | קל לראות שבקטע זה גבול הסדרה הוא הפונקציה ששווה זהותית | + | קל לראות שבקטע זה גבול הסדרה הוא הפונקציה ששווה זהותית <math>0</math> , ולכן יש לחשב את הגבול: |
| + | <math>\lim\limits_{n\to\infty}\Big[\sup_{x\in [0,\frac12]}\bigg|\frac{x^n}{1+x^n}\bigg|\Big]</math> | ||
| − | + | נגזור על-מנת למצוא את המקסימום: | |
| + | <math>{\Big(\frac{x^n}{1+x^n}\Big)' = \frac{nx^{n-1}(1+x^n)-nx^{n-1}\cdot x^n}{(1+x^n)^2}=\frac{nx^{n-1}}{(1+x^n)^2}}</math> | ||
| − | + | הנגזרת מתאפסת ב- <math>0</math> , לכן המקסימום הוא בקצוות | |
| + | <math>f_n(0)=0</math> , | ||
| − | <math> | + | <math>f_n(\frac12)=\frac1{2^n+1}</math> |
| + | ולכן | ||
| − | + | <math>\lim\limits_{n\to\infty}\Big[\sup_{x\in [0,\frac12]}\bigg|\frac{x^n}{1+x^n}\bigg|\Big]= \lim\limits_{n\to\infty}\frac1{2^n+1}=0</math> | |
| − | + | ||
| − | + | ||
| − | <math> | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
ולכן הסדרה '''מתכנסת במ"ש'''. | ולכן הסדרה '''מתכנסת במ"ש'''. | ||
===ב=== | ===ב=== | ||
| − | קבעו אם הסדרה מתכנסת במ"ש בקטע <math>[\ | + | קבעו אם הסדרה מתכנסת במ"ש בקטע <math>\left[\frac12,\frac32\right]</math> |
| − | + | ||
'''פתרון''': | '''פתרון''': | ||
| − | קל לראות כי פונקצית הגבול בנקודה 1 היא | + | קל לראות כי פונקצית הגבול בנקודה <math>1</math> היא <math>\frac12</math> , לכל נקודה גדולה מ- <math>1</math> היא <math>1</math> ולכל נקודה קטנה מ- <math>1</math> היא <math>0</math> . לכן פונקצית הגבול אינה רציפה, ולכן ההתכנסות אינה במ"ש (שכן התכנסות במ"ש של פונקציות רציפות היא רציפה). |
==6 במבחן של אגרונובסקי== | ==6 במבחן של אגרונובסקי== | ||
| − | הוכח כי הפונקציה <math>F(\alpha)=\ | + | הוכח כי הפונקציה <math>F(\alpha)=\displaystyle\int\limits_1^\infty x^\alpha e^{-x}dx</math> רציפה בכל הממשיים. |
| − | + | ||
'''פתרון''': | '''פתרון''': | ||
| − | *לפי מבחן השוואה גבולי, קל לראות | + | *לפי מבחן השוואה גבולי, קל לראות שכיון שהאינטגרל <math>\displaystyle\int\limits_1^\infty e^{-\frac{x}{2}}dx</math> מתכנס, כך גם האינטגרל <math>F(\alpha)</math> לכל אלפא. |
| − | *כמו כן קל לוודא כי הפונקציה <math>F(\alpha)</math> מונוטונית. (זה לבד מוכיח רציפות פרט למספר בן | + | *כמו כן קל לוודא כי הפונקציה <math>F(\alpha)</math> מונוטונית. (זה לבד מוכיח רציפות פרט למספר בן-מניה של נקודות...) |
| − | *תהי | + | *תהי <math>a</math> נקודה מסוימת. נבחר <math>M</math> כך ש- <math>\displaystyle\int\limits_M^\infty x^{a+1}e^{-x}dx < \frac{\epsilon}{2}</math> |
| − | + | ||
| − | + | ||
| + | *כעת עבור <math>\Delta a</math> קטן מספיק, <math>F(a+\Delta a)\le \displaystyle\int\limits_1^Mx^{a+\Delta a}e^{-x}dx + \frac{\epsilon}{2}\le M^{\Delta a}F(a) + \frac{\epsilon}{2}\le F(a) + \epsilon</math> | ||
כפי שרצינו... | כפי שרצינו... | ||
| שורה 146: | שורה 125: | ||
==6 במבחן של שיין והורוביץ== | ==6 במבחן של שיין והורוביץ== | ||
(לקוח ממערכי התרגול של אור שחף) | (לקוח ממערכי התרגול של אור שחף) | ||
| − | נתונה f פונקציה בעלת השתנות חסומה בקטע, ונתון שקיים <math>\ | + | נתונה f פונקציה בעלת השתנות חסומה בקטע, ונתון שקיים <math>\epsilon>0</math> כך ש-<math>f(x)\ge\epsilon</math> לכל <math>x\in[a,b]</math>. הוכיחו <math>\frac1f</math> בעלת השתנות חסומה בקטע. |
===פתרון=== | ===פתרון=== | ||
| − | # מתקיים <math>\forall x\in[a,b]:\ \frac1{f(x)}\le\frac1\ | + | # מתקיים <math>\forall x\in[a,b]:\ \frac1{f(x)}\le\frac1\epsilon</math> ולכן |
| + | <math> | ||
| + | \begin{align}v(1/f,P)&=\sum_{k=1}^n\left|\frac1{f(x_k)}-\frac1{f(x_{k-1})}\right|\\&=\sum_{k=1}^n\left|\frac{f(x_{k-1})-f(x_k)}{f(x_k)f(x_{k-1})}\right|\\&\le\frac1{\epsilon^2}\sum_{k=1}^n|f(x_k)-f(x_{k-1})|\\&\le\frac1{\epsilon^2}\overset b\underset aV f\\&<\infty\end{align} | ||
| + | </math> | ||
[[קטגוריה:אינפי]] | [[קטגוריה:אינפי]] | ||
גרסה אחרונה מ־17:49, 1 בפברואר 2016
תוכן עניינים
1
שאלת הוכחה מההרצאה
2
חשבו את האינטגרלים הבאים:
א
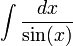
פתרון:
נבצע הצבה אוניברסאלית 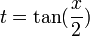 לקבל
לקבל
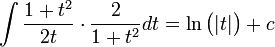
ב
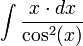
נבצע אינטגרציה בחלקים לקבל
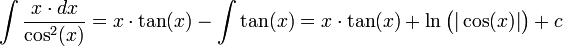
ג
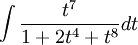
ניתן לבצע את האלגוריתם לביצוע אינטגרל על פונקציה רציונאלית
או ההצבה 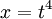 באופן הבא:
באופן הבא:
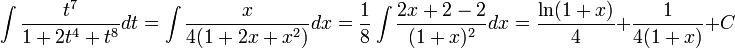
3
א
קבעו האם האינטגרל הבא מתכנס או מתבדר:
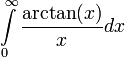
פתרון:
כיון ש- 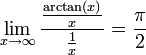
וכיון ש- 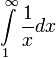 מתבדר
מתבדר
שני האינטגרלים חברים ומתבדרים יחדיו.
ב
הוכיחו שאם 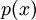 פולינום שאינו שווה זהותית ל-
פולינום שאינו שווה זהותית ל-  , אזי האינטגרל
, אזי האינטגרל 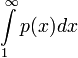 מתבדר.
מתבדר.
פתרון:
אם הפולינום אינו זהותית  , האינטגרל הלא-מסוים שלו
, האינטגרל הלא-מסוים שלו 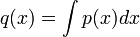 בעל מעלה גדולה או שווה לאחד. ולכן
בעל מעלה גדולה או שווה לאחד. ולכן
![\int_1^\infty p(x)dx=\lim_{b\to\infty}\int_1^b p(x)dx=\lim_{b\to\infty}[q(b)-q(1)]=\pm\infty](/images/math/8/6/b/86b1834363cff307cc238670d807c007.png)
האחרון מתבדר כיון שהמעלה של 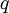 גדולה או שווה ל-
גדולה או שווה ל- 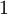 .
.
4
מצאו את טור מקלורן של הפונקציה 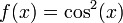 וקבעו את רדיוס ההתכנסות של הטור.
וקבעו את רדיוס ההתכנסות של הטור.
פתרון:
ראשית, נשים לב כי 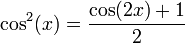 .
.
שנית, נזכר או נפתח את הטור 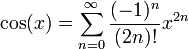
וביחד נקבל
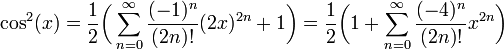
קל לחשב רדיוס התכנסות של טור זה ולהראות שהוא אינסוף.
5
נגדיר סדרת פונקציות 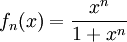
א
קבעו אם הסדרה מתכנסת במ"ש בקטע ![\left[0,\frac12\right]](/images/math/e/6/0/e6027e3d8b6bc012de5e93a08e736ea1.png)
פתרון:
קל לראות שבקטע זה גבול הסדרה הוא הפונקציה ששווה זהותית  , ולכן יש לחשב את הגבול:
, ולכן יש לחשב את הגבול:
![\lim\limits_{n\to\infty}\Big[\sup_{x\in [0,\frac12]}\bigg|\frac{x^n}{1+x^n}\bigg|\Big]](/images/math/9/8/c/98c61e292fa287096245ce11d51c3580.png)
נגזור על-מנת למצוא את המקסימום:
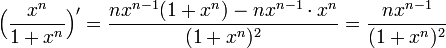
הנגזרת מתאפסת ב-  , לכן המקסימום הוא בקצוות
, לכן המקסימום הוא בקצוות
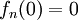 ,
,
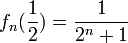
ולכן
![\lim\limits_{n\to\infty}\Big[\sup_{x\in [0,\frac12]}\bigg|\frac{x^n}{1+x^n}\bigg|\Big]= \lim\limits_{n\to\infty}\frac1{2^n+1}=0](/images/math/0/8/4/084f61bbbce990f3735bf3f080c66d59.png)
ולכן הסדרה מתכנסת במ"ש.
ב
קבעו אם הסדרה מתכנסת במ"ש בקטע ![\left[\frac12,\frac32\right]](/images/math/a/8/e/a8e41093351d25d81487004f55ef6c3d.png)
פתרון:
קל לראות כי פונקצית הגבול בנקודה 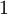 היא
היא  , לכל נקודה גדולה מ-
, לכל נקודה גדולה מ- 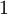 היא
היא 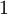 ולכל נקודה קטנה מ-
ולכל נקודה קטנה מ- 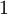 היא
היא  . לכן פונקצית הגבול אינה רציפה, ולכן ההתכנסות אינה במ"ש (שכן התכנסות במ"ש של פונקציות רציפות היא רציפה).
. לכן פונקצית הגבול אינה רציפה, ולכן ההתכנסות אינה במ"ש (שכן התכנסות במ"ש של פונקציות רציפות היא רציפה).
6 במבחן של אגרונובסקי
הוכח כי הפונקציה 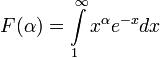 רציפה בכל הממשיים.
רציפה בכל הממשיים.
פתרון:
- לפי מבחן השוואה גבולי, קל לראות שכיון שהאינטגרל
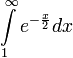 מתכנס, כך גם האינטגרל
מתכנס, כך גם האינטגרל 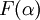 לכל אלפא.
לכל אלפא.
- כמו כן קל לוודא כי הפונקציה
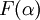 מונוטונית. (זה לבד מוכיח רציפות פרט למספר בן-מניה של נקודות...)
מונוטונית. (זה לבד מוכיח רציפות פרט למספר בן-מניה של נקודות...)
- תהי
 נקודה מסוימת. נבחר
נקודה מסוימת. נבחר 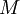 כך ש-
כך ש- 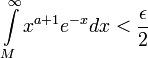
- כעת עבור
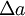 קטן מספיק,
קטן מספיק, 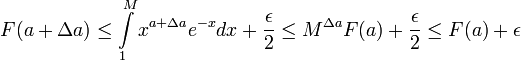
כפי שרצינו...
6 במבחן של שיין והורוביץ
(לקוח ממערכי התרגול של אור שחף)
נתונה f פונקציה בעלת השתנות חסומה בקטע, ונתון שקיים 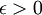 כך ש-
כך ש-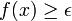 לכל
לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) . הוכיחו
. הוכיחו 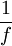 בעלת השתנות חסומה בקטע.
בעלת השתנות חסומה בקטע.
פתרון
- מתקיים
![\forall x\in[a,b]:\ \frac1{f(x)}\le\frac1\epsilon](/images/math/1/7/2/172da108ea4a1e9611da166f7fb91f20.png) ולכן
ולכן