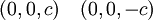שאלה 1
סעיף א
עבור נקודות 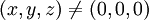 פשוט גוזרים את הפונקציה לפי
פשוט גוזרים את הפונקציה לפי 
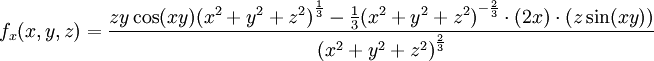
עבור הנקודה 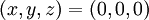 קל לראות ש
קל לראות ש
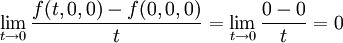
סעיף ב
כמו שראינו בקלות ש 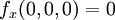 קל לראות שגם
קל לראות שגם 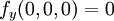 ו
ו 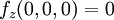 .
.
ראשית נוודא ש  רציפה (לא חייבים, אבל בדר"כ שווה לבדוק. כי אם היא לא רציפה אז ברור שהיא לא דיפרנציאבילית).
רציפה (לא חייבים, אבל בדר"כ שווה לבדוק. כי אם היא לא רציפה אז ברור שהיא לא דיפרנציאבילית).
נשים לב ש
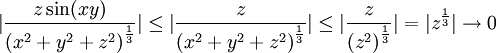
ולכן  רציפה.
רציפה.
נבדוק דיפרנציאביליות
צריך לבדוק אם 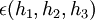 המוגדרת לפי:
המוגדרת לפי:
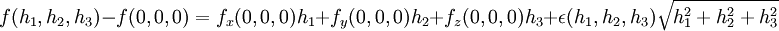
מתכנסת ל  בנקודה
בנקודה  .
.
במקרה שלנו צריך לבדוק את:
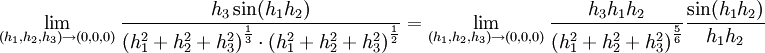
היות ו
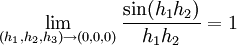
נותר לבדוק את
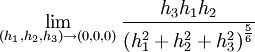
נשים לב ש
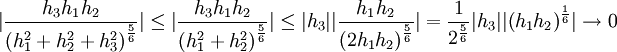
דרך אחרת (שימושית כאשר יש במכנה דברים בסגנון 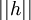 ):
):
עוברים לקוארדינטות כדוריות
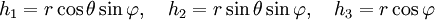
ואז צריך לחשב גבול
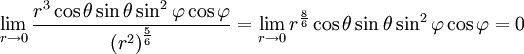
ולכן  דיפרנציאבילית ב
דיפרנציאבילית ב 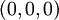 .
.
שאלה 3
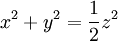
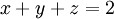
הנגזרות החלקיות של הפונקציות
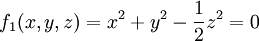
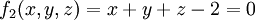
קיימות עד איזה סדר שרוצים.
כמו כן, הנקודה 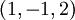 מקיימת את מערכת המשוואות.
מקיימת את מערכת המשוואות.
נבדוק את התנאי של משפט הפונקציה הסתומה
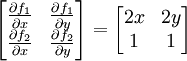
בנקודה 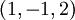 נקבל את המטריצה
נקבל את המטריצה
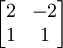
שהיא מטריצה הפיכה.
לכן לפי משפט הפונקציה הסתומה, אכן מוגדרות פונקציות של
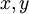 לפי
לפי 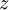
לפי משפט הפונקציה הסתומה, קיימת סביבה של הנקודה
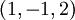 שבה מתקיים:
שבה מתקיים:
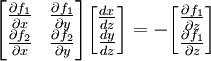
כלומר במקרה שלנו:
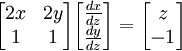
אם פותרים את המשוואות
רואים ש
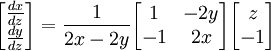
כלומר:
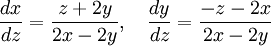
מכאן, על ידי הצבה של 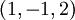 קל לראות שבנקודה
קל לראות שבנקודה 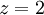 מתקיים
מתקיים
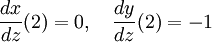
כמו כן נחשב את 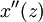 בסביבה של
בסביבה של 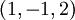 על ידי גזירה רגילה לפי
על ידי גזירה רגילה לפי 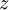 (אבל נשים לב ש
(אבל נשים לב ש 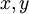 הם פונקציות של
הם פונקציות של 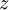 ):
):
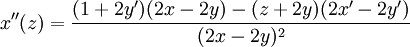
נציב 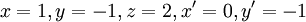 ונקבל:
ונקבל:
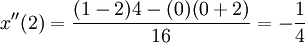
שאלה 4
סעיף א
המשוואות המדוברות דיפרנציאביליות ברציפות והגרדיאנט של התנאי הוא:
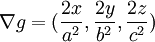
שהוא לא מתאפס בנקודות שמקיימות את התנאי.
לכן אפשר להשתמש בכופלי לגרנז ללא חשש.
שימוש בכופלי לגרנז מוביל אל המשוואות הבאות:
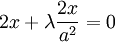
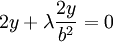
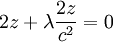
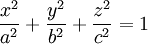
אם נסתכל על שלושת המשוואות הראשונות, נקבל מערכת משוואות לינארית
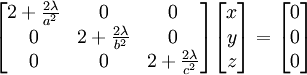
אם המטריצה הפיכה, אז הפתרון היחיד הוא
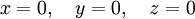
וזה לא יקיים את האילוץ
לכן בהכרח המטריצה לא הפיכה, כלומר
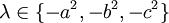
בגלל ש 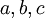 מספרים שונים אלה שלוש אפשרויות שונות.
מספרים שונים אלה שלוש אפשרויות שונות.
אם 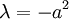 נקבל שבהכרח
נקבל שבהכרח 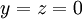 ולפי האילוץ
ולפי האילוץ
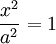 כלומר
כלומר 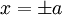 .
.
בדומה שתי האפשרויות האחרות הן:
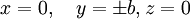
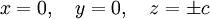
כעת נותר להחליט אם אלה אקסטרימלים (נקודות קיצון).
אפשר להפעיל שיקול כזה: היות ו  רציפה על קבוצה סגורה וחסומה, יש לה נקודות מינמום ומקסימום גלובאליות (שהן בפרט מקומיות).
ידוע שנקודות הקיצון המקומיות הן פתרונות של משוואות לגרנז'.
רציפה על קבוצה סגורה וחסומה, יש לה נקודות מינמום ומקסימום גלובאליות (שהן בפרט מקומיות).
ידוע שנקודות הקיצון המקומיות הן פתרונות של משוואות לגרנז'.
לכן שניים מהפתרונות חייבים להיות מינימום ומקסימום גלובאליים.
היות ו 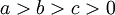 ברור ש
ברור ש
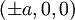 הן מקסימום גלובאלי.
הן מקסימום גלובאלי.
ו  הוא מינימום גלובאלי.
הוא מינימום גלובאלי.
כעת נותר להחליט האם 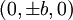 היא גם נקודת קיצון.
היא גם נקודת קיצון.
אפשר להפעיל שיקול כזה:
אם נסתכל על ההטלה על המישור 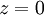 נקבל חישוב של
נקבל חישוב של 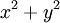 תחת האילוץ
תחת האילוץ 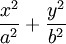
במצב כזה, 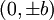 היא נקודת מינימום.
היא נקודת מינימום.
אם נסתכל על ההטלה למישור 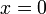 נקבל ש
נקבל ש 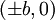 היא נקודת מקסימום.
היא נקודת מקסימום.
ולכן 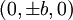 היא לא נקודת קיצון.
היא לא נקודת קיצון.
לסיכום נקודות הקיצון הן:
נקודות מקסימום
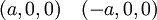
נקודות מינימום: