88-341 תשעג סמסטר א/יחידות ההצגה של שיטות ספירה מבוססות מיקום
נדון כאן בשאלה מתי למספר 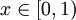 יש הצגה יחידה בפיתוח לפי בסיס
יש הצגה יחידה בפיתוח לפי בסיס 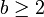 כלשהו (למשל בינארי או טרינארי). הקבוצה הרלוונטית לשאלה היא קבוצת הסדרות
כלשהו (למשל בינארי או טרינארי). הקבוצה הרלוונטית לשאלה היא קבוצת הסדרות 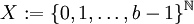 . והפונקציה הרלוונטית היא
. והפונקציה הרלוונטית היא 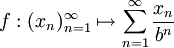
משפט
למספר 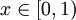 אין הצגה
אין הצגה 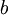 -ארית יחידה או"א ישנו
-ארית יחידה או"א ישנו 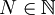 ומספר
ומספר 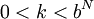 כך ש-
כך ש-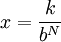 וגם
וגם 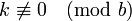
הוכחה
נניח כי 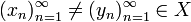 סדרות שונות של ספרות בבסיס
סדרות שונות של ספרות בבסיס 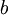 המייצגות את אותו מספר
המייצגות את אותו מספר  (ז"א
(ז"א 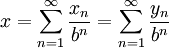 ).
).
יהי 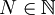 מיקומה של הספרה הראשונה בה הסדרות שונות זו מזו (ז"א
מיקומה של הספרה הראשונה בה הסדרות שונות זו מזו (ז"א 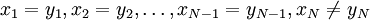 ) נניח בה"כ כי
) נניח בה"כ כי 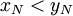 . אם כן:
. אם כן:
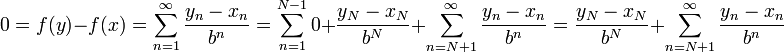
נשים לב כי הביטוי 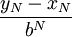 הוא לכל הפחות
הוא לכל הפחות 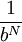 (זה קורה כאשר
(זה קורה כאשר 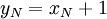 ).
).
כדי לאפס את אגף ימין במשוואה הגדולה, נשאלת השאלה עד כמה שלילי יכול זנב הטור, 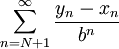 להיות?
להיות?
את התשובה נקבל אם נדרוש כי לכל 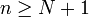 יתקיים
יתקיים 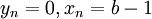 , ואז זנב הטור הוא
, ואז זנב הטור הוא 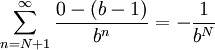 .
.
מכאן רואים שאסור שההפרש 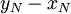 יהיה גדול ממש מ-1, כי אז לא נוכל לאפס את אגף ימין בעזרת זנב הטור.
יהיה גדול ממש מ-1, כי אז לא נוכל לאפס את אגף ימין בעזרת זנב הטור.
בסה"כ יש לנו שתי הצגות עבור  :
:
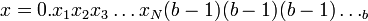 וגם
וגם 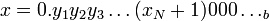
ההצגה השנייה נותנת 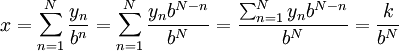
שימו לב שזה לא למבחן, פשוט נשאלה השאלה בתרגול ורציתי לתת תשובה מסודרת. אם יש טעויות או שאלות אפשר לשלוח לי מייל. --Michael 21:13, 9 בדצמבר 2012 (IST)