המספר e
המספר e
לסדרה 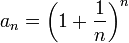 יש גבול ממשי (כפי שמוכח בהמשך). אנו מגדירים את המספר e להיות גבול הסדרה הזו.
יש גבול ממשי (כפי שמוכח בהמשך). אנו מגדירים את המספר e להיות גבול הסדרה הזו.
משפט. תהי  סדרה כלשהי המתכנסת במובן הרחב לאינסוף, אזי
סדרה כלשהי המתכנסת במובן הרחב לאינסוף, אזי 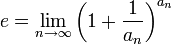
משפט. תהי  סדרה כלשהי המתכנסת במובן הרחב לאינסוף, ותהי
סדרה כלשהי המתכנסת במובן הרחב לאינסוף, ותהי  סדרה המתכנסת (במובן הצר, או במובן הרחב) לגבול L. אזי
סדרה המתכנסת (במובן הצר, או במובן הרחב) לגבול L. אזי 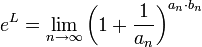
תרגיל.
חשב את גבול הסדרה 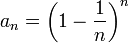
פתרון. נפתח את הסדרה על מנת לקבל ביטוי מהצורה של המשפט למעלה.
כיון ש- 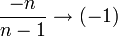 אנו מקבלים כי
אנו מקבלים כי
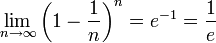
תכונות
הסדרה 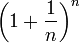 מתכנסת לגבול ממשי, וכמו כן לכל מספר טבעי n מתקיים כי:
מתכנסת לגבול ממשי, וכמו כן לכל מספר טבעי n מתקיים כי:
- הוכחה
אפשר להוכיח כי הסדרה השמאלית מונוטונית עולה, ונוכיח כי הסדרה הימנית מונוטונית יורדת.
מובן מאליו כי
אם כך, שתי הסדרות מונוטוניות וחסומות ולכן מתכנסות.
כמו כן:
וביחד אנו מקבלים את מה שרצינו להוכיח, כיוון שסדרה מונוטונית עולה תמיד קטנה מגבולה, וסדרה מונוטונית יורדת גדולה מגבולה.
נוכיח כי הסדרה הימנית מונוטונית יורדת:
נסמן
רוצים להוכיח
כלומר
נפתח את אי-השוויון:
כעת נשים לב כי לפי פיתוח הבינום של ניוטון מתקיים:
לכן מספיק להוכיח כי
אבל קל לראות כי אי שיוויון זה מתקיים תמיד:
דוגמאות
תרגיל.
מצא את גבול הסדרה ![\lim\limits_{n\to\infty}\frac{n}{\sqrt[n]{n!}}](/images/math/c/0/b/c0b34d8ab1978ef81b477c32f91c3140.png)
לכן לפי משפט אם 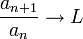 אזי גם
אזי גם ![\sqrt[n]{a_n}\to L](/images/math/7/f/7/7f7539c485ff43f355fd570d12264849.png) .
.
לכן הגבול הנו:
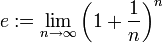
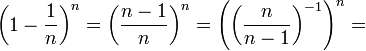
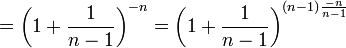
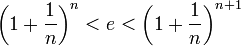
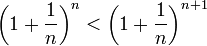
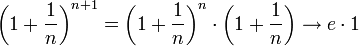
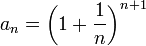
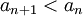
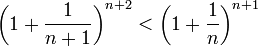
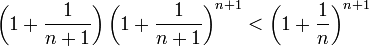
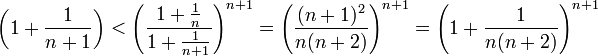
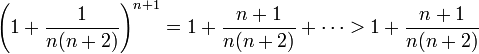
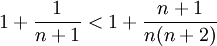
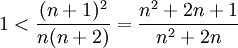
![\frac{n}{\sqrt[n]{n!}}=\sqrt[n]{\frac{n^n}{n!}}](/images/math/4/9/e/49e297f6a8207802bff04ec879e3f5ca.png)