הבדלים בין גרסאות בדף "אנליזת פורייה ויישומים קיץ תשעב/סיכומים/הרצאות/30.7.12"
(יצירת דף עם התוכן "michael.michaeli (@) gmail.com ---- ''הערה:'' השיעור החל בחזרה על כמה מהמושגים הבסיסיים באלגברה לינארית: מר...") |
|||
| שורה 1: | שורה 1: | ||
michael.michaeli (@) gmail.com | michael.michaeli (@) gmail.com | ||
| + | |||
| + | ספר מומלץ: "טורי פורייה והתמרות אינטגרליות", זעפרני ואלון פינקוס. | ||
| + | |||
| + | אתר הקורס: http://www.math.biu.ac.il/~michelm2, Fourie Analasis (88-235‎) | ||
---- | ---- | ||
| − | ''הערה:'' השיעור החל בחזרה על כמה מהמושגים הבסיסיים באלגברה לינארית: מרחב לינארי, צירוף לינארי, תלות וקטורים, בסיס, מרחבים לינאריים של פונקציות (כגון <math>F(-\infty,\infty),C^n(-\infty,\infty)</math>), מכפלה פנימית (כגון <math>\langle f,g\rangle=\int\limits_a^b f(x)g(x)\mathrm dx</math> ב־<math>C[a,b]</math>), נורמה, אי־שיוויון קושי־שוורץ (Cauchy-Schwarz)‏ (<math>|\langle\mathbf u,\mathbf v\rangle|\le\|\mathbf u\|\cdot\|\mathbf v\|</math>), מרחבי הסדרות <math>\ell_p=\left\{(x_n)_{n\in\mathbb N}\in\mathbb C^\infty:\ \sum_{n=1}^\infty|x_n|^p<\infty\right\}</math> עם <math>\langle x,y\rangle=\sum_{n=1}^\infty x_i \overline{y_i}</math> | + | ''הערה:'' השיעור החל בחזרה על כמה מהמושגים הבסיסיים באלגברה לינארית: מרחב לינארי, צירוף לינארי, תלות וקטורים, בסיס, מרחבים לינאריים של פונקציות (כגון <math>F(-\infty,\infty),C^n(-\infty,\infty)</math>), מכפלה פנימית (כגון <math>\langle f,g\rangle=\int\limits_a^b f(x)g(x)\mathrm dx</math> ב־<math>C[a,b]</math>), נורמה, אי־שיוויון קושי־שוורץ (Cauchy-Schwarz)‏ (<math>|\langle\mathbf u,\mathbf v\rangle|\le\|\mathbf u\|\cdot\|\mathbf v\|</math>), מרחבי הסדרות <math>\ell_p=\left\{(x_n)_{n\in\mathbb N}\in\mathbb C^\infty:\ \sum_{n=1}^\infty|x_n|^p<\infty\right\}</math> עם <math>\langle x,y\rangle=\sum_{n=1}^\infty x_i \overline{y_i}</math> ואורתוגונליות. חזרה זו אינה מופיעה כאן במלואה, אך נפרט את הנושאים הקשים לזכירה והחדשים: |
== אי־שיוויון הולדר (Holder) == | == אי־שיוויון הולדר (Holder) == | ||
| שורה 9: | שורה 13: | ||
=== הוכחה === | === הוכחה === | ||
| − | נעזר באי־שיוויון יונג (Jung):‏ <math>\forall\alpha,\beta>0:\ \forall p,q>1\ \and\ \frac1p+\frac1q=1:\ \alpha\cdot\beta\le\frac{\alpha^p}p+\frac{\beta^q}q</math>. נבחר עבור <math>n</math> כרצוננו <math>\alpha=\frac{|x_n|}{\|x\|_p},\beta=\frac{|y_n|}{\|y\|_q}</math>, ונסכום לכל <math>n</math>: <math>\sum_{n=1}^\infty\frac{|x_n|}{\|x\|_p}\frac{|y_n|}{\|y\|_q}\le\sum_{n=1}^\infty\left(\frac{|x_n|^p}{\|x\|_p^p\cdot p}+\frac{|y_n|^q}{\|y\|_q^q\cdot q}\right)=\frac1p+\frac1q=1</math>. נכפול ב־<math>\|x\|_p\|y\|_q</math> | + | נעזר באי־שיוויון יונג (Jung):‏ <math>\forall\alpha,\beta>0:\ \forall p,q>1\ \and\ \frac1p+\frac1q=1:\ \alpha\cdot\beta\le\frac{\alpha^p}p+\frac{\beta^q}q</math>. נבחר עבור <math>n</math> כרצוננו <math>\alpha=\frac{|x_n|}{\|x\|_p},\beta=\frac{|y_n|}{\|y\|_q}</math>, ונסכום לכל <math>n</math>: <math>\sum_{n=1}^\infty\frac{|x_n|}{\|x\|_p}\frac{|y_n|}{\|y\|_q}\le\sum_{n=1}^\infty\left(\frac{|x_n|^p}{\|x\|_p^p\cdot p}+\frac{|y_n|^q}{\|y\|_q^q\cdot q}\right)=\frac1p+\frac1q=1</math>. נכפול ב־<math>\|x\|_p\|y\|_q</math> ונקבל את הדרוש. {{משל}} |
| + | |||
| + | == קירוב לווקטור == | ||
| + | נניח ש־<math>V</math> מרחב לינארי, <math>W</math> תת־מרחב ו־<math>\mathbf u\in V\setminus W</math>. נרצה להראות שקיים וקטור יחיד <math>\tilde\mathbf u\in W</math> שהוא קירוב ל־<math>\mathbf u</math> ב־<math>W</math>, כלומר שעבורו <math>\min_{\mathbf v\in W}\|\mathbf u-\mathbf v\|=\|\mathbf u-\tilde\mathbf u\|</math>. | ||
| + | |||
| + | === מובן של מציאת קירוב === | ||
| + | הקירוב הטוב ביותר ל־<math>\mathbf u</math> ב־<math>W=\mbox{span}(\{\mathbf e_1,\dots,\mathbf e_n\})</math> הוא <math>\tilde\mathbf u=\sum_{k=1}^n\langle\mathbf u,\mathbf e_k\rangle\mathbf e_k</math>. | ||
| + | |||
| + | ==== טענת עזר ==== | ||
| + | יהי <math>V</math> מרחב מכפלה פנימית, ותהי <math>S=\{\mathbf e_1,\dots,\mathbf e_n\}</math> קבוצה אורתונורמלית ב־<math>V</math>. אם <math>\mathbf u=\sum_{k=1}^n a_k\mathbf e_k</math> אזי <math>\forall k:\ a_k=\langle\mathbf u,\mathbf e_k\rangle</math>. | ||
| + | |||
| + | ===== הוכחה ===== | ||
| + | {{left|<math>\langle\mathbf u,\mathbf e_k\rangle=\left\langle\sum_{i=1}^n a_i\mathbf e_i,\mathbf e_k\right\rangle=\sum_{i=1}^n a_i\langle\mathbf e_i,\mathbf e_k\rangle=\sum_{i=1}^n a_i\delta_{i,k}=a_k</math>}}{{משל}} | ||
| + | |||
| + | {{המשך סיכום|תאריך=31.7.12}} | ||
| + | |||
| + | ==== הוכחה ==== | ||
| + | '''הגדרה:''' <math>c_k=\langle\mathbf u,\mathbf e_k\rangle</math> נקרא ''"מקדם פורייה"''. | ||
| + | |||
| + | צריך להוכיח ש־<math>\min_{\mathbf v\in W}\|\mathbf u-\mathbf v\|=\|\mathbf u-\tilde\mathbf u\|</math>. אזי יהי <math>\mathbf v\in W</math> ונסמן <math>\mathbf v=\sum_{k=1}^n a_k\mathbf e_k</math>. לכן | ||
| + | {| | ||
| + | {{=|l=\left\Vert\mathbf u-\mathbf v\right\Vert^2 |r=\langle\mathbf u-\mathbf v,\mathbf u-\mathbf v\rangle }} | ||
| + | {{=|r=\langle\mathbf u,\mathbf u\rangle-\left\langle\mathbf u,\sum_{k=1}^n a_k\mathbf e_k\right\rangle-\left\langle\sum_{k=1}^n a_k\mathbf e_k,\mathbf u\right\rangle+\langle\mathbf v,\mathbf v\rangle }} | ||
| + | {{=|r=\Vert\mathbf u\Vert^2-\sum_{k=1}^n\Big(\overline{a_k}c_k+a_k\overline{c_k}\Big)+\sum_{k=1}^n\vert a_k\vert^2 }} | ||
| + | {{=|r=\Vert\mathbf u\Vert^2+\sum_{k=1}^n\vert c_k-a_k\vert^2-\sum_{k=1}^n\vert c_k\vert^2 |c=מתקיים<br><math>\begin{array}{l}|c_k-a_k|^2-|c_k|^2=\\=(c_k-a_k)(\overline{c_k}-\overline{a_k})-|c_k|^2=\\=|a_k|^2-\overline{a_k}c_k-a_k\overline{c_k}\end{array}</math>}} | ||
| + | {{=|o=\ge |r=\Vert\mathbf u\Vert^2-\sum_{k=1}^n\vert c_k\vert^2 |c=המקרה המינימלי הוא כאשר <math>\forall k:\ a_k=c_k</math>}} | ||
| + | |} | ||
| + | מכאן ש־<math>\|\mathbf u-\mathbf v\|</math> מינימלי כאשר <math>\mathbf v=\tilde\mathbf u</math>. {{משל}} התוצאה נותנת לנו גם את אי־שיוויון בסל: <math>\|\mathbf u\|^2\ge\sum_{k=1}^n|c_k|^2</math>. | ||
| + | |||
| + | {{פס| | ||
| + | ==== הכללה ==== | ||
| + | בהינתן בסיס אורתוגונלי <math>S=\{\mathbf b_1,\dots,\mathbf b_n\}</math> של <math>W</math> (שאינו בהכרח אורתונורמלי) ניתן להכליל את הנוסחה הנ״ל ל־<math>\tilde\mathbf u=\sum_{k=1}^n\frac{\langle\mathbf u,\mathbf b_k\rangle}{\langle\mathbf b_k,\mathbf b_k\rangle}\mathbf b_k</math>. | ||
| − | == | + | ===== הוכחה ===== |
| − | + | <math>S</math> בסיס ולכן וקטור האפס אינו נמצא בו. לפיכך הקבוצה <math>\left\{\frac{\mathbf b_1}{\|\mathbf b_1\|},\dots,\frac{\mathbf b_n}{\|\mathbf b_n\|}\right\}</math> מוגדרת ואורתונורמלית, ולבסוף {{left|<math>\sum_{k=1}^n\frac{\langle\mathbf u,\mathbf b_k\rangle}{\langle\mathbf b_k,\mathbf b_k\rangle}\mathbf b_k=\sum_{k=1}^n\frac{\overline{\|\mathbf b_k\|}\left\langle\mathbf u,\frac{\mathbf b_k}{\|\mathbf b_k\|}\right\rangle}{\|\mathbf b_k\|^2}\|\mathbf b_k\|\frac{\mathbf b_k}{\|\mathbf b_k\|}=\sum_{k=1}^n\left\langle\mathbf u,\frac{\mathbf b_k}{\|\mathbf b_k\|}\right\rangle\frac{\mathbf b_k}{\|\mathbf b_k\|}=\tilde\mathbf u</math>}} | |
| + | {{משל}} | ||
| + | }} | ||
| − | + | === תרגיל === | |
| + | נתבונן בממ״פ של פונקציות רציפות בקטע <math>[-1,1]</math>. נגדיר מ״פ באופן הבא: <math>\langle f,g\rangle=\int\limits_{-1}^1 f(x)g(x)\mathrm dx</math>. מצאו קירוב ל־<math>f(x)=x^3</math> בתת־מרחב הנפרש ע״י המערכת האורתונורמלית <math>S=\{\mathbf e_1,\mathbf e_2\}=\left\{\frac1\sqrt2,\sqrt\frac32 x\right\}</math>. | ||
| − | + | ==== פתרון ==== | |
| − | ולפיכך <math>\left\|x^3-\frac35x\right\|</math> מינימלי. | + | מתקיים:{{left|<math>\begin{align}&\langle f,\mathbf e_1\rangle=\int\limits_{-1}^1\frac{x^3}\sqrt2\mathrm dx=0\\&\langle f,\mathbf e_2\rangle=\int\limits_{-1}^1\sqrt\frac32x^3\mathrm dx=\frac\sqrt65\\\implies&\tilde f(x)=0\cdot\mathbf e_1+\frac\sqrt65\mathbf e_2=\frac\sqrt65\sqrt\frac32x=\frac35x\end{align}</math>}} |
| + | ולפיכך <math>\left\|x^3-\frac35x\right\|</math> מינימלי בקטע. {{משל}} | ||
גרסה מ־16:27, 31 ביולי 2012
michael.michaeli (@) gmail.com
ספר מומלץ: "טורי פורייה והתמרות אינטגרליות", זעפרני ואלון פינקוס.
אתר הקורס: http://www.math.biu.ac.il/~michelm2, Fourie Analasis (88-235)
הערה: השיעור החל בחזרה על כמה מהמושגים הבסיסיים באלגברה לינארית: מרחב לינארי, צירוף לינארי, תלות וקטורים, בסיס, מרחבים לינאריים של פונקציות (כגון 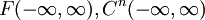 ), מכפלה פנימית (כגון
), מכפלה פנימית (כגון 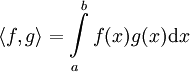 ב־
ב־![C[a,b]](/images/math/d/9/3/d930e3053f32dbc51f14e870df59674d.png) ), נורמה, אי־שיוויון קושי־שוורץ (Cauchy-Schwarz) (
), נורמה, אי־שיוויון קושי־שוורץ (Cauchy-Schwarz) (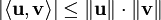 ), מרחבי הסדרות
), מרחבי הסדרות 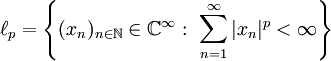 עם
עם 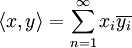 ואורתוגונליות. חזרה זו אינה מופיעה כאן במלואה, אך נפרט את הנושאים הקשים לזכירה והחדשים:
ואורתוגונליות. חזרה זו אינה מופיעה כאן במלואה, אך נפרט את הנושאים הקשים לזכירה והחדשים:
תוכן עניינים
אי־שיוויון הולדר (Holder)
אם 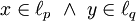 כאשר
כאשר 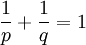 (כלומר,
(כלומר, 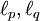 צמודים) אזי
צמודים) אזי 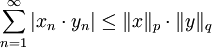 .
.
הוכחה
נעזר באי־שיוויון יונג (Jung): 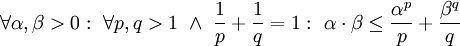 . נבחר עבור
. נבחר עבור  כרצוננו
כרצוננו 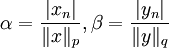 , ונסכום לכל
, ונסכום לכל  :
: 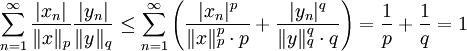 . נכפול ב־
. נכפול ב־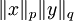 ונקבל את הדרוש.
ונקבל את הדרוש. 
קירוב לווקטור
נניח ש־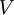 מרחב לינארי,
מרחב לינארי, 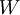 תת־מרחב ו־
תת־מרחב ו־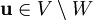 . נרצה להראות שקיים וקטור יחיד
. נרצה להראות שקיים וקטור יחיד 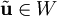 שהוא קירוב ל־
שהוא קירוב ל־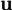 ב־
ב־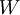 , כלומר שעבורו
, כלומר שעבורו 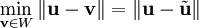 .
.
מובן של מציאת קירוב
הקירוב הטוב ביותר ל־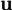 ב־
ב־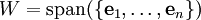 הוא
הוא 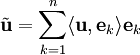 .
.
טענת עזר
יהי 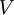 מרחב מכפלה פנימית, ותהי
מרחב מכפלה פנימית, ותהי 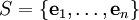 קבוצה אורתונורמלית ב־
קבוצה אורתונורמלית ב־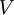 . אם
. אם 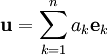 אזי
אזי 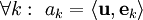 .
.
הוכחה
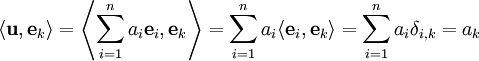

את ההמשך עשינו בשיעור שאחריו:
הוכחה
הגדרה: 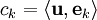 נקרא "מקדם פורייה".
נקרא "מקדם פורייה".
צריך להוכיח ש־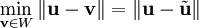 . אזי יהי
. אזי יהי 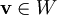 ונסמן
ונסמן 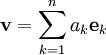 . לכן
. לכן
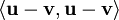
|

|
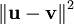
|
||||
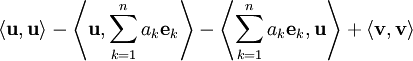
|

|
|||||
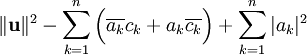
|

|
|||||
מתקיים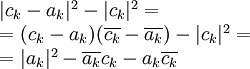
|
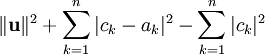
|

|
||||
המקרה המינימלי הוא כאשר 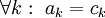
|
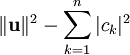
|
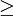
|
מכאן ש־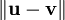 מינימלי כאשר
מינימלי כאשר 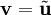 .
.  התוצאה נותנת לנו גם את אי־שיוויון בסל:
התוצאה נותנת לנו גם את אי־שיוויון בסל: 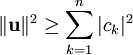 .
.
הכללה
בהינתן בסיס אורתוגונלי 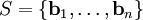 של
של 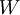 (שאינו בהכרח אורתונורמלי) ניתן להכליל את הנוסחה הנ״ל ל־
(שאינו בהכרח אורתונורמלי) ניתן להכליל את הנוסחה הנ״ל ל־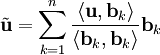 .
.
הוכחה
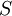 בסיס ולכן וקטור האפס אינו נמצא בו. לפיכך הקבוצה
בסיס ולכן וקטור האפס אינו נמצא בו. לפיכך הקבוצה 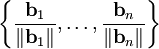 מוגדרת ואורתונורמלית, ולבסוף
מוגדרת ואורתונורמלית, ולבסוף 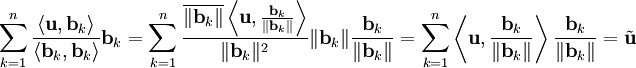

תרגיל
נתבונן בממ״פ של פונקציות רציפות בקטע ![[-1,1]](/images/math/d/0/6/d060b17b29e0dae91a1cac23ea62281a.png) . נגדיר מ״פ באופן הבא:
. נגדיר מ״פ באופן הבא: 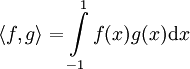 . מצאו קירוב ל־
. מצאו קירוב ל־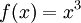 בתת־מרחב הנפרש ע״י המערכת האורתונורמלית
בתת־מרחב הנפרש ע״י המערכת האורתונורמלית 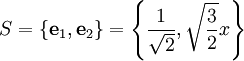 .
.
פתרון
מתקיים: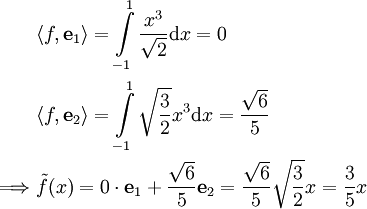
ולפיכך 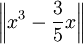 מינימלי בקטע.
מינימלי בקטע. 