אנליזת פורייה ויישומים קיץ תשעב/סיכומים/הרצאות/30.7.12
מתוך Math-Wiki
גרסה מ־14:37, 30 ביולי 2012 מאת אור שחף (שיחה | תרומות) (יצירת דף עם התוכן "michael.michaeli (@) gmail.com ---- ''הערה:'' השיעור החל בחזרה על כמה מהמושגים הבסיסיים באלגברה לינארית: מר...")
michael.michaeli (@) gmail.com
הערה: השיעור החל בחזרה על כמה מהמושגים הבסיסיים באלגברה לינארית: מרחב לינארי, צירוף לינארי, תלות וקטורים, בסיס, מרחבים לינאריים של פונקציות (כגון 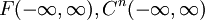 ), מכפלה פנימית (כגון
), מכפלה פנימית (כגון 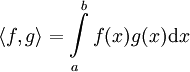 ב־
ב־![C[a,b]](/images/math/d/9/3/d930e3053f32dbc51f14e870df59674d.png) ), נורמה, אי־שיוויון קושי־שוורץ (Cauchy-Schwarz) (
), נורמה, אי־שיוויון קושי־שוורץ (Cauchy-Schwarz) (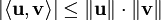 ), מרחבי הסדרות
), מרחבי הסדרות 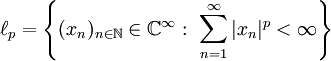 עם
עם 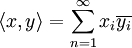 , אורתוגונליות. חזרה זו אינה מופיעה כאן במלואה, אך נפרט את הנושאים החדשים והקשים לזכירה:
, אורתוגונליות. חזרה זו אינה מופיעה כאן במלואה, אך נפרט את הנושאים החדשים והקשים לזכירה:
אי־שיוויון הולדר (Holder)
אם 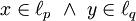 כאשר
כאשר 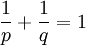 (כלומר,
(כלומר, 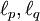 צמודים) אזי
צמודים) אזי 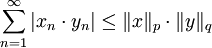 .
.
הוכחה
נעזר באי־שיוויון יונג (Jung): 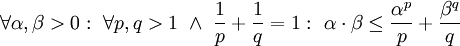 . נבחר עבור
. נבחר עבור  כרצוננו
כרצוננו 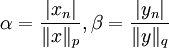 , ונסכום לכל
, ונסכום לכל  :
: 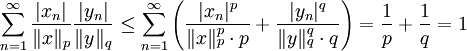 . נכפול ב־
. נכפול ב־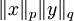
תהליך גרם־שמידט (Gram-Schmidt)
התהליך מאשר להפוך כל קבוצה 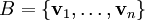 בת״ל לקבוצה
בת״ל לקבוצה 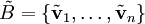 אורתונורמלית כך ש־
אורתונורמלית כך ש־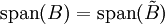 .
.
טענת עזר: יהי  מרחב מכפלה פנימית, ותהי
מרחב מכפלה פנימית, ותהי 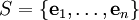 קבוצה אורתונורמלית ב־
קבוצה אורתונורמלית ב־ . אם
. אם 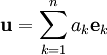 אזי
אזי 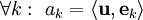 . הוכחה:
. הוכחה: 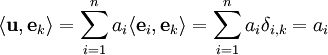
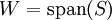 תת־מרחב של
תת־מרחב של  ואם
ואם 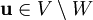 אזי ברור ש־
אזי ברור ש־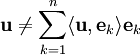 . במקרה זה קיים איבר אחר
. במקרה זה קיים איבר אחר 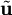 שהוא הקירוב הטוב ביותר ל־
שהוא הקירוב הטוב ביותר ל־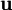 ב־
ב־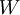 (כלומר,
(כלומר, 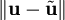 מינימלי), ומתקיים
מינימלי), ומתקיים 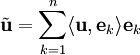 . דוגמה: נתבונן בממ״פ של פונקציות רציפות בקטע
. דוגמה: נתבונן בממ״פ של פונקציות רציפות בקטע ![[-1,1]](/images/math/d/0/6/d060b17b29e0dae91a1cac23ea62281a.png) . נגדיר מ״פ באופן הבא:
. נגדיר מ״פ באופן הבא: 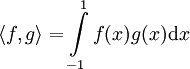 . נמצא קירוב ל־
. נמצא קירוב ל־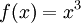 בתת־מרחב הנפרש ע״י המערכת האורתונורמלית
בתת־מרחב הנפרש ע״י המערכת האורתונורמלית 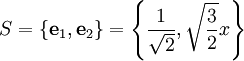 . מתקיים:
. מתקיים: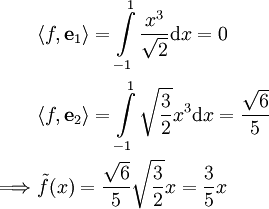
ולפיכך 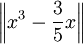 מינימלי.
מינימלי.