הבדלים בין גרסאות בדף "מדר קיץ תשעב/סיכומים/הרצאות/2.8.12"
(יצירת דף עם התוכן "פתרון המד״ר משיעור קודם: <math>\frac{\ln\left(\frac y{x+2}+\sqrt3-1\right)-\ln\left(-\frac y{x+2}+\sqrt3+1\right)}\sqrt3-\frac12\ln\left|2+\frac...") |
|||
| שורה 1: | שורה 1: | ||
| − | + | = מד״ר מסדר שני = | |
| + | הצורה הכללית של מד״ר כזו היא <math>F(x,y,y',y'')=0</math>, והפתרון הוא מהצורה <math>y=\varphi(x,c_1,c_2)</math>. | ||
| + | == בעיית קושי מסדר 2 == | ||
| + | זו בעיה שבה אנו נדרשים לפתור מד״ר עם שני תנאי התחלה <math>\begin{cases}y(x_0)=y_0\\y'(x_0)=y_0'\end{cases}</math> (מובן ש־<math>y_0'</math> אינו הנגזרת של הקבוע <math>y_0</math>, אלא ערך הנגזרת בנקודה <math>x_0</math>). | ||
| − | == | + | == סוגים נפוצים == |
| − | + | === סוג 1 === | |
| + | מתקיים <math>y^{(n)}=f(x)</math>. ניתן לפתור זאת ע״י אינטגרציה <math>n</math> פעמים (במקרה שלנו, <math>n=2</math>). | ||
| − | === | + | === סוג 2 === |
| − | + | אלה מד״ר שבהן ניתן להוריד את סדר המשוואה. עבור מד״ר מסדר 2, נחלק לשני מקרים: | |
| − | ==== | + | ==== מקרה 1 ==== |
| − | + | <math>y</math> לא מופיע במשוואה, כלומר המשוואה מהצורה <math>y''=f(x,y')</math>. במקרה זה נציב <math>z=y'</math> ונקבל מד״ר מסדר ראשון. | |
| − | ==== | + | ===== תרגיל ===== |
| − | + | פתרו את המד״ר <math>y''=x y'</math>. | |
| − | + | ====== פתרון ====== | |
| + | {| | ||
| + | {{=|o=\implies |r=z'=xz | c=נציב <math>z=y'</math> ולכן:}} | ||
| + | {{=|o=\implies |r=\frac{z'}z=x }} | ||
| + | {{=|o=\implies |r=\int\frac{\mathrm dz}z=\int x\mathrm dx }} | ||
| + | {{=|o=\implies |r=\ln\vert z\vert=\frac{x^2}2+c_0 }} | ||
| + | {{=|o=\implies |r=z=y'=c_1\mathrm e^{\frac{x^2}2} |c=נסמן <math>c_1:=\mathrm e^{c_0}</math>:}} | ||
| + | {{=|o=\implies |r=y=c_1\int\mathrm e^{\frac{x^2}2}\mathrm dx }} | ||
| + | |} | ||
| + | {{משל}} | ||
| − | + | ==== מקרה 2 ==== | |
| + | <math>x</math> לא מופיע במשוואה, כלומר המד״ר מהצורה <math>y''=f(y,y')</math>. שוב נגדיר <math>z=y'</math>, ואז <math>y''=z'=\frac{\mathrm dz}{\mathrm dy}\frac{\mathrm dy}{\mathrm dx}=z_y' z</math>. המד״ר הופכת ל־<math>zz_y'=f(y,z)</math>, כלומר מד״ר מסדר ראשון של <math>y,z</math>. נובע ש־<math>x=\int\frac{\mathrm dy}z</math>. | ||
| − | === | + | ===== תרגיל ===== |
| − | מד״ר מהצורה <math>y'+f(x)y^2+g(x)y+h(x)=0</math>. פתרון כללי של משוואת ריקטי הוא מהצורה <math>y=\frac{c a(x)+b(x)}{c A(x)+B(x)}</math>, ולכל ביטוי מהצורה הנ״ל קיימת משוואת ריקטי מתאימה. | + | פתרו <math>yy''-2(y')^2=0</math>. |
| + | |||
| + | ====== פתרון ====== | ||
| + | נציב <math>z</math> באופן הנ״ל ונקבל | ||
| + | {{left|<math>\begin{align}&y\frac{\mathrm dz}{\mathrm dy}z=2z^2\\\implies&\int\frac{\mathrm dz}{2z}=\int\frac{\mathrm dy}y\\\implies&\frac12\ln|z|=\ln|y|+C_1\\\implies&z=C_2y^2\\\implies&\frac{\mathrm dy}{\mathrm dx}=C_2y^2\\\implies&\int\frac{\mathrm dy}{y^2}=\int C_2\mathrm dx\\\implies&-\frac1y=C_2x+C_3\\\implies&y=\frac{c_2}{c_1x+1}\end{align}</math>}} | ||
| + | {{משל}} | ||
| + | |||
| + | === משוואות ריקטי === | ||
| + | אלה מד״ר מהצורה <math>y'+f(x)y^2+g(x)y+h(x)=0</math>. פתרון כללי של משוואת ריקטי הוא מהצורה <math>y=\frac{c a(x)+b(x)}{c A(x)+B(x)}</math>, ולכל ביטוי מהצורה הנ״ל קיימת משוואת ריקטי מתאימה. | ||
==== הוכחה ==== | ==== הוכחה ==== | ||
| − | ראשית, נוכיח שלכל ביטוי מהצורה הנ״ל קיימת משוואת ריקטי מתאימה: <math>y\cdot(cA+B)=ca+b</math> ולכן <math>c(yA-a)-b+yB=0</math>. נגזור את שני האגפים ונקבל <math>c(y'A+A'y-a')-b'+(y'B+B'y)=0</math>. שתי המשוואות האחרונות | + | ראשית, נוכיח שלכל ביטוי מהצורה הנ״ל קיימת משוואת ריקטי מתאימה: מתקיים <math>y\cdot(cA+B)=ca+b</math> ולכן <math>c(yA-a)-b+yB=0</math>. נגזור את שני האגפים ונקבל <math>c(y'A+A'y-a')-b'+(y'B+B'y)=0</math>. נציג את שתי המשוואות האחרונות בצורה <math>{\color{Blue}\begin{pmatrix}y'A+A'y-a'&-b'+y'B+B'y\\yA-a&-b+yB\end{pmatrix}}\begin{pmatrix}c\\1\end{pmatrix}=\begin{pmatrix}0\\0\end{pmatrix}</math> ונשים לב שהמטריצה הכחולה מאפסת וקטור שאינו וקטור האפס, ולפיכך הדטרמיננטה שלה היא 0: <math>\begin{vmatrix}y'A+A'y-a'&-b'+y'B+B'y\\yA-a&-b+yB\end{vmatrix}=0</math>. נחשב את הדטרמיננטה ונגלה ש־<math>y'+y^2\frac{AB'-B'a}{Ab-aB}+y\frac{a'B-A'B-Ab'-aB'}{bA-aB}+\frac{ab'-a'b}{bA-aB}=0</math>, כדרוש. |
| − | |||
| − | + | לצד השני, יהי <math>y_z(x)</math> פתרון רגולרי של משוואת ריקטי. נציב במד״ר <math>y(x)=y_z(x)+z(x)</math> (כאשר <math>z</math> פונקציה לא ידועה) ונגלה ש־ | |
| − | + | {| | |
| + | {{=|o= |r=z'+y_z'+f(x)\left(z^2+2zy_z+y_z^2\right)+g(x)(y_z+z)+h(x)=0 }} | ||
| + | {{=|o=\implies |r=\Big(z'+z^2+(2f(x)y_z+g(x))z\Big)+\Big(y_z'+f(x)y_z^2+g(x)y_z+h(x)\Big)=0 }} | ||
| + | {{=|o=\implies |r=z'+z^2+(2f(x)y_z+g(x))z=0 |c=<math>y_z</math> פתרון, לכן: }} | ||
| + | |} | ||
| + | לכן <math>z</math> פתרון של משוואת ברנולי עם <math>y^2</math>, ולפיכך הוא מהצורה <math>z=\frac1{c\alpha(x)+\beta(x)}</math>. לבסוף הפתרון מהצורה <math>y=y_z+z=\frac{cy_z(x)\alpha(x)+y_z(x)z(x)+1}{c\alpha(x)+\beta(x)}</math>. {{משל}} | ||
| − | === | + | = מערכת מד״ר מסדר ראשון = |
| − | <math>y_1'+\sin(x)+y_1y_2x^2=0 | + | זו מערכת מהצורה <math>\vec F(x,\vec y,\vec y\,')=0</math> כאשר <math>\vec F</math> היא מערכת של <math>n</math> פונקציות. המערכת היא ב־<math>2n+1</math> משתנים. בצורה נורמלית: <math>\vec y\,'=\vec f(x,\vec y)</math>. לפיכך הפתרון הכללי הינו מהצורה <math>\begin{pmatrix}y_1\\y_2\end{pmatrix}=\begin{pmatrix}\varphi_1(x,c_1,c_2)\\\varphi_2(x,c_1,c_2)\end{pmatrix}</math>. לדוגמה, <math>\begin{cases}y_1'+\sin(x)+y_1y_2x^2=0\\\frac{y_1'}{y_2}+\frac{y_2'}{y_1}+\cos(x)=0\end{cases}</math> היא מערכת מד״ר. |
| − | + | == בעיית קושי == | |
| − | + | במערכת מד״ר מסדר 1, בעיית קושי היא לפתור את המד״ר עם תנאי ההתחלה <math>\vec y(x_0)=\vec y_0</math>. | |
| − | + | == משפט == | |
| − | מד״ר מסדר <math>n</math> (נורמלית/לינארית/ | + | מד״ר מסדר <math>n</math> (נורמלית/לינארית/לינארית־הומוגנית) שקולה למערכת של <math>n</math> מד״ר מסדר ראשון (נורמליות/לינאריות/לינאריות־והומוגניות). אם למד״ר מסדר גבוה נתונים ערכי ההתחלה <math>y(x_0),y'(x_0),\dots,y^{(n-1)}(x_0)</math> אז המד״ר שקולה לבעיית קושי עבור המערכת. |
| − | + | === הוכחה === | |
| − | נתונה המד״ר <math>F(x,y,y',\dots,y^{(n)})=0</math> ונסמן <math>\forall k=1,\dots, n-1:\ y_k=y^{(k)}</math>. לכן <math>F(x,y,y_1,y_2,\dots,y_{ | + | נתונה המד״ר <math>F\left(x,y,y',\dots,y^{(n)}\right)=0</math> ונסמן <math>\forall k=1,\dots, n-1:\ y_k=y^{(k)}</math>. לכן <math>F(x,y,y_1,y_2,\dots,y_{n-1},y_{n-1}')=0</math>. נוסיף את המד״ר הבאות: <math>\forall k=1,\dots,n-1:\ y_k=y_{k-1}'</math>. המערכת שקולה למד״ר המקורית והיא נורמלית/לינארית/לינארית־הומוגנית בהתאם למערכת המקורית. {{משל}} |
| − | + | === דוגמה === | |
| − | <math>y^{(3)}+x^2y''+\sin(x)y=0</math>. נציב <math>z=y'</math> ו־<math>w=z'=y''</math> | + | <math>y^{(3)}+x^2y''+\sin(x)y=0</math>. נציב <math>z=y'</math> ו־<math>w=z'=y''</math> ולפיכך <math>\begin{cases}w'+x^2w+\sin(x)y=0\\z=y'\\w=z'\end{cases}</math>. |
== מד״ר סתומות מסדר 1 == | == מד״ר סתומות מסדר 1 == | ||
אלה מד״ר <math>F(x,y,y')=0</math> שאנו לא יודעים כיצד להביאן לצורה נורמלית. | אלה מד״ר <math>F(x,y,y')=0</math> שאנו לא יודעים כיצד להביאן לצורה נורמלית. | ||
| − | + | === סוגים נפוצים === | |
| + | ==== מקרה 1 ==== | ||
| + | משוואה מסדר 1 וממעלה <math>n</math>: <math>\sum_{k=0}^{n-1}p_k(x,y)(y')^k+(y')^n=0</math>. מכאן שקיימות פונקציות <math>f_k,\quad k\in\{1,2,\dots,n\}</math> שעבורן <math>\prod_{k=1}^n\Big(y'-f_k(x,y)\Big)=0</math>. | ||
| + | |||
| + | ===== תרגיל ===== | ||
| + | פתרו <math>(y')^2-\frac{xy}{a^2}=0</math>. | ||
| + | |||
| + | ====== פתרון ====== | ||
| + | {{left|<math>\begin{align}&\left(y'-\frac\sqrt{xy}a\right)\left(y'+\frac\sqrt{xy}a\right)=0\\\implies&y'=\pm\frac\sqrt{xy}a\\\implies&\frac{y'}\sqrt y=\pm\frac\sqrt xa\\\implies&\int\frac{\mathrm dy}\sqrt y=\pm\int\frac\sqrt xa\mathrm dx\\\implies&2\sqrt y=\pm\frac{2x^{3/2}}{3a}+c\\\implies&y=\frac14\left(c\pm\frac{2\sqrt x^3}{3a}\right)^2\end{align}</math>}} | ||
| + | {{משל}} | ||
| + | |||
| + | ==== מקרה 2 ==== | ||
| + | <math>x</math> לא מופיעה במד״. צורתה <math>F(y,y')=0</math>, ובהצבת <math>z=y'=\frac{\mathrm dy}{\mathrm dx}</math> נקבל <math>F(y,z)=0</math>. נשים לב ש־<math>\frac{\mathrm dz}z=\mathrm dx</math> ולכן <math>x=\int\mathrm dx=\int\frac{\mathrm dy}z=\frac yz+\int\frac y{z^2}\mathrm dz</math>. לפיכך, אם <math>y=\varphi(z)</math> אזי <math>x=\frac{\varphi(z)}z+\int\frac{\varphi(z)}{z^2}\mathrm dz</math>. | ||
| + | |||
| + | ===== תרגיל ===== | ||
| + | פתרו <math>y=(y')^2+2(y')^3</math>. | ||
| + | |||
| + | ====== פתרון ====== | ||
| + | נסמן <math>z=y'</math> ונציב במד״ר: <math>y=z^2+2z^3</math>. עתה <math>x=\frac yz+\int\frac y{z^2}\mathrm dz=\frac{z^2+2z^3}z+\int(1+2z)\mathrm dz=c+z+2z^2+z+z^2=c+2z+3z^2=c+2y'+3(y')^2</math>, וזו מד״ר ממקרה 1, שאותו אנו כבר יודעים לפתור. {{משל}} | ||
| + | |||
| + | ==== מקרה 3 ==== | ||
| + | <math>y</math> לא מופיעה, <math>F(x,y')=0</math>. שוב נציב <math>z=y'</math>, ונניח <math>x=\varphi(y')=\varphi(z)</math>. אזי <math>y=\int z\mathrm dx=zx-\int x\mathrm dz=z\cdot\varphi(z)-\int\varphi(z)\mathrm dz</math>. | ||
| + | |||
| + | ===== תרגיל ===== | ||
| + | פתרו <math>x=y'\sin(y')</math>. | ||
| + | |||
| + | ====== פתרון ====== | ||
| + | אחרי הצבה <math>z=y'</math> נקבל <math>x=z\sin(z)</math> ולבסוף <math>y=z\cdot z\sin(z)-\int z\sin(z)\mathrm dz=c+x+z^2\sin(z)+z\cos(z)-\sin(z)</math>. נציב חזרה <math>z=y'</math> וסיימנו. {{משל}} | ||
| + | |||
| + | ==== מקרה 4 ==== | ||
| + | <math>y</math> מופיעה ו־<math>x</math> לא, כלומר <math>F(y,y')=0</math>, והמד״ר סתומה. כרגיל, נגדיר <math>z=y'</math>. אם <math>y=\varphi(t)</math> ו־<math>z=\psi(t)</math> אזי <math>\mathrm dy=\psi(t)\mathrm dx=\frac{\mathrm d\varphi}{\mathrm dt}(t)\mathrm dt=\varphi_t'(t)\mathrm dt</math>, ומכאן ש־<math>\mathrm dx=\frac{\varphi_t'(t)}{\psi(t)}\mathrm dt</math>. לבסוף, <math>\begin{cases}x=\int\frac{\varphi_t'(t)}{\psi(t)}\mathrm dt\\y=\varphi(t)\end{cases}</math>. | ||
| − | + | ===== תרגיל ===== | |
| + | פתרו <math>y=a\sqrt{1+(y')^2}</math>. | ||
| − | + | ====== פתרון ====== | |
| + | נסמן <math>\psi(t)=\sinh(t)=z</math>, נציב במד״ר ונקבל <math>y=a\cosh(t)=\varphi(t)</math>. כמו כן, <math>x=\int\frac{a\sinh(t)}{\sinh(t)}\mathrm dt=at+c</math>. עתה, <math>t=\frac{c-x}a</math> ולכן <math>y=a\cosh\left(\frac{c-x}a\right)</math>. {{משל}} | ||
| − | + | ==== מקרה 5 ==== | |
| − | + | <math>x</math> מופיעה ו־<math>y</math> לא, כלומר <math>F(x,y')=0</math>, והמד״ר סתומה. נציב <math>z=y',x=\varphi(t)</math> ולכן <math>F(\varphi(t),z)=0</math>. נסמן <math>z=\psi(t)</math> ונגלה כי <math>\mathrm dx=\varphi_t'(t)\mathrm dt=\frac{\mathrm dy}{\psi(t)}</math>. מאינטגרציה ולפי הגדרת <math>\varphi</math> נקבל <math>\begin{cases}y=\int\psi(t)\varphi_t'(t)\mathrm dt\\x=\varphi(t)\end{cases}</math>. | |
| − | + | ||
גרסה מ־12:48, 6 באוגוסט 2012
מד״ר מסדר שני
הצורה הכללית של מד״ר כזו היא 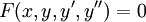 , והפתרון הוא מהצורה
, והפתרון הוא מהצורה 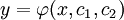 .
.
בעיית קושי מסדר 2
זו בעיה שבה אנו נדרשים לפתור מד״ר עם שני תנאי התחלה 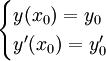 (מובן ש־
(מובן ש־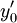 אינו הנגזרת של הקבוע
אינו הנגזרת של הקבוע 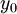 , אלא ערך הנגזרת בנקודה
, אלא ערך הנגזרת בנקודה 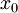 ).
).
סוגים נפוצים
סוג 1
מתקיים 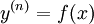 . ניתן לפתור זאת ע״י אינטגרציה
. ניתן לפתור זאת ע״י אינטגרציה  פעמים (במקרה שלנו,
פעמים (במקרה שלנו, 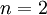 ).
).
סוג 2
אלה מד״ר שבהן ניתן להוריד את סדר המשוואה. עבור מד״ר מסדר 2, נחלק לשני מקרים:
מקרה 1
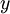 לא מופיע במשוואה, כלומר המשוואה מהצורה
לא מופיע במשוואה, כלומר המשוואה מהצורה 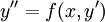 . במקרה זה נציב
. במקרה זה נציב 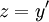 ונקבל מד״ר מסדר ראשון.
ונקבל מד״ר מסדר ראשון.
תרגיל
פתרו את המד״ר 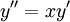 .
.
פתרון
נציב 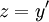 ולכן: ולכן:
|
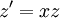
|
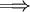
|
||||
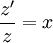
|
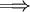
|
|||||
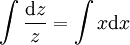
|
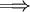
|
|||||
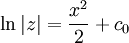
|
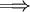
|
|||||
נסמן 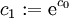 : :
|
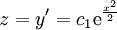
|
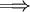
|
||||
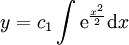
|
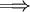
|

מקרה 2
 לא מופיע במשוואה, כלומר המד״ר מהצורה
לא מופיע במשוואה, כלומר המד״ר מהצורה 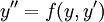 . שוב נגדיר
. שוב נגדיר 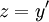 , ואז
, ואז 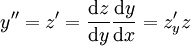 . המד״ר הופכת ל־
. המד״ר הופכת ל־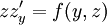 , כלומר מד״ר מסדר ראשון של
, כלומר מד״ר מסדר ראשון של 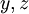 . נובע ש־
. נובע ש־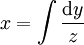 .
.
תרגיל
פתרו 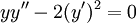 .
.
פתרון
נציב 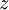 באופן הנ״ל ונקבל
באופן הנ״ל ונקבל
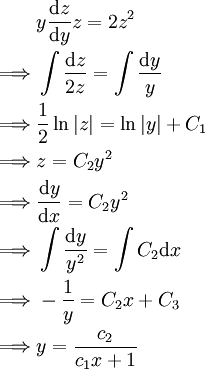

משוואות ריקטי
אלה מד״ר מהצורה 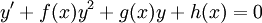 . פתרון כללי של משוואת ריקטי הוא מהצורה
. פתרון כללי של משוואת ריקטי הוא מהצורה 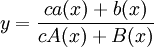 , ולכל ביטוי מהצורה הנ״ל קיימת משוואת ריקטי מתאימה.
, ולכל ביטוי מהצורה הנ״ל קיימת משוואת ריקטי מתאימה.
הוכחה
ראשית, נוכיח שלכל ביטוי מהצורה הנ״ל קיימת משוואת ריקטי מתאימה: מתקיים 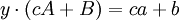 ולכן
ולכן 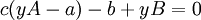 . נגזור את שני האגפים ונקבל
. נגזור את שני האגפים ונקבל 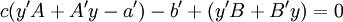 . נציג את שתי המשוואות האחרונות בצורה
. נציג את שתי המשוואות האחרונות בצורה 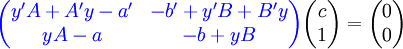 ונשים לב שהמטריצה הכחולה מאפסת וקטור שאינו וקטור האפס, ולפיכך הדטרמיננטה שלה היא 0:
ונשים לב שהמטריצה הכחולה מאפסת וקטור שאינו וקטור האפס, ולפיכך הדטרמיננטה שלה היא 0: 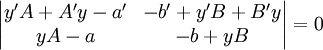 . נחשב את הדטרמיננטה ונגלה ש־
. נחשב את הדטרמיננטה ונגלה ש־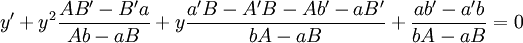 , כדרוש.
, כדרוש.
לצד השני, יהי 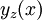 פתרון רגולרי של משוואת ריקטי. נציב במד״ר
פתרון רגולרי של משוואת ריקטי. נציב במד״ר 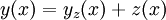 (כאשר
(כאשר  פונקציה לא ידועה) ונגלה ש־
פונקציה לא ידועה) ונגלה ש־
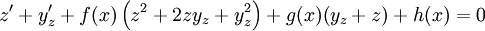
|
||||||
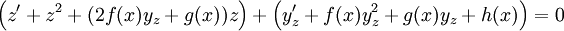
|
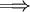
|
|||||
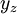 פתרון, לכן: פתרון, לכן:
|
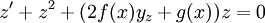
|
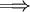
|
לכן 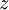 פתרון של משוואת ברנולי עם
פתרון של משוואת ברנולי עם 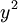 , ולפיכך הוא מהצורה
, ולפיכך הוא מהצורה 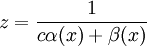 . לבסוף הפתרון מהצורה
. לבסוף הפתרון מהצורה 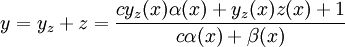 .
. 
מערכת מד״ר מסדר ראשון
זו מערכת מהצורה 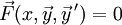 כאשר
כאשר 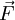 היא מערכת של
היא מערכת של  פונקציות. המערכת היא ב־
פונקציות. המערכת היא ב־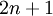 משתנים. בצורה נורמלית:
משתנים. בצורה נורמלית: 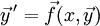 . לפיכך הפתרון הכללי הינו מהצורה
. לפיכך הפתרון הכללי הינו מהצורה 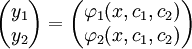 . לדוגמה,
. לדוגמה, 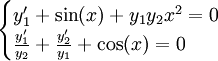 היא מערכת מד״ר.
היא מערכת מד״ר.
בעיית קושי
במערכת מד״ר מסדר 1, בעיית קושי היא לפתור את המד״ר עם תנאי ההתחלה 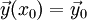 .
.
משפט
מד״ר מסדר  (נורמלית/לינארית/לינארית־הומוגנית) שקולה למערכת של
(נורמלית/לינארית/לינארית־הומוגנית) שקולה למערכת של  מד״ר מסדר ראשון (נורמליות/לינאריות/לינאריות־והומוגניות). אם למד״ר מסדר גבוה נתונים ערכי ההתחלה
מד״ר מסדר ראשון (נורמליות/לינאריות/לינאריות־והומוגניות). אם למד״ר מסדר גבוה נתונים ערכי ההתחלה 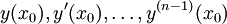 אז המד״ר שקולה לבעיית קושי עבור המערכת.
אז המד״ר שקולה לבעיית קושי עבור המערכת.
הוכחה
נתונה המד״ר 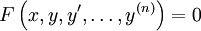 ונסמן
ונסמן 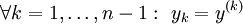 . לכן
. לכן 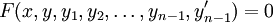 . נוסיף את המד״ר הבאות:
. נוסיף את המד״ר הבאות: 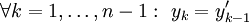 . המערכת שקולה למד״ר המקורית והיא נורמלית/לינארית/לינארית־הומוגנית בהתאם למערכת המקורית.
. המערכת שקולה למד״ר המקורית והיא נורמלית/לינארית/לינארית־הומוגנית בהתאם למערכת המקורית. 
דוגמה
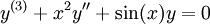 . נציב
. נציב 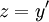 ו־
ו־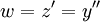 ולפיכך
ולפיכך 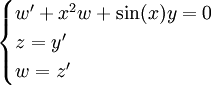 .
.
מד״ר סתומות מסדר 1
אלה מד״ר 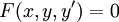 שאנו לא יודעים כיצד להביאן לצורה נורמלית.
שאנו לא יודעים כיצד להביאן לצורה נורמלית.
סוגים נפוצים
מקרה 1
משוואה מסדר 1 וממעלה  :
: 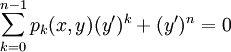 . מכאן שקיימות פונקציות
. מכאן שקיימות פונקציות  שעבורן
שעבורן 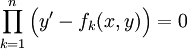 .
.
תרגיל
פתרו 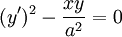 .
.
פתרון
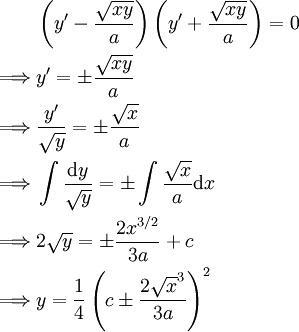

מקרה 2
 לא מופיעה במד״. צורתה
לא מופיעה במד״. צורתה 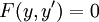 , ובהצבת
, ובהצבת 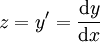 נקבל
נקבל 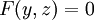 . נשים לב ש־
. נשים לב ש־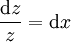 ולכן
ולכן 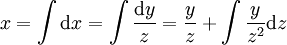 . לפיכך, אם
. לפיכך, אם 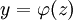 אזי
אזי 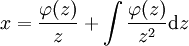 .
.
תרגיל
פתרו 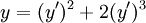 .
.
פתרון
נסמן 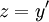 ונציב במד״ר:
ונציב במד״ר: 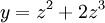 . עתה
. עתה 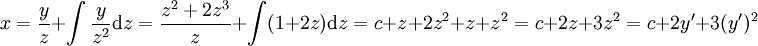 , וזו מד״ר ממקרה 1, שאותו אנו כבר יודעים לפתור.
, וזו מד״ר ממקרה 1, שאותו אנו כבר יודעים לפתור. 
מקרה 3
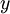 לא מופיעה,
לא מופיעה, 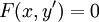 . שוב נציב
. שוב נציב 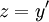 , ונניח
, ונניח 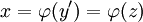 . אזי
. אזי 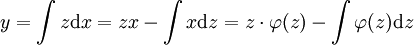 .
.
תרגיל
פתרו 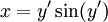 .
.
פתרון
אחרי הצבה 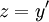 נקבל
נקבל 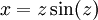 ולבסוף
ולבסוף 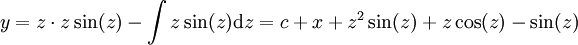 . נציב חזרה
. נציב חזרה 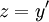 וסיימנו.
וסיימנו. 
מקרה 4
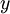 מופיעה ו־
מופיעה ו־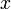 לא, כלומר
לא, כלומר 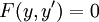 , והמד״ר סתומה. כרגיל, נגדיר
, והמד״ר סתומה. כרגיל, נגדיר 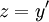 . אם
. אם 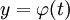 ו־
ו־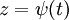 אזי
אזי 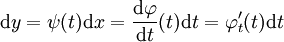 , ומכאן ש־
, ומכאן ש־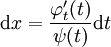 . לבסוף,
. לבסוף, 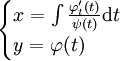 .
.
תרגיל
פתרו 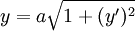 .
.
פתרון
נסמן 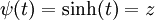 , נציב במד״ר ונקבל
, נציב במד״ר ונקבל 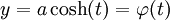 . כמו כן,
. כמו כן, 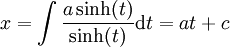 . עתה,
. עתה, 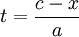 ולכן
ולכן 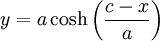 .
. 
מקרה 5
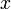 מופיעה ו־
מופיעה ו־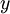 לא, כלומר
לא, כלומר 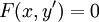 , והמד״ר סתומה. נציב
, והמד״ר סתומה. נציב 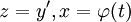 ולכן
ולכן 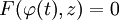 . נסמן
. נסמן 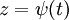 ונגלה כי
ונגלה כי 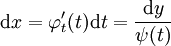 . מאינטגרציה ולפי הגדרת
. מאינטגרציה ולפי הגדרת 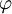 נקבל
נקבל 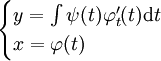 .
.