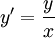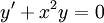הבדלים בין גרסאות בדף "מדר קיץ תשעב/סיכומים/הרצאות/30.7.12"
(יצירת דף עם התוכן "מרצה: ראובן כהן, reuven (@) math.biu.ac.il u.math.biu.ac.il/~reuven/ode.pdf 050-5217779 ----- = מבוא = משוואה דיפרנציאלית הי...") |
|||
| שורה 1: | שורה 1: | ||
| − | + | == מבוא == | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | = מבוא = | + | |
משוואה דיפרנציאלית היא משוואה המקשרת בין משתנה בלתי תלוי <math>x</math> לבין משתנה תלוי <math>y</math>. בניגוד למצב הנפוץ בו הפתרון של משוואה הוא נקודה, במד״ר הפתרון הוא פונקציה. | משוואה דיפרנציאלית היא משוואה המקשרת בין משתנה בלתי תלוי <math>x</math> לבין משתנה תלוי <math>y</math>. בניגוד למצב הנפוץ בו הפתרון של משוואה הוא נקודה, במד״ר הפתרון הוא פונקציה. | ||
| שורה 13: | שורה 5: | ||
הצורה הכללית של משוואה דיפרנציאלית רגילה היא <math>F\Big(x,y(x),y'(x),\dots,y^{(n)}(x)\Big)=0</math> (<math>F</math> פונקציה ב־<math>n+2</math> משתנים). הצורה הכללית של משוואה דיפרנציאלית חלקית היא <math>F\left(x,y,z(x,y),\frac{\partial z}{\partial x},\frac{\partial z}{\partial y},\frac{\partial^2 z}{\partial x\partial y}\right)=0</math>. | הצורה הכללית של משוואה דיפרנציאלית רגילה היא <math>F\Big(x,y(x),y'(x),\dots,y^{(n)}(x)\Big)=0</math> (<math>F</math> פונקציה ב־<math>n+2</math> משתנים). הצורה הכללית של משוואה דיפרנציאלית חלקית היא <math>F\left(x,y,z(x,y),\frac{\partial z}{\partial x},\frac{\partial z}{\partial y},\frac{\partial^2 z}{\partial x\partial y}\right)=0</math>. | ||
| − | '''הגדרות:''' ''הסדר של מד״ר'' הוא דרגת הנגזרת הגבוהה ביותר במשוואה. ''המעלה'' היא החזקה של הנגזרת הגבוהה ביותר. | + | '''הגדרות:''' ''הסדר של מד״ר'' הוא דרגת הנגזרת הגבוהה ביותר במשוואה. ''המעלה'' היא החזקה של הנגזרת הגבוהה ביותר. נדגים: |
* <math>2xy'-3y=0</math>: הסדר הוא 1 והמעלה – 1. | * <math>2xy'-3y=0</math>: הסדר הוא 1 והמעלה – 1. | ||
* <math>2x^3y\left(\frac{\mathrm dy}{\mathrm dx}\right)^2-(1+x^3)=0</math>: הסדר הוא 1 והמעלה – 2. | * <math>2x^3y\left(\frac{\mathrm dy}{\mathrm dx}\right)^2-(1+x^3)=0</math>: הסדר הוא 1 והמעלה – 2. | ||
| שורה 21: | שורה 13: | ||
קיימות מד״ר שאנו כבר יודעים לפתור. למשל: | קיימות מד״ר שאנו כבר יודעים לפתור. למשל: | ||
* אם <math>y'={\mathrm e}^{2x}</math> אזי <math>y=\int {\mathrm e}^{2x}\mathrm dx=\frac{{\mathrm e}^{2x}}2+c</math>. | * אם <math>y'={\mathrm e}^{2x}</math> אזי <math>y=\int {\mathrm e}^{2x}\mathrm dx=\frac{{\mathrm e}^{2x}}2+c</math>. | ||
| − | * <math>\begin{align}&(y')^2+xy'+3=0\\\implies&y'=\frac{-x\pm\sqrt{x^2-12}}2\\\implies&y=\int\frac{-x\pm\sqrt{x^2-12}}2\mathrm dx=\dots\end{align}</math> | + | * {{left|<math>\begin{align}&(y')^2+xy'+3=0\\\implies&y'=\frac{-x\pm\sqrt{x^2-12}}2\\\implies&y=\int\frac{-x\pm\sqrt{x^2-12}}2\mathrm dx=\dots\end{align}</math>}} |
נשים לב שיש אינסוף פתרונות. | נשים לב שיש אינסוף פתרונות. | ||
| − | לא תמיד קל לפתור מד״ר: בהינתן <math>y'={\mathrm e}^{-x^2}</math> נקבל <math>y=\int {\mathrm e}^{-x^2}\mathrm dx</math>, והפתרון אינו אלמנטרי. למרות זאת, זה פתרון מפורט מספיק לצרכינו. נעיר שקיימת | + | לא תמיד קל לפתור מד״ר: בהינתן <math>y'={\mathrm e}^{-x^2}</math> נקבל <math>y=\int {\mathrm e}^{-x^2}\mathrm dx</math>, והפתרון אינו אלמנטרי. למרות זאת, זה פתרון מפורט מספיק לצרכינו. נעיר שקיימת פוקנציית השגיאה <math>\mbox{erf}</math> שעבורה <math>y=\frac\sqrt\pi2\mbox{erf}(x)+c</math>. |
| − | '''הגדרה:''' ''צורה נורמלית'' של מד״ר היא <math>y^{(n)}=f(x,y,y',\dots,y^{(n-1})</math> כאשר <math>n</math> סדר המשוואה. לפעמים קשה להגיע לצורה זו: לדוגמה, <math>y={\mathrm e}^{y'}+y'-x=0</math>. | + | '''הגדרה:''' ''צורה נורמלית'' של מד״ר היא <math>y^{(n)}=f(x,y,y',\dots,y^{(n-1)})</math> כאשר <math>n</math> סדר המשוואה. לפעמים קשה להגיע לצורה זו: לדוגמה, <math>y={\mathrm e}^{y'}+y'-x=0</math>. |
| − | + | ''הערה:'' <math>\equiv</math> מסמן שיוויון זהותי, כלומר שיוויון שמתקיים בכל נקודה. אם <math>f\equiv g</math> אז בפרט <math>f(x)=g(x)</math>, ולכן לא תמיד נקפיד לסמן ב־<math>\equiv</math> שיוויון זהותי. | |
| − | + | תהי <math>F(x,z_0,z_1,\dots,z_n)</math> פונקציה לינארית במשתנים <math>z_0,\dots,z_n</math>. אזי המד״ר המתאימה <math>F\left(x,y,y',\dots,y^{(n)}\right)=0</math> תקרא לינארית. <math>\sin(x)y''+x^2y'+3y-{\mathrm e}^{x^2}=0</math>, למשל. מד״ר לינארית מוצגת בצורה נורמלית כך: <math>y^{(n)}=\sum_{i=0}^{n-1}a_i(x)y^{(i)}+f(x)</math>. אם <math>f(x)\equiv0</math> אזי המד״ר נקראת "לינארית הומוגנית". דוגמה: <math>(y')^2+x^2+2=0</math>. | |
| − | '''הגדרה:''' ''פתרון כללי של מד״ר'' הוא משפחת פונקציות <math> | + | '''הגדרה:''' ''פתרון של מד״ר'' הוא פונקציה <math>\varphi(x)</math> כך שבהצבת <math>y=\varphi(x)</math> המד״ר הופכת לזהות <math>F(x,\varphi(x),\varphi'(x),\dots,\varphi^{(n)}(x))\equiv0</math>. דוגמה: <math>\varphi(x)=x^2</math> היא פתרון של <math>xy'-2y=0</math> מפני שבהצבה <math>y=\varphi(x)</math> נקבל <math>x(2x)-2x^2=0</math>, מה שמתקיים תמיד. |
| + | |||
| + | '''הגדרה:''' ''פתרון כללי של מד״ר'' הוא משפחת פונקציות <math>\varphi(x,c_1,\dots,c_n)</math> שכל אחת מהן פתרון התלוי ב־<math>n</math> פרמטרים וגזיר <math>n</math> פעמים לפי <math>x</math>. דוגמה:{{left|<math>\begin{align}&y''=x+1\\\implies&y'=\frac{x^2}2+x+c_1\\\implies&y=\frac{x^3}6+\frac{x^2}2+c_1x+c_2\end{align}</math>}}{{משל}} | ||
== מד״ר מסדר ראשון == | == מד״ר מסדר ראשון == | ||
'''הגדרה:''' ''מד״ר מסדר ראשון'' היא מד״ר מהצורה <math>F(x,y,y')=0</math>. באופן שקול, הצורה הנורמלית שלה היא <math>y'=f(x,y)</math>. דוגמאות:{{left| | '''הגדרה:''' ''מד״ר מסדר ראשון'' היא מד״ר מהצורה <math>F(x,y,y')=0</math>. באופן שקול, הצורה הנורמלית שלה היא <math>y'=f(x,y)</math>. דוגמאות:{{left| | ||
| − | + | # <math>xy'=x+y</math> | |
| − | + | # <math>\begin{align}&y'=\frac yx\end{align}</math> | |
| − | <math> | + | # <math>y'+x^2y=0</math>}} |
| − | + | מד״ר 2 שקולה ל־<math>\mathrm dy=\frac yx\mathrm dx</math> ומד״ר 3 שקולה ל־<math>\mathrm dy+x^2y\mathrm dx=0</math>. אלה הצורות הדיפרנציאליות. | |
=== בעיית קושי === | === בעיית קושי === | ||
| − | למצוא פתרון למד״ר <math>y'=f(x,y)</math> המקיים תנאי התחלה <math>y|_{x=x_0}=\varphi(x_0)=y_0</math>. | + | בכל הנוגע למד״ר מסדר ראשון, הבעיה היא למצוא פתרון למד״ר <math>y'=f(x,y)</math> המקיים תנאי התחלה <math>y|_{x=x_0}=\varphi(x_0)=y_0</math>. |
| − | + | === פתרון רגולרי וסינגולרי === | |
| + | '''הגדרות:''' בהנתן פתרון כללי של מד״ר <math>y=\varphi(x,c)</math>, פתרון המתקבל ע״י הצבת <math>c=c_0</math> מסוים נקרא ''פתרון פרטי'', ''רגולרי'' או ''רגיל''. פתרון שאינו מתקבל מ־<math>c</math> מסוים נקרא ''פתרון סינגולרי'' או ''מיוחד''. דוגמה: נתונה המד״ר <math>(y')^2=4y</math>. הפתרון הרגולרי הכללי הוא <math>y=(x+c)^2</math> לכל <math>c</math>, כגון <math>y=(x+3)^2</math>. <math>y=0</math> פתרון סינגולרי. | ||
| − | === משפט === | + | === משפט הקיום והיחידות === |
| − | נציג גרסה לא כ״כ פורמלית למשפט | + | נציג גרסה לא כ״כ פורמלית למשפט (את הגרסה המדויקת ואת ההוכחה נציג בהמשך). בהינתן מד״ר בצורה נורמלית <math>y'=f(x,y)</math>. אם הפונקציה <math>f</math> מקיימת את תנאי ליפשיץ במשתנה <math>y</math> בסביבה מסוימת של הנקודה <math>(x_0,y_0)</math> אזי קיימת סביבה שלה שבה למד״ר פתרון אחד ויחיד העובר ב־<math>(x_0,y_0)</math> (כלומר מקיים <math>y(x_0)=y_0</math>). |
| − | '''תזכורת:''' <math>f</math> מקיימת את תנאי ליפשיץ אם <math>\exists k:\ |f(x_1)-f(x_2)|\le k|x_1- | + | '''תזכורת:''' <math>f</math> מקיימת את תנאי ליפשיץ אם <math>\exists k:\ |f(x_1)-f(x_2)|\le k|x_1-x_2|</math>. |
=== מד״ר עם משתנים מופרדים === | === מד״ר עם משתנים מופרדים === | ||
| − | + | ==== דוגמה ==== | |
| + | נתון <math>2xy+y'=0</math>. אזי | ||
| + | {| | ||
| + | {{=|o= |r=\frac{y'}y=-2x |c=נניח <math>y\not\equiv0</math>:{{הפניה|ה-1|1}}}} | ||
| + | {{=|o=\implies |r=\frac{y'\mathrm dx}y=-2x\mathrm dx }} | ||
| + | {{=|o=\implies |r=\int\frac{\mathrm dy}y=-\int2x\mathrm dx }} | ||
| + | {{=|o=\implies |r=\ln\vert y\vert=-x^2+c_1 }} | ||
| + | {{=|o=\implies |r=\vert y\vert=c_2{\mathrm e}^{-x^2},\quad c_2>0 |c=נציב <math>c_2:={\mathrm e}^{c_1}</math>:}} | ||
| + | {{=|o=\implies |r=y=c{\mathrm e}^{-x^2},\quad c\ne0 |c=נציב <math>c:=c_2\sgn(y)</math>:{{הפניה|ה-2|2}}}} | ||
| + | |} | ||
| + | [[#ה-1-ref|^]] {{עוגן|ה-1|''הערה 1:''}} הנחנו ש־<math>y\not\equiv0</math> וחילקנו ב־<math>y</math>, אבל מה אם יש נקודות בודדות שבהן <math>y=0</math>? מקרה כזה אינו משנה לנו כיוון ש־<math>y</math> גזירה ובפרט רציפה, ולכן קיימים קטעים שבהם <math>y\ne0</math>. אנו יכולים לפתור את המד״ר בקטעים אלה ואז, הודות לרציפות, הפתרון ייתן את התוצאה הנכונה גם בנקודות שבהן <math>y=0</math>. | ||
| + | {{פס|[[#ה-2-ref|^]] {{עוגן|ה-2|''הערה 2:''}} הגדרנו <math>c=c_2\sgn(y)</math>, אך נשים לב ש־<math>c</math> מוכרח להיות קבוע. במקרה זה הדרישה הזאת מתקיימת: <math>\mathrm e^{-x^2}>0</math> לכל <math>x</math> ומכאן שלא קיימת נקודה שבה <math>y=0</math>. לפיכך, מפני ש־<math>y</math> רציפה, <math>y</math> אינה מחליפה סימן באף קטע, כלומר <math>\sgn(y)</math> קבוע. כך נקבל שגם <math>c</math> קבוע, כדרוש.}} | ||
| + | עתה נתייחס למקרה שבו <math>y\equiv0</math>. הצבה במד״ר תראה שזה פתרון ולבסוף הפתרון הכללי הוא <math>y=c{\mathrm e}^{-x^2},\quad c\in\mathbb R</math>. {{משל}} | ||
| + | |||
| + | נוכל להכליל את הדוגמה למקרה כללי: אם <math>y'=f(x)g(y)</math> אזי <math>\int\frac{\mathrm dy}{g(y)}=\int f(x)\mathrm dx</math>. | ||
| + | |||
| + | ==== צורה כללית ==== | ||
| + | |||
| + | הצורה הכללית של מד״ר מסדר ראשון עם משתנים מופרדים בכתיב דיפרנציאלי: <math>M_1(x)N_1(y)\mathrm dx+M_2(x)N_2(y)\mathrm dy=0</math>. אם <math>N_1(y_0)=0</math> עבור <math>y_0</math> כלשהו אזי <math>y(x)\equiv y_0</math> פותר את המד״ר. אם <math>M_2(x_0)=0</math> עבור <math>x_0</math> כלשהו אזי <math>x(y)\equiv x_0</math> פתרון (במובן כלשהו – רגולרי או סינגולרי). אם <math>N_1(y)M_2(x)\ne0</math> נחלק בהם ונקבל <math>\int\frac{M_1(x)}{M_2(x)}\mathrm dx+\int\frac{N_2(y)}{N_1(y)}\mathrm dy=c</math>. | ||
| − | + | ===== דוגמה ===== | |
| + | <math>x^2y^2y'=y-1</math>. נמיר זאת לכתיב דיפרנציאלי ונקבל <math>x^2y^2\mathrm dy+(1-y)\mathrm dx=0</math>. הפתרונות הם <math>y=1</math> או <math>x=0</math> או <math>\frac{\mathrm dx}{x^2}+\frac{y^2}{1-y}\mathrm dy=0</math>. במקרה האחרון <math>-\frac1x=\int\frac{(y-1)(y+1)+1}{y-1}\mathrm dy=\frac{y^2}2+y+\ln|y-1|+c_1</math>. לא נצליח לחלץ את <math>y</math>, אבל נוכל לחלץ את <math>x</math>: <math>x=\frac1{c-y^2/2-y-\ln|y-1|}</math> (כאשר <math>c=-c_1</math>). {{משל}} | ||
=== מד״ר פתורות ע״י הפרדת משתנים === | === מד״ר פתורות ע״י הפרדת משתנים === | ||
| − | <math>y'=f(ax+by)</math>. נגדיר <math>z=ax+by</math>, לכן <math>z'=a+by'</math> | + | נתונה מד״ר מהצורה <math>y'=f(ax+by)</math>. נגדיר <math>z=ax+by</math>, לכן <math>z'=a+by'</math> ולפיכך {{left|<math>\begin{align}&z'=a+bf(z)\\\implies&\frac{z'}{bf(z)+a}=1\\\implies&\underbrace{\int\frac{\mathrm dz}{bf(z)+a}}_{g(z)}=x+c\end{align}</math>}} |
| + | לכן <math>g(ax+by)=x+c</math> ואם <math>g</math> הפיכה אזי <math>y=\frac{g^{-1}(x+c)-ax}b</math>. | ||
| − | + | ==== דוגמה ==== | |
| + | <math>y'=\frac{1-x+y}{x-y}</math>. אזי עבור <math>z=x-y</math> נקבל | ||
| + | {| | ||
| + | {{=|o= |r=z'=1-y'=\frac{2z-1}z }} | ||
| + | {{=|o=\implies |r=\frac{zz'}{2z-1}=1 |c=נניח <math>z\not\equiv\frac12</math>:}} | ||
| + | {{=|o=\implies |r=\int\frac z{2z-1}\mathrm dz=\int\mathrm dx }} | ||
| + | {{=|o=\implies |r=\int\left(\frac12+\frac12\frac1{2z-1}\right)\mathrm dz=x+c }} | ||
| + | {{=|o=\implies |r=\frac z2+\frac14\ln\left\vert z-\frac12\right\vert=x+c}} | ||
| + | {{=|o=\implies |r=\frac{x-y}2+\frac14\ln\left\vert x-y-\frac12\right\vert=x+c }} | ||
| + | |} | ||
| + | הצבת <math>z\equiv\frac12</math> נותנת <math>y'=\frac{1-\frac12}{1/2}=1</math> ולכן <math>y=x+\frac12</math> פתרון. {{משל}} | ||
| + | === הומוגניות === | ||
| + | '''הגדרה:''' פונקציה <math>f(x,y)</math> נקראת ''הומוגנית מסדר <math>k</math>'' אם לכל <math>\lambda>0</math> מתקיים <math>f(\lambda x,\lambda y)=\lambda^k f(x,y)</math>. למשל: | ||
| + | * <math>f(x,y)=\frac{x-y}{x+y}</math> הומוגנית מסדר 0 כי <math>f(\lambda x,\lambda y)=\frac{\lambda x-\lambda y}{\lambda x+\lambda y}=\frac{x-y}{x+y}=\lambda^0f(x,y)</math>. | ||
| + | * <math>f(x,y)=x^2+3y^2+8xy</math> הומוגנית מסדר 2 כי <math>f(\lambda x,\lambda y)=\lambda^2x^2+3\lambda^2y^2+8\lambda^2xy=\lambda^2f(x,y)</math>. | ||
| − | === | + | ==== משפט ==== |
| − | פונקציה <math>f(x,y)</math> | + | פונקציה <math>f(x,y)</math> ניתנת לכתיבה בצורה <math>f(x,y)=\varphi\left(\frac yx\right)</math> לכל <math>x\ne0</math> אם״ם היא הומוגנית מסדר 0. |
| − | + | ===== הוכחה ===== | |
| − | + | <math>\Longleftarrow</math>: <math>f(\lambda x,\lambda y)=\varphi\left(\frac{\lambda y}{\lambda x}\right)=\varphi\left(\frac yx\right)=f(x,y)</math>. | |
| − | + | ||
| − | == | + | <math>\implies</math>: נתון <math>f(\lambda x,\lambda y)=f(x,y)</math>. אם <math>x>0</math> נבחר <math>\lambda=\frac1x</math> ולכן <math>f(x,y)=f(\lambda x,\lambda y)=f\left(1,\frac yx\right)=\varphi_1\left(\frac yx\right)</math>. במקרה <math>x<0</math> נציב <math>\lambda=-\frac1x</math>, ואז <math>f(x,y)=f\left(-1,-\frac yx\right)=\varphi_2\left(\frac yx\right)</math>. {{משל}} |
| − | + | ||
| − | ==== | + | ==== מד״ר הומוגנית ==== |
| − | + | '''הגדרה:''' אם ניתן לכתוב את המד״ר בצורה <math>y'=g\left(\frac yx\right)</math> אזי היא נקראת ''הומוגנית''. | |
| − | <math> | + | |
| − | + | ניתן לפתור כל מד״ר הומוגנית באמצאות ההצבה <math>z=\frac yx</math>: מתקיים <math>g(z)=y'=(zx)'=z'x+z</math> ולכן אם <math>z\not\equiv g(z)</math> אז | |
| + | {{left|<math>\begin{align}&g(z)-z=xz'\\\implies&\int\frac{\mathrm dz}{g(z)-z}=\int\frac{\mathrm dx}x\end{align}</math>}} | ||
| + | עבור <math>h(z)</math> המוגדרת כאגף שמאל, <math>h(z)=h\left(\frac yx\right)=\ln|x|+c</math>. במידה ו־<math>h</math> הפיכה <math>y=xh^{-1}(\ln|x|+c)</math>. | ||
| − | + | ===== תרגיל ===== | |
| + | פתרו <math>xy'=x+y</math> עם תנאי ההתחלה <math>y(3)=8</math>. | ||
| − | + | ====== פתרון ====== | |
| + | בנקודות <math>x\ne0</math> נקבל <math>y'=1+\frac yx=1+z</math>. בנוסף, {{left|<math>\begin{align}&y=zx\\\implies&y'=(zx)'=z'x+z\\\implies&z'x=z-(1+z)=1\\\implies&\int z'\mathrm dx=\int\frac{\mathrm dx}x\\\implies&z=\ln|x|+c_1\\\implies&y=xz=x(\ln|x|+c_1)\end{align}</math>}} נסמן <math>c={\mathrm e}^{c_1}</math> ולפיכך <math>y=x\ln|cx|,\quad c>0</math>. אם נציב את תנאי ההתחלה נקבל <math>8=y(3)=3\ln|c\cdot3|</math> ולפיכן <math>c=\frac{\mathrm e^{8/3}}3</math>. לסיכום, <math>y=x\ln\left|\frac{\mathrm e^{8/3}}3x\right|</math>. {{משל}} | ||
גרסה מ־16:42, 3 באוגוסט 2012
תוכן עניינים
מבוא
משוואה דיפרנציאלית היא משוואה המקשרת בין משתנה בלתי תלוי 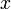 לבין משתנה תלוי
לבין משתנה תלוי 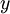 . בניגוד למצב הנפוץ בו הפתרון של משוואה הוא נקודה, במד״ר הפתרון הוא פונקציה.
. בניגוד למצב הנפוץ בו הפתרון של משוואה הוא נקודה, במד״ר הפתרון הוא פונקציה.
הצורה הכללית של משוואה דיפרנציאלית רגילה היא 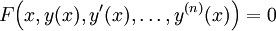 (
(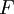 פונקציה ב־
פונקציה ב־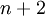 משתנים). הצורה הכללית של משוואה דיפרנציאלית חלקית היא
משתנים). הצורה הכללית של משוואה דיפרנציאלית חלקית היא 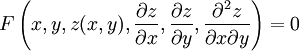 .
.
הגדרות: הסדר של מד״ר הוא דרגת הנגזרת הגבוהה ביותר במשוואה. המעלה היא החזקה של הנגזרת הגבוהה ביותר. נדגים:
-
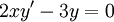 : הסדר הוא 1 והמעלה – 1.
: הסדר הוא 1 והמעלה – 1. -
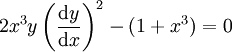 : הסדר הוא 1 והמעלה – 2.
: הסדר הוא 1 והמעלה – 2. -
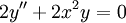 : הסדר הוא 2 והמעלה – 1.
: הסדר הוא 2 והמעלה – 1. -
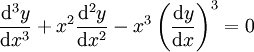 : הסדר הוא 3 והמעלה – 1.
: הסדר הוא 3 והמעלה – 1.
קיימות מד״ר שאנו כבר יודעים לפתור. למשל:
- אם
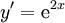 אזי
אזי 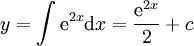 .
. -
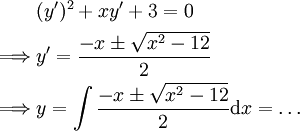
נשים לב שיש אינסוף פתרונות.
לא תמיד קל לפתור מד״ר: בהינתן 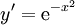 נקבל
נקבל 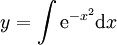 , והפתרון אינו אלמנטרי. למרות זאת, זה פתרון מפורט מספיק לצרכינו. נעיר שקיימת פוקנציית השגיאה
, והפתרון אינו אלמנטרי. למרות זאת, זה פתרון מפורט מספיק לצרכינו. נעיר שקיימת פוקנציית השגיאה 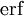 שעבורה
שעבורה 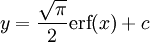 .
.
הגדרה: צורה נורמלית של מד״ר היא 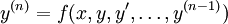 כאשר
כאשר  סדר המשוואה. לפעמים קשה להגיע לצורה זו: לדוגמה,
סדר המשוואה. לפעמים קשה להגיע לצורה זו: לדוגמה, 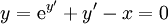 .
.
הערה:  מסמן שיוויון זהותי, כלומר שיוויון שמתקיים בכל נקודה. אם
מסמן שיוויון זהותי, כלומר שיוויון שמתקיים בכל נקודה. אם 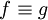 אז בפרט
אז בפרט 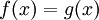 , ולכן לא תמיד נקפיד לסמן ב־
, ולכן לא תמיד נקפיד לסמן ב־ שיוויון זהותי.
שיוויון זהותי.
תהי 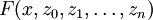 פונקציה לינארית במשתנים
פונקציה לינארית במשתנים 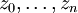 . אזי המד״ר המתאימה
. אזי המד״ר המתאימה 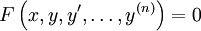 תקרא לינארית.
תקרא לינארית. 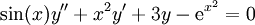 , למשל. מד״ר לינארית מוצגת בצורה נורמלית כך:
, למשל. מד״ר לינארית מוצגת בצורה נורמלית כך: 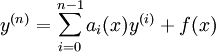 . אם
. אם 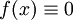 אזי המד״ר נקראת "לינארית הומוגנית". דוגמה:
אזי המד״ר נקראת "לינארית הומוגנית". דוגמה: 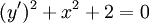 .
.
הגדרה: פתרון של מד״ר הוא פונקציה 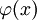 כך שבהצבת
כך שבהצבת 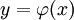 המד״ר הופכת לזהות
המד״ר הופכת לזהות 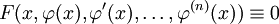 . דוגמה:
. דוגמה: 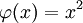 היא פתרון של
היא פתרון של 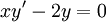 מפני שבהצבה
מפני שבהצבה 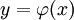 נקבל
נקבל 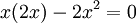 , מה שמתקיים תמיד.
, מה שמתקיים תמיד.
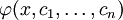 שכל אחת מהן פתרון התלוי ב־
שכל אחת מהן פתרון התלוי ב־ פרמטרים וגזיר
פרמטרים וגזיר  פעמים לפי
פעמים לפי 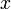 . דוגמה:
. דוגמה: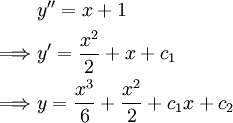

מד״ר מסדר ראשון
הגדרה: מד״ר מסדר ראשון היא מד״ר מהצורה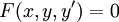 . באופן שקול, הצורה הנורמלית שלה היא
. באופן שקול, הצורה הנורמלית שלה היא 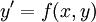 . דוגמאות:
. דוגמאות:מד״ר 2 שקולה ל־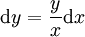 ומד״ר 3 שקולה ל־
ומד״ר 3 שקולה ל־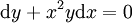 . אלה הצורות הדיפרנציאליות.
. אלה הצורות הדיפרנציאליות.
בעיית קושי
בכל הנוגע למד״ר מסדר ראשון, הבעיה היא למצוא פתרון למד״ר 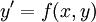 המקיים תנאי התחלה
המקיים תנאי התחלה 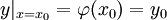 .
.
פתרון רגולרי וסינגולרי
הגדרות: בהנתן פתרון כללי של מד״ר 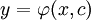 , פתרון המתקבל ע״י הצבת
, פתרון המתקבל ע״י הצבת 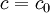 מסוים נקרא פתרון פרטי, רגולרי או רגיל. פתרון שאינו מתקבל מ־
מסוים נקרא פתרון פרטי, רגולרי או רגיל. פתרון שאינו מתקבל מ־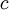 מסוים נקרא פתרון סינגולרי או מיוחד. דוגמה: נתונה המד״ר
מסוים נקרא פתרון סינגולרי או מיוחד. דוגמה: נתונה המד״ר 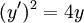 . הפתרון הרגולרי הכללי הוא
. הפתרון הרגולרי הכללי הוא 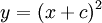 לכל
לכל 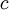 , כגון
, כגון  .
. 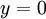 פתרון סינגולרי.
פתרון סינגולרי.
משפט הקיום והיחידות
נציג גרסה לא כ״כ פורמלית למשפט (את הגרסה המדויקת ואת ההוכחה נציג בהמשך). בהינתן מד״ר בצורה נורמלית 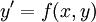 . אם הפונקציה
. אם הפונקציה 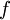 מקיימת את תנאי ליפשיץ במשתנה
מקיימת את תנאי ליפשיץ במשתנה 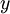 בסביבה מסוימת של הנקודה
בסביבה מסוימת של הנקודה 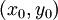 אזי קיימת סביבה שלה שבה למד״ר פתרון אחד ויחיד העובר ב־
אזי קיימת סביבה שלה שבה למד״ר פתרון אחד ויחיד העובר ב־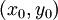 (כלומר מקיים
(כלומר מקיים 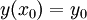 ).
).
תזכורת: 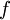 מקיימת את תנאי ליפשיץ אם
מקיימת את תנאי ליפשיץ אם 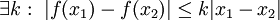 .
.
מד״ר עם משתנים מופרדים
דוגמה
נתון 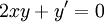 . אזי
. אזי
נניח 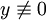 :[1] :[1]
|
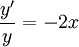
|
|||||
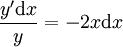
|
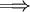
|
|||||
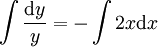
|
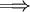
|
|||||
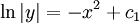
|
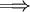
|
|||||
נציב 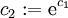 : :
|
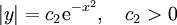
|
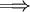
|
||||
נציב 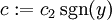 :[2] :[2]
|
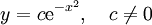
|
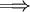
|
^ הערה 1: הנחנו ש־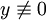 וחילקנו ב־
וחילקנו ב־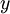 , אבל מה אם יש נקודות בודדות שבהן
, אבל מה אם יש נקודות בודדות שבהן 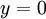 ? מקרה כזה אינו משנה לנו כיוון ש־
? מקרה כזה אינו משנה לנו כיוון ש־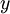 גזירה ובפרט רציפה, ולכן קיימים קטעים שבהם
גזירה ובפרט רציפה, ולכן קיימים קטעים שבהם 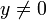 . אנו יכולים לפתור את המד״ר בקטעים אלה ואז, הודות לרציפות, הפתרון ייתן את התוצאה הנכונה גם בנקודות שבהן
. אנו יכולים לפתור את המד״ר בקטעים אלה ואז, הודות לרציפות, הפתרון ייתן את התוצאה הנכונה גם בנקודות שבהן 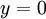 .
.
^ הערה 2: הגדרנו 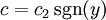 , אך נשים לב ש־
, אך נשים לב ש־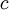 מוכרח להיות קבוע. במקרה זה הדרישה הזאת מתקיימת:
מוכרח להיות קבוע. במקרה זה הדרישה הזאת מתקיימת: 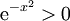 לכל
לכל 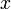 ומכאן שלא קיימת נקודה שבה
ומכאן שלא קיימת נקודה שבה 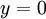 . לפיכך, מפני ש־
. לפיכך, מפני ש־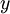 רציפה,
רציפה, 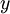 אינה מחליפה סימן באף קטע, כלומר
אינה מחליפה סימן באף קטע, כלומר 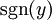 קבוע. כך נקבל שגם
קבוע. כך נקבל שגם 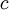 קבוע, כדרוש.
קבוע, כדרוש.
עתה נתייחס למקרה שבו 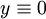 . הצבה במד״ר תראה שזה פתרון ולבסוף הפתרון הכללי הוא
. הצבה במד״ר תראה שזה פתרון ולבסוף הפתרון הכללי הוא 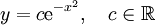 .
. 
נוכל להכליל את הדוגמה למקרה כללי: אם 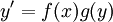 אזי
אזי 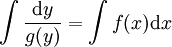 .
.
צורה כללית
הצורה הכללית של מד״ר מסדר ראשון עם משתנים מופרדים בכתיב דיפרנציאלי: 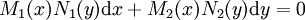 . אם
. אם 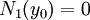 עבור
עבור 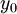 כלשהו אזי
כלשהו אזי 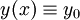 פותר את המד״ר. אם
פותר את המד״ר. אם 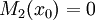 עבור
עבור 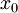 כלשהו אזי
כלשהו אזי 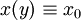 פתרון (במובן כלשהו – רגולרי או סינגולרי). אם
פתרון (במובן כלשהו – רגולרי או סינגולרי). אם 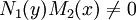 נחלק בהם ונקבל
נחלק בהם ונקבל 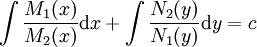 .
.
דוגמה
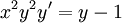 . נמיר זאת לכתיב דיפרנציאלי ונקבל
. נמיר זאת לכתיב דיפרנציאלי ונקבל 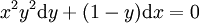 . הפתרונות הם
. הפתרונות הם 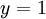 או
או 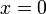 או
או 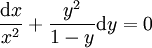 . במקרה האחרון
. במקרה האחרון 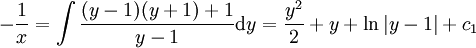 . לא נצליח לחלץ את
. לא נצליח לחלץ את 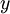 , אבל נוכל לחלץ את
, אבל נוכל לחלץ את 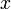 :
: 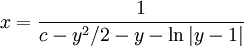 (כאשר
(כאשר 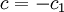 ).
). 
מד״ר פתורות ע״י הפרדת משתנים
נתונה מד״ר מהצורה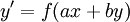 . נגדיר
. נגדיר 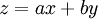 , לכן
, לכן 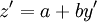 ולפיכך
ולפיכך 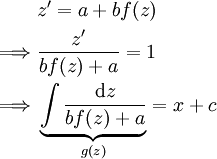
לכן 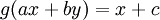 ואם
ואם 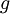 הפיכה אזי
הפיכה אזי 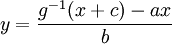 .
.
דוגמה
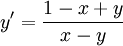 . אזי עבור
. אזי עבור 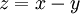 נקבל
נקבל
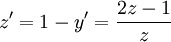
|
||||||
נניח 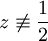 : :
|
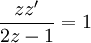
|
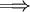
|
||||
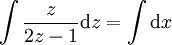
|
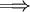
|
|||||
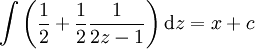
|
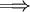
|
|||||
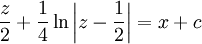
|
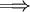
|
|||||
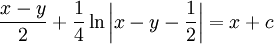
|
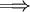
|
הצבת 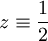 נותנת
נותנת 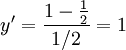 ולכן
ולכן 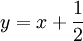 פתרון.
פתרון. 
הומוגניות
הגדרה: פונקציה 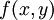 נקראת הומוגנית מסדר
נקראת הומוגנית מסדר 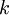 אם לכל
אם לכל 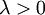 מתקיים
מתקיים 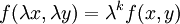 . למשל:
. למשל:
-
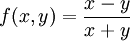 הומוגנית מסדר 0 כי
הומוגנית מסדר 0 כי 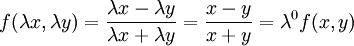 .
. -
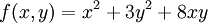 הומוגנית מסדר 2 כי
הומוגנית מסדר 2 כי 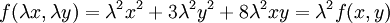 .
.
משפט
פונקציה 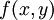 ניתנת לכתיבה בצורה
ניתנת לכתיבה בצורה 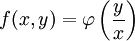 לכל
לכל 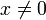 אם״ם היא הומוגנית מסדר 0.
אם״ם היא הומוגנית מסדר 0.
הוכחה
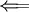 :
: 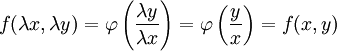 .
.
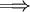 : נתון
: נתון 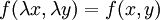 . אם
. אם 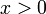 נבחר
נבחר 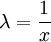 ולכן
ולכן 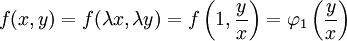 . במקרה
. במקרה 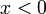 נציב
נציב 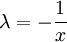 , ואז
, ואז 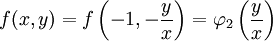 .
. 
מד״ר הומוגנית
הגדרה: אם ניתן לכתוב את המד״ר בצורה 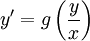 אזי היא נקראת הומוגנית.
אזי היא נקראת הומוגנית.
ניתן לפתור כל מד״ר הומוגנית באמצאות ההצבה 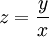 : מתקיים
: מתקיים 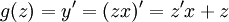 ולכן אם
ולכן אם 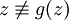 אז
אז
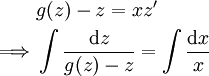
עבור 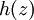 המוגדרת כאגף שמאל,
המוגדרת כאגף שמאל, 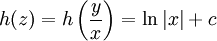 . במידה ו־
. במידה ו־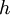 הפיכה
הפיכה 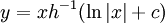 .
.
תרגיל
פתרו 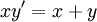 עם תנאי ההתחלה
עם תנאי ההתחלה 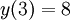 .
.
פתרון
בנקודות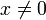 נקבל
נקבל 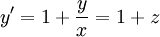 . בנוסף,
. בנוסף, 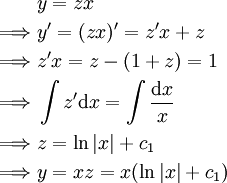
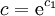 ולפיכך
ולפיכך 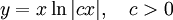 . אם נציב את תנאי ההתחלה נקבל
. אם נציב את תנאי ההתחלה נקבל 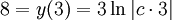 ולפיכן
ולפיכן 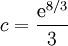 . לסיכום,
. לסיכום, 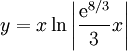 .
.