מדר קיץ תשעב/סיכומים/הרצאות/30.7.12
מרצה: ראובן כהן, reuven (@) math.biu.ac.il
u.math.biu.ac.il/~reuven/ode.pdf
050-5217779
תוכן עניינים
מבוא
משוואה דיפרנציאלית היא משוואה המקשרת בין משתנה בלתי תלוי  לבין משתנה תלוי
לבין משתנה תלוי  . בניגוד למצב הנפוץ בו הפתרון של משוואה הוא נקודה, במד״ר הפתרון הוא פונקציה.
. בניגוד למצב הנפוץ בו הפתרון של משוואה הוא נקודה, במד״ר הפתרון הוא פונקציה.
הצורה הכללית של משוואה דיפרנציאלית רגילה היא 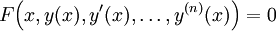 (
( פונקציה ב־
פונקציה ב־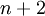 משתנים). הצורה הכללית של משוואה דיפרנציאלית חלקית היא
משתנים). הצורה הכללית של משוואה דיפרנציאלית חלקית היא 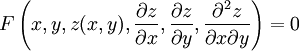 .
.
הגדרות: הסדר של מד״ר הוא דרגת הנגזרת הגבוהה ביותר במשוואה. המעלה היא החזקה של הנגזרת הגבוהה ביותר. דוגמאות:
-
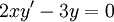 : הסדר הוא 1 והמעלה – 1.
: הסדר הוא 1 והמעלה – 1. -
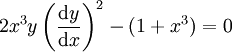 : הסדר הוא 1 והמעלה – 2.
: הסדר הוא 1 והמעלה – 2. -
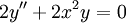 : הסדר הוא 2 והמעלה – 1.
: הסדר הוא 2 והמעלה – 1. -
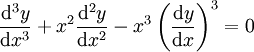 : הסדר הוא 3 והמעלה – 1.
: הסדר הוא 3 והמעלה – 1.
קיימות מד״ר שאנו כבר יודעים לפתור. למשל:
- אם
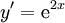 אזי
אזי 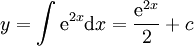 .
. -
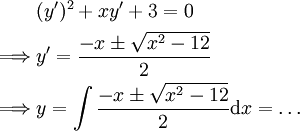
נשים לב שיש אינסוף פתרונות.
לא תמיד קל לפתור מד״ר: בהינתן 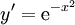 נקבל
נקבל 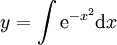 , והפתרון אינו אלמנטרי. למרות זאת, זה פתרון מפורט מספיק לצרכינו. נעיר שקיימת פוקנציה
, והפתרון אינו אלמנטרי. למרות זאת, זה פתרון מפורט מספיק לצרכינו. נעיר שקיימת פוקנציה 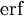 שעבורה
שעבורה 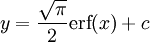 .
.
הגדרה: צורה נורמלית של מד״ר היא 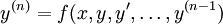 כאשר
כאשר  סדר המשוואה. לפעמים קשה להגיע לצורה זו: לדוגמה,
סדר המשוואה. לפעמים קשה להגיע לצורה זו: לדוגמה, 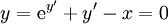 .
.
תהי 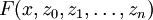 פונקציה לינארית במשתנים
פונקציה לינארית במשתנים 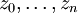 . אזי המד״ר המתאימה תקרא לינארית. לדוגמה:
. אזי המד״ר המתאימה תקרא לינארית. לדוגמה: 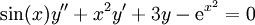 . מד״ר לינארית מוצגת בצורה נורמלית כך:
. מד״ר לינארית מוצגת בצורה נורמלית כך: 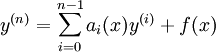 . אם
. אם 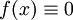 אזי המד״ר נקראת "לינארית הומוגנית". דוגמה:
אזי המד״ר נקראת "לינארית הומוגנית". דוגמה: 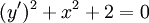 .
.
הגדרה: פתרון של מד״ר הוא פונקציה 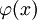 כך שבהצבת
כך שבהצבת 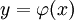 המד״ר הופכת לזהות
המד״ר הופכת לזהות 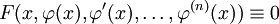 . דוגמה:
. דוגמה: 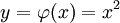 היא פתרון של
היא פתרון של 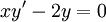 מפני שבהצבה
מפני שבהצבה 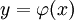 נקבל
נקבל 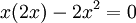 , מה שמתקיים תמיד.
, מה שמתקיים תמיד.
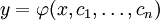 התלויות ב־
התלויות ב־ פרמטרים וגזירות
פרמטרים וגזירות  פעמים לפי x. דוגמה:
פעמים לפי x. דוגמה: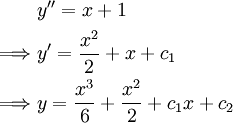
מד״ר מסדר ראשון
הגדרה: מד״ר מסדר ראשון היא מד״ר מהצורה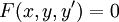 . באופן שקול, הצורה הנורמלית שלה היא
. באופן שקול, הצורה הנורמלית שלה היא 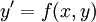 . דוגמאות:
. דוגמאות: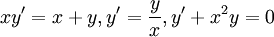 . לגבי המשוואה האחרונה:
. לגבי המשוואה האחרונה: 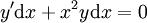 ולכן
ולכן 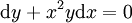 . זו הצורה הדיפרנציאלית. לגבי המשוואה השנייה:
. זו הצורה הדיפרנציאלית. לגבי המשוואה השנייה: 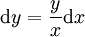 .
.
בעיית קושי
למצוא פתרון למד״ר 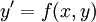 המקיים תנאי התחלה
המקיים תנאי התחלה 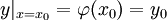 .
.
פתרון רגולרי וסינגולרי: בהנתן פתרון כללי של מד״ר 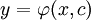 , פתרון המתקבל ע״י הצבת
, פתרון המתקבל ע״י הצבת 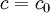 מסוים נקרא פתרון פרטי, רגולרי או רגיל. פתרון שאינו מתקבל מ־c מסוים נקרא פתרון סינגולרי או מיוחד. דוגמה:
מסוים נקרא פתרון פרטי, רגולרי או רגיל. פתרון שאינו מתקבל מ־c מסוים נקרא פתרון סינגולרי או מיוחד. דוגמה: 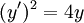 . הפתרון הכללי הוא
. הפתרון הכללי הוא 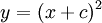 לכל c. לדוגמה
לכל c. לדוגמה 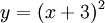 הוא פתרון רגולרי, ו־
הוא פתרון רגולרי, ו־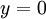 פתרון סינגולרי.
פתרון סינגולרי.
משפט
נציג גרסה לא כ״כ פורמלית למשפט הקיום והיחידות. את הגרסה המדוייקת ואת ההוכחה נציג בשיעור הבא. בהינתן מד״ר בצורה נורמלית 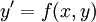 . אם הפונקציה
. אם הפונקציה  מקיימת את תנאי ליפשיץ במשנתנה
מקיימת את תנאי ליפשיץ במשנתנה  בסביבה מסויימת של הנקודה
בסביבה מסויימת של הנקודה 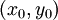 אזי קיימת סביבה שלה
אזי קיימת סביבה שלה 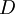 שבה המד״ר פתרון אחד ויחיד העובר ב־
שבה המד״ר פתרון אחד ויחיד העובר ב־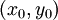 (כלומר מקיים
(כלומר מקיים 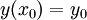 ).
).
תזכורת:  מקיימת את תנאי ליפשיץ אם
מקיימת את תנאי ליפשיץ אם 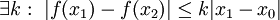 .
.
מד״ר עם משתנים מופרדים
דוגמה: 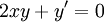 . אם
. אם 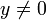 אז
אז 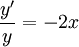 . מכאן ש־
. מכאן ש־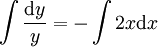 ולפיכך
ולפיכך 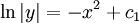 . נסמן
. נסמן 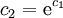 ונקבל
ונקבל 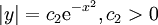 ולפיכך (עבור
ולפיכך (עבור 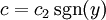 )
) 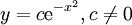 . נשים לב שבפתרון התעלמנו מהמקרה
. נשים לב שבפתרון התעלמנו מהמקרה 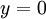 ולבסוף הפתרון הסופי הוא
ולבסוף הפתרון הסופי הוא 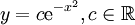 . מקרה כללי: אם
. מקרה כללי: אם 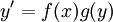 אזי
אזי 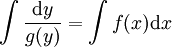 .
.
הצורה הכללית של מד״ר עם משתנים מופרדים בכתיב דיפרנציאלי: 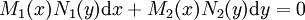 . אם
. אם 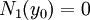 עבור
עבור 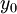 כלשהו אזי
כלשהו אזי 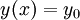 פותר את המד״ר. אם
פותר את המד״ר. אם 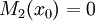 עבור
עבור  כלשהו אזי
כלשהו אזי 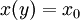 פתרון (במובן כלשהו). אם
פתרון (במובן כלשהו). אם 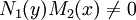 נחלק בהם ונקבל
נחלק בהם ונקבל 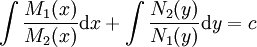 . דוגמה:
. דוגמה: 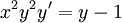 . בכתיב דיפרנציאלי
. בכתיב דיפרנציאלי 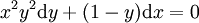 פתרונות:
פתרונות: 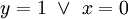 או
או 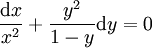 . לכן
. לכן 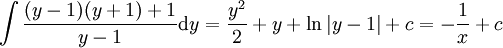 . לא נצליח לחלץ את
. לא נצליח לחלץ את  , אבל נוכל לחלץ את
, אבל נוכל לחלץ את  :
: 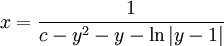 .
.
מד״ר פתורות ע״י הפרדת משתנים
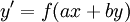 . נגדיר
. נגדיר 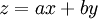 , לכן
, לכן 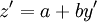 כלומר
כלומר 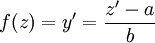 ולכן
ולכן 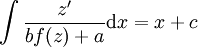 . נסמן את אגף שמאל כ־
. נסמן את אגף שמאל כ־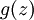 ולכן
ולכן 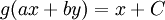 ואם
ואם  הפיכה אזי
הפיכה אזי 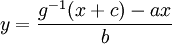 .
.
דוגמה: 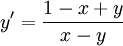 . אזי עבור
. אזי עבור 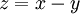 נקבל
נקבל 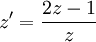 . לפיכך
. לפיכך 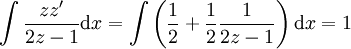 . מכאן ש־
. מכאן ש־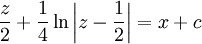 ולבסוף:
ולבסוף: 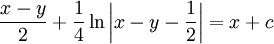 .
.
מד״ר הומוגנית
פונקציה 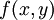 נקראת הומוגנית מסדר
נקראת הומוגנית מסדר  אם לכל
אם לכל 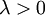 מתקיים
מתקיים 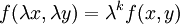 .
.
דוגמאות:
-
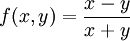 הומוגנית מסדר 0.
הומוגנית מסדר 0. -
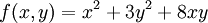 הומוגנית מסדר 2.
הומוגנית מסדר 2.
משפט
פונקציה 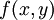 ניתנת לכתיבה בצורה
ניתנת לכתיבה בצורה 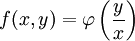 אם״ם היא הומוגנית מסדר 0.
אם״ם היא הומוגנית מסדר 0.
הוכחה
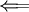 : טריוויאלי.
: טריוויאלי.
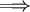 : נתון
: נתון 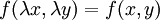 . נבחר
. נבחר 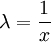 (כאשר
(כאשר 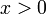 ) ולכן
) ולכן 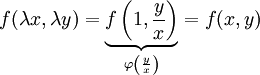 . במקרה
. במקרה 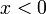 נציב
נציב 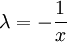 .
.
הגדרה: אם ניתן לכתוב את המד״ר בצורה 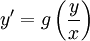 אזי היא נקראת הומוגנית.
אזי היא נקראת הומוגנית.
דוגמה: 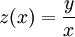 לכן
לכן 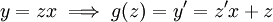 . אזי
. אזי 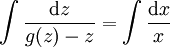 ולפיכך, עבור
ולפיכך, עבור 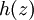 המוגדרת כאגף שמאל,
המוגדרת כאגף שמאל, 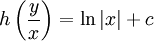 ואז
ואז 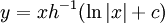 אם
אם 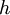 הפיכה.
הפיכה.
דוגמה: 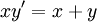 . אם
. אם 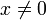 נקבל
נקבל 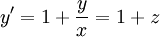 ואז
ואז 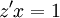 . לבסוף
. לבסוף 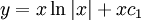 . נסמן
. נסמן 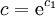 ולפיכך
ולפיכך 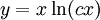 . נתונים תנאי ההתחלה
. נתונים תנאי ההתחלה 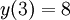 אזי
אזי 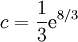 .
.