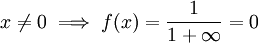משתמש:אור שחף/133 - תרגול/8.5.11
תוכן עניינים
אינטגרל
דוגמה 1
ראינו בשיעור שעבר כי 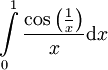 מתכנס לפי דיריכלה. נראה שלא מתכנס בהחלט.
מתכנס לפי דיריכלה. נראה שלא מתכנס בהחלט.
פתרון
ברור כי 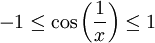 ולכן
ולכן 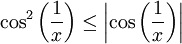 . מספיק להסתכל על
. מספיק להסתכל על 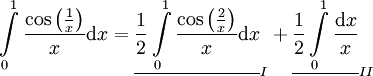 . ברור שאינטגרל II מתבדר, ולכן אם אינטגרל I מתכנס אז סיימנו את ההוכחה: נציב עיבוד הנוסחה נכשל (פונקציה \frahttp לא מוכרת): y=\frahttp://www.math-wiki.com/skins/common/images/button_math.pngc2x
. ברור שאינטגרל II מתבדר, ולכן אם אינטגרל I מתכנס אז סיימנו את ההוכחה: נציב עיבוד הנוסחה נכשל (פונקציה \frahttp לא מוכרת): y=\frahttp://www.math-wiki.com/skins/common/images/button_math.pngc2x
ואזנקבל
שמתכנס לפי דיריכלה.

דוגמה 2
קבעו האם 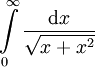 מתכנס או מתבדר.
מתכנס או מתבדר.
פתרון
נחלק לשני אינטגרלים 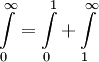 עבור
עבור ![x\in(0,1]](/images/math/f/e/e/fee569b4d135be6dd93b57b0a02a99d5.png)
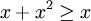 , לכן
, לכן 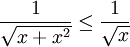 . ברור ש-
. ברור ש-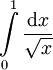 מתכנס ולכן לפי מבחן ההשוואה
מתכנס ולכן לפי מבחן ההשוואה 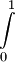 מתכנס.
מתכנס.
עבור 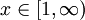
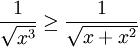 שוב נסכל על
שוב נסכל על 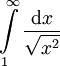 ולכן גם כן מתכנס לפי מבחן ההשוואה. לסיכום האינטגרל מתכנס.
ולכן גם כן מתכנס לפי מבחן ההשוואה. לסיכום האינטגרל מתכנס. 
נושא שני:
התכנסות של פונקציות
לדוגמה נתבונן בסדרת הפונקציות 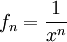 . קל לראות שאת סדרת הפונקציות ניתן לרשום כ-
. קל לראות שאת סדרת הפונקציות ניתן לרשום כ-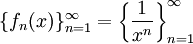 . לדגמה, נבחר
. לדגמה, נבחר 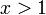 . קל לראות ש-
. קל לראות ש-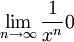 , ולכן
, ולכן 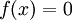 היא פונקצית הגבול.
היא פונקצית הגבול.
הגדרות
- סדרה
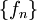 של פונקציות היא התאמה שבה לכל n טבעי מותאמת פונקציה
של פונקציות היא התאמה שבה לכל n טבעי מותאמת פונקציה  .
. - אם לכל
 בקטע הסדרה
בקטע הסדרה 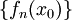 מתכנסת, אז נאמר כי סדרת הפונקציות "מתכנסת נקודתית" ונסמן
מתכנסת, אז נאמר כי סדרת הפונקציות "מתכנסת נקודתית" ונסמן 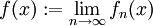 .
.
דוגמה 1
קבעו התכנסות של 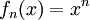 ב-
ב-![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) .
.
פתרון
נחלק לשני מקרים:
- אם
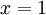 אז
אז 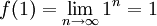 .
. - אם
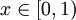 אז
אז 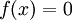 .
.
דוגמה 2
בדקו התכנסות של 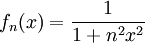 ב-
ב-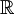 .
.
פתרון
נחלק למקרים:
הגדרה: תהינה 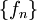 סדרת פונקציות בקטע I. נאמר כי
סדרת פונקציות בקטע I. נאמר כי  מתכנסת במ"ש אם לכל
מתכנסת במ"ש אם לכל  קיים
קיים 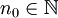 כך שלכל
כך שלכל 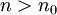 ולכל
ולכל 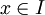 מתקיים
מתקיים 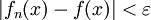 .
.
דוגמה 3
נתונה 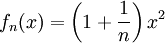 . קבע האם f מתכנסת נקודתית/במ"ש ב-
. קבע האם f מתכנסת נקודתית/במ"ש ב-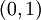 .
.
פתרון
במקרה שלנו קל לראות ש-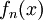 מתכנסת נקודתית ל-
מתכנסת נקודתית ל-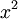 כי
כי 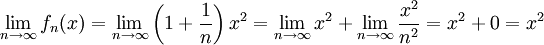
מסקנה
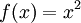
עבור התכנסות במ"ש נבדוק פי הגדרה צריך לכל  קיים
קיים 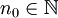 כך שלכל
כך שלכל 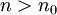 ולכל
ולכל 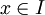 בקטע מתקיים
בקטע מתקיים 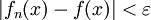 נציב עיבוד הנוסחה נכשל (שגיאת תחביר): |f_n(x)-f(x)|=\left|\left(1+\frac1n\right)x^2-x^2|=\frac{x^2}n\le\frac1n<\varepsilon
נציב עיבוד הנוסחה נכשל (שגיאת תחביר): |f_n(x)-f(x)|=\left|\left(1+\frac1n\right)x^2-x^2|=\frac{x^2}n\le\frac1n<\varepsilon
ולכן מספיק לבחורונקבל את הדרוש.
דוגמה 4
הראה כי 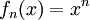 לא מתכנסת במ"ש ב-
לא מתכנסת במ"ש ב-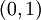 .
.
פתרון
מצאנו בדוגמה 2 ש-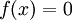 . נשים לב כי
. נשים לב כי 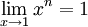 ז"א
ז"א 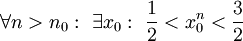 (לפי הגדרת
(לפי הגדרת