הבדלים בין גרסאות בדף "תקציר אנליזה מודרנית 1, סמסטר א תשע״ג"
מתוך Math-Wiki
(יצירת דף עם התוכן "== מידת לבג == === מידה חיצונית === בפרק זה, אלא אם צוין אחרת, <math>\{I_n\}_{n=1}^\infty</math> היא סדרת קטעים פ...") |
מ (←מידה חיצונית) |
||
| שורה 4: | שורה 4: | ||
* '''מידה חיצונית:''' תהי <math>E\subseteq\mathbb R</math>. המידה החיצונית של <math>E</math> היא <math>m^*(E):=\inf\left\{\sum_{n=1}^\infty|I_n|:\ E\subseteq\bigcup_{n=1}^\infty I_n\right\}</math>. | * '''מידה חיצונית:''' תהי <math>E\subseteq\mathbb R</math>. המידה החיצונית של <math>E</math> היא <math>m^*(E):=\inf\left\{\sum_{n=1}^\infty|I_n|:\ E\subseteq\bigcup_{n=1}^\infty I_n\right\}</math>. | ||
* <math>\forall E\subseteq\mathbb R:\ m^*(E)\in[0,\infty)</math> | * <math>\forall E\subseteq\mathbb R:\ m^*(E)\in[0,\infty)</math> | ||
| − | * <math>\forall x_0\in\mathbb | + | * <math>\forall x_0\in\mathbb R:\ m^*(\{x_0\})=m^*(\varnothing)=0</math> |
* '''מונוטוניות עולה חלשה:''' <math>\forall A\subseteq B\subseteq\mathbb R:\ m^*(A)\le m^*(B)</math>. | * '''מונוטוניות עולה חלשה:''' <math>\forall A\subseteq B\subseteq\mathbb R:\ m^*(A)\le m^*(B)</math>. | ||
* אם <math>E</math> קטע אזי <math>m^*(E)=|E|</math>. | * אם <math>E</math> קטע אזי <math>m^*(E)=|E|</math>. | ||
* אם <math>\{E_n\}_{n=1}^\infty</math> סדרת קבוצות ב־<math>\mathbb R</math> ו־<math>E=\bigcup_{n=1}^\infty E_n</math> אזי <math>m^*(E)\le\sum_{n=1}^\infty m^*(E_n)</math>. | * אם <math>\{E_n\}_{n=1}^\infty</math> סדרת קבוצות ב־<math>\mathbb R</math> ו־<math>E=\bigcup_{n=1}^\infty E_n</math> אזי <math>m^*(E)\le\sum_{n=1}^\infty m^*(E_n)</math>. | ||
* '''הזזה:''' בהנתן קבוצה <math>E</math> ו־<math>x_0\in\mathbb R</math> הקבוצה <math>x_0+E=E+x_0</math> היא הזזה שלה ומוגדרת כ־<math>\{x_0+x:\ x\in E\}</math>. | * '''הזזה:''' בהנתן קבוצה <math>E</math> ו־<math>x_0\in\mathbb R</math> הקבוצה <math>x_0+E=E+x_0</math> היא הזזה שלה ומוגדרת כ־<math>\{x_0+x:\ x\in E\}</math>. | ||
| − | * '''שמירות תחת הזזה:''' <math>\forall x_0\in\mathbb | + | * '''שמירות תחת הזזה:''' <math>\forall x_0\in\mathbb R\ \and\ E\subseteq\mathbb R:\ m^*(x_0+E)=m^*(E)</math>. |
* לא קיימת מידה <math>m</math> על <math>\mathbb R</math> המקיימת את כל התכונות הבאות: | * לא קיימת מידה <math>m</math> על <math>\mathbb R</math> המקיימת את כל התכונות הבאות: | ||
*# <math>m(E)</math> קיימת לכל <math>E\subseteq\mathbb R</math> ומקיימת <math>0\le m(E)\le\infty</math>. | *# <math>m(E)</math> קיימת לכל <math>E\subseteq\mathbb R</math> ומקיימת <math>0\le m(E)\le\infty</math>. | ||
גרסה אחרונה מ־18:50, 5 בנובמבר 2012
מידת לבג
מידה חיצונית
בפרק זה, אלא אם צוין אחרת, 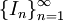 היא סדרת קטעים פתוחים. כמו כן, בהנתן קטע
היא סדרת קטעים פתוחים. כמו כן, בהנתן קטע 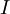 נסמן כ־
נסמן כ־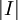 את אורכו (השווה ל־
את אורכו (השווה ל־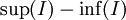 ) במקום את עוצמתו.
) במקום את עוצמתו.
- מידה חיצונית: תהי
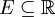 . המידה החיצונית של
. המידה החיצונית של  היא
היא 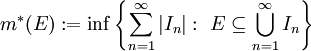 .
. -
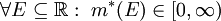
-
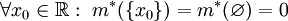
- מונוטוניות עולה חלשה:
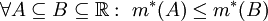 .
. - אם
 קטע אזי
קטע אזי 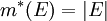 .
. - אם
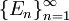 סדרת קבוצות ב־
סדרת קבוצות ב־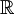 ו־
ו־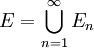 אזי
אזי 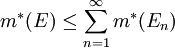 .
. - הזזה: בהנתן קבוצה
 ו־
ו־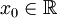 הקבוצה
הקבוצה 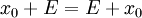 היא הזזה שלה ומוגדרת כ־
היא הזזה שלה ומוגדרת כ־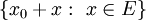 .
. - שמירות תחת הזזה:
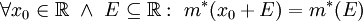 .
. - לא קיימת מידה
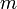 על
על 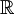 המקיימת את כל התכונות הבאות:
המקיימת את כל התכונות הבאות:
-
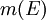 קיימת לכל
קיימת לכל 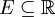 ומקיימת
ומקיימת 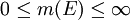 .
. - לכל קטע
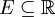 ,
, 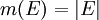 .
. -
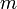 שמורה תחת הזזה.
שמורה תחת הזזה. - אם
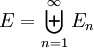 אזי
אזי 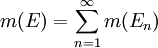 .
.
-
- קבוצה מדידה: תהי
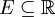 . היא תקרא "מדידה" או "מדידה לבג" אם
. היא תקרא "מדידה" או "מדידה לבג" אם 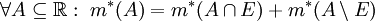 .
. - אם
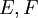 מדידות וזרות אזי
מדידות וזרות אזי 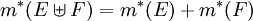 .
. -
 מדידה אם״ם
מדידה אם״ם 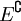 מדידה.
מדידה. -
 מדידה אם״ם
מדידה אם״ם 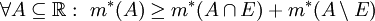 .
. - אם
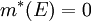 אזי
אזי  מדידה.
מדידה. - אם
 מדידה אזי לכל
מדידה אזי לכל 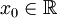 , גם
, גם 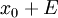 מדידה.
מדידה. - כל קטע מהצורה
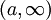 (
(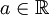 ) מדיד.
) מדיד.