הבדלים בין גרסאות בדף "תרגול 9 תשעז"

גרסה מ־19:36, 8 בינואר 2017

תרגיל

יהיו 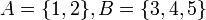$A=\{1,2\}, B=\{3,4,5\}$ . נגדיר את היחס: 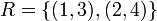$R=\{(1,3),(2,4)\}$ . בדוק האם:

א. 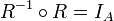$R^{-1}\circ R=I_A$

ב. 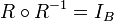$R\circ R^{-1}=I_B$

תרגיל

תהיינה 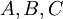$A,B,C$ קבוצות, 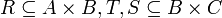$R\subseteq A\times B,T,S\subseteq B\times C$ . הוכח או הפרך:

א. 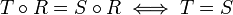$T\circ R=S\circ R\iff T=S$ .

ב. 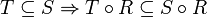$T\subseteq S\Rightarrow T\circ R\subseteq S\circ R$

פיתרון:

א. הכיוון 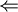$\Leftarrow$ בוודאי נכון. אבל הכיוון השני לא מתקיים. דוגמא נגדית: ניקח:

 $A=\{ 1,2\} ,R=T=\{ (1,1)\} \subseteq A\times A,S=\{ (1,1),(2,2)\} \subseteq A\times A$

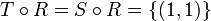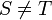ונקבל: $T\circ R=S\circ R=\{ (1,1)\}$ אבל כמובן $S\neq T$ .

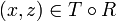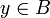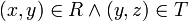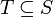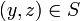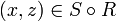ב. הוכחה: יהי $(x,z)\in T\circ R$ אזי לפי הגדרה קיים $y\in B$ כך ש- $(x,y)\in R\land (y,z)\in T$ . כעת, כיון ש- $T\subseteq S$ נובע ש- $(y,z)\in S$ , ולכן לפי הגדרת ההרכבה נקבל $(x,z)\in S\circ R$ .

תכונות של יחסים על קבוצה

הגדרה: יחס R על קבוצה A פירושו 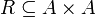$R\subseteq A\times A$

תהי קבוצה A ויחס R עליה אזי

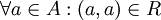R נקרא רפלקסיבי אם כל איבר מקיים את היחס עם עצמו ( מתקיים $\forall a\in A:(a,a)\in R$ )
R נקרא סימטרי אם aRb גורר שגם bRa (מתקיים $\forall a,b\in A:[(a,b)\in R \rightarrow (b,a)\in R]$ )
R נקרא טרנזיטיבי אם יחס בין ראשון לשני, ויחס בין השני לשלישי גורר יחס בין הראשון לשלישי (מתקיים $\forall a,b,c\in A:[((a,b)\in R) \and ((b,c)\in R) \rightarrow ((a,c)\in R)]$ )
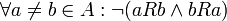R נקרא אנטי סימטרי (חלש) אם aRb וגם bRa גורר כי a=b (מתקיים $\forall a,b\in A:[(a,b)\in R \and (b,a)\in R \rightarrow a=b]$ ובאופן שקול: $\forall a\neq b\in A: \lnot (aRb\land bRa)$ )

דוגמאות:

יחס 'שיוויון' הינו רפלקסיבי, סימטרי וטרנזיטיבי
יחס 'קטן שווה' הינו רפלקסיבי, טרנזיטיבי ואנטי סימטרי
יחס 'קטן ממש' הינו טרנזיטיבי ואנטי-סימטרי
יחס 'שיוויון מודולו n' הינו רפלקסיבי, סימטרי וטרנזיטיבי
יחס 'הכלה' הינו רפלקסיבי, טרנזיטיבי ואנטי-סימטרי
יחס 'a מחלק את b' הינו רפלקסיבי וטרנזיטיבי
יחס 'אדם x שמע על אדם y' הינו רפלקסיבי

הערה: יחס יכול להיות גם סימטרי וגם אנטי סימטרי. וכמו כן הוא יכול להיות לא זה ולא זה! לדוגמא: 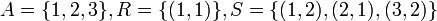$A=\{ 1,2,3\} , R=\{ (1,1)\} , S=\{ (1,2),(2,1),(3,2)\}$ ואז R גם וגם, S לא ולא.

@@ שורה 5: / שורה 5: @@
 ב. <math>R\circ R^{-1}=I_B</math>
+===תרגיל===
+תהיינה <math>A,B,C</math> קבוצות, <math>R\subseteq A\times B,T,S\subseteq B\times C</math>. הוכח או הפרך:
+א. <math>T\circ R=S\circ R\iff T=S</math>.
+ב. <math>T\subseteq S\Rightarrow T\circ R\subseteq S\circ R</math>
+'''פיתרון:'''
+א. הכיוון <math>\Leftarrow</math> בוודאי נכון. אבל הכיוון השני לא מתקיים. דוגמא נגדית: ניקח:
+ <math>A=\{ 1,2\} ,R=T=\{ (1,1)\} \subseteq A\times A,S=\{ (1,1),(2,2)\} \subseteq A\times A</math>
+ונקבל: <math>T\circ R=S\circ R=\{ (1,1)\}</math> אבל כמובן <math>S\neq T</math>.
+ב. הוכחה: יהי <math>(x,z)\in T\circ R</math> אזי לפי הגדרה קיים <math>y\in B</math> כך ש- <math>(x,y)\in R\land (y,z)\in T</math>. כעת, כיון ש-<math>T\subseteq S</math> נובע ש- <math>(y,z)\in S</math>, ולכן לפי הגדרת ההרכבה נקבל <math>(x,z)\in S\circ R</math>.
 ==תכונות של יחסים על קבוצה==

הבדלים בין גרסאות בדף "תרגול 9 תשעז"

גרסה מ־19:36, 8 בינואר 2017

תרגיל

תרגיל

תכונות של יחסים על קבוצה

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים