הבדלים בין גרסאות בדף "תרגול 9 תשעז"

גרסה מ־10:36, 10 בינואר 2017

תרגיל

יהיו 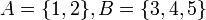$A=\{1,2\}, B=\{3,4,5\}$ . נגדיר את היחס: 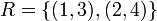$R=\{(1,3),(2,4)\}$ . בדוק האם:

א. 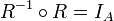$R^{-1}\circ R=I_A$

ב. 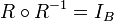$R\circ R^{-1}=I_B$

תכונות של יחסים על קבוצה

הגדרה: יחס R על קבוצה A פירושו 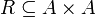$R\subseteq A\times A$

תהי קבוצה A ויחס R עליה אזי

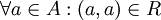R נקרא רפלקסיבי אם כל איבר מקיים את היחס עם עצמו ( מתקיים $\forall a\in A:(a,a)\in R$ )
R נקרא סימטרי אם aRb גורר שגם bRa (מתקיים $\forall a,b\in A:[(a,b)\in R \rightarrow (b,a)\in R]$ )
R נקרא טרנזיטיבי אם יחס בין ראשון לשני, ויחס בין השני לשלישי גורר יחס בין הראשון לשלישי (מתקיים $\forall a,b,c\in A:[((a,b)\in R) \and ((b,c)\in R) \rightarrow ((a,c)\in R)]$ )
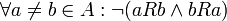R נקרא אנטי סימטרי (חלש) אם aRb וגם bRa גורר כי a=b (מתקיים $\forall a,b\in A:[(a,b)\in R \and (b,a)\in R \rightarrow a=b]$ ובאופן שקול: $\forall a\neq b\in A: \lnot (aRb\land bRa)$ )

דוגמאות:

יחס 'שיוויון' הינו רפלקסיבי, סימטרי וטרנזיטיבי
יחס 'קטן שווה' הינו רפלקסיבי, טרנזיטיבי ואנטי סימטרי
יחס 'קטן ממש' הינו טרנזיטיבי ואנטי-סימטרי
יחס 'שיוויון מודולו n' הינו רפלקסיבי, סימטרי וטרנזיטיבי
יחס 'הכלה' הינו רפלקסיבי, טרנזיטיבי ואנטי-סימטרי
יחס 'a מחלק את b' הינו רפלקסיבי וטרנזיטיבי
יחס 'אדם x שמע על אדם y' הינו רפלקסיבי

הערה: יחס יכול להיות גם סימטרי וגם אנטי סימטרי. וכמו כן הוא יכול להיות לא זה ולא זה! לדוגמא: 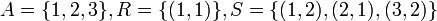$A=\{ 1,2,3\} , R=\{ (1,1)\} , S=\{ (1,2),(2,1),(3,2)\}$ ואז R גם וגם, S לא ולא.

יחסי סדר

הגדרה: יחס R על A נקרא יחס סדר חלקי אם R רפלקסיבי, טרנזיטיבי ואנטי-סימטרי

דוגמאות ליחסי סדר חלקי:

היחס 'קטן-שווה' על המספרים
היחס 'מוכל-שווה' על הקבוצות
היחס 'מחלק את ' על הטבעיים

הגדרה. דיאגרמת הסה Hesse הינה דיאגרמה של יחס סדר חלקי על קבוצה. כל איבר המקושר לאיבר מתחתיו 'גדול' ממנו ביחס. נצייר את דיאגרמת הסה ליחס הכלה על קבוצת החזקה של הקבוצה 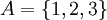$A=\{1,2,3\}$ .

הגדרות. יהיו A קבוצה וR יחס סדר חלקי על הקבוצה:

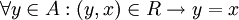איבר $x\in A$ נקרא מינמלי ביחס לR אם $\forall y\in A:(y,x)\in R \rightarrow y=x$ . כלומר, אין איבר 'קטן' מx. לא חייב להתקיים ש-x ביחס כלשהו עם איבר כלשהו.
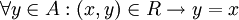איבר $x\in A$ נקרא מקסימלי ביחס לR אם $\forall y\in A:(x,y)\in R \rightarrow y=x$ . כלומר, אין איבר 'גדול' מx. לא חייב להתקיים ש-x ביחס כלשהו עם איבר כלשהו.
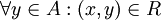איבר $x\in A$ נקרא קטן ביותר ביחס לR אם $\forall y\in A:(x,y)\in R$ . כלומר, x 'קטן' מכל האיברים. x חייב להיות ביחס עם כל האיברים בקבוצה. (דוגמא: הקבוצה הריקה תחת יחס הכלה)
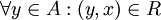איבר $x\in A$ נקרא גדול ביותר ביחס לR אם $\forall y\in A:(y,x)\in R$ . כלומר, x 'גדול' מכל האיברים. x חייב להיות ביחס עם כל האיברים בקבוצה. (דוגמא: הקבוצה B תחת יחס ההכלה על קבוצת החזקה של B)

הערה: קל להוכיח מתוך תכונת האנטי-סימטריות שאם קיים איבר קטן ביותר הוא יחיד (למרות שהוא לא חייב להיות קיים), ונכון הדבר לגבי איבר גדול ביותר.

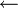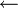הערה: קטן ביותר $\leftarrow$ מינימלי, וכן גדול ביותר $\leftarrow$ מקסימלי, ולא להיפך!

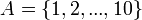צייר את דיאגרמת הסה של היחס "מחלק את" על הקבוצה $A=\{1,2,...,10\}$ מהם האיברים המינימלים והמקסימלים? האם קיים איבר קטן ביותר ואיבר גדול ביותר? צייר את היחס ההפוך של "מחלק את", זהו היחס "מתחלק ב". מהם האיברים המינימלים והמקסימלים? האם קיים איבר קטן ביותר ואיבר גדול ביותר?

@@ שורה 47: / שורה 47: @@
 הערה: קטן ביותר <math>\leftarrow</math> מינימלי, וכן גדול ביותר <math>\leftarrow</math> מקסימלי, ולא להיפך!
+צייר את דיאגרמת הסה של היחס "מחלק את" על הקבוצה <math>A=\{1,2,...,10\}</math> מהם האיברים המינימלים והמקסימלים? האם קיים איבר קטן ביותר ואיבר גדול ביותר?
+צייר את היחס ההפוך של "מחלק את", זהו היחס "מתחלק ב". מהם האיברים המינימלים והמקסימלים? האם קיים איבר קטן ביותר ואיבר גדול ביותר?

הבדלים בין גרסאות בדף "תרגול 9 תשעז"

גרסה מ־10:36, 10 בינואר 2017

תרגיל

תכונות של יחסים על קבוצה

יחסי סדר

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים