הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/טורים/מבחנים לחיוביים/דוגמאות/3"
מתוך Math-Wiki
| שורה 3: | שורה 3: | ||
*<math>\sum\frac{1}{\sqrt[n]{(n!)^2}}</math> | *<math>\sum\frac{1}{\sqrt[n]{(n!)^2}}</math> | ||
| + | '''פתרון''' | ||
| + | |||
| + | נשים לב כי <math>\lim\frac{n}{\sqrt[n]{n!}}=e</math> | ||
| + | |||
| + | ולכן <math>\lim\frac{n^2}{\sqrt[n]{n!}^2}=e^2</math> | ||
| + | |||
| + | |||
| + | ולכן הטור חבר של <math>\sum\frac{1}{n^2}</math> ולכן מתכנס. | ||
| + | |||
| + | |||
| + | |||
| + | '''פתרון ישן''' | ||
נשים לב כי לפחות '''שני שלישים''' מאיברי המכפלה <math>1\cdot 2\cdot 3 \cdots n</math> גדולים מהמספר <math>\frac{n}{3}</math>. | נשים לב כי לפחות '''שני שלישים''' מאיברי המכפלה <math>1\cdot 2\cdot 3 \cdots n</math> גדולים מהמספר <math>\frac{n}{3}</math>. | ||
גרסה מ־09:09, 4 באפריל 2012
פתרון
נשים לב כי ![\lim\frac{n}{\sqrt[n]{n!}}=e](/images/math/6/d/6/6d63df925a20e70d8da531f1d592026f.png)
ולכן ![\lim\frac{n^2}{\sqrt[n]{n!}^2}=e^2](/images/math/f/c/9/fc9b1ebb55ebe711db695fbc6040cde1.png)
ולכן הטור חבר של 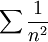 ולכן מתכנס.
ולכן מתכנס.
פתרון ישן
נשים לב כי לפחות שני שלישים מאיברי המכפלה 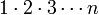 גדולים מהמספר
גדולים מהמספר 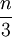 .
.
נקטין את כל האיברים במכפלה שגדולים מ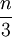 , ומכיוון שיש לפחות
, ומכיוון שיש לפחות 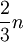 כאלה נקבל ש
כאלה נקבל ש
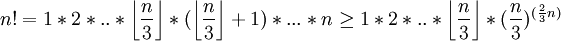
(נניח 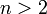 , קל לבדוק את
, קל לבדוק את 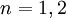 )
)
נעלה בריבוע ונקבל ש-
ולכן
אבל קל לראות כי הטורים הבאים חברים (לפי מבחן ההשוואה הגבולי)
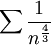 (ידוע כי טור זה מתכנס)
(ידוע כי טור זה מתכנס)
וביחד הטור מתכנס לפי מבחן ההשוואה הראשון.
![\sum\frac{1}{\sqrt[n]{(n!)^2}}](/images/math/c/5/a/c5a9f646cf481582f8df8e7006b6d15e.png)
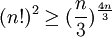
![\frac{1}{\sqrt[n]{(n!)^2}}\leq \frac{1}{\sqrt[n]{(\frac{n}{3})^{\frac{4n}{3}}}}](/images/math/1/4/5/145404f3fb2126dc453532e97e8e7e50.png)
![\sum\frac{1}{\sqrt[n]{(\frac{n}{3})^{\frac{4n}{3}}}}](/images/math/e/4/f/e4fcbf096233b48a0fef742aa27ed5e0.png)