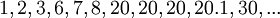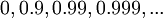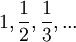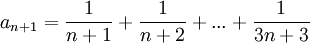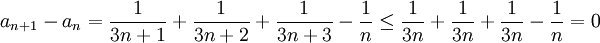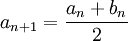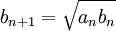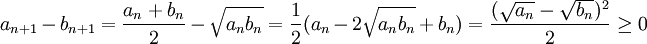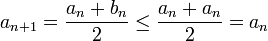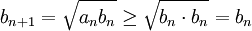הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/סדרות/מונוטוניות"
(←סדרות מונוטוניות) |
(←סדרות מונוטוניות) |
||
| שורה 52: | שורה 52: | ||
| − | '''פתרון.''' אנו נוכיח כי שתי הסדרות מונוטוניות וחסומות. ראשית, נוכיח כי איברי הסדרה <math>a_n</math> גדולים בהתאמה מאיברה הסדרה <math>b_n</math>. נשים לב כי לפי הגדרת הסדרות והאיברים הראשונים, כל איברי הסדרות הינם '''אי שליליים'''. | + | '''פתרון.''' אנו נוכיח כי שתי הסדרות מונוטוניות וחסומות. ראשית, נוכיח כי איברי הסדרה <math>a_n</math> גדולים בהתאמה מאיברה הסדרה <math>b_n</math> (פרט אולי לאיבר הראשון שיכול להבחר באופן חופשי). נשים לב כי לפי הגדרת הסדרות והאיברים הראשונים, כל איברי הסדרות הינם '''אי שליליים'''. |
::<math>a_{n+1}-b_{n+1}=\frac{a_n+b_n}{2}-\sqrt{a_nb_n}=\frac{1}{2}(a_n-2\sqrt{a_nb_n}+b_n)=\frac{(\sqrt{a_n}-\sqrt{b_n})^2}{2}\geq 0</math> | ::<math>a_{n+1}-b_{n+1}=\frac{a_n+b_n}{2}-\sqrt{a_nb_n}=\frac{1}{2}(a_n-2\sqrt{a_nb_n}+b_n)=\frac{(\sqrt{a_n}-\sqrt{b_n})^2}{2}\geq 0</math> | ||
| + | |||
| + | אם כך, מתקיים כי | ||
| + | |||
| + | ::<math>a_{n+1}=\frac{a_n+b_n}{2}\leq\frac{a_n+a_n}{2}=a_n</math> | ||
| + | |||
| + | ולכן <math>a_n</math> מונוטונית יורדת. כמו כן | ||
| + | |||
| + | ::<math>b_{n+1}=\sqrt{a_nb_n}\geq\sqrt{b_n\cdot b_n}=b_n</math> | ||
| + | |||
| + | ולכן <math>b_n</math> מונוטונית עולה. | ||
| + | |||
| + | |||
| + | נותר להראות כי הסדרות חסומות. נשים לב כי מתקיים: | ||
| + | |||
| + | ::<math>b_2\leq b_n\leq a_n \leq a_2</math> ולכן שתי הסדרות מונוטוניות וחסומות ולכן מתכנסות. | ||
גרסה מ־07:42, 3 בנובמבר 2011
סדרות מונוטוניות
הגדרה. סדרה נקראת מונוטונית עולה (יורדת) אם כל איבר בה גדול שווה לקודמו (קטן שווה לקודמו)
דוגמאות.
משפט. סדרה מונוטונית וגם חסומה מתכנסת. סדרה מונוטונית שאינה חסומה, מתכנסת במובן הרחב.
תרגיל.
הוכח שהסדרה הבאה מתכנסת 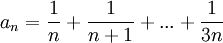
פתרון.
נוכיח כי הסדרה מונוטונית וחסומה, ואז מתכנסת לפי המשפט. נוכיח כי לכל n מתקיים 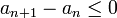 ולכן הסדרה מונוטונית יורדת.
ולכן הסדרה מונוטונית יורדת.
לכן הסדרה מונוטונית יורדת, יש לחסום אותה מלמטה על מנת שתתכנס. אבל קל לראות שכל איברי הסדרה חיוביים ולכן חסומים מלמטה על ידי אפס, ולכן הסדרה מתכנסת.
תרגיל.
יהיו 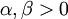 ונגדיר
ונגדיר 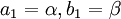 . כעת, נגדיר סדרות באמצעות נוסחאת הנסיגה (כלומר כל איבר בסדרה יוגדר באמצעות קודמיו):
. כעת, נגדיר סדרות באמצעות נוסחאת הנסיגה (כלומר כל איבר בסדרה יוגדר באמצעות קודמיו):
הוכיח כי שתי הסדרות מתכנסות.
פתרון. אנו נוכיח כי שתי הסדרות מונוטוניות וחסומות. ראשית, נוכיח כי איברי הסדרה  גדולים בהתאמה מאיברה הסדרה
גדולים בהתאמה מאיברה הסדרה  (פרט אולי לאיבר הראשון שיכול להבחר באופן חופשי). נשים לב כי לפי הגדרת הסדרות והאיברים הראשונים, כל איברי הסדרות הינם אי שליליים.
(פרט אולי לאיבר הראשון שיכול להבחר באופן חופשי). נשים לב כי לפי הגדרת הסדרות והאיברים הראשונים, כל איברי הסדרות הינם אי שליליים.
אם כך, מתקיים כי
ולכן  מונוטונית יורדת. כמו כן
מונוטונית יורדת. כמו כן
ולכן  מונוטונית עולה.
מונוטונית עולה.
נותר להראות כי הסדרות חסומות. נשים לב כי מתקיים:
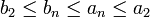 ולכן שתי הסדרות מונוטוניות וחסומות ולכן מתכנסות.
ולכן שתי הסדרות מונוטוניות וחסומות ולכן מתכנסות.