88-132 אינפי 1 סמסטר א' תשעז - תיכוניסטים
סגל הקורס:
מרצים: פרופ' בועז צבאן ופרופ' מיכאל שיין.
מתרגלים: עדי בן צבי, תמר בר און וניר שורץ.
תוכן עניינים
תשובות לערעורים נפוצים
כיון שתלמידים רבים שואלים את אותם שאלות, ועונים להם את אותם תשובות, נכתוב כאן כמה תשובות נפוצות שיחסכו לרבים מכם את הצורך לערער.
טעויות נפוצות בשאלה 5
להלן כמה טעויות נפוצות בשאלה 5. לפני שקוראים אותן, קראו את ההוכחה שבתקציר ההרצאות כדי לראות דוגמא להוכחה שנמעת מכל הבעיות האלה.
5.1 ניסוח לא נכון של ההנחה שהפונקציה אינה רציפה במידה שווה. למשל, לומר שיש שתי סדרות שהפרשן שואף לאפס אך הפרש הפונקציה עליהן (בערך מוחלט) גדול מאיזשהו מספר חיובי אפסילון. זה לא מה שאומרת ההגדרה. צריך להוכיח שאפשר להגיע למצב כזה.
5.2 הפעלת בולצנו-ויירשטרס על שתי הסדרות תפיק מהן שתי תת-סדרות מתכנסות, אבל האינדקסים של תת-הסדרות עלולים להיות שונים (כי על כל סידרה מפעילים את המשפט באופן בלתי תלוי בסדרה השניה).
5.3 כאשר האינדקסים של תת-הסדרות שנבחרו שונים, הפרש הסדרות איננו תת-סידרה של סידרת ההפרשים, ולכן לא ניתן להמשיך את הטיעון.
5.4 לומר שאם תת-סידרה מסויימת שואפת לאפס, אז הסידרה כולה שואפת לאפס.
לקראת המבחן
מאחר שהשנה לא הספקנו לדבר על נגזרות, השאלות הבאות מהמבחנים אינן בחומר:
מועד א' 2016: שאלה 5.
מועד ב' 2016: שאלה 2ב.
מועד א' 2015: שאלה 5.
מועד ב' 2015: שאלה 1 ושאלה 5ב.
מועד א' 2013: שאלות 2,6א וכן סעיפים ב',ג' בשאלה 4.
מועד ב' 2013: שאלות 2א,5,6.
מועד א' 2012: שאלות 2א,5,6.
מועד מיוחד 2012: שאלות 2ב,4 וכן שאלות 5ב,6.
מועד א' 2011: שאלות 2,6.
מועד א' 2010: שאלות 6ב,7,8.
מועד ב' 2010: שאלות 7,8.
מועד א' 2009 (זלצמן): שאלות 3א,6,8. שאלה 7: א' לא בחומר, ב' לא קשה. ג' דורש קצת מחשבה אך כן בחומר.
מועד א' 2008:שאלות 3א,6.
מועד ב' 2008: שאלה 6.
מועד א' 2007 (מירב): שאלות 2,5,6. תנאי ליפשיץ זו ההגדרה שמופיעה לכם מעל תרגיל 13.2 כבתור 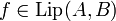 .
.
מועד ב' 2007 (מירב): שאלות 2,5,6.
מועד א' 2007 (זלצמן): שאלות 6,7,8.
מועד ב' 2007 (זלצמן): שאלות 3א,6,7,8.
מועד א' 2005: שאלות 1,5,8. כזכור נקודת הצטברות של קבוצה היא גבול של סידרת איברים מתוכה.
מועד ב' 2003: שאלות 3,9,11,14.
שאלות ותשובות למבחן
א. מהי רמת העומק שאנחנו צריכים לשאוף אליה בנוגע למשפט היינה בורל? הרי חוץ מהוכחתו לא השתמשנו בו במהלך הקורס.
הבנת ההוכחה תתן מספיק עומק לכל צורך מעשי שקשור לנושא היינה-בורל.
ב. מבנה המבחן נשאר כמו בשנים קודמות? שעתיים וחצי בחינה, 5 שאלות, מתוכן נפתור 4?
הנה עמוד המבחן הראשון. הוא עונה על השאלה. קראו אותו בעיון, ותחסכו לעצמכם זמן במבחן.
ג. האם יכולים להופיע סעיפים של ציטוטי משפטים והגדרות מושגים?
כן. אך על פי רוב, איני דורש לצטט משפט רק לפי שמו, בלי לומר על מה הוא מדבר.
ד. איך אפשר להרגע לקראת מחר? :) כל הקבוצה לחוצה מאוד, וכולם במתח לקראת מה שהולך לבוא עלינו.
המבחן השנה אמור להיות קל יחסית למי שהבין את הקורס. השתדלנו לא לתת שאלות עם טריקים הזויים (מה שלפעמים אוהבים לעשות באינפי, אבל אני לא). בואו למבחן ברצינות, אבל גם במטרה ליהנות. חשבו שאתם מקבלים פאזל מעניין להרכיב. אחרי שתכינו את עצמכם היטב, יישאר רק להנות. אולי גם כדאי להתחיל עם השאלות שנראות לכם הכי קלות, או עם שאלת ההוכחה של משפט אם יש כזו (כיון שאם יודעים את ההוכחה, זו שאלת מתנה שאפשר לסמן עליה וי ולהמשיך הלאה). זכרו ששום דבר לא יקום או ייפול על קורס בודד. היו רציניים, אך אין סיבה להיות לחוצים.
בועז
לבקשת הקהל הנה פיתרון מקוצר מאוד של המועד.
מטלות קריאה עצמית
מטלה שלישית. לקרוא את הפרק על מכפלות טורים בתקציר הקורס. להוכיח לעצמכם את הטענות שם, בעזרת הרמזים לפי הצורך. בהצלחה!
מטלה שניה. לקרוא את הפרק על מבחן השורש ומבחן המנה בתקציר הקורס. הפרק מציג גירסה משודרגת של המשפטים שלמדנו. להשלים לעצמכם את ההוכחות. בכל שאלה שיש לכם על החומר, ניתן לפנות למרצה הקורס בזמני הקבלה שלו (אצל פרופ' צבאן: לאחר כל הרצאה). אם נראה לכם שאיתרתם שם שגיאה, או שיש שימוש במשהו שטרם נלמד, נא להודיע בהקדם לפרופ' צבאן, במייל. בהצלחה!
מטלה ראשונה. לקרוא את החומר על חזקות של מספרים ממשיים. להשלים לעצמכם את ההוכחות, ולהבין כיצד חשבון גבולות תקף גם לחזקות של מספרים ממשיים. החומר נמצא בפרק 8 של תקציר הקורס תקציר הקורס. בכל שאלה שיש לכם על החומר, ניתן לפנות למרצה הקורס בזמני הקבלה שלו (אצל פרופ' צבאן: לאחר כל הרצאה). אם נראה לכם שאיתרתם שם שגיאה, או שיש שימוש במשהו שטרם נלמד, נא להודיע בהקדם לפרופ' צבאן, במייל. בהצלחה!
קישורים שימושיים
הוכחת נוסחת הסינוסים: הוכחה פשוטה של הנוסחה שסיפרו לכם בבית הספר, אך לא העזו להוכיח לכם אותה. (בפנים תראו מדוע.)
תקציר הקורס: ראשי הפרקים של ההרצאות, מפורט מאד וכולל את רעיונות ההוכחה המרכזיים ("טריקים") בכל מקום שאיננו מיידי. מתעדכן כל הזמן, לפי הדינמיקה בהרצאה. מומלץ לקרוא את החלק השייך להרצאה האחרונה לפני כל הרצאה.
מידע כללי
הציון בקורס יתחלק בצורה הבאה: 80% ציון מבחן, 10% ציון בוחן, 5% ציון במערכת התרגילים XI, ו 5% ציון בתרגילים להגשה ידנית.
שעות קבלה: לקבוצה של עדי, תמר וניר: אפשר לתאם שעות קבלה במיילים: nir.schwartz1@biu.ac.il, tamarnachshoni@gmail.com, adi2lugassy@gmail.com.
הודעות
- לסטודנטים מהקבוצה של ניר: לבקשתכם אני מצרף הוכחה מסודרת של הטענה בדבר תתי סדרות עם אינדקסים המכסים את הטבעיים. עוד אני מצרף לטובת הכלל באופן מסודר את השאלה האחרונה בה דנו בתרגול.
- פקטור לבוחן: למצער, חלק מהתלמידים לא הבינו שבקורס מתקדם הבוחן עשוי להיות משמעותי ואף קשה. בנוסף לכך היו טענות לאי הבנות, חוסר זמן, וכדומה. כיון שכך, הוחלט לתת לכלל הנבחנים פקטור מאד משמעותי ("פקטור שורש": שורש של הציון כפול 10, כלומר הממוצע הגאומטרי של ציון הבוחן והציון המקסימלי 100). לאחר דיון מעמיק וארוך, צוות הקורס החליט להשאר עם הכלל שהוכרז בתחילת הקורס, שציון הבוחן אינו מגן. ההחלטה הינה סופית. נא השתדלו לנצל את חוסר ההצלחה המספקת בבוחן כדי לדרבן את עצמכם ולמצוא דרכים להשקיע ולהתמקד בקורס, לנטרל הסחות דעת, ולהצליח ב"ה במבחן. נציין שבמבחן מעולם לא ניתן, ולא צפוי להנתן, פקטור כה גבוה. על פי רוב, במבחן לא ניתן פקטור כלל. אז טוב שהבוחן, שחלקו בציון קטן, יכול לשמש תמרור אזהרה ועידוד לשפר עוד לפני המבחן. בהצלחה רבה! מצוות הקורס
- להלן הקובץ עם ציוניכם מהתרגילים הידניים. בדקו שלא נפלו עוד טעויות. אם אתם האלמונים שהגישו את תרגיל 8 ללא שם אנא ידעו את המתרגלת שלכם בכדי שתקבלו ניקוד על עבודתכם. עודכן.--ניר (שיחה) 14:06, 7 במרץ 2017 (UTC)
- ציוני התרגילים בXI - כזכור המדיניות היא תשעת הציונים הטובים מבין השלושה עשר.
- שיעור חזרה עם ניר יתקיים ביום ד' ה-22.2 בשעה 18:00 בחדר המחלקה. השלמה של התרגילים שלא עשינו אתמול. --ניר (שיחה) 06:37, 23 בפברואר 2017 (UTC)
- שיעור חזרה עם תמר יתקיים ביום ב' ה-20.2 בשעה 16:00 בכיתה 102 בבניין 604.
- הציונים הסופיים שלכם בתרגול - תשימו לב שמי שהזנו לו בבוחן 200 סימן הוא שהוא לא מופיע ברישומים כמי שביצע את הבוחן ולכן ציונו יהיה 0 אא"כ ישלח מייל לניר בשבוע הקרוב עם צילום העמוד בבוחן שלו שעליו מופיע הציון.
הבוחן
- הבוחן יערך ביום ב' ה-26.12.16 בשעה 10:00 ומשכו 90 דקות ללא הארכת זמן.
- החומר הכלול בבוחן הוא כל דבר שראיתם בהרצאות ובתרגולים עד חנוכה. על הרצאות שלא תורגלו, לא יישאלו שאלות מסוג "תרגיל" אלא אולי רק הוכחה. השאלות דורשות בקיאות בחומר ולפיכך אנו מציעים לעבור על ההרצאות (ראו מטה), התרגולים ותרגילי הבית שניתנו במערכות השונות.
- אחת השאלות תהיה לקוחה מההרצאה אולם מי שמבין את הוכחות ההרצאה סביר להניח כי יוכל לפתח את ההוכחה בכוחותיו (נפקא מינא אנו ממליצים שלא לשנן בע"פ מבלי להבין לעומק).
- ציוני הבוחן - בהינתן סטודנט פלוני שקיבל ציון
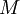 בבחינה, ציונו לאחר הפקטור הוא
בבחינה, ציונו לאחר הפקטור הוא 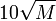 . שימו לב כי הקובץ מכיל עתה 5 ספרות אחרונות של ת.ז. והפקטורים חושבו מחדש.--ניר (שיחה) 15:40, 5 בינואר 2017 (UTC)
. שימו לב כי הקובץ מכיל עתה 5 ספרות אחרונות של ת.ז. והפקטורים חושבו מחדש.--ניר (שיחה) 15:40, 5 בינואר 2017 (UTC)
בהצלחה!
מטלות תרגול
מטלות תרגול ממוחשבות XI: בקישור. בכל שבוע יתפרסם תרגיל ביום ראשון.
הגשת המטלות: את המטלות הידניות יש להגיש בשיעור התרגול, ביום ראשון שלאחר פרסום התרגיל. את המטלות הממוחשבות יש להגיש באופן ממוחשב עד יום שני בשבוע שלאחר מתן המטלה, בחצות. לא יינתנו דחיות למועדי ההגשה. תרגילים שלא יוגשו בזמן, גם מסיבה מוצדקת, ייחשבו כתרגילים עם ציון אפס, אולם בשקלול הציון יכנסו כ-70% מהציונים הטובים ביותר.
To infinity and beyond
החומר שראית בהרצאה לא מספק אותך? תמיד חשבת שיש עולם מרהיב של אינפי מעבר לתרגילים שאנו מראים בתרגול? אם התשובה לשאלות אלו היא חיובית, פינה זו בשבילך. במהלך הסמטר יעלו לכאן חומרי העשרה ותרגילים מעניינים.
שבוע 4: סדרות מונוטוניות בתרגול של ניר ראיתם בעיה שבמקור חשב עליה סולומון גולום, מתמטיקאי שנפטר לפני כחצי שנה (מקובל לחשוב כי משחק מתמטי שהמציא היווה את ההשראה לטטריס). להלן הבעיה עם הפתרון שהצגתי בתרגול. אני מביא כאן את הבעיה בשלמותה (כולל סעיף שלא הצגתי בתרגול). הלקחים שתיקחו משאלה זו:
- יש לחשוב לפני שמבשלים בקדרה את הנוסחאתיות של המונוטוניות.
- תחומים כמו
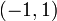 או
או ![\left[-1,1\right]](/images/math/f/f/1/ff1897f6d354c8079820a364c08e2f23.png) קשורים הדוקות לפונקציות טריגונומטריות ולא בכדי. כנובע, במקרים אלו הצבה טריגונומטרית תסייע לפתרון השאלה.
קשורים הדוקות לפונקציות טריגונומטריות ולא בכדי. כנובע, במקרים אלו הצבה טריגונומטרית תסייע לפתרון השאלה.
שבוע 6: טורים
בתרגול התחלנו לעסוק בטורים. בהקשר זה אנו מציינים תמיד את התבדרות הטור ההרמוני. מסקרן לשאול: האם יש מונח (מעניין) של "גבול מוכלל"? האם ניתן לקשר בין טורים למטריצות (אינסופיות, כמובן)? מה אפשר לומר על שיטות אלו? כל זאת ועוד במסגרת תרגיל ראשון על שיטות סכימה. חשוב להזהיר: הנושא איננו חלק מחומר הקורס כך שאין להסתמך על מונחים/משפטים מתוכו בבחינות. חשוב מכך, כשאנו כותבים 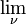 הכוונה היא לגבול במובן
הכוונה היא לגבול במובן 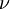 ולא במובן הרגיל. תרגיל מודרך: שיטות סכימה. כמובטח הנה פתרונות לתרגיל זה. אם יש שאלות שלחו מייל או שאלו לפני התרגול, לבחירתכם.
ולא במובן הרגיל. תרגיל מודרך: שיטות סכימה. כמובטח הנה פתרונות לתרגיל זה. אם יש שאלות שלחו מייל או שאלו לפני התרגול, לבחירתכם.
שבוע 7: טורים חיוביים טורים חיוביים הם דוגמה נהדרת לסדרות. מנגד, לרוב איננו דנים בגבולותיהם החלקיים (של סדרת הסכומים החלקיים, או בשמה "הצבאי" הסס"ח). זו הזדמנות נהדרת לעשות זאת (מיד אחרי שנתכונן לבוחן, כמובן). אני מצרף כאן פתרון בשיטת אריה במדבר.
שבוע 8: טורים המתכנסים בתנאי ובהחלט השבוע התרגיל מכיל שתי שאלות: הראשונה, לבקשתכם ובכדי שנראה שאין מעגליות בטיעונים שלנו, היא הוכחה בעזרת טכניקות של טורים חיוביים בלבד כי 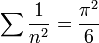 . השנייה היא הזדמנות טובה לראות כיצד טור מתכנס/מתבדר שלא בעזרת מבחני התכנסות או קריטריון Cauchy. אני חושב שהגיע הזמן לתת פיתרון לתרגיל זה. עברו ובדקו שאתם מבינים את המעברים העיקריים.
. השנייה היא הזדמנות טובה לראות כיצד טור מתכנס/מתבדר שלא בעזרת מבחני התכנסות או קריטריון Cauchy. אני חושב שהגיע הזמן לתת פיתרון לתרגיל זה. עברו ובדקו שאתם מבינים את המעברים העיקריים.
שבוע 9: סידור מחדש של איברי טור התרגיל נחלק השבוע לשני חלקים: באחד, אנו נראה קריטריון חשוב מאוד שמסייע לנו להבין סידורים מחדש של איברים של טור. כך מרוויחים הצדקה פורמלית לפעולות מסוימות במרחב המטריצות האינסופיות. לאחר מכן, אני מספק חלק נוסף לתרגיל בשיטות סכימה. חלק זה מעט מסובך ולכן תרגיל האתגר הבא שאעלה יהיה רק בעוד כשבועיים. המטרה העיקרית שם היא להוכיח באופן יצירתי כי במבחן Abel, המונוטוניות איננה דרישה הכרחית. כהערת אגב, בגרירה האחרונה במשפט 13 רצוי מאוד לצייר לעצמכם את בחירת האינדקסים. וכעת, התרגיל.
שבוע 11-12: גבולות ורציפות עוד כשהייתי סטודנט לא אהבתי את הוכחת הגבול 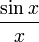 . לימים, נודע לי על הוכחה אחרת שאני אישית מחבב יותר, והיא ההדרכה בשאלה 1. בנוסף, אני שואל שאלה שתהיה רלוונטית יותר לחומר שתלמדו ביום א' הקרוב: למה אי אפשר להוכיח משפטים על פונקציות רציפות בעזרת חלוקה סופית לתתי-קטעים עליהם הן מונוטוניות? לעבודה ולמלאכה
. לימים, נודע לי על הוכחה אחרת שאני אישית מחבב יותר, והיא ההדרכה בשאלה 1. בנוסף, אני שואל שאלה שתהיה רלוונטית יותר לחומר שתלמדו ביום א' הקרוב: למה אי אפשר להוכיח משפטים על פונקציות רציפות בעזרת חלוקה סופית לתתי-קטעים עליהם הן מונוטוניות? לעבודה ולמלאכה