הבדלים בין גרסאות בדף "89-214 סמסטר א' תשעה"
(←הודעות כלליות) |
חיים רוזנר (שיחה | תרומות) |
||
| שורה 1: | שורה 1: | ||
| − | + | =הודעות כלליות= | |
| − | + | ברוכים הבאים לקורס מבנים אלגברים! | |
| − | + | '''לקבוצה של שירה: יתכן והתרגול של 07/01 יתבטל. נא להתעדכן!''' | |
| − | + | = השלמה לשיעור תרגיל בקבוצה 05 מיום כ"ח טבת (19 ינו') = | |
| − | + | '''תרגיל'''. תהי <math>G</math> חבורה מסדר <math>p^2</math> (<math>p</math> ראשוני). הראו כי <math>|Z(G)|\neq p</math>. | |
| − | = | + | '''פתרון'''. נניח בשלילה כי <math>|Z(G)|=p</math>. מכיוון שזו חבורה מסדר ראשוני היא ציקלית, כלומר קיים <math>a \in Z(G)</math> שיקיים <math><a>=Z(G)</math>. בנוסף, משיקולי עוצמה, קיים איבר <math>b \in G-Z(G)</math>. ננסה להראות כי <math>b</math> הזה מתחלף עם כל איברי <math>G</math>, ולכן <math>b\in Z(G)</math>, ובסתירה לבחירת <math>b</math>. |
| − | + | ראשית, נשים לב לכך שהסדר של <math>b</math> הוא <math>p</math>; אילו הסדר היה <math>p^2</math> אז <math>b</math> היה יוצר של כל <math>G</math>, ואילו הסדר היה <math>1</math> אז הוא היה איבר היחידה. הסדר של <math>a</math> גם הוא <math>p</math>, באופן ברור. | |
| − | ''' | + | כעת, נביט בקבוצה <math>H=<a,b>=\{a^i b^j | 0 \le i,j \le p-1\}</math>. נראה כי <math>H</math> היא קבוצה מעוצמה <math>p^2</math>: נניח כי קיימים <math>(i,j)\neq(i',j')</math> עבורם <math>{a^i}{b^j}={a^{i'}}{b^{j'}}</math>. על ידי בידוד איברים, נקבל <math>a^{i-i'}=b^{j'-j}</math>, והאפשרות היחידה היא ששני ביטויים אלה שווים <math>e</math>, ובסתירה להנחה <math>(i,j)\neq(i',j')</math>. אם כן, לא ספרנו כאן איבר אחד פעמיים, ומצאנו שעוצמת <math>H</math> היא <math>p^2</math>. |
| + | |||
| + | ברור ש-<math>H\subseteq G</math>, ולפי שויון עוצמות סופיות, <math>H=G</math>. לכן כל איבר ב-<math>G</math> ניתן לרשום בתור <math>a^ib^j</math>. נבדוק האם <math>b \cdot a^ib^j=a^ib^j \cdot b</math>. | ||
| + | |||
| + | ראשית, נזכיר כי <math>ab=ba</math>, כי <math>a\in Z(G)</math>. לכן <math>b\cdot a^i=b\cdot a\cdot a^{i-1}=a\cdot b\cdot a^{i-1}</math>. נחזור על הטיעון <math>i</math> פעמים, ונקבל <math>b\cdot a^i=a^i\cdot b</math>. כמו כן, ברור כי <math>b\cdot b^j=b^j\cdot b</math>. ביחד, נקבל <math>b\cdot a^ib^j=a^i\cdot b \cdot b^j = a^ib^j\cdot b</math>, כנדרש. מצאנו אפוא כי <math>b\in Z(G)</math>, ובסתירה לדרך שבה בחרנו את <math>b</math>. | ||
| + | |||
| + | '''תרגיל'''. תהי <math>G</math> חבורה מסדר <math>p^2</math> (<math>p</math> ראשוני). הראו כי היא חבורה אבלית. | ||
| + | |||
| + | '''פתרון'''. לפי התרגיל הקודם, <math>|Z(G)|\neq p</math>. לפי נוסחת המחלקות, <math>|Z(G)|\neq 1</math> (הראנו בכיתה). לפי לגרנז', <math>|Z(G)| \mid p^2</math>, וביחד נקבל <math>|Z(G)|= p^2</math>. אם כן, משויון עוצמת קבוצות סופיות, <math>Z(G)=G</math>, ו-<math>G</math> אבלית. | ||
גרסה מ־12:47, 19 בינואר 2015
הודעות כלליות
ברוכים הבאים לקורס מבנים אלגברים!
לקבוצה של שירה: יתכן והתרגול של 07/01 יתבטל. נא להתעדכן!
השלמה לשיעור תרגיל בקבוצה 05 מיום כ"ח טבת (19 ינו')
תרגיל. תהי  חבורה מסדר
חבורה מסדר 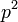 (
(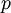 ראשוני). הראו כי
ראשוני). הראו כי 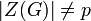 .
.
פתרון. נניח בשלילה כי 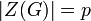 . מכיוון שזו חבורה מסדר ראשוני היא ציקלית, כלומר קיים
. מכיוון שזו חבורה מסדר ראשוני היא ציקלית, כלומר קיים 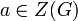 שיקיים
שיקיים 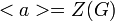 . בנוסף, משיקולי עוצמה, קיים איבר
. בנוסף, משיקולי עוצמה, קיים איבר 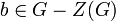 . ננסה להראות כי
. ננסה להראות כי 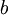 הזה מתחלף עם כל איברי
הזה מתחלף עם כל איברי  , ולכן
, ולכן 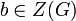 , ובסתירה לבחירת
, ובסתירה לבחירת 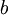 .
.
ראשית, נשים לב לכך שהסדר של 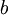 הוא
הוא 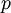 ; אילו הסדר היה
; אילו הסדר היה 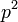 אז
אז 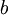 היה יוצר של כל
היה יוצר של כל  , ואילו הסדר היה
, ואילו הסדר היה 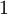 אז הוא היה איבר היחידה. הסדר של
אז הוא היה איבר היחידה. הסדר של  גם הוא
גם הוא 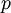 , באופן ברור.
, באופן ברור.
כעת, נביט בקבוצה 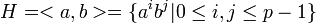 . נראה כי
. נראה כי 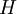 היא קבוצה מעוצמה
היא קבוצה מעוצמה 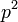 : נניח כי קיימים
: נניח כי קיימים 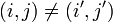 עבורם
עבורם 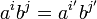 . על ידי בידוד איברים, נקבל
. על ידי בידוד איברים, נקבל 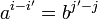 , והאפשרות היחידה היא ששני ביטויים אלה שווים
, והאפשרות היחידה היא ששני ביטויים אלה שווים 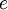 , ובסתירה להנחה
, ובסתירה להנחה 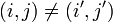 . אם כן, לא ספרנו כאן איבר אחד פעמיים, ומצאנו שעוצמת
. אם כן, לא ספרנו כאן איבר אחד פעמיים, ומצאנו שעוצמת 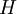 היא
היא 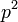 .
.
ברור ש-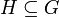 , ולפי שויון עוצמות סופיות,
, ולפי שויון עוצמות סופיות, 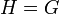 . לכן כל איבר ב-
. לכן כל איבר ב- ניתן לרשום בתור
ניתן לרשום בתור 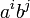 . נבדוק האם
. נבדוק האם 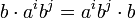 .
.
ראשית, נזכיר כי 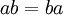 , כי
, כי 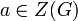 . לכן
. לכן 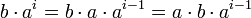 . נחזור על הטיעון
. נחזור על הטיעון 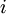 פעמים, ונקבל
פעמים, ונקבל 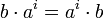 . כמו כן, ברור כי
. כמו כן, ברור כי 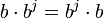 . ביחד, נקבל
. ביחד, נקבל 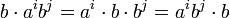 , כנדרש. מצאנו אפוא כי
, כנדרש. מצאנו אפוא כי 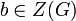 , ובסתירה לדרך שבה בחרנו את
, ובסתירה לדרך שבה בחרנו את 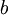 .
.
תרגיל. תהי  חבורה מסדר
חבורה מסדר 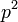 (
(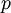 ראשוני). הראו כי היא חבורה אבלית.
ראשוני). הראו כי היא חבורה אבלית.
פתרון. לפי התרגיל הקודם, 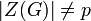 . לפי נוסחת המחלקות,
. לפי נוסחת המחלקות, 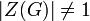 (הראנו בכיתה). לפי לגרנז',
(הראנו בכיתה). לפי לגרנז', 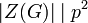 , וביחד נקבל
, וביחד נקבל 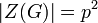 . אם כן, משויון עוצמת קבוצות סופיות,
. אם כן, משויון עוצמת קבוצות סופיות, 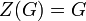 , ו-
, ו- אבלית.
אבלית.