התכנסות במידה שווה (המשך)

תזכורת: תהי [math]\displaystyle{ \{f_n\} }[/math] סדרת פונקציות בקטע I כך שלכל [math]\displaystyle{ x\in I }[/math] קיים הגבול [math]\displaystyle{ f(x)=\lim_{n\to\infty} f_n(x) }[/math] (כלומר, הפונקציה הגבולית מוגדרת בכל I). הגדרנו ש-[math]\displaystyle{ f_n\to f }[/math] במידה שווה ב-I אם לכל [math]\displaystyle{ \varepsilon\gt 0 }[/math] קיים [math]\displaystyle{ n_0\in\mathbb N }[/math] כך שאם [math]\displaystyle{ n\gt n_0 }[/math] אז [math]\displaystyle{ |f(x)-f_n(x)|\lt \varepsilon }[/math] לכל [math]\displaystyle{ x\in I }[/math].

הערה

אם [math]\displaystyle{ f_n\to f }[/math] במ"ש על I אז לכל [math]\displaystyle{ x\in I }[/math] ברור שמתקיים [math]\displaystyle{ f(x)=\lim_{n\to\infty} f_n(x) }[/math], כלומר התכנסות במ"ש גוררת התכנסות נקודתית. ההיפך אינו נכון.

משפט 1

יהיו קבוצת הפונקציות [math]\displaystyle{ \{f_n\} }[/math] והפונקציה f מוגדרות בקטע I. אז התנאים הבאים שקולים:

[math]\displaystyle{ f(x)=\lim_{n\to\infty} f_n(x) }[/math] במ"ש ב-I
[math]\displaystyle{ \lim_{n\to\infty}\sup_{x\in I}|f(x)-f_n(x)|=0 }[/math]

הוכחה

ראשית נוכיח שהתנאי הראשון גורר את השני: אם נגדיר לכל n את [math]\displaystyle{ a_n=\sup_{x\in I}|f(x)-f_n(x)| }[/math] אז יש להוכיח כי [math]\displaystyle{ \lim_{n\to\infty} a_n=0 }[/math]. אבל אם [math]\displaystyle{ \varepsilon\gt 0 }[/math] ידוע כי קיים [math]\displaystyle{ n_0\in\mathbb N }[/math] כך שלכל [math]\displaystyle{ n\gt n_0 }[/math] מתקיים [math]\displaystyle{ |f(x)-f_n(x)|\lt \frac\varepsilon2 }[/math] לכל [math]\displaystyle{ x\in I }[/math]. נובע מיד שאם [math]\displaystyle{ n\gt n_0 }[/math] אז [math]\displaystyle{ 0\le a_n=\sup_{x\in I}|f(x)-f_n(x)|\le\frac\varepsilon2\lt \varepsilon }[/math] ולכן [math]\displaystyle{ \forall n\gt n_0:\ |a_n-0|\lt \varepsilon }[/math] והוכחנו [math]\displaystyle{ a_n\to0 }[/math], כדרוש.

לצד השני יהי [math]\displaystyle{ \varepsilon\gt 0 }[/math] נתון. ידוע כי קיים [math]\displaystyle{ n_0\in\mathbb N }[/math] כך שלכל [math]\displaystyle{ n\gt n_0 }[/math] מתקיים [math]\displaystyle{ \sup_{x\in I}|f(x)-f_n(x)|\lt \varepsilon }[/math] ולכן [math]\displaystyle{ \forall n\gt n_0:\ |f(x)-f_n(x)|\lt \varepsilon }[/math] עבור [math]\displaystyle{ x\in I }[/math]. [math]\displaystyle{ \blacksquare }[/math]

דוגמה

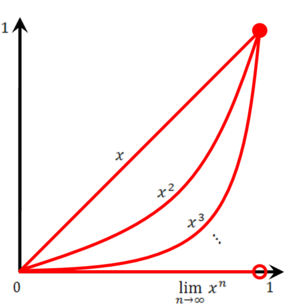
בקטע [math]\displaystyle{ [0,1) }[/math] ברור כי [math]\displaystyle{ \lim_{n\to\infty}x^n=0 }[/math].

נראה כי ההתכנסות נקודתית ולא במ"ש: [math]\displaystyle{ \forall n\in\mathbb N:\ a_n=\sup_{x\in[0,1)}|x^n-0|=1\ne0 }[/math]. [math]\displaystyle{ \blacksquare }[/math]

נעיר כי בקטע [math]\displaystyle{ [0,r] }[/math] עבור [math]\displaystyle{ r\lt 1 }[/math] דווקא יש התכנסות במ"ש: [math]\displaystyle{ \forall n\in\mathbb N:\ a_n=\sup_{x\in[0,r]}|x^n-0|=r^n }[/math] ולכן [math]\displaystyle{ \lim_{n\to\infty}a_n=\lim_{n\to\infty}r^n=0 }[/math], כדרוש. [math]\displaystyle{ \blacksquare }[/math]

משפט 2

נניח ש-[math]\displaystyle{ \lim_{n\to\infty} f_n(x)=f(x) }[/math] במ"ש ב-I. עוד נניח שעבור איזה [math]\displaystyle{ x_0\in I }[/math] כל [math]\displaystyle{ f_n }[/math] רציפה ב-[math]\displaystyle{ x_0 }[/math]. אזי גם f רציפה ב-[math]\displaystyle{ x_0 }[/math].

הוכחה

יהי [math]\displaystyle{ \varepsilon\gt 0 }[/math] נתון. [math]\displaystyle{ f_n\to f }[/math] במ"ש ב-I ולכן קיים n טבעי מסויים כך שלכל [math]\displaystyle{ x\in I }[/math] מתקיים [math]\displaystyle{ |f(x)-f_n(x)|\lt \frac\varepsilon3 }[/math]. [math]\displaystyle{ f_n }[/math] רציפה ב-[math]\displaystyle{ x_0 }[/math] ולכן קיים [math]\displaystyle{ \delta\gt 0 }[/math] כך שאם [math]\displaystyle{ |x-x_0|\lt \delta }[/math] אז [math]\displaystyle{ |f_n(x)-f_n(x_0)|\lt \frac\varepsilon3 }[/math] נובע שאם [math]\displaystyle{ |x-x_0|\lt \delta }[/math] אז [math]\displaystyle{ |f(x)-f(x_0)|\le|f(x)-f_n(x)|+|f_n(x)-f_n(x_0)|+|f_n(x_0)-f(x_0)|\lt \frac\varepsilon3+\frac\varepsilon3+\frac\varepsilon3=\varepsilon }[/math]. [math]\displaystyle{ \blacksquare }[/math]

מסקנה

בתנאים של משפט 2, אם כל [math]\displaystyle{ f_n }[/math] רציפה בקטע I כולו, אז גם f רציפה ב-I כולו.

דוגמה

בקטע [math]\displaystyle{ [0,1] }[/math] ברור כי [math]\displaystyle{ \lim_{n\to\infty}x^n=\begin{cases}0&0\le x\lt 1\\1&x=1\end{cases} }[/math]. כאן כל [math]\displaystyle{ x^n }[/math] רציפה ב-[math]\displaystyle{ [0,1] }[/math] ואילו הפונקציה הגבולית לא רציפה. זה אינו סותר את משפט 2 כי כבר ראינו שההתכנסות אינה במ"ש.

משפט 3

נניח שלכל n [math]\displaystyle{ f_n }[/math] מוגדרת ואינטגרבילית ב-[math]\displaystyle{ I=[a,b] }[/math] ונניח שקיים [math]\displaystyle{ f(x)=\lim_{n\to\infty}f_n(x) }[/math] במ"ש ב-I. אזי f אינטגרבילית ב-I ומתקיים [math]\displaystyle{ \int\limits_a^b f=\lim_{n\to\infty}\int\limits_a^b f_n }[/math].

הוכחה

לא נוכיח שבתנאים הללו f אינטגרבילית (בד"כ זה יתקיים אוטומטית אם כל ה-[math]\displaystyle{ f_n }[/math] רציפות למקוטעין), ונסתפק בהוכחה לכך ש-[math]\displaystyle{ \int\limits_a^b f=\lim_{n\to\infty}\int\limits_a^b f_n }[/math]. שקול להוכיח ש-[math]\displaystyle{ \lim_{n\to\infty}\int\limits_a^b f-\int\limits_a^b f_n=0 }[/math]. ובכן יהי [math]\displaystyle{ \varepsilon\gt 0 }[/math] נתון. כיוון ש-[math]\displaystyle{ f_n\to f }[/math] במ"ש על I [math]\displaystyle{ \exists n_0\in\mathbb N:\ \forall n\gt n_0:\ \sup_{x\in[a,b]}|f(x)-f_n(x)|\lt \frac\varepsilon{b-a} }[/math]. נובע שלכל [math]\displaystyle{ n\gt n_0 }[/math] [math]\displaystyle{ \left|\int\limits_a^b(f-f_n)\right|\le\int\limits_a^b|f-f_n|\le(b-a)\sup_{x\in I}|f(x)-f_n(x)|\lt (b-a)\frac\varepsilon{b-a}=\varepsilon }[/math]. מכאן נובע ש-[math]\displaystyle{ \lim_{n\to\infty}\left|\int\limits_a^b (f-f_n)\right|=0 }[/math]. [math]\displaystyle{ \blacksquare }[/math]

דוגמה

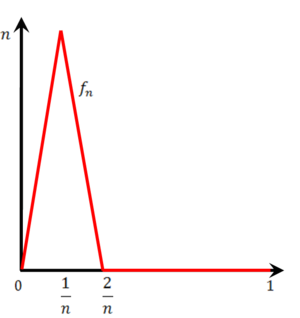
משמאל נתונה הפונקציה [math]\displaystyle{ f_n }[/math] עבור [math]\displaystyle{ n\in\mathbb N }[/math] כלשהו.

נוכיח כי [math]\displaystyle{ \forall x\in[0,1]:\ \lim_{n\to\infty}f_n(x)=0 }[/math]: עבור [math]\displaystyle{ x=0 }[/math] לכל n [math]\displaystyle{ f_n(0)=0 }[/math] ולכן [math]\displaystyle{ \lim_{n\to\infty} f_n(0)=0 }[/math]. אם [math]\displaystyle{ x\in(0,1] }[/math] אז קיים [math]\displaystyle{ n_0\in\mathbb N }[/math] כך ש-[math]\displaystyle{ \frac2{n_0}\lt x }[/math] ולכן לכל [math]\displaystyle{ n\gt n_0 }[/math] מתקיים [math]\displaystyle{ \frac2n\lt \frac2{n_0}\lt x }[/math], מה שגורר כי [math]\displaystyle{ f_n(x)=0 }[/math] לכל [math]\displaystyle{ n\in\mathbb N }[/math] ונובע ש-[math]\displaystyle{ \lim_{n\to\infty}f_n(x)=0 }[/math]. בזה הוכחנו את הטענה ש-[math]\displaystyle{ 0=\lim_{n\to\infty}f_n(x) }[/math] נקודתית ב-[math]\displaystyle{ [0,1] }[/math]. [math]\displaystyle{ \blacksquare }[/math] נעיר שההתכנסות "מאוד" לא במ"ש כי [math]\displaystyle{ \sup_{x\in[0,1]}|f_n(x)-0|=n\to\infty }[/math].

נוכיח כי [math]\displaystyle{ \lim_{n\to\infty}\int\limits_0^1 f_n\ne\int\limits_0^1 0\mathrm dx }[/math] (כאשר [math]\displaystyle{ f(x)=0 }[/math] היא הפונקציה הגבולית): לכל n

[math]\displaystyle{ \int\limits_0^1 f_n= }[/math] השטח מתחת לגרף [math]\displaystyle{ =\frac12\cdot n\cdot\frac2n=1\ne0 }[/math]

[math]\displaystyle{ \blacksquare }[/math]

השערה סבירה אבל מאוד לא נכונה: אם [math]\displaystyle{ f_n\to f }[/math] במ"ש ב-I אז [math]\displaystyle{ f_n'\to f' }[/math] ב-I. דוגמה נגדית: נגדיר [math]\displaystyle{ f_n(x)=\frac{\sin\left(n^2x\right)}n }[/math].

נוכיח ש-[math]\displaystyle{ \lim_{n\to\infty} f_n(x)=0 }[/math] במ"ש בכל [math]\displaystyle{ \mathbb R }[/math]: [math]\displaystyle{ \forall n\in\mathbb N:\ a_n=\sup_{x\in\mathbb R}\left|\frac{\sin\left(n^2x\right)}n-0\right|=\sup_{x\in\mathbb R}\frac{\left|\sin\left(n^2x\right)\right|}n=\frac1n\to0 }[/math].
נוכיח [math]\displaystyle{ f_n'\not\to0'=0 }[/math]: לכל n ולכל [math]\displaystyle{ x\in\mathbb R }[/math] מתקיים [math]\displaystyle{ f_n'(x)=n\cos\left(n^2x\right) }[/math] ועבור [math]\displaystyle{ x\in\mathbb R }[/math] כלשהו [math]\displaystyle{ \lim_{n\to\infty}f_n'(x)=\lim_{n\to\infty} n\cos\left(n^2x\right) }[/math] שאינו קיים. [math]\displaystyle{ \blacksquare }[/math]

משפט 4

תהי [math]\displaystyle{ \{f_n\} }[/math] סדרת פונקציות בעלות נגזרות רציפות [math]\displaystyle{ f_n' }[/math] בקטע I. נניח שהסדרה [math]\displaystyle{ \{f_n\} }[/math] מתכנסת בנקודה אחת (לפחות) [math]\displaystyle{ x_0\in I }[/math] והסדרה [math]\displaystyle{ \{f_n'\} }[/math] מתכנסת במ"ש ל-g ב-I. אזי [math]\displaystyle{ \lim_{n\to\infty} f_n(x) }[/math] קיים לכל [math]\displaystyle{ x\in I }[/math] ומגדיר פונקציה גבולית f שהיא גזירה ב-I. יתר על כן [math]\displaystyle{ \forall x\in I:\ f'(x)=g(x) }[/math].

הוכחה

נקח [math]\displaystyle{ x\in I }[/math] כלשהו. לכל n הפונקציה [math]\displaystyle{ f_n' }[/math] רציפה (נתון) ונוכל להפעיל את המשפט היסודי לומר [math]\displaystyle{ f_n(x)-f_n(x_0)=\int\limits_{x_0}^x f_n' }[/math]. נעביר אגף: [math]\displaystyle{ f_n(x)=f_n(x_0)+\int\limits_{x_0}^x f_n' }[/math]. כעת נתון שקיים [math]\displaystyle{ \lim_{n\to\infty} f_n(x_0) }[/math], נקרא לו [math]\displaystyle{ \alpha }[/math]. יתר על כן נתון ש-[math]\displaystyle{ \lim_{n\to\infty} f_n'(t)=g(t) }[/math] במ"ש ב-I וכל שכן [math]\displaystyle{ \lim_{n\to\infty}f_n'(t)=g(t) }[/math] במ"ש בתת הקטע בין [math]\displaystyle{ x_0 }[/math] ל-x. נסיק ממשפט 3 ש-[math]\displaystyle{ \lim_{n\to\infty}\int\limits_{x_0}^x f_n'=\int\limits_{x_0}^x g }[/math] נובע שלכל [math]\displaystyle{ x\in I }[/math] קיים [math]\displaystyle{ f(x)=\lim_{n\to\infty} f_n(x)=\lim_{n\to\infty}\left(f_n(x_0)+\int\limits_{x_0}^x f_n'\right)=\alpha+\int\limits_{x_0}^x g }[/math] והוכחנו את קיום הפונקציה הגבולית f. נותר להוכיח שהיא גזירה וש-[math]\displaystyle{ \forall x\in[a,b]:\ f'(x)=g(x) }[/math]. לפי הנתון כל [math]\displaystyle{ f_n' }[/math] רציפה ו-[math]\displaystyle{ g(t)=\lim_{n\to\infty} f_n'(t) }[/math] במ"ש על I. לכן משפט 2 נותן ש-[math]\displaystyle{ g }[/math] רציפה ב-I וכיוון שלכל [math]\displaystyle{ x\in I }[/math] מתקיים [math]\displaystyle{ f(x)=\alpha+\int\limits_{x_0}^x g }[/math] החלק הראשון של המשפט היסודי נותן [math]\displaystyle{ f'=g }[/math] לכל [math]\displaystyle{ x\in I }[/math]. [math]\displaystyle{ \blacksquare }[/math]