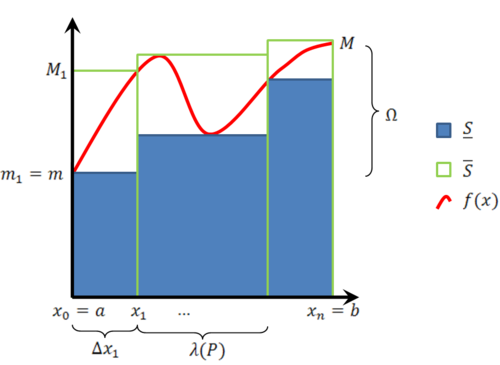
סכום דרבו
הגדרה
תהי [math]\displaystyle{ f }[/math] מוגדרת וחסומה בקטע [math]\displaystyle{ [a,b] }[/math] ותהי [math]\displaystyle{ P=\{x_0,x_1,\ldots,x_n\} }[/math] חלוקה של הקטע.
לכל [math]\displaystyle{ k }[/math] כך ש- [math]\displaystyle{ 1\le k\le n }[/math] נגדיר גם נקודות גובה מקסימלי ומינימלי בקטע (יש לשים לב שהסופרמום והאינפימום אינם בהכרח שווים למקסימום ולמינימום בקטע):
- [math]\displaystyle{ M_k:=\sup\big\{f(x):x_{k-1}\le x\le x_k\big\} }[/math]
- [math]\displaystyle{ m_k:=\inf\big\{f(x):x_{k-1}\le x\le x_k\big\} }[/math]
בהתאם לכך נגדיר:
- שטח חוסם - סכום דארבו עליון: [math]\displaystyle{ \overline S(f,P):=\sum\limits_{k=1}^n M_k\Delta x_k }[/math]
- שטח חסום - סכום דארבו תחתון: [math]\displaystyle{ \underline S(f,P):=\sum\limits_{k=1}^n m_k\Delta x_k }[/math]