משתמש:אור שחף/133 - הרצאה/31.5.11: הבדלים בין גרסאות בדף
(יצירת דף עם התוכן "{{הערה|את דוגמה 4 לא סיימנו בהרצאה הקודמת ולכן השלמנו אותה ב-31.5.11. [[משתמש:אור שחף/133 - הרצאה/29.5...") |
מאין תקציר עריכה |
||
| (3 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
{{ | {{המשך הגיע|תיאור=דוגמה 4|תאריך=29.5.11}} | ||
=טורי חזקות {{הערה|(המשך)}}= | =טורי חזקות {{הערה|(המשך)}}= | ||
| שורה 9: | שורה 9: | ||
===הוכחה=== | ===הוכחה=== | ||
נעזר בסכימה בחלקים: נסמן <math>S_N=\sum_{n=0}^N a_n</math> ולכן <math>\forall N\in\mathbb N:\ \sum_{n=0}^Na_nx^n=\sum_{n=0}^{N-1}S_n\left(x^n-x^{n+1}\right)+S_Nx^N</math> כאשר <math>-1<x<1</math>. לפי הנתון <math>S=\lim_{N\to\infty}S_N</math>, ולכן אם <math>0<x<1</math> אז <math>\lim_{N\to\infty}S_Nx^N=0</math> ועבור <math>0\le x\le 1</math> מתקיים <math>f(x)=\sum_{n=0}^\infty a_nx^n=\sum_{n=0}^\infty S_n\left(x^n-x^{n+1}\right)=(1-x)\sum_{n=0}^\infty S_nx^n</math>. כמו כן, <math>\forall x\in[0,1):\ 1=(1-x)\ | נעזר בסכימה בחלקים: נסמן <math>S_N=\sum_{n=0}^N a_n</math> ולכן <math>\forall N\in\mathbb N:\ \sum_{n=0}^Na_nx^n=\sum_{n=0}^{N-1}S_n\left(x^n-x^{n+1}\right)+S_Nx^N</math> כאשר <math>-1<x<1</math>. לפי הנתון <math>S=\lim_{N\to\infty}S_N</math>, ולכן אם <math>0<x<1</math> אז <math>\lim_{N\to\infty}S_Nx^N=0</math> ועבור <math>0\le x\le 1</math> מתקיים <math>f(x)=\sum_{n=0}^\infty a_nx^n=\sum_{n=0}^\infty S_n\left(x^n-x^{n+1}\right)=(1-x)\sum_{n=0}^\infty S_nx^n</math>. כמו כן, <math>\forall x\in[0,1):\ 1=(1-x)\sum_{n=0}^\infty x^n</math> (כי <math>\frac1{1-x}=\sum_{n=0}^\infty x^n</math>). לכן <math>S=(1-x)\sum_{n=0}^\infty Sx^n</math> ומכאן שעבור <math>x\in[0,1)</math> מתקיים <math>f(x)-S=(1-x)\sum_{n=0}^\infty(S_n-S)x^n</math>. נרצה להוכיח ש-<math>\lim_{x\to1^-}f(x)-S=0</math>: יהי <math>\varepsilon>0</math> נתון ומכיוון ש-<math>\lim_{n\to\infty}S_n=S</math> קיים <math>n_0\in\mathbb N</math> כך שלכל <math>n>n_0</math> יתקיים <math>|S_n-S|<\frac\varepsilon2</math>. נסמן <math>I_1=(1-x)\sum_{n=0}^{n_0}(S_n-S)x^n</math> וכן <math>I_2=(1-x)\sum_{n=n_0+1}^\infty(S_n-S)x^n</math>, לכן <math>f(x)-S=I_1+I_2</math>. עתה <math>|I_2|\le(1-x)\sum_{n=n_0+1}^\infty|S_n-S|x^n<\frac\varepsilon2(1-x)\sum_{n=n_0+1}^\infty x^n\le\frac\varepsilon2(1-x)\sum_{n=0}^\infty x^n=\frac\varepsilon2</math>. לגבי <math>I_1</math> נגדיר <math>M=\sum_{n=0}^{n_0}|S_n-S|</math> ולכן <math>|I_1|\le(1-x)\sum_{n=0}^{n_0}|S_n-S|</math>. עתה <math>x\to1^-</math> ולכן <math>0<1-x<\frac\varepsilon{2M}</math>, לכן <math>|I_1|\le\frac\varepsilon{2M}M=\frac\varepsilon2</math>. לסיכום הוכחנו שאם <math>1-\frac\varepsilon{2M}<x<1</math> אזי <math>|f(x)-S|<|I_1|+|I_2|<\varepsilon</math> ולכן <math>\lim_{x\to1^-}f(x)-S=0</math>. {{משל}} | ||
===מסקנה=== | ===מסקנה=== | ||
לגבי טור חזקות כללי <math>f(x)=\sum_{n=0}^\infty a_n(x-x_0)^n</math> בעל רדיוס התכנסות R: | לגבי טור חזקות כללי <math>f(x)=\sum_{n=0}^\infty a_n(x-x_0)^n</math> בעל רדיוס התכנסות R: | ||
# אם <math>\sum_{n=0}^\infty a_nR^n</math> מתכנס ל-S אזי <math>\lim_{x\to x_0+R^-}f(x)</math> קיים ושווה ל-S. | # אם <math>\sum_{n=0}^\infty a_nR^n</math> מתכנס ל-S אזי <math>\lim_{x\to x_0+R^-}f(x)</math> קיים ושווה ל-S. | ||
# אם <math>\sum_{n=0}^\infty a_n(-R)^n</math> מתכנס ל-T אזי <math>\lim_{x\to x_0-R^+}f(x)</math> קיים ושווה ל-T. | # אם <math>\sum_{n=0}^\infty a_n(-R)^n</math> מתכנס ל-T אזי <math>\lim_{x\to(x_0-R)^+}f(x)</math> קיים ושווה ל-T. | ||
====הוכחה==== | ====הוכחה==== | ||
| שורה 31: | שורה 31: | ||
===הוכחה=== | ===הוכחה=== | ||
במקרה הראשון נניח שסדרת הפונקציות יורדת מונוטונית. לכן <math>\{f_n-f\}</math> היא סדרת פונקציות יורדת מונוטונית השואפת ל-0 ב-<math>[a,b]</math>. נסמן <math>g_n=f_n-f</math> (ולכן <math>g_n</math> חיובית) ונניח בשלילה שההתכנסות <math>g_n\to0</math> אינה במ"ש בקטע. לפיכך קיים <math>\varepsilon>0</math> כל שלכל <math>n_0\in\mathbb N</math> קיימים <math>n>n_0</math> ו-<math>x\in[a,b]</math> עבורם <math>g_n(x)>\varepsilon</math>. בפרט, עבור <math>n_0=1</math> קיימים <math>n_1>n_0</math> ו-<math>x_1\in[a,b]</math> כך ש-<math>g_{n_1}(x_1)>\varepsilon</math>. עבור <math>n_0=n_1+1</math> קיימים <math>n_2>n_0</math> ו-<math>x_2\in[a,b]</math> כך ש-<math>g_{n_2}(x_2)>\varepsilon</math> וכן הלאה. בדרך זו בונים תת סדרה <math>\{g_{n_k}\}</math> של <math>\{g_n\}</math> וסדרה <math>\{x_k\}</math> ב-<math>[a,b]</math> כך ש-<math>\forall k:\ g_{n_k}(x_k)>\varepsilon</math>. <math>\{x_k\}</math> נמצאת ב-<math>[a,b]</math> ולכן היא חסומה, אזי לפי משפט בולצאנו | במקרה הראשון נניח שסדרת הפונקציות יורדת מונוטונית. לכן <math>\{f_n-f\}</math> היא סדרת פונקציות יורדת מונוטונית השואפת ל-0 ב-<math>[a,b]</math>. נסמן <math>g_n=f_n-f</math> (ולכן <math>g_n</math> חיובית) ונניח בשלילה שההתכנסות <math>g_n\to0</math> אינה במ"ש בקטע. לפיכך קיים <math>\varepsilon>0</math> כל שלכל <math>n_0\in\mathbb N</math> קיימים <math>n>n_0</math> ו-<math>x\in[a,b]</math> עבורם <math>g_n(x)>\varepsilon</math>. בפרט, עבור <math>n_0=1</math> קיימים <math>n_1>n_0</math> ו-<math>x_1\in[a,b]</math> כך ש-<math>g_{n_1}(x_1)>\varepsilon</math>. עבור <math>n_0=n_1+1</math> קיימים <math>n_2>n_0</math> ו-<math>x_2\in[a,b]</math> כך ש-<math>g_{n_2}(x_2)>\varepsilon</math> וכן הלאה. בדרך זו בונים תת סדרה <math>\{g_{n_k}\}</math> של <math>\{g_n\}</math> וסדרה <math>\{x_k\}</math> ב-<math>[a,b]</math> כך ש-<math>\forall k:\ g_{n_k}(x_k)>\varepsilon</math>. <math>\{x_k\}</math> נמצאת ב-<math>[a,b]</math> ולכן היא חסומה, אזי לפי משפט בולצאנו ויירשראס יש תת סדרה <math>\{x_{k_l}\}</math> מתכנסת, נאמר ל-<math>x_0\in[a,b]</math>. לפי הבנייה הנ"ל מתקיים <math>\forall l:\ g_{n_{k_l}}(x_{k_l})>\varepsilon</math> ומכיוון ש-<math>\lim_{l\to\infty} g_{n_{k_l}}(x_0)=0</math> קיים <math>l_0\in\mathbb N</math> כך שלכל <math>l>l_0</math> יתקיים <math>g_{n_{k_l}}(x_0)<\frac\varepsilon2</math>. <math>g_{n_{k_{l_0+1}}}</math> פונקציה רציפה שקטנה מ-<math>\frac\varepsilon2</math> ב-<math>x_0</math> ולכן יש סביבה S של <math>x_0</math> שבה <math>g_{n_{k_{l_0+1}}}</math> קטנה מ-<math>\varepsilon</math>. ה-<math>g_n</math> יורדות ולכן לכל <math>l>l_0</math> ולכל <math>x\in S</math> מתקיים <math>g_{n_{k_l}}(x)<\varepsilon</math>, אבל לפי הבנייה <math>x_{k_l}\to x_0</math> ולכן לכל l מספיק גדול מתקיים <math>g_{n_{k_l}}(x_{k_l})<\varepsilon</math>, בסתירה לכך שלכל l מתקיים <math>g_{n_{k_l}}(x_{k_l})>\varepsilon</math>. הסתירה מוכיחה את המשפט במקרה הזה. | ||
במקרה השני נניח שסדרת הפונקציות עולה מונוטונית. נסמן <math>g_n=-f_n</math> ולכן <math>\{g_n\}</math> יורדת ומתקיימים שאר תנאי המשפט, ולכן <math>g_n\to -f</math> במ"ש. מכאן ש-<math>f_n\to f</math> במ"ש והוכחנו גם את המקרה השני. {{משל}} | במקרה השני נניח שסדרת הפונקציות עולה מונוטונית. נסמן <math>g_n=-f_n</math> ולכן <math>\{g_n\}</math> יורדת ומתקיימים שאר תנאי המשפט, ולכן <math>g_n\to -f</math> במ"ש. מכאן ש-<math>f_n\to f</math> במ"ש והוכחנו גם את המקרה השני. {{משל}} | ||
=השתנות חסומה= | |||
פונקציה בעלת השתנות חסומה היא פונקציה שהשינוי שלה בציר ה-y הוא סופי | אינטואיטיבית, פונקציה בעלת השתנות חסומה היא פונקציה שהשינוי שלה בציר ה-y הוא סופי (הגדרה מדוייקת ניתן בהרצאה הבאה). | ||
===דוגמאות=== | ===דוגמאות=== | ||
| שורה 46: | שורה 42: | ||
* על <math>[1,\infty)</math> ההשתנות של <math>\frac1x</math> היא 1 כי הפונקציה ירדה מ-1 ל-0. | * על <math>[1,\infty)</math> ההשתנות של <math>\frac1x</math> היא 1 כי הפונקציה ירדה מ-1 ל-0. | ||
* לפונקציה <math>\sin\left(\frac1x\right)</math> ב-<math>(0,1)</math> יש השתנות אינסופית כי היא עלתה וירדה בין <math>\pm1</math> אינסוף פעמים. | * לפונקציה <math>\sin\left(\frac1x\right)</math> ב-<math>(0,1)</math> יש השתנות אינסופית כי היא עלתה וירדה בין <math>\pm1</math> אינסוף פעמים. | ||
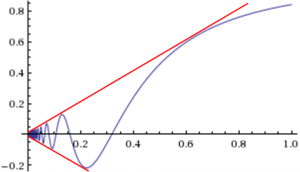
* [[קובץ:X sin(1 over x).png|ימין|300px|ממוזער|<div style="text-align:center;"><math>x\sin\left(\frac1x\right)</math></div>באדום: <math>y=\pm x</math>]]נגדיר <math>f(x)=x\sin\left(\frac1x\right)</math> בקטע <math>(0,1)</math>. האם יש לה השתנות חסומה? כאן יותר קשה לנחש מה ההשתנות כי מחד יש אינסוף עליות ומורדות, ומצד שני כאשר <math>x\to0^+</math> גם גדלי העליות והירידות שואפים ל-0. נוכיח שההשתנות אינה חסומה: לכל <math>n\in\mathbb N</math> | * [[קובץ:X sin(1 over x).png|ימין|300px|ממוזער|<div style="text-align:center;"><math>x\sin\left(\frac1x\right)</math></div>באדום: <math>y=\pm x</math>]]נגדיר <math>f(x)=x\sin\left(\frac1x\right)</math> בקטע <math>(0,1)</math>. האם יש לה השתנות חסומה? כאן יותר קשה לנחש מה ההשתנות כי מחד יש אינסוף עליות ומורדות, ומצד שני כאשר <math>x\to0^+</math> גם גדלי העליות והירידות שואפים ל-0. נוכיח שההשתנות אינה חסומה: לכל <math>n\in\mathbb N</math> יש לפונקציה נקודת קיצון ב-<math>\frac1{\pi n+\pi/2}</math>, וב-<math>\left[\tfrac1{\pi(n+1)+\pi/2},\tfrac1{\pi n+\pi/2}\right]</math> היא עולה או יורדת מהקו <math>y=\pm x</math> ל-<math>y=\mp x</math>, לכן ההשתנות שלה בקטע זה היא <math>\frac1{\pi(n+1)+\pi/2}+\frac1{\pi n+\pi/2}</math>, שגדול מ-<math>\frac2{\pi(n+1)+\pi/2}</math>. מכאן נובע שההשתנות הכוללת ב-<math>(0,1)</math> גדולה מ-<math>\sum_{n=1}^\infty \frac2{\pi(n+1)+\pi/2}=\infty</math>, ומכאן של-f אין השתנות חסומה ב-<math>(0,1)</math>. {{משל}} | ||
גרסה אחרונה מ־20:56, 29 ביולי 2012
את דוגמה 4 לא סיימנו בשיעור הקודם ולכן השלמנו זאת ב־31.5.11. חלק זה מופיע בסיכום השיעור הקודם ולא בדף הנוכחי.
טורי חזקות (המשך)
תזכורת: בהרצאה הקודמת הוכחנו ש-[math]\displaystyle{ \arctan(x)=\sum_{n=0}^\infty(-1)^n\frac{x^{2n+1}}{2n+1} }[/math] לכל [math]\displaystyle{ x\in(-1,1) }[/math] והערנו שאם ניתן להציב [math]\displaystyle{ x=1 }[/math] נקבל את המשוואה היפה [math]\displaystyle{ \frac\pi4=\sum_{n=0}^\infty\frac{(-1)^n}{2n+1} }[/math]. כמו כן אמרנו ש-[math]\displaystyle{ \ln(x)=\sum_{n=0}^\infty(-1)^n\frac{(x-1)^{n+1}}{n+1} }[/math] עבור [math]\displaystyle{ x\in(0,2) }[/math] ושאם מותר להציב [math]\displaystyle{ x=2 }[/math] אזי [math]\displaystyle{ \ln(2)=\sum_{n=0}^\infty\frac{(-1)^n}{n+1} }[/math].
משפט 5 (משפט אבל)
נניח ש-[math]\displaystyle{ f(x)=\sum_{n=0}^\infty a_nx^n }[/math] בקטע [math]\displaystyle{ (-1,1) }[/math] ו-[math]\displaystyle{ \sum_{n=0}^\infty a_n }[/math] מתכנס ל-[math]\displaystyle{ S\in\mathbb R }[/math], אזי [math]\displaystyle{ \lim_{x\to1^-}f(x) }[/math] קיים ושווה ל-S.
הוכחה
נעזר בסכימה בחלקים: נסמן [math]\displaystyle{ S_N=\sum_{n=0}^N a_n }[/math] ולכן [math]\displaystyle{ \forall N\in\mathbb N:\ \sum_{n=0}^Na_nx^n=\sum_{n=0}^{N-1}S_n\left(x^n-x^{n+1}\right)+S_Nx^N }[/math] כאשר [math]\displaystyle{ -1\lt x\lt 1 }[/math]. לפי הנתון [math]\displaystyle{ S=\lim_{N\to\infty}S_N }[/math], ולכן אם [math]\displaystyle{ 0\lt x\lt 1 }[/math] אז [math]\displaystyle{ \lim_{N\to\infty}S_Nx^N=0 }[/math] ועבור [math]\displaystyle{ 0\le x\le 1 }[/math] מתקיים [math]\displaystyle{ f(x)=\sum_{n=0}^\infty a_nx^n=\sum_{n=0}^\infty S_n\left(x^n-x^{n+1}\right)=(1-x)\sum_{n=0}^\infty S_nx^n }[/math]. כמו כן, [math]\displaystyle{ \forall x\in[0,1):\ 1=(1-x)\sum_{n=0}^\infty x^n }[/math] (כי [math]\displaystyle{ \frac1{1-x}=\sum_{n=0}^\infty x^n }[/math]). לכן [math]\displaystyle{ S=(1-x)\sum_{n=0}^\infty Sx^n }[/math] ומכאן שעבור [math]\displaystyle{ x\in[0,1) }[/math] מתקיים [math]\displaystyle{ f(x)-S=(1-x)\sum_{n=0}^\infty(S_n-S)x^n }[/math]. נרצה להוכיח ש-[math]\displaystyle{ \lim_{x\to1^-}f(x)-S=0 }[/math]: יהי [math]\displaystyle{ \varepsilon\gt 0 }[/math] נתון ומכיוון ש-[math]\displaystyle{ \lim_{n\to\infty}S_n=S }[/math] קיים [math]\displaystyle{ n_0\in\mathbb N }[/math] כך שלכל [math]\displaystyle{ n\gt n_0 }[/math] יתקיים [math]\displaystyle{ |S_n-S|\lt \frac\varepsilon2 }[/math]. נסמן [math]\displaystyle{ I_1=(1-x)\sum_{n=0}^{n_0}(S_n-S)x^n }[/math] וכן [math]\displaystyle{ I_2=(1-x)\sum_{n=n_0+1}^\infty(S_n-S)x^n }[/math], לכן [math]\displaystyle{ f(x)-S=I_1+I_2 }[/math]. עתה [math]\displaystyle{ |I_2|\le(1-x)\sum_{n=n_0+1}^\infty|S_n-S|x^n\lt \frac\varepsilon2(1-x)\sum_{n=n_0+1}^\infty x^n\le\frac\varepsilon2(1-x)\sum_{n=0}^\infty x^n=\frac\varepsilon2 }[/math]. לגבי [math]\displaystyle{ I_1 }[/math] נגדיר [math]\displaystyle{ M=\sum_{n=0}^{n_0}|S_n-S| }[/math] ולכן [math]\displaystyle{ |I_1|\le(1-x)\sum_{n=0}^{n_0}|S_n-S| }[/math]. עתה [math]\displaystyle{ x\to1^- }[/math] ולכן [math]\displaystyle{ 0\lt 1-x\lt \frac\varepsilon{2M} }[/math], לכן [math]\displaystyle{ |I_1|\le\frac\varepsilon{2M}M=\frac\varepsilon2 }[/math]. לסיכום הוכחנו שאם [math]\displaystyle{ 1-\frac\varepsilon{2M}\lt x\lt 1 }[/math] אזי [math]\displaystyle{ |f(x)-S|\lt |I_1|+|I_2|\lt \varepsilon }[/math] ולכן [math]\displaystyle{ \lim_{x\to1^-}f(x)-S=0 }[/math]. [math]\displaystyle{ \blacksquare }[/math]
מסקנה
לגבי טור חזקות כללי [math]\displaystyle{ f(x)=\sum_{n=0}^\infty a_n(x-x_0)^n }[/math] בעל רדיוס התכנסות R:
- אם [math]\displaystyle{ \sum_{n=0}^\infty a_nR^n }[/math] מתכנס ל-S אזי [math]\displaystyle{ \lim_{x\to x_0+R^-}f(x) }[/math] קיים ושווה ל-S.
- אם [math]\displaystyle{ \sum_{n=0}^\infty a_n(-R)^n }[/math] מתכנס ל-T אזי [math]\displaystyle{ \lim_{x\to(x_0-R)^+}f(x) }[/math] קיים ושווה ל-T.
הוכחה
- נציב [math]\displaystyle{ y=\frac{x-x_0}R }[/math] ולכן [math]\displaystyle{ f(x)=\sum_{n=0}^\infty \left(a_nR^n\right)y^n }[/math] עבור [math]\displaystyle{ |x-x_0|\lt R }[/math], כלומר עבור [math]\displaystyle{ |y|\lt 1 }[/math]. נגדיר [math]\displaystyle{ g(y)=f(x) }[/math] ולכן מתקיימים תנאי משפט אבל ומתקיים [math]\displaystyle{ \lim_{y\to1^-}g(y)=S }[/math], לכן [math]\displaystyle{ \lim_{x\to x_0+R^-}f(x)=S }[/math]. [math]\displaystyle{ \blacksquare }[/math]
- נציב [math]\displaystyle{ y=\frac{x-x_0}{-R} }[/math] ונוכיח כמו בסעיף 1. [math]\displaystyle{ \blacksquare }[/math]
משפט 6 (משפט דיני)
נניח שלכל n [math]\displaystyle{ f_n }[/math] רציפה ב-[math]\displaystyle{ [a,b] }[/math] ונניח שסדרת הפונקציות מונוטונית, כלומר לכל [math]\displaystyle{ x\in[a,b] }[/math] הסדרה [math]\displaystyle{ \{f_n(x)\}_{n=1}^\infty }[/math] עולה או לכל [math]\displaystyle{ x\in[a,b] }[/math] הסדרה [math]\displaystyle{ \{f_n(x)\}_{n=1}^\infty }[/math] יורדת. כמו כן ידוע כי [math]\displaystyle{ f_n\to f }[/math] ו-f רציפה ב-[math]\displaystyle{ [a,b] }[/math], אזי ההתכנסות במ"ש.
הסבר
לפני ההוכחה נסביר למה צריך את כל הנתונים:
- אם הקטע פתוח במקום סגור, נבחר את הקטע [math]\displaystyle{ (0,1) }[/math] ואת סדרת הפונקציות [math]\displaystyle{ f_n(x)=x^n }[/math]. ברור כי כל הפונקציות רציפות בקטע וסדרת הפונקציות מונוטונית, וכן הפונקציה הגבולית היא הפונקציה הרציפה [math]\displaystyle{ f(x)=0 }[/math], אבל כבר הוכחנו בעבר שההתכנסות אינה במ"ש.
- בקטע סגור [math]\displaystyle{ [0,1] }[/math] נבחר באותה סדרת פונקציות. הפונקציה הגבולית היא [math]\displaystyle{ f(x)=\begin{cases}0&0\le x\lt 1\\1&x=1\end{cases} }[/math] שאינה רציפה, ואכן ההתכנסות אינה במ"ש.
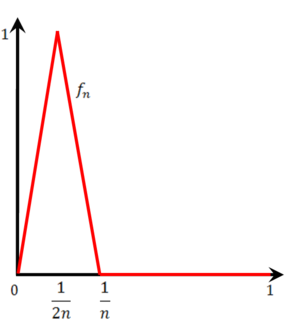
- נגדיר סדרת פונקציות לפי הגרף שמשמאל. כל [math]\displaystyle{ f_n }[/math] רציפה ב-[math]\displaystyle{ [0,1] }[/math] והן מתכנסות לפונקציה הרציפה 0, אבל סדרת הפונקציות לא מונוטונית, ואכן ההתכנסות אינה במ"ש.
- נגדיר [math]\displaystyle{ f_n(x)=\begin{cases}x^n&0\le x\lt 1\\0&x=1\end{cases} }[/math] ולכן סדרת הפונקציות מונוטונית אבל הפונקציות אינן רציפות, ואכן, למרות שהפונקציה הגבולית 0 רציפה, ההתכנסות אינה במ"ש.
הוכחה
במקרה הראשון נניח שסדרת הפונקציות יורדת מונוטונית. לכן [math]\displaystyle{ \{f_n-f\} }[/math] היא סדרת פונקציות יורדת מונוטונית השואפת ל-0 ב-[math]\displaystyle{ [a,b] }[/math]. נסמן [math]\displaystyle{ g_n=f_n-f }[/math] (ולכן [math]\displaystyle{ g_n }[/math] חיובית) ונניח בשלילה שההתכנסות [math]\displaystyle{ g_n\to0 }[/math] אינה במ"ש בקטע. לפיכך קיים [math]\displaystyle{ \varepsilon\gt 0 }[/math] כל שלכל [math]\displaystyle{ n_0\in\mathbb N }[/math] קיימים [math]\displaystyle{ n\gt n_0 }[/math] ו-[math]\displaystyle{ x\in[a,b] }[/math] עבורם [math]\displaystyle{ g_n(x)\gt \varepsilon }[/math]. בפרט, עבור [math]\displaystyle{ n_0=1 }[/math] קיימים [math]\displaystyle{ n_1\gt n_0 }[/math] ו-[math]\displaystyle{ x_1\in[a,b] }[/math] כך ש-[math]\displaystyle{ g_{n_1}(x_1)\gt \varepsilon }[/math]. עבור [math]\displaystyle{ n_0=n_1+1 }[/math] קיימים [math]\displaystyle{ n_2\gt n_0 }[/math] ו-[math]\displaystyle{ x_2\in[a,b] }[/math] כך ש-[math]\displaystyle{ g_{n_2}(x_2)\gt \varepsilon }[/math] וכן הלאה. בדרך זו בונים תת סדרה [math]\displaystyle{ \{g_{n_k}\} }[/math] של [math]\displaystyle{ \{g_n\} }[/math] וסדרה [math]\displaystyle{ \{x_k\} }[/math] ב-[math]\displaystyle{ [a,b] }[/math] כך ש-[math]\displaystyle{ \forall k:\ g_{n_k}(x_k)\gt \varepsilon }[/math]. [math]\displaystyle{ \{x_k\} }[/math] נמצאת ב-[math]\displaystyle{ [a,b] }[/math] ולכן היא חסומה, אזי לפי משפט בולצאנו ויירשראס יש תת סדרה [math]\displaystyle{ \{x_{k_l}\} }[/math] מתכנסת, נאמר ל-[math]\displaystyle{ x_0\in[a,b] }[/math]. לפי הבנייה הנ"ל מתקיים [math]\displaystyle{ \forall l:\ g_{n_{k_l}}(x_{k_l})\gt \varepsilon }[/math] ומכיוון ש-[math]\displaystyle{ \lim_{l\to\infty} g_{n_{k_l}}(x_0)=0 }[/math] קיים [math]\displaystyle{ l_0\in\mathbb N }[/math] כך שלכל [math]\displaystyle{ l\gt l_0 }[/math] יתקיים [math]\displaystyle{ g_{n_{k_l}}(x_0)\lt \frac\varepsilon2 }[/math]. [math]\displaystyle{ g_{n_{k_{l_0+1}}} }[/math] פונקציה רציפה שקטנה מ-[math]\displaystyle{ \frac\varepsilon2 }[/math] ב-[math]\displaystyle{ x_0 }[/math] ולכן יש סביבה S של [math]\displaystyle{ x_0 }[/math] שבה [math]\displaystyle{ g_{n_{k_{l_0+1}}} }[/math] קטנה מ-[math]\displaystyle{ \varepsilon }[/math]. ה-[math]\displaystyle{ g_n }[/math] יורדות ולכן לכל [math]\displaystyle{ l\gt l_0 }[/math] ולכל [math]\displaystyle{ x\in S }[/math] מתקיים [math]\displaystyle{ g_{n_{k_l}}(x)\lt \varepsilon }[/math], אבל לפי הבנייה [math]\displaystyle{ x_{k_l}\to x_0 }[/math] ולכן לכל l מספיק גדול מתקיים [math]\displaystyle{ g_{n_{k_l}}(x_{k_l})\lt \varepsilon }[/math], בסתירה לכך שלכל l מתקיים [math]\displaystyle{ g_{n_{k_l}}(x_{k_l})\gt \varepsilon }[/math]. הסתירה מוכיחה את המשפט במקרה הזה.
במקרה השני נניח שסדרת הפונקציות עולה מונוטונית. נסמן [math]\displaystyle{ g_n=-f_n }[/math] ולכן [math]\displaystyle{ \{g_n\} }[/math] יורדת ומתקיימים שאר תנאי המשפט, ולכן [math]\displaystyle{ g_n\to -f }[/math] במ"ש. מכאן ש-[math]\displaystyle{ f_n\to f }[/math] במ"ש והוכחנו גם את המקרה השני. [math]\displaystyle{ \blacksquare }[/math]
השתנות חסומה
אינטואיטיבית, פונקציה בעלת השתנות חסומה היא פונקציה שהשינוי שלה בציר ה-y הוא סופי (הגדרה מדוייקת ניתן בהרצאה הבאה).
דוגמאות
- ההשתנות הכללית של [math]\displaystyle{ \sin }[/math] בקטע [math]\displaystyle{ \left[0,\tfrac32\pi\right] }[/math] היא 3 (ובפרט היא חסומה) כי הפונקציה עלתה 1 וירדה 2.
- על [math]\displaystyle{ [1,\infty) }[/math] ההשתנות של [math]\displaystyle{ \frac1x }[/math] היא 1 כי הפונקציה ירדה מ-1 ל-0.
- לפונקציה [math]\displaystyle{ \sin\left(\frac1x\right) }[/math] ב-[math]\displaystyle{ (0,1) }[/math] יש השתנות אינסופית כי היא עלתה וירדה בין [math]\displaystyle{ \pm1 }[/math] אינסוף פעמים.
- נגדיר [math]\displaystyle{ f(x)=x\sin\left(\frac1x\right) }[/math] בקטע [math]\displaystyle{ (0,1) }[/math]. האם יש לה השתנות חסומה? כאן יותר קשה לנחש מה ההשתנות כי מחד יש אינסוף עליות ומורדות, ומצד שני כאשר [math]\displaystyle{ x\to0^+ }[/math] גם גדלי העליות והירידות שואפים ל-0. נוכיח שההשתנות אינה חסומה: לכל [math]\displaystyle{ n\in\mathbb N }[/math] יש לפונקציה נקודת קיצון ב-[math]\displaystyle{ \frac1{\pi n+\pi/2} }[/math], וב-[math]\displaystyle{ \left[\tfrac1{\pi(n+1)+\pi/2},\tfrac1{\pi n+\pi/2}\right] }[/math] היא עולה או יורדת מהקו [math]\displaystyle{ y=\pm x }[/math] ל-[math]\displaystyle{ y=\mp x }[/math], לכן ההשתנות שלה בקטע זה היא [math]\displaystyle{ \frac1{\pi(n+1)+\pi/2}+\frac1{\pi n+\pi/2} }[/math], שגדול מ-[math]\displaystyle{ \frac2{\pi(n+1)+\pi/2} }[/math]. מכאן נובע שההשתנות הכוללת ב-[math]\displaystyle{ (0,1) }[/math] גדולה מ-[math]\displaystyle{ \sum_{n=1}^\infty \frac2{\pi(n+1)+\pi/2}=\infty }[/math], ומכאן של-f אין השתנות חסומה ב-[math]\displaystyle{ (0,1) }[/math]. [math]\displaystyle{ \blacksquare }[/math]