חדוא 1 - ארז שיינר

88-132 חשבון אינפיניטיסימלי 1

סרטוני ותקציר ההרצאות

פרק 1 - מספרים וחסמים

קבוצות מספרים

• הטבעיים $\mathbb{N}=\{1,2,3,...\}$
• השלמים $\mathbb{Z}=\{0,-1,1,-2,2,...\}$
• הרציונאליים $\mathbb{Q}=\{\frac{p}{n}|p\in \mathbb{Z},n\in \mathbb{N}\}$
• הממשיים $\mathbb{R}$, כל השברים העשרוניים כולל האינסופיים

• העשרה: בנייה של שדה הממשיים באמצעות חתכי דדקינד

• לא קיים $x\in \mathbb{Q}$ כך ש $x^2=2$.
• במילים פשוטות, $\sqrt{2}$ אינו רציונאלי (בהמשך נוכיח שיש מספר ממשי כזה).

חסמים

• תהי $A\subseteq \mathbb{R}$ אזי:
  • $M\in \mathbb{A}$ נקרא המקסימום של A או האיבר הגדול ביותר של A אם לכל $a\in A$ מתקיים כי $a\le M$
  • $M\in \mathbb{R}$ נקרא חסם מלעיל של A אם לכל $a\in A$ מתקיים כי $a\le M$
  • $m\in \mathbb{A}$ נקרא המינימום של A או האיבר הקטן ביותר של A אם לכל $a\in A$ מתקיים כי $a\ge M$
  • $m\in \mathbb{R}$ נקרא חסם מלרע של A אם לכל $a\in A$ מתקיים כי $a\ge M$

• כמו כן:
  • אם יש איבר קטן ביותר בקבוצת חסמי המלעיל של A הוא נקרא החסם העליון של A, או הסופרמום של A ומסומן $sup(A)$
  • אם יש איבר גדול ביותר בקבוצת חסמי המלרע של A הוא נקרא החסם התחתון של A, או האינפימום של A ומסומן $inf(A)$

• בשדה הממשיים לכל קבוצה לא ריקה וחסומה מלעיל יש חסם עליון, ולכל קבוצה לא ריקה וחסומה מלרע יש חסם תחתון.
• בשדה הרציונאליים זה לא נכון; לקבוצה $A=\{x\in \mathbb{Q}|x^2<2\}$ אין מספר רציונאלי קטן ביותר מבין חסמי המלעיל שלה.

• תהי $A\subseteq \mathbb{R}$ ויהי $M\in \mathbb{R}$ אזי:
  • M הוא החסם העליון של A אם ורק אם M הוא חסם מלעיל של A ולכל מספר $M-\epsilon <M$ קיים מספר $a\in A$ כך ש $a>M-\epsilon$
  • m הוא החסם התחתון של A אם ורק אם m הוא חסם מלרע של A ולכל מספר $m<m+\epsilon$ קיים מספר $a\in A$ כך ש $a<m+\epsilon$

• דוגמא: תהיינה $\mathrm{\varnothing }\ne A,B\subseteq \mathbb{R}$ חסומות מלעיל כך שA אינה מכילה חסמי מלעיל של B, אזי $sup(A)\le sup(B)$

פרק 2 - סדרות

הגדרת הגבול

• הגדרת הגבול של סדרה:
• תהי סדרה ממשית $a_n$ ויהי מספר ממשי $L\in \mathbb{R}$.
• $L$ הינו גבול הסדרה $a_n$ (מסומן $lim{a}_n=L$ או $a_n\to L$) אם:
  • לכל סביבה של הגבול, קיים מקום בסדרה שאחריו כל איברי הסדרה נמצאים בסביבה הנתונה, כלומר:
  • לכל מרחק $\epsilon >0$ קיים מקום $N\in \mathbb{N}$ כך שאחריו לכל $n>N$ מתקיים כי $|a_n-L|<\epsilon$

• נגדיר ש$a_n\to \mathrm{\infty }$ אם לכל $M>0$ קיים $N\in \mathbb{N}$ כך שלכל $n>N$ מתקיים כי $a_n>M$
• נגדיר ש$a_n\to -\mathrm{\infty }$ אם $-a_n\to \mathrm{\infty }$

• טענה: תהי $a_n\to \mathrm{\infty }$ אזי $\frac{1}{a_n}\to 0$
• טענה: תהי $0\ne a_n\to 0$ אזי $\frac{1}{|a_n|}\to \mathrm{\infty }$

• הגבול הוא יחיד
• מספר סופי של איברים לא משפיע על הגבול
• סדרה מתכנסת במובן הצר חסומה

מבוא לחשבון גבולות (אריתמטיקה של גבולות)

• (אי שיוויון המשולש.)
• סכום.
• מכפלה.
• חלוקה.

כלים לחישוב גבולות

• סנדביץ' וחצי סדנביץ'
• $a_n\to 0⟺|a_n|\to 0$
• חסומה כפול אפיסה היא אפיסה.
• מבחן המנה (הוכחה בסיכום הבא על אי-שוויון הממוצעים).
  • תהי סדרה $a_n$ המקיימת כי גבול המנה הוא $\left|\frac{a_{n+1}}{a_n}\right|\to L$ אזי:
    • אם $1<L\le \mathrm{\infty }$ מתקיים כי $|a_n|\to \mathrm{\infty }$
    • אם $0\le L<1$ מתקיים כי $a_n\to 0$
    • מתקיים כי $\sqrt[n]{|a_n|}\to L$

• דוגמא:
  • $\sqrt[n]{n}\to 1$

• אינדוקציה.
• ברנולי - אקספוננט חיובי שואף לאפס, אחד או אינסוף.

חשבון גבולות (אריתמטיקה של גבולות)

• אריתמטיקה מורחבת (הכתיב הוא מקוצר ואינו מדוייק):
  • חסומה כפול אפיסה = אפיסה
  • חסומה חלקי אינסוף = אפיסה
  • $\mathrm{\infty }+\mathrm{\infty }=\mathrm{\infty }$
  • $\mathrm{\infty }\cdot \mathrm{\infty }=\mathrm{\infty }$
  • ${\mathrm{\infty }}^{\mathrm{\infty }}=\mathrm{\infty }$
  • $\frac{1}{0}\ne \mathrm{\infty }$
  • $\frac{1}{0^{+}}=\mathrm{\infty }$
  • $0^{\mathrm{\infty }}=0$
  • אינסוף כפול סדרה השואפת למספר חיובי = אינסוף.
  • אינסוף כפול סדרההשואפת למספר שלילי = אינסוף.
  • יש גבול סופי + אין גבול סופי = אין גבול סופי.
  • אינסוף ועוד חסומה שווה אינסוף.
  • אם $a>1$ אזי $a^{\mathrm{\infty }}=\mathrm{\infty }$
  • חזקת סדרות שואפת לחזקת הגבולות.

המקרים הבעייתיים

• המקרים הבעייתיים בהם צריך להפעיל מניפולציות אלגבריות או משפטים על מנת לחשב את הגבול:
  • $\frac{0}{0},\frac{\mathrm{\infty }}{\mathrm{\infty }},0\cdot \mathrm{\infty },\mathrm{\infty }-\mathrm{\infty },0^0,{\mathrm{\infty }}^0,1^{\mathrm{\infty }}$

סדרות מונוטוניות והמספר e

• כל סדרה מונוטונית הינה חסומה מתכנסת לגבול סופי, או שאינה חסומה ושואפת לגבול אינסופי.
• המספר e (הוכחות בעזרת אי-שוויון הממוצעים).
• $2<e<4$.
• אם $a_n\to \mathrm{\infty }$ אזי ${(1+\frac{1}{a_n})}^{a_n}\to e$
  • $[a_n]\le a_n\le [a_n]+1$, כאשר $[a_n]$ הוא המספר השלם הגדול ביותר שקטן או שווה ל$a_n$.
  • ${(1+\frac{1}{[a_n]+1})}^{[a_n]}\le {(1+\frac{1}{a_n})}^{a_n}\le {(1+\frac{1}{[a_n]})}^{[a_n]+1}$
  • שני הצדדים שואפים לe ולכן לפי כלל הסנדוויץ הסדרה אכן שואפת לe.
• אם $a_n\to -\mathrm{\infty }$ אזי ${(1+\frac{1}{a_n})}^{a_n}\to e$
  • ראשית ${(1-\frac{1}{n})}^n\to \frac{1}{e}$ (הוכחה בקישור לערך על המספר e).
  • כעת חזקה שלילית הופכת את השבר, וניתן לסיים את ההוכחה באופן דומה להוכחה במקרה הקודם.

• אם $a_n\to 1$ אזי $a_n^{b_n}\to e^{lim{b}_n\cdot (a_n-1)}$
  • $a_n^{b_n}={\left[{(1+(a_n-1))}^{\frac{1}{a_n-1}}\right]}^{b_n\cdot (a_n-1)}$.
  • ${(1+(a_n-1))}^{\frac{1}{a_n-1}}\to e$ בין אם $a_n-1$ שלילי או חיובי, לפי הטענות לעיל.
  • שימו לב שאם $a_n=1$, אז ממילא מקבלים 1 בנוסחא הסופית, ואז לא צריך לחלק ב$a_n-1$ ששווה אפס.

• דוגמא:
  • $lim{\left(\frac{n+1}{n-2}\right)}^n=e^{limn\cdot (\frac{n+1}{n-2}-1)}=e^{lim\frac{3n}{n-2}}=e^3$

פרק 4 - פונקציות ורציפות

מבוא לגבולות

• מבוא לגבולות (שיטות אלגבריות: כפל בצמוד, הוצאת חזקה משמעותית).
  • $\underset{x\to 2}{lim}\frac{x^2-4}{x-2}$
  • $\underset{x\to \mathrm{\infty }}{lim}\frac{2x^2+5x+3}{3x^2-100}$
  • $\underset{x\to \mathrm{\infty }}{lim}\sqrt{x^2+1}-x$
  • $\underset{x\to \mathrm{\infty }}{lim}\sqrt{x^2+x+1}-x$
  • $\underset{x\to \mathrm{\infty }}{lim}{x}^2-x$

הפונקציות הטריגונומטריות

• הגדרת סינוס וקוסינוס ע"י מעגל היחידה.
  • $si{n}^2(x)+co{s}^2(x)=1$
  • $sin(-x)=-sin(x),cos(-x)=cos(x)$
  • $sin(a+b)=sin(a)cos(b)+sin(b)cos(a),cos(a+b)=cos(a)cos(b)-sin(a)sin(b)$
  • $sin(2x)=2sin(x)cos(x),cos(2x)=co{s}^2(x)-si{n}^2(x)$

• 
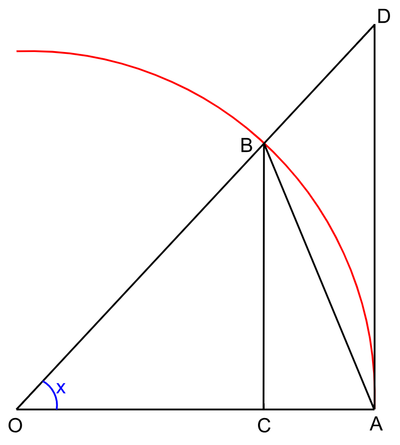
  • עבור זוית $0<x<\frac{\pi }{2}$ שטח המשולש חסום בשטח הגזרה (משולש פיצה עם הקשה) שחסום בשטח המשולש:
  • $S_{\mathrm{△}AOB}<S_{◯AOB}<S_{\mathrm{△}AOD}$
  • $\frac{sin(x)}{2}<\frac{x}{2}<\frac{tan(x)}{2}$
    • כיוון ש$0<sin(x)<x$ בתחום $(0,\frac{\pi }{2})$, נובע לפי סנדוויץ' ש$\underset{x\to 0^{+}}{lim}sin(x)=0$.
    • כיוון שמדובר בפונקציה אי זוגית, נובע שזה גם הגבול משני הצדדים.
    • כעת בתחום $(-\frac{\pi }{2},\frac{\pi }{2})$ הקוסינוס חיובית ולכן $cos(x)=\sqrt{1-si{n}^2(x)}$ ונובע כי $\underset{x\to 0}{lim}cos(x)=1$.
  • נחלק את אי השיוויון הטריגונומטרי בסינוס ונקבל:
  • $1<\frac{x}{sin(x)}<\frac{1}{cos(x)}$
  • לפי כלל הסנדביץ $\underset{x\to 0^{+}}{lim}\frac{sin(x)}{x}=1$
  • כיוון שמדובר בפונקציה זוגית, נובע שהגבול משני הצדדים שווה 1.

• ראינו ש$\underset{x\to 0}{lim}\frac{sin(x)}{x}=1$.
• שימו לב ש$\underset{x\to \mathrm{\infty }}{lim}\frac{sin(x)}{x}=0$, כיוון שמדובר בחסומה חלקי שואפת לאינסוף.

רציפות

• גבול של הרכבת פונקציות נכשל ללא רציפות.
  • $f(x)=\frac{x}{x},g(x)=0$ מתקיים כי $\underset{x\to 0}{lim}f(x)=1,\underset{x\to 2}{lim}g(x)=0$ אבל $\underset{x\to 2}{lim}f(g(x))\ne 1$.
• רציפות.
• טענה: אם f רציפה ב$x_0$ אזי לכל סדרה $x_n\to x_0$ (גם אם אינה שונה מ$x_0$) מתקיים כי $f(x_n)\to f(x_0)$.
• הרכבת רציפות: תהי f רציפה ב$x_0$ ותהי g רציפה ב$f(x_0)$. אזי $g\circ f$ רציפה ב$x_0$.
  • הוכחה:
  • תהי סדרה $x_0\ne x_n\to x_0$ אזי $f(x_n)\to f(x_0)$
  • לפי הטענה הקודמת, $g(f(x_n))\to g(f(x_0))$.

• מיון אי רציפות.
  • רציפות - הגבול בנקודה שווה לערך בנקודה.
  • סליקה - הגבול קיים וסופי בנקודה, אך שונה מהערך בנקודה או שהפונקציה אינה מוגדרת בנקודה.
  • קפיצתית (מין ראשון) - הגבולות החד צדדיים קיימים סופיים ושונים בנקודה.
  • עיקרית (מין שני) - אחד הגבולות החד צדדיים אינו קיים או שאינו סופי.