חתכי דדקינד: הבדלים בין גרסאות בדף
אין תקציר עריכה |
|||
| (44 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 31: | שורה 31: | ||
**<math>A</math> חסומה מלעיל. | **<math>A</math> חסומה מלעיל. | ||
**לכל <math>m\in\mathbb{Q}</math> מתקיים כי <math>m\notin A</math> אם ורק אם <math>m</math> חסם מלעיל של <math>A</math> | **לכל <math>m\in\mathbb{Q}</math> מתקיים כי <math>m\notin A</math> אם ורק אם <math>m</math> חסם מלעיל של <math>A</math> | ||
*הערות ותזכורות: | *הערות ותזכורות: | ||
**חסם מלעיל של קבוצה הוא מספר שגדול יותר מכל איברי הקבוצה. | **חסם מלעיל של קבוצה הוא מספר שגדול יותר מכל איברי הקבוצה. | ||
**בחתך דדקינד אין מספר גדול ביותר, אחרת זה היה חסם מלעיל ששיך לקבוצה. | **בחתך דדקינד אין מספר גדול ביותר, אחרת זה היה חסם מלעיל ששיך לקבוצה. זה משול לחצי האבוקדו ללא הגרעין. | ||
**בחתך המייצג מספר שאינו רציונאלי, כמו שורש שתיים, גם במשלים של החתך אין מספר קטן ביותר, זה משול לשני חצאי אבוקדו ללא גרעין כלל. | |||
**אם מספר שייך לחתך, בוודאי כל מספר נמוך ממנו שייך לחתך הרי לא ייתכן שמספר נמוך ממנו הוא חסם מלעיל. | **אם מספר שייך לחתך, בוודאי כל מספר נמוך ממנו שייך לחתך הרי לא ייתכן שמספר נמוך ממנו הוא חסם מלעיל. | ||
| שורה 43: | שורה 45: | ||
*כאשר נגדיר את הפעולות, נזכור שמטרתינו היא להגדיר את הנקודות "החסרות" על הציר. | *כאשר נגדיר את הפעולות, נזכור שמטרתינו היא להגדיר את הנקודות "החסרות" על הציר. | ||
== | ==חיבור חתכי דדקינד== | ||
*יהיו שתי חתכים <math>A,B</math>, נגדיר את החיבור: | *יהיו שתי חתכים <math>A,B</math>, נגדיר את החיבור: | ||
| שורה 56: | שורה 56: | ||
**יהי <math>a+b\in A+B</math>, כיוון שאיברי החתכים אינם חסמי מלעיל, קיימים <math>a<c\in A</math> וכן <math>b<d\in B</math> ולכן <math>a+b<c+d\in A+B</math> ו<math>a+b</math> אינו חסם מלעיל של <math>A+B</math> | **יהי <math>a+b\in A+B</math>, כיוון שאיברי החתכים אינם חסמי מלעיל, קיימים <math>a<c\in A</math> וכן <math>b<d\in B</math> ולכן <math>a+b<c+d\in A+B</math> ו<math>a+b</math> אינו חסם מלעיל של <math>A+B</math> | ||
**יהי <math>m\in\mathbb{Q}</math> שאינו חסם מלעיל של <math>A+B</math>, לכן קיימים <math>m<a+b\in A+B</math>. כעת <math>m-a<b</math> כלומר <math>m-a</math> אינו חסם מלעיל של B ולכן שייך לקבוצה. סה"כ <math>m=a+(m-a)\in A+B</math>. | **יהי <math>m\in\mathbb{Q}</math> שאינו חסם מלעיל של <math>A+B</math>, לכן קיימים <math>m<a+b\in A+B</math>. כעת <math>m-a<b</math> כלומר <math>m-a</math> אינו חסם מלעיל של B ולכן שייך לקבוצה. סה"כ <math>m=a+(m-a)\in A+B</math>. | ||
===חתך האפס=== | |||
*נגדיר את חתך האפס: | |||
**<math>0_D=\left\{x\in\mathbb{Q}|x<0\right\}</math> | |||
*נוכיח כי חתך האפס נייטרלי לחיבור: | |||
**יהי חתך דדקינד <math>A</math> צריך להוכיח כי <math>A+0_D=A</math> | |||
**נבצע הכלה דו כיוונית. בכיוון הראשון: | |||
***יהי <math>x=a+h\in A+0_D</math> צריך להוכיח כי <math>x\in A</math> | |||
***כיוון ש <math>h\in 0_D</math> נובע לפי ההגדרה כי <math>h<0</math> ולכן <math>a+h<a</math> | |||
***לכן <math>x=a+h</math> אינו חסם מלעיל של <math>A</math> ולכן <math>x\in A</math> | |||
**בכיוון השני: | |||
***יהי <math>a\in A</math> צריך להוכיח כי <math>a\in A+0_D</math> | |||
***אמרנו כי בחתך דדקינד אין איבר גדול ביותר, ולכן קיים <math>a<b\in A</math> | |||
***כיוון ש <math>a-b<0</math> נובע כי <math>a-b\in 0_D</math> | |||
***סה"כ <math>a=b+(a-b)\in A+0_D</math> כפי שרצינו. | |||
===נגדי=== | |||
*יהי חתך A, נגדיר את הנגדי: | |||
**<math>-A=\left\{x\in\mathbb{Q}|\exists m\notin A:x<-m\right\}</math> | |||
*לדוגמא <math>-\left\{x\in\mathbb{Q}|x<2\right\}=\left\{x\in\mathbb{Q}|x<-2\right\}</math> | |||
[[קובץ:negDedekind2.png|1000px]] | |||
*הנגדי הוא חתך דדקינד בעצמו: | |||
**הנגדי לא ריק: | |||
***כיוון שA חסומה מלעיל יש לה חסם, וכל המספרים שקטנים ממינוס החסם שייכים לנגדי, ולכן <math>-A\neq\emptyset</math> | |||
**הנגדי חסום מלעיל: | |||
***יהי <math>a\in A</math> לכן לכל <math>m\notin A</math> מתקיים כי <math>a<m</math> ולכן <math>-m<-a</math> | |||
***לכל <math>x\in -A</math> קיים <math>m\notin A</math> כך ש <math>x<-m</math> ולכן <math>x<-a</math> | |||
***בעצם הנגדי של כל איבר בA הוא חסם מלעיל של <math>-A</math>. | |||
**כל איבר בנגדי אינו חסם מלעיל: | |||
***לכל איבר בנגדי <math>x<-m</math> לכן אמצע הקטע בין <math>x,-m</math> גדול מ<math>x</math> וקטן מ<math>-m</math> ולכן שייך לנגדי <math>-A</math> ולכן <math>x</math> אינו חסם מלעיל. | |||
**אם איבר אינו חסם מלעיל, הוא שייך לנגדי: | |||
***נניח <math>y</math> אינו חסם מלעיל של <math>-A</math> לכן קיים <math>y<x\in -A</math> ולכן קיים <math>m\notin A</math> כך ש <math>y<x<-m</math> ולכן <math>y\in -A</math> | |||
====הוכחה שאכן מדובר באיבר נגדי==== | |||
*יהי חתך <math>A</math> צריך להוכיח כי <math>A+(-A)=0_D</math> | |||
*נבצע הכלה דו כיוונית | |||
*בכיוון ראשון: | |||
**יהי <math>x+y\in (A+(-A))</math>. | |||
**כיוון ש<math>y\in (-A)</math> קיים <math>m\not\in A</math> כך ש <math>y<-m</math> | |||
**לכן <math>x+y<m+y<0</math> | |||
**לכן <math>x+y\in 0_D</math> | |||
*בכיוון שני: | |||
**יהי <math>t\in 0_D</math> כלומר <math>t<0</math> | |||
**רוצים למצוא <math>a\in A, b\in (-A)</math> כך ש <math>a+b=t</math> | |||
**נבחר <math>m\not\in A</math> כך ש<math>m+\frac{t}{2}\in A</math> | |||
***מדוע זה אפשרי? כי אם <math>m+\frac{t}{2}\not\in A</math> אז זה חסם, ואפשר להוסיף לו <math>\frac{t}{2}</math> שזה מספר שלילי. אחרי מספיק פעמים נהיה קטנים מאיבר בקבוצה | |||
**כעת <math>-m+\frac{t}{2}<-m</math> ולכן <math>-m+\frac{t}{2}\in (-A)</math>. | |||
**סה"כ <math>t=(m+\frac{t}{2})+(-m+\frac{t}{2})\in A+(-A)</math> | |||
==יחס סדר== | |||
*יחס ההכלה הוא יחס סדר לינארי (מלא) על קבוצת חתכי דדקינד | |||
*הוכחה: | |||
**יהיו שני חתכים A,B. | |||
**אם קיים <math>m\notin A</math> חסם מלעיל של A כך ש<math>m\in B</math> אזי כל איבר של A אינו חסם מלעיל של B ולכן שייך לB, כלומר <math>A\subseteq B</math> | |||
**אחרת, לכל <math>m\notin A</math> מתקיים כי <math>m\notin B</math>. כלומר <math>\overline{A}\subseteq\overline{B}</math> ולכן <math>B\subseteq A</math> | |||
*נגדיר את החתכים החיוביים להיות כל החתכים A כך ש<math>0_D < A</math> ונגדיר את החתכים השליליים על ידי <math>0_D > A</math> | |||
*טענה: <math>A\geq 0_D</math> אם ורק אם <math>-A\leq 0_D</math> | |||
*הוכחה: | |||
** ראשית נניח כי <math>A\geq 0_D</math> | |||
***כלומר בעצם <math>0_D\subseteq A</math> ולכן לכל חסם מלעיל <math>m\notin A</math> מתקיים כי <math>0\leq m</math>. | |||
***לכן לכל <math>x\in -A</math> מתקיים כי <math>x<-m<0</math> | |||
***כלומר כל האיברים ב<math>-A</math> שליליים, ולכן <math>-A\subseteq 0_D</math> כלומר <math>-A\leq 0_D</math> | |||
**בכיוון ההפוך, נניח כי <math>-A\leq 0_D</math> | |||
***לכן כל האיברים ב<math>-A</math> שליליים. | |||
***אם קיים <math>0>m\notin A</math> אזי <math>0<-\frac{m}{2}\in -A</math> בסתירה. | |||
**לכן כל המספרים השליליים שייכים לA, כלומר <math>0_D\subseteq A</math> ולכן <math>A\geq 0_D</math> | |||
==כפל חתכי דדקינד== | |||
*יהיו שני חתכי דדקינד '''אי שליליים''' <math>0_D\leq A,B</math>, נגדיר את הכפל: | |||
**<math>A\cdot B =\left\{x\cdot y|x\in A\setminus 0_D \wedge y\in B\setminus 0_D\right\}\cup 0_D</math> | |||
*אם A שלילי, וB אי שלילי, נגדיר: | |||
**<math>A\cdot B = - ((-A)\cdot B)</math> | |||
*אם A אי שלילי, וB שלילי, נגדיר: | |||
**<math>A\cdot B = - (A\cdot (-B))</math> | |||
*אם A,B שליליים נגדיר: | |||
**<math>A\cdot B = (-A)\cdot (-B)</math> | |||
===הוכחה שהמכפלה נותנת חתך דדקינד=== | |||
*יהיו שני חתכי דדקינד חיוביים <math>0_D< A,B</math> | |||
*ברור שהמכפלה לא ריקה כיוון ש <math>0_D\subseteq A\cdot B</math> | |||
*כיוון שA,B חתכי דדקינד מדובר בקבוצות חסומות, אז קיימים חסמי מלעיל <math>m_A,m_B</math> בהתאמה. | |||
*לכל <math>xy\in AB</math> מתקיים כי <math>x<m_A,y<m_B</math> ולכן <math>xy<m_A\cdot m_B</math>. זה נכון כי החסמים חיוביים, כי מדובר בחתכים חיוביים. | |||
*אם <math>t\in AB</math> צ"ל כי <math>t</math> אינו חסם מלעיל של <math>AB</math>. | |||
*אם <math>t\leq 0</math> ברור שאינו חסם מלעיל של <math>AB</math> כיוון שיש בקבוצה מספרים חיוביים. | |||
*לכן <math>t=xy\in AB</math>. | |||
*כיוון ש<math>x</math> אינו חסם מלעיל של <math>A</math> קיים <math>x<z\in A</math> ולכן <math>xy<zy\in A</math> בסתירה. | |||
*אם <math>t\not\in AB</math> צ"ל כי <math>t</math> חסם מלעיל. | |||
*נב"ש כי <math>t</math> אינו חסם מלעיל, לכן יש בקבוצה איבר גדול ממנו. | |||
*כיוון ש <math>t\not\in AB</math> נובע כי <math>t>0</math>, ולכן האיבר שגדול ממנו הוא מהצורה <math>t<xy</math>. | |||
*לכן <math>\frac{t}{y}<x</math>, נבחר <math>x_1 =\frac{t}{y}<x</math>. | |||
*כיוון ש<math>x_1 <x</math> נובע כי <math>x_1 \in A</math>. | |||
*לכן <math>t=x_1 y\in A\cdot B</math> בסתירה. | |||
*אם אחד החתכים הוא <math>0_D</math> קל להוכיח כי מכפלתם היא <math>0_D</math> ולכן מהווה חתך. | |||
===חתך היחידה=== | |||
*נגדיר את חתך היחידה, בהמשך נוכיח שהוא נייטרלי לכפל. | |||
*<math>1_D=\{x\in\mathbb{Q}|x<1\}</math> | |||
===הופכי=== | |||
*אם A חיובי נגדיר את ההופכי שלו להיות | |||
*<math>A^{-1}=\{x\in\mathbb{Q}|\exists m\not\in A:x<\frac{1}{m}\}</math> | |||
*אם A שלילי נגדיר את ההופכי שלו להיות | |||
*<math>A^{-1}=-(-A)^{-1}</math> | |||
====הוכחה שההופכי הוא חתך דדקינד==== | |||
*נניח A חיובי, ויהי <math>0<a\in A</math>. | |||
*לכל חסם <math>m\not\in A</math> מתקיים כי <math>a<m</math> | |||
*לפיכך <math>\frac{1}{m}<\frac{1}{a}</math> | |||
*לכן <math>\frac{1}{a}</math> הוא חסם מלעיל של <math>A^{-1}</math> | |||
*ברור כי <math>A^{-1}</math> אינו ריק, כי לA יש חסם מלעיל, וכל מספר שקטן ממהופכי שלו שייך ל<math>A^{-1}</math> | |||
*נוכיח כי כל מספר ב<math>A^{-1}</math> אינו חסם מלעיל. | |||
*אם <math>x<\frac{1}{m}\in A^{-1}</math> אז גם אמצע הקטע <math>x<y<\frac{1}{m}\in A^{-1}</math> | |||
*לבסוף, יהי <math>x</math> שאינו חסם מלעיל של <math>A^{-1}</math> | |||
*לכן <math>x<y\in A^{-1}</math> | |||
*והרי קיים חסם של A כך ש <math>y<\frac{1}{m}</math> | |||
*ולכן גם <math>x<\frac{1}{m}</math> ולכן <math>x\in A^{-1}</math> | |||
====הוכחה שאכן מדובר בהופכי==== | |||
*יהי A חיובי, נוכיח כי <math>A^{-1}A=1</math> | |||
*ראשית, נוכיח כי <math>A^{-1}A\leq 1</math> | |||
**יהי <math>0<xa\in A^{-1}A</math> | |||
**<math>x\in A^{-1}</math>, לכן קיים חסם מלעיל <math>m\not\in A</math> כך ש <math>x<\frac{1}{m}</math> | |||
**כמובן ש <math>a<m</math> | |||
**ביחד <math>xa<\frac{1}{m}\cdot m=1</math>. | |||
*כעת נוכיח כי <math>A^{-1}A\geq 1</math> | |||
*צ"ל כי אפשר לבחור איבר <math>xa\in A^{-1}A</math> הקרוב ל1 כרצוננו. | |||
*נבחר <math>0<a\in A, m\not\in A</math> כך ש <math>a,m</math> קרובים כרצוננו (אפשרי כי מכל זוג של מספר וחסם אפשר להחליף אחד מהם באמצע הקטע). | |||
*נבחר <math>x<\frac{1}{m}</math> כך ש<math>x,\frac{1}{m}</math> קרובים כרצוננו. | |||
*סה"כ <math>1-xa=m\cdot \frac{1}{m}-a\cdot \frac{1}{m}+a\cdot \frac{1}{m}-ax=\frac{1}{m}(m-a)+a(\frac{1}{m}-x)</math> | |||
*כיוון שקבוצת החסמים <math>m</math> חסומה מלמטה ע"י איברי חיובי מA, וכיוון שאפשר לקרב את <math>m-a</math> כרצוננו לאפס, סה"כ אפשר לקרב את ההפרש הזה כרצוננו לאפס, כפי שרצינו. | |||
*לבסוף, אם <math>A</math> שלילי, <math>A^{-1}=-(-A)^{-1}</math> | |||
*לכן <math>A^{-1}A=-(-A)^{-1}\cdot A = (-A)^{-1}\cdot (-A)=1</math> | |||
**המעבר האחרון הוא לפי הגדרת הכפל עבור חתכים שליליים. | |||
=שדה הממשיים= | |||
==הגדרת המספרים הממשיים== | |||
*הגדרה: <math>\mathbb{R}</math> הוא קבוצת כל חתכי דדקינד. | |||
==שדה הממשיים הוא סדר סדור== | |||
*נוכיח שמדובר ב[https://he.wikipedia.org/wiki/%D7%A9%D7%93%D7%94_%D7%A1%D7%93%D7%95%D7%A8 שדה סדור] ביחס לפעולות החיבור והכפל ויחס הסדר שהגדרנו לעיל. | |||
===הוכחה=== | |||
====תכונות השדה==== | |||
*סגירות - הוכחנו לעיל שסכום חתכים הוא חתך, וכן כפל חתכים הוא חתך | |||
*חילופיות - טריוויאלי מחילופיות החיבור והכפל ברציונאליים. | |||
*אסוציאטיביות - טריוויאלי מאסוציאטיביות החיבור והכפל ברציונאליים. | |||
*נייטרלים - הגדרנו איברים נייטרלים לעיל ואפילו הוכחנו שהם אכן נייטרלים | |||
*נגדיים - הגדרנו והוכחנו לעיל | |||
*הופכיים - הגדרנו והוכחנו לעיל | |||
*פילוג - נובע מפילוג הרציונאליים | |||
====תכונות שדה סדור==== | |||
*איזוטוניות ביחס לסכום: | |||
**יהיו חתכים A,B,C כך ש<math>A\leq B</math> צ"ל כי <math>A+C\leq B+C</math> | |||
**נתון כי <math>A\subseteq B</math> צ"ל כי <math>A+C\subseteq B+C</math> | |||
**יהי <math>a+c\in A+C</math>, לכן <math>a\in B</math> ולכן <math>a+c\in B+C</math>. | |||
*יהיו זוג חתכים <math>A\leq B</math> ויהי חתך <math>C</math> חיובי. צ"ל כי <math>AC\leq BC</math> | |||
**ראשית נניח כי A,B חתכים חיוביים | |||
***יהי <math>0<ac\in AC</math> כאשר <math>0<a,c</math>. | |||
***כיוון ש <math>A\subseteq B</math> נובע כי <math>a\in B</math> ולכן <math>ac\in BC</math>. | |||
**כעת נניח כי A שלילי ואילו B חיובי (המצב ההפוך סותר את הנתונים) | |||
***לפי הגדרת הכפל <math>AC=-((-A)C)</math> הוא חתך שלילי, ולכן בוודאי קטן מהחתך החיובי <math>BC</math> | |||
*לבסוף נניח כי A,B חתכים שליליים | |||
*ראשית נוכיח טענת עזר: <math>A\leq B</math> אם ורק אם <math>-A\geq -B</math> | |||
** בכיוון אחד, נתון כי <math>A\leq B</math> ורוצים להוכיח כי <math>-A\geq -B</math> | |||
***יהי <math>x\in -B</math>, כלומר קיים חסם <math>m\not\in B</math> כך ש <math>x<m</math> | |||
***כיוון ש<math>A\leq B</math> נובע כי <math>m\not\in A</math> ולכן <math>x\in -A</math> | |||
**בכיוון השני, נשתמש בכיוון הראשון ובעובדה כי <math>-(-A)=A</math> | |||
*כעת נחזור להוכחה: | |||
*מהנתון נובע כי <math>-A\geq -B</math> | |||
*כבר הוכחנו עבור חתכים חיוביים כי נובע ש <math>(-A)C\geq (-B)C</math> | |||
*לכן <math>-((-A)C)\leq -((-B)C)</math> | |||
*כלומר הוכחנו <math>AC\leq BC</math> | |||
==שלמות הממשיים== | |||
*תהי <math>\emptyset\neq A\subseteq \mathbb{R}</math> קבוצה לא ריקה של מספרים ממשיים, וחסומה מלעיל (כלומר קיים <math>M\in\mathbb{R}</math> כך ש<math>\forall a\in A:a\leq M</math>. אזי קיים ל<math>A</math> חסם עליון ממשי. | |||
===הוכחה=== | |||
* נסמן ב<math>S</math> את האיחוד הכללי של כל חתכי הדדקינד ששייכים ל<math>A</math>, כלומר <math>S=\cup_{x\in A} x</math> | |||
*נוכיח כי האיחוד הכללי של כל חתכי הדדקינד הוא גם חתך דדקינד. | |||
**<math>S</math> אינה ריקה | |||
***<math>A</math> אינה ריקה, ולכן קיים <math>x\in A</math>. | |||
***כיוון ש<math>x</math> חתך דדקינד הוא אינו ריק. | |||
***<math>x\subseteq S</math> ולכן <math>S</math> אינה ריקה | |||
**<math>S</math> חסומה: | |||
***כיוון ש<math>M</math> חסם מלעיל של <math>A</math> לכל <math>x\in A</math> מתקיים כי <math>x\leq M</math> | |||
***לפי יחס הסדר מתקיים כי <math>x\subseteq M</math>. | |||
***כיוון שלכל <math>x\in A</math> מתקיים כי <math>x\subseteq M</math> נובע כי גם <math>S\subseteq M</math>. | |||
***לכן <math>S</math> חסומה מלעיל. | |||
**נוכיח כי <math>x\in S</math> אם ורק אם <math>x</math> אינו חסם מלעיל של <math>S</math> | |||
***אם <math>x\in S</math> אזי <math>x\in D\in A</math> | |||
***אם <math>x</math> חסם מלעיל של <math>S</math> אזי הוא בפרט חסם מלעיל של <math>D</math> בסתירה. | |||
***מצד שני, אם <math>m</math> חסם מלעיל של <math>S</math> הוא בפרט חסם מלעיל של כל איברי <math>A</math> ולכן אינו שייך לאף אחד מאיברי <math>A</math> ולכן אינו שייך ל<math>S</math> | |||
*ברור כי לכל <math>x\in A</math> מתקיים כי <math>x\leq S</math> כיוון ש<math>x\subseteq S</math> (כל קבוצה מוכלת באיחוד). | |||
*נוכיח כי <math>S</math> הוא החסם העליון של <math>A</math>. | |||
*נב"ש כי קיים <math>T</math> חסם מלעיל של <math>A</math> כך ש <math>T<S</math>. | |||
*לכן קיים <math>x\in S\setminus T</math>. | |||
*לכן קיים <math>D\in A</math> כך ש <math>x\in D</math>. | |||
*לכן <math>D\not\subseteq T</math> בסתירה לכך ש<math>T</math> חסם מלעיל של <math>A</math> | |||
==ייצוג עשרוני של מספרים ממשיים== | |||
*ייצוג עשרוני הוא זוג של סדרת הספרות (פונקציה מהטבעיים אל קבוצת הספרות 0-9) ומספר טבעי שהוא מיקום של הספרה העשרונית. | |||
*נרצה להתאים לכל ייצוג עשרוני מספר ממשי, נגדיר אותו להיות החסם העליון של כל תתי הפיתוחים העשרוניים הסופיים של המספר. | |||
**אם <math>a_n</math> היא סדרת הספרות ו<math>k</math> הוא מיקום הנקודה העשרונית נגדיר את המספר להיות: | |||
**<math>\sup \{10^k \sum_{i=1}^n \frac{a_i}{10^i}|n\in\mathbb{N} \}</math> | |||
*דוגמא פשוטה: | |||
*עבור הסדרה הקבועה <math>a_n =9</math>, ומיקום הנקודה העשרונית <math>k=0</math> נקבל את הייצוג העשרוני <math>0.999...</math> | |||
*לפי ההגדרה לעיל יוצא כי: | |||
**<math>0.999...=\sup \{0,0.9,0.99,0.999,...\}</math> | |||
*קל להוכיח כי החסם העליון של קבוצה זו הוא 1. | |||
*1 הוא חסם מלעיל של הקבוצה | |||
*לכל מספר קטן מ1 יש איבר בקבוצה שגדול ממנו, כי סדרת איברי הקבוצה שואפת ל1. | |||
*מסקנה: <math>1=0.999...</math> | |||
גרסה אחרונה מ־07:58, 15 באוקטובר 2023
הקדמה
- אנחנו מעוניינים שבמערכת המספרים שלנו יהיה פתרון למשוואה [math]\displaystyle{ x^2=2 }[/math] (שורש שתיים).
- הרי אחרת, מה המרחק מהנקודה [math]\displaystyle{ (1,1) }[/math] לראשית הצירים [math]\displaystyle{ (0,0) }[/math]?
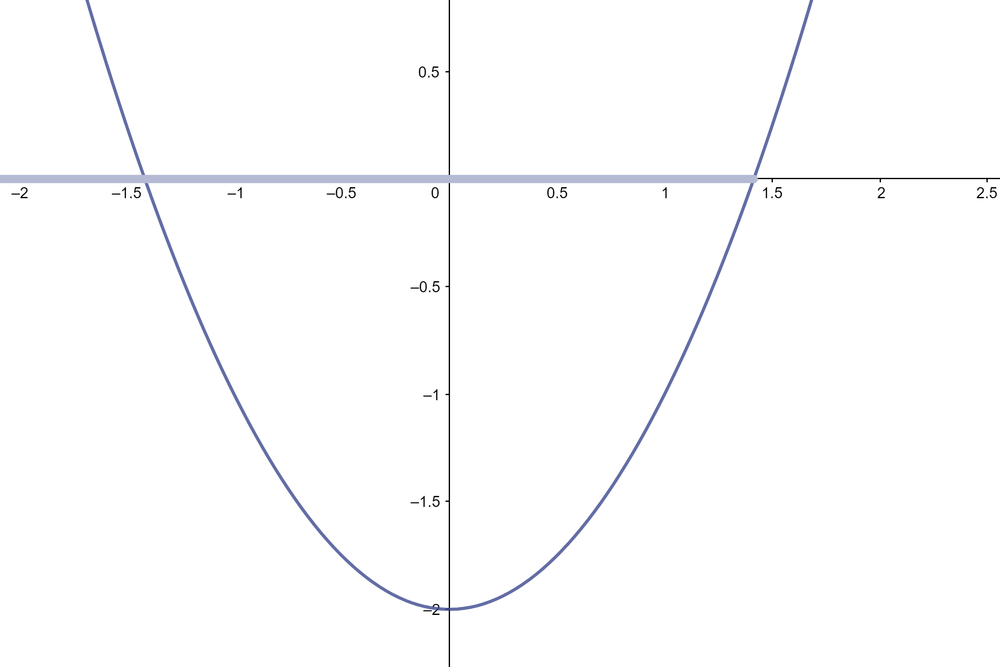
- האם ייתכן שהפרבולה [math]\displaystyle{ y=x^2-2 }[/math] עולה מהנקודה [math]\displaystyle{ (0,-2) }[/math] אל הנקודה [math]\displaystyle{ (2,2) }[/math] בלי לחתוך את ציר האיקס?
- כיוון שאין פתרון למשוואה זו בשדה הרציונאליים, אנחנו רוצים לבנות את שדה הממשיים.
- כיצד ניתן לתאר את נקודת החיתוך החיובית של הפרבולה [math]\displaystyle{ y=x^2-2 }[/math] עם ציר האיקס באמצעות המספרים הרציונאליים אם כך?
(נבנה באמצעות גאוגברה.)
- ובכן, ניתן לומר שציר המספרים מתחלק לשניים - לפני שורש שתיים ואחרי שורש שתיים.
- כלומר, אולי אנחנו יכולים לייצג את נקודת החיתוך על ידי אוסף הנקודות שקטנות ממנה [math]\displaystyle{ \left\{x\in\mathbb{Q}| x\lt 0 \vee x^2 \lt 2\right\} }[/math], זו הקרן באיור.
- הרעיון הזה של חיתוך ציר הרציונאליים סביב נקודה בלתי קיימת הוליד את חתכי דדקינד.
חתכי דדקינד
- הגדרה: חתך דדקינד הוא קבוצה [math]\displaystyle{ A\subseteq\mathbb{Q} }[/math] המקיימת:
- [math]\displaystyle{ A\neq\emptyset }[/math]
- [math]\displaystyle{ A }[/math] חסומה מלעיל.
- לכל [math]\displaystyle{ m\in\mathbb{Q} }[/math] מתקיים כי [math]\displaystyle{ m\notin A }[/math] אם ורק אם [math]\displaystyle{ m }[/math] חסם מלעיל של [math]\displaystyle{ A }[/math]
- הערות ותזכורות:
- חסם מלעיל של קבוצה הוא מספר שגדול יותר מכל איברי הקבוצה.
- בחתך דדקינד אין מספר גדול ביותר, אחרת זה היה חסם מלעיל ששיך לקבוצה. זה משול לחצי האבוקדו ללא הגרעין.
- בחתך המייצג מספר שאינו רציונאלי, כמו שורש שתיים, גם במשלים של החתך אין מספר קטן ביותר, זה משול לשני חצאי אבוקדו ללא גרעין כלל.
- אם מספר שייך לחתך, בוודאי כל מספר נמוך ממנו שייך לחתך הרי לא ייתכן שמספר נמוך ממנו הוא חסם מלעיל.
- הקרן באיור לעיל היא חתך דדקינד שתפקידו להגדיר את שורש שתיים.
- כיצד ניתן להתייחס לקבוצות כאלה בתור מספרים?
- עלינו להגיד פעולות בין חתכי דדקינד ולהוכיח שמדובר בשדה.
- כאשר נגדיר את הפעולות, נזכור שמטרתינו היא להגדיר את הנקודות "החסרות" על הציר.
חיבור חתכי דדקינד
- יהיו שתי חתכים [math]\displaystyle{ A,B }[/math], נגדיר את החיבור:
- [math]\displaystyle{ A+B=\left\{a+b|a\in A,b\in B\right\} }[/math]
- החיבור הוא חתך דדקינד בעצמו:
- כיוון שA,B אינן ריקות גם A+B אינה ריקה.
- סכום חסמי מלעיל של A וB חוסם את A+B.
- יהי [math]\displaystyle{ a+b\in A+B }[/math], כיוון שאיברי החתכים אינם חסמי מלעיל, קיימים [math]\displaystyle{ a\lt c\in A }[/math] וכן [math]\displaystyle{ b\lt d\in B }[/math] ולכן [math]\displaystyle{ a+b\lt c+d\in A+B }[/math] ו[math]\displaystyle{ a+b }[/math] אינו חסם מלעיל של [math]\displaystyle{ A+B }[/math]
- יהי [math]\displaystyle{ m\in\mathbb{Q} }[/math] שאינו חסם מלעיל של [math]\displaystyle{ A+B }[/math], לכן קיימים [math]\displaystyle{ m\lt a+b\in A+B }[/math]. כעת [math]\displaystyle{ m-a\lt b }[/math] כלומר [math]\displaystyle{ m-a }[/math] אינו חסם מלעיל של B ולכן שייך לקבוצה. סה"כ [math]\displaystyle{ m=a+(m-a)\in A+B }[/math].
חתך האפס
- נגדיר את חתך האפס:
- [math]\displaystyle{ 0_D=\left\{x\in\mathbb{Q}|x\lt 0\right\} }[/math]
- נוכיח כי חתך האפס נייטרלי לחיבור:
- יהי חתך דדקינד [math]\displaystyle{ A }[/math] צריך להוכיח כי [math]\displaystyle{ A+0_D=A }[/math]
- נבצע הכלה דו כיוונית. בכיוון הראשון:
- יהי [math]\displaystyle{ x=a+h\in A+0_D }[/math] צריך להוכיח כי [math]\displaystyle{ x\in A }[/math]
- כיוון ש [math]\displaystyle{ h\in 0_D }[/math] נובע לפי ההגדרה כי [math]\displaystyle{ h\lt 0 }[/math] ולכן [math]\displaystyle{ a+h\lt a }[/math]
- לכן [math]\displaystyle{ x=a+h }[/math] אינו חסם מלעיל של [math]\displaystyle{ A }[/math] ולכן [math]\displaystyle{ x\in A }[/math]
- בכיוון השני:
- יהי [math]\displaystyle{ a\in A }[/math] צריך להוכיח כי [math]\displaystyle{ a\in A+0_D }[/math]
- אמרנו כי בחתך דדקינד אין איבר גדול ביותר, ולכן קיים [math]\displaystyle{ a\lt b\in A }[/math]
- כיוון ש [math]\displaystyle{ a-b\lt 0 }[/math] נובע כי [math]\displaystyle{ a-b\in 0_D }[/math]
- סה"כ [math]\displaystyle{ a=b+(a-b)\in A+0_D }[/math] כפי שרצינו.
נגדי
- יהי חתך A, נגדיר את הנגדי:
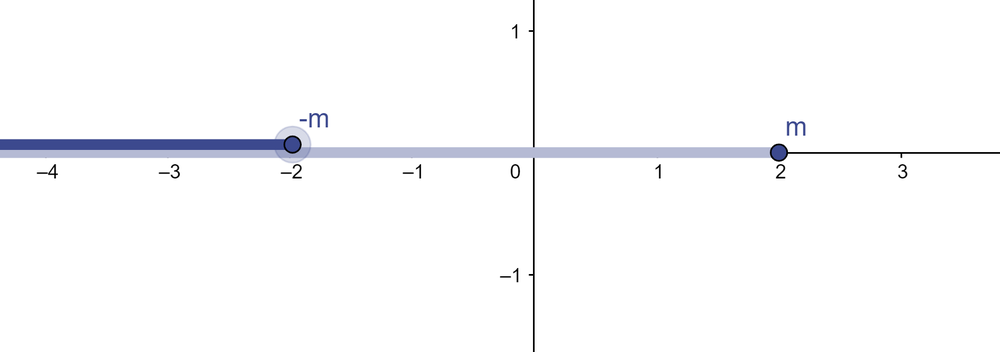
- [math]\displaystyle{ -A=\left\{x\in\mathbb{Q}|\exists m\notin A:x\lt -m\right\} }[/math]
- לדוגמא [math]\displaystyle{ -\left\{x\in\mathbb{Q}|x\lt 2\right\}=\left\{x\in\mathbb{Q}|x\lt -2\right\} }[/math]
- הנגדי הוא חתך דדקינד בעצמו:
- הנגדי לא ריק:
- כיוון שA חסומה מלעיל יש לה חסם, וכל המספרים שקטנים ממינוס החסם שייכים לנגדי, ולכן [math]\displaystyle{ -A\neq\emptyset }[/math]
- הנגדי חסום מלעיל:
- יהי [math]\displaystyle{ a\in A }[/math] לכן לכל [math]\displaystyle{ m\notin A }[/math] מתקיים כי [math]\displaystyle{ a\lt m }[/math] ולכן [math]\displaystyle{ -m\lt -a }[/math]
- לכל [math]\displaystyle{ x\in -A }[/math] קיים [math]\displaystyle{ m\notin A }[/math] כך ש [math]\displaystyle{ x\lt -m }[/math] ולכן [math]\displaystyle{ x\lt -a }[/math]
- בעצם הנגדי של כל איבר בA הוא חסם מלעיל של [math]\displaystyle{ -A }[/math].
- כל איבר בנגדי אינו חסם מלעיל:
- לכל איבר בנגדי [math]\displaystyle{ x\lt -m }[/math] לכן אמצע הקטע בין [math]\displaystyle{ x,-m }[/math] גדול מ[math]\displaystyle{ x }[/math] וקטן מ[math]\displaystyle{ -m }[/math] ולכן שייך לנגדי [math]\displaystyle{ -A }[/math] ולכן [math]\displaystyle{ x }[/math] אינו חסם מלעיל.
- אם איבר אינו חסם מלעיל, הוא שייך לנגדי:
- נניח [math]\displaystyle{ y }[/math] אינו חסם מלעיל של [math]\displaystyle{ -A }[/math] לכן קיים [math]\displaystyle{ y\lt x\in -A }[/math] ולכן קיים [math]\displaystyle{ m\notin A }[/math] כך ש [math]\displaystyle{ y\lt x\lt -m }[/math] ולכן [math]\displaystyle{ y\in -A }[/math]
- הנגדי לא ריק:
הוכחה שאכן מדובר באיבר נגדי
- יהי חתך [math]\displaystyle{ A }[/math] צריך להוכיח כי [math]\displaystyle{ A+(-A)=0_D }[/math]
- נבצע הכלה דו כיוונית
- בכיוון ראשון:
- יהי [math]\displaystyle{ x+y\in (A+(-A)) }[/math].
- כיוון ש[math]\displaystyle{ y\in (-A) }[/math] קיים [math]\displaystyle{ m\not\in A }[/math] כך ש [math]\displaystyle{ y\lt -m }[/math]
- לכן [math]\displaystyle{ x+y\lt m+y\lt 0 }[/math]
- לכן [math]\displaystyle{ x+y\in 0_D }[/math]
- בכיוון שני:
- יהי [math]\displaystyle{ t\in 0_D }[/math] כלומר [math]\displaystyle{ t\lt 0 }[/math]
- רוצים למצוא [math]\displaystyle{ a\in A, b\in (-A) }[/math] כך ש [math]\displaystyle{ a+b=t }[/math]
- נבחר [math]\displaystyle{ m\not\in A }[/math] כך ש[math]\displaystyle{ m+\frac{t}{2}\in A }[/math]
- מדוע זה אפשרי? כי אם [math]\displaystyle{ m+\frac{t}{2}\not\in A }[/math] אז זה חסם, ואפשר להוסיף לו [math]\displaystyle{ \frac{t}{2} }[/math] שזה מספר שלילי. אחרי מספיק פעמים נהיה קטנים מאיבר בקבוצה
- כעת [math]\displaystyle{ -m+\frac{t}{2}\lt -m }[/math] ולכן [math]\displaystyle{ -m+\frac{t}{2}\in (-A) }[/math].
- סה"כ [math]\displaystyle{ t=(m+\frac{t}{2})+(-m+\frac{t}{2})\in A+(-A) }[/math]
יחס סדר
- יחס ההכלה הוא יחס סדר לינארי (מלא) על קבוצת חתכי דדקינד
- הוכחה:
- יהיו שני חתכים A,B.
- אם קיים [math]\displaystyle{ m\notin A }[/math] חסם מלעיל של A כך ש[math]\displaystyle{ m\in B }[/math] אזי כל איבר של A אינו חסם מלעיל של B ולכן שייך לB, כלומר [math]\displaystyle{ A\subseteq B }[/math]
- אחרת, לכל [math]\displaystyle{ m\notin A }[/math] מתקיים כי [math]\displaystyle{ m\notin B }[/math]. כלומר [math]\displaystyle{ \overline{A}\subseteq\overline{B} }[/math] ולכן [math]\displaystyle{ B\subseteq A }[/math]
- נגדיר את החתכים החיוביים להיות כל החתכים A כך ש[math]\displaystyle{ 0_D \lt A }[/math] ונגדיר את החתכים השליליים על ידי [math]\displaystyle{ 0_D \gt A }[/math]
- טענה: [math]\displaystyle{ A\geq 0_D }[/math] אם ורק אם [math]\displaystyle{ -A\leq 0_D }[/math]
- הוכחה:
- ראשית נניח כי [math]\displaystyle{ A\geq 0_D }[/math]
- כלומר בעצם [math]\displaystyle{ 0_D\subseteq A }[/math] ולכן לכל חסם מלעיל [math]\displaystyle{ m\notin A }[/math] מתקיים כי [math]\displaystyle{ 0\leq m }[/math].
- לכן לכל [math]\displaystyle{ x\in -A }[/math] מתקיים כי [math]\displaystyle{ x\lt -m\lt 0 }[/math]
- כלומר כל האיברים ב[math]\displaystyle{ -A }[/math] שליליים, ולכן [math]\displaystyle{ -A\subseteq 0_D }[/math] כלומר [math]\displaystyle{ -A\leq 0_D }[/math]
- בכיוון ההפוך, נניח כי [math]\displaystyle{ -A\leq 0_D }[/math]
- לכן כל האיברים ב[math]\displaystyle{ -A }[/math] שליליים.
- אם קיים [math]\displaystyle{ 0\gt m\notin A }[/math] אזי [math]\displaystyle{ 0\lt -\frac{m}{2}\in -A }[/math] בסתירה.
- לכן כל המספרים השליליים שייכים לA, כלומר [math]\displaystyle{ 0_D\subseteq A }[/math] ולכן [math]\displaystyle{ A\geq 0_D }[/math]
- ראשית נניח כי [math]\displaystyle{ A\geq 0_D }[/math]
כפל חתכי דדקינד
- יהיו שני חתכי דדקינד אי שליליים [math]\displaystyle{ 0_D\leq A,B }[/math], נגדיר את הכפל:
- [math]\displaystyle{ A\cdot B =\left\{x\cdot y|x\in A\setminus 0_D \wedge y\in B\setminus 0_D\right\}\cup 0_D }[/math]
- אם A שלילי, וB אי שלילי, נגדיר:
- [math]\displaystyle{ A\cdot B = - ((-A)\cdot B) }[/math]
- אם A אי שלילי, וB שלילי, נגדיר:
- [math]\displaystyle{ A\cdot B = - (A\cdot (-B)) }[/math]
- אם A,B שליליים נגדיר:
- [math]\displaystyle{ A\cdot B = (-A)\cdot (-B) }[/math]
הוכחה שהמכפלה נותנת חתך דדקינד
- יהיו שני חתכי דדקינד חיוביים [math]\displaystyle{ 0_D\lt A,B }[/math]
- ברור שהמכפלה לא ריקה כיוון ש [math]\displaystyle{ 0_D\subseteq A\cdot B }[/math]
- כיוון שA,B חתכי דדקינד מדובר בקבוצות חסומות, אז קיימים חסמי מלעיל [math]\displaystyle{ m_A,m_B }[/math] בהתאמה.
- לכל [math]\displaystyle{ xy\in AB }[/math] מתקיים כי [math]\displaystyle{ x\lt m_A,y\lt m_B }[/math] ולכן [math]\displaystyle{ xy\lt m_A\cdot m_B }[/math]. זה נכון כי החסמים חיוביים, כי מדובר בחתכים חיוביים.
- אם [math]\displaystyle{ t\in AB }[/math] צ"ל כי [math]\displaystyle{ t }[/math] אינו חסם מלעיל של [math]\displaystyle{ AB }[/math].
- אם [math]\displaystyle{ t\leq 0 }[/math] ברור שאינו חסם מלעיל של [math]\displaystyle{ AB }[/math] כיוון שיש בקבוצה מספרים חיוביים.
- לכן [math]\displaystyle{ t=xy\in AB }[/math].
- כיוון ש[math]\displaystyle{ x }[/math] אינו חסם מלעיל של [math]\displaystyle{ A }[/math] קיים [math]\displaystyle{ x\lt z\in A }[/math] ולכן [math]\displaystyle{ xy\lt zy\in A }[/math] בסתירה.
- אם [math]\displaystyle{ t\not\in AB }[/math] צ"ל כי [math]\displaystyle{ t }[/math] חסם מלעיל.
- נב"ש כי [math]\displaystyle{ t }[/math] אינו חסם מלעיל, לכן יש בקבוצה איבר גדול ממנו.
- כיוון ש [math]\displaystyle{ t\not\in AB }[/math] נובע כי [math]\displaystyle{ t\gt 0 }[/math], ולכן האיבר שגדול ממנו הוא מהצורה [math]\displaystyle{ t\lt xy }[/math].
- לכן [math]\displaystyle{ \frac{t}{y}\lt x }[/math], נבחר [math]\displaystyle{ x_1 =\frac{t}{y}\lt x }[/math].
- כיוון ש[math]\displaystyle{ x_1 \lt x }[/math] נובע כי [math]\displaystyle{ x_1 \in A }[/math].
- לכן [math]\displaystyle{ t=x_1 y\in A\cdot B }[/math] בסתירה.
- אם אחד החתכים הוא [math]\displaystyle{ 0_D }[/math] קל להוכיח כי מכפלתם היא [math]\displaystyle{ 0_D }[/math] ולכן מהווה חתך.
חתך היחידה
- נגדיר את חתך היחידה, בהמשך נוכיח שהוא נייטרלי לכפל.
- [math]\displaystyle{ 1_D=\{x\in\mathbb{Q}|x\lt 1\} }[/math]
הופכי
- אם A חיובי נגדיר את ההופכי שלו להיות
- [math]\displaystyle{ A^{-1}=\{x\in\mathbb{Q}|\exists m\not\in A:x\lt \frac{1}{m}\} }[/math]
- אם A שלילי נגדיר את ההופכי שלו להיות
- [math]\displaystyle{ A^{-1}=-(-A)^{-1} }[/math]
הוכחה שההופכי הוא חתך דדקינד
- נניח A חיובי, ויהי [math]\displaystyle{ 0\lt a\in A }[/math].
- לכל חסם [math]\displaystyle{ m\not\in A }[/math] מתקיים כי [math]\displaystyle{ a\lt m }[/math]
- לפיכך [math]\displaystyle{ \frac{1}{m}\lt \frac{1}{a} }[/math]
- לכן [math]\displaystyle{ \frac{1}{a} }[/math] הוא חסם מלעיל של [math]\displaystyle{ A^{-1} }[/math]
- ברור כי [math]\displaystyle{ A^{-1} }[/math] אינו ריק, כי לA יש חסם מלעיל, וכל מספר שקטן ממהופכי שלו שייך ל[math]\displaystyle{ A^{-1} }[/math]
- נוכיח כי כל מספר ב[math]\displaystyle{ A^{-1} }[/math] אינו חסם מלעיל.
- אם [math]\displaystyle{ x\lt \frac{1}{m}\in A^{-1} }[/math] אז גם אמצע הקטע [math]\displaystyle{ x\lt y\lt \frac{1}{m}\in A^{-1} }[/math]
- לבסוף, יהי [math]\displaystyle{ x }[/math] שאינו חסם מלעיל של [math]\displaystyle{ A^{-1} }[/math]
- לכן [math]\displaystyle{ x\lt y\in A^{-1} }[/math]
- והרי קיים חסם של A כך ש [math]\displaystyle{ y\lt \frac{1}{m} }[/math]
- ולכן גם [math]\displaystyle{ x\lt \frac{1}{m} }[/math] ולכן [math]\displaystyle{ x\in A^{-1} }[/math]
הוכחה שאכן מדובר בהופכי
- יהי A חיובי, נוכיח כי [math]\displaystyle{ A^{-1}A=1 }[/math]
- ראשית, נוכיח כי [math]\displaystyle{ A^{-1}A\leq 1 }[/math]
- יהי [math]\displaystyle{ 0\lt xa\in A^{-1}A }[/math]
- [math]\displaystyle{ x\in A^{-1} }[/math], לכן קיים חסם מלעיל [math]\displaystyle{ m\not\in A }[/math] כך ש [math]\displaystyle{ x\lt \frac{1}{m} }[/math]
- כמובן ש [math]\displaystyle{ a\lt m }[/math]
- ביחד [math]\displaystyle{ xa\lt \frac{1}{m}\cdot m=1 }[/math].
- כעת נוכיח כי [math]\displaystyle{ A^{-1}A\geq 1 }[/math]
- צ"ל כי אפשר לבחור איבר [math]\displaystyle{ xa\in A^{-1}A }[/math] הקרוב ל1 כרצוננו.
- נבחר [math]\displaystyle{ 0\lt a\in A, m\not\in A }[/math] כך ש [math]\displaystyle{ a,m }[/math] קרובים כרצוננו (אפשרי כי מכל זוג של מספר וחסם אפשר להחליף אחד מהם באמצע הקטע).
- נבחר [math]\displaystyle{ x\lt \frac{1}{m} }[/math] כך ש[math]\displaystyle{ x,\frac{1}{m} }[/math] קרובים כרצוננו.
- סה"כ [math]\displaystyle{ 1-xa=m\cdot \frac{1}{m}-a\cdot \frac{1}{m}+a\cdot \frac{1}{m}-ax=\frac{1}{m}(m-a)+a(\frac{1}{m}-x) }[/math]
- כיוון שקבוצת החסמים [math]\displaystyle{ m }[/math] חסומה מלמטה ע"י איברי חיובי מA, וכיוון שאפשר לקרב את [math]\displaystyle{ m-a }[/math] כרצוננו לאפס, סה"כ אפשר לקרב את ההפרש הזה כרצוננו לאפס, כפי שרצינו.
- לבסוף, אם [math]\displaystyle{ A }[/math] שלילי, [math]\displaystyle{ A^{-1}=-(-A)^{-1} }[/math]
- לכן [math]\displaystyle{ A^{-1}A=-(-A)^{-1}\cdot A = (-A)^{-1}\cdot (-A)=1 }[/math]
- המעבר האחרון הוא לפי הגדרת הכפל עבור חתכים שליליים.
שדה הממשיים
הגדרת המספרים הממשיים
- הגדרה: [math]\displaystyle{ \mathbb{R} }[/math] הוא קבוצת כל חתכי דדקינד.
שדה הממשיים הוא סדר סדור
- נוכיח שמדובר בשדה סדור ביחס לפעולות החיבור והכפל ויחס הסדר שהגדרנו לעיל.
הוכחה
תכונות השדה
- סגירות - הוכחנו לעיל שסכום חתכים הוא חתך, וכן כפל חתכים הוא חתך
- חילופיות - טריוויאלי מחילופיות החיבור והכפל ברציונאליים.
- אסוציאטיביות - טריוויאלי מאסוציאטיביות החיבור והכפל ברציונאליים.
- נייטרלים - הגדרנו איברים נייטרלים לעיל ואפילו הוכחנו שהם אכן נייטרלים
- נגדיים - הגדרנו והוכחנו לעיל
- הופכיים - הגדרנו והוכחנו לעיל
- פילוג - נובע מפילוג הרציונאליים
תכונות שדה סדור
- איזוטוניות ביחס לסכום:
- יהיו חתכים A,B,C כך ש[math]\displaystyle{ A\leq B }[/math] צ"ל כי [math]\displaystyle{ A+C\leq B+C }[/math]
- נתון כי [math]\displaystyle{ A\subseteq B }[/math] צ"ל כי [math]\displaystyle{ A+C\subseteq B+C }[/math]
- יהי [math]\displaystyle{ a+c\in A+C }[/math], לכן [math]\displaystyle{ a\in B }[/math] ולכן [math]\displaystyle{ a+c\in B+C }[/math].
- יהיו זוג חתכים [math]\displaystyle{ A\leq B }[/math] ויהי חתך [math]\displaystyle{ C }[/math] חיובי. צ"ל כי [math]\displaystyle{ AC\leq BC }[/math]
- ראשית נניח כי A,B חתכים חיוביים
- יהי [math]\displaystyle{ 0\lt ac\in AC }[/math] כאשר [math]\displaystyle{ 0\lt a,c }[/math].
- כיוון ש [math]\displaystyle{ A\subseteq B }[/math] נובע כי [math]\displaystyle{ a\in B }[/math] ולכן [math]\displaystyle{ ac\in BC }[/math].
- כעת נניח כי A שלילי ואילו B חיובי (המצב ההפוך סותר את הנתונים)
- לפי הגדרת הכפל [math]\displaystyle{ AC=-((-A)C) }[/math] הוא חתך שלילי, ולכן בוודאי קטן מהחתך החיובי [math]\displaystyle{ BC }[/math]
- ראשית נניח כי A,B חתכים חיוביים
- לבסוף נניח כי A,B חתכים שליליים
- ראשית נוכיח טענת עזר: [math]\displaystyle{ A\leq B }[/math] אם ורק אם [math]\displaystyle{ -A\geq -B }[/math]
- בכיוון אחד, נתון כי [math]\displaystyle{ A\leq B }[/math] ורוצים להוכיח כי [math]\displaystyle{ -A\geq -B }[/math]
- יהי [math]\displaystyle{ x\in -B }[/math], כלומר קיים חסם [math]\displaystyle{ m\not\in B }[/math] כך ש [math]\displaystyle{ x\lt m }[/math]
- כיוון ש[math]\displaystyle{ A\leq B }[/math] נובע כי [math]\displaystyle{ m\not\in A }[/math] ולכן [math]\displaystyle{ x\in -A }[/math]
- בכיוון השני, נשתמש בכיוון הראשון ובעובדה כי [math]\displaystyle{ -(-A)=A }[/math]
- בכיוון אחד, נתון כי [math]\displaystyle{ A\leq B }[/math] ורוצים להוכיח כי [math]\displaystyle{ -A\geq -B }[/math]
- כעת נחזור להוכחה:
- מהנתון נובע כי [math]\displaystyle{ -A\geq -B }[/math]
- כבר הוכחנו עבור חתכים חיוביים כי נובע ש [math]\displaystyle{ (-A)C\geq (-B)C }[/math]
- לכן [math]\displaystyle{ -((-A)C)\leq -((-B)C) }[/math]
- כלומר הוכחנו [math]\displaystyle{ AC\leq BC }[/math]
שלמות הממשיים
- תהי [math]\displaystyle{ \emptyset\neq A\subseteq \mathbb{R} }[/math] קבוצה לא ריקה של מספרים ממשיים, וחסומה מלעיל (כלומר קיים [math]\displaystyle{ M\in\mathbb{R} }[/math] כך ש[math]\displaystyle{ \forall a\in A:a\leq M }[/math]. אזי קיים ל[math]\displaystyle{ A }[/math] חסם עליון ממשי.
הוכחה
- נסמן ב[math]\displaystyle{ S }[/math] את האיחוד הכללי של כל חתכי הדדקינד ששייכים ל[math]\displaystyle{ A }[/math], כלומר [math]\displaystyle{ S=\cup_{x\in A} x }[/math]
- נוכיח כי האיחוד הכללי של כל חתכי הדדקינד הוא גם חתך דדקינד.
- [math]\displaystyle{ S }[/math] אינה ריקה
- [math]\displaystyle{ A }[/math] אינה ריקה, ולכן קיים [math]\displaystyle{ x\in A }[/math].
- כיוון ש[math]\displaystyle{ x }[/math] חתך דדקינד הוא אינו ריק.
- [math]\displaystyle{ x\subseteq S }[/math] ולכן [math]\displaystyle{ S }[/math] אינה ריקה
- [math]\displaystyle{ S }[/math] חסומה:
- כיוון ש[math]\displaystyle{ M }[/math] חסם מלעיל של [math]\displaystyle{ A }[/math] לכל [math]\displaystyle{ x\in A }[/math] מתקיים כי [math]\displaystyle{ x\leq M }[/math]
- לפי יחס הסדר מתקיים כי [math]\displaystyle{ x\subseteq M }[/math].
- כיוון שלכל [math]\displaystyle{ x\in A }[/math] מתקיים כי [math]\displaystyle{ x\subseteq M }[/math] נובע כי גם [math]\displaystyle{ S\subseteq M }[/math].
- לכן [math]\displaystyle{ S }[/math] חסומה מלעיל.
- נוכיח כי [math]\displaystyle{ x\in S }[/math] אם ורק אם [math]\displaystyle{ x }[/math] אינו חסם מלעיל של [math]\displaystyle{ S }[/math]
- אם [math]\displaystyle{ x\in S }[/math] אזי [math]\displaystyle{ x\in D\in A }[/math]
- אם [math]\displaystyle{ x }[/math] חסם מלעיל של [math]\displaystyle{ S }[/math] אזי הוא בפרט חסם מלעיל של [math]\displaystyle{ D }[/math] בסתירה.
- מצד שני, אם [math]\displaystyle{ m }[/math] חסם מלעיל של [math]\displaystyle{ S }[/math] הוא בפרט חסם מלעיל של כל איברי [math]\displaystyle{ A }[/math] ולכן אינו שייך לאף אחד מאיברי [math]\displaystyle{ A }[/math] ולכן אינו שייך ל[math]\displaystyle{ S }[/math]
- [math]\displaystyle{ S }[/math] אינה ריקה
- ברור כי לכל [math]\displaystyle{ x\in A }[/math] מתקיים כי [math]\displaystyle{ x\leq S }[/math] כיוון ש[math]\displaystyle{ x\subseteq S }[/math] (כל קבוצה מוכלת באיחוד).
- נוכיח כי [math]\displaystyle{ S }[/math] הוא החסם העליון של [math]\displaystyle{ A }[/math].
- נב"ש כי קיים [math]\displaystyle{ T }[/math] חסם מלעיל של [math]\displaystyle{ A }[/math] כך ש [math]\displaystyle{ T\lt S }[/math].
- לכן קיים [math]\displaystyle{ x\in S\setminus T }[/math].
- לכן קיים [math]\displaystyle{ D\in A }[/math] כך ש [math]\displaystyle{ x\in D }[/math].
- לכן [math]\displaystyle{ D\not\subseteq T }[/math] בסתירה לכך ש[math]\displaystyle{ T }[/math] חסם מלעיל של [math]\displaystyle{ A }[/math]
ייצוג עשרוני של מספרים ממשיים
- ייצוג עשרוני הוא זוג של סדרת הספרות (פונקציה מהטבעיים אל קבוצת הספרות 0-9) ומספר טבעי שהוא מיקום של הספרה העשרונית.
- נרצה להתאים לכל ייצוג עשרוני מספר ממשי, נגדיר אותו להיות החסם העליון של כל תתי הפיתוחים העשרוניים הסופיים של המספר.
- אם [math]\displaystyle{ a_n }[/math] היא סדרת הספרות ו[math]\displaystyle{ k }[/math] הוא מיקום הנקודה העשרונית נגדיר את המספר להיות:
- [math]\displaystyle{ \sup \{10^k \sum_{i=1}^n \frac{a_i}{10^i}|n\in\mathbb{N} \} }[/math]
- דוגמא פשוטה:
- עבור הסדרה הקבועה [math]\displaystyle{ a_n =9 }[/math], ומיקום הנקודה העשרונית [math]\displaystyle{ k=0 }[/math] נקבל את הייצוג העשרוני [math]\displaystyle{ 0.999... }[/math]
- לפי ההגדרה לעיל יוצא כי:
- [math]\displaystyle{ 0.999...=\sup \{0,0.9,0.99,0.999,...\} }[/math]
- קל להוכיח כי החסם העליון של קבוצה זו הוא 1.
- 1 הוא חסם מלעיל של הקבוצה
- לכל מספר קטן מ1 יש איבר בקבוצה שגדול ממנו, כי סדרת איברי הקבוצה שואפת ל1.
- מסקנה: [math]\displaystyle{ 1=0.999... }[/math]