אנליזת פורייה - ארז שיינר: הבדלים בין גרסאות בדף
| שורה 702: | שורה 702: | ||
==הרצאה 6 - משוואת החום על טבעת, התמרת פורייה== | ==הרצאה 6 - משוואת החום על טבעת, התמרת פורייה== | ||
=== | ===משוואת החום על טבעת=== | ||
*נביט במד"ח החום על מוט עבור הפונקציה <math>u(x,t)</math>: | *נביט במד"ח החום על מוט עבור הפונקציה <math>u(x,t)</math>: | ||
**<math>u_t-ku_{xx}=0</math> | **<math>u_t-ku_{xx}=0</math> | ||
גרסה מ־09:45, 23 במאי 2019
מבחנים לדוגמא
תקציר ההרצאות
- ההרצאות מבוססות בחלקן על הספר המצויין 'טורי פוריה' של זעפרני ופינקוס.
הרצאה 1 - הקדמה ומקדמי פוריה
הקדמה - גלים
- מבלי להגדיר גל במפורש, גל הוא תופעה מחזורית.
- לגל שהוא פונקציה במשתנה אחד של ציר הזמן יש שלוש תכונות:
- תדר או אורך גל (אחד חלקי המחזור או המחזור)
- אמפליטודה (מרחק בין המקסימום למינימום)
- פאזה (מהי נק' ההתחלה של המחזור).
- אנחנו נתרכז כמעט באופן בלעדי בפונקציות הטריגונומטריות סינוס וקוסינוס, ונקרא להם גלים טריגונומטריים.
- מדוע דווקא סינוס וקוסינוס?
- למדנו במד"ר על המשוואה [math]\displaystyle{ y''=-k^2y }[/math] המתארת תנועה על מסה המחוברת לקפיץ
- זו למעשה תנועה כללית של גל - ככל שהוא מתרחק, גדל הכוח שמושך אותו למרכז. מיתר גיטרה הוא דוגמא טובה נוספת.
- הפתרון הכללי למד"ר הוא [math]\displaystyle{ y=a\sin(kt)+b\cos(kt) }[/math].
- הקבוע [math]\displaystyle{ k }[/math] קובע את התדר של כל גל.
- הקבועים [math]\displaystyle{ a,b }[/math] קובעים את האמפליטודה של כל גל.
- מה לגבי הפאזה?
- בפונקציה [math]\displaystyle{ a\sin(kt+t_0) }[/math], הקבוע [math]\displaystyle{ t_0 }[/math] קובע את הפאזה.
- ניתן להציג כל גל כזה באמצעות סינוס וקוסינוס ללא פאזה:
- [math]\displaystyle{ a\sin(kt+t_0)=(a\sin(t_0))cos(kt)+(a\cos(t_0))sin(kt) }[/math]
- האם גם ההפך נכון? כלומר האם כל צירוף לינארי [math]\displaystyle{ a\sin(kt)+b\cos(kt) }[/math] ניתן להציג כגל יחיד?
- תשובה: כן.
- הוכחה:
- נסמן [math]\displaystyle{ z=a+bi=rcis(\theta) }[/math]
- כלומר [math]\displaystyle{ a\sin(kt)+b\cos(kt)=r\sin(\theta)sin(kt)+r\cos(\theta)cos(kt)=rcos(kt-\theta) }[/math]
- שימו לב:
- סכמנו שני גלים מאותו תדר עם פאזה אפס, וקיבלנו גל חדש.
- הגל החדש הוא מאותו תדר כמו שני הגלים.
- לגל החדש יש פאזה שאינה אפס.
- האפליטודה של הגל החדש היא [math]\displaystyle{ r=\sqrt{a^2+b^2} }[/math].
- האם כל פונקציה היא סכום של גלים?
- בהנתן פונקציה שהיא סכום של גלים, כיצד נמצא מיהם הגלים המרכיבים אותה?
- האם יש דרך יחידה להרכיב פונקציה מגלים? (למעשה כבר ראינו שלא באופן כללי - הרי הצלחנו להציג גל אחד כסכום של שני גלים אחרים).
- למה בכלל מעניין אותנו לפרק פונקציה לגלים?
- במהלך ההרצאות נענה (לפחות חלקית) על השאלות הללו.
טורי פורייה ומקדמי פוריה
- טור פורייה הוא טור מהצורה [math]\displaystyle{ f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty \left[a_n\cos(nx)+b_n\sin(nx)\right] }[/math]
- אם פונקציה שווה לטור פורייה שלה, מהם המקדמים [math]\displaystyle{ a_n,b_n }[/math]?
חישובים להקדמה
- ראשית נזכור את הנוסחאות הטריגונומטריות:
- [math]\displaystyle{ \sin(a)\sin(b)=\frac{1}{2}\left[\cos(a-b)-\cos(a+b)\right] }[/math]
- [math]\displaystyle{ \cos(a)\cos(b)=\frac{1}{2}\left[\cos(a+b)+\cos(a-b)\right] }[/math]
- כעת, לכל [math]\displaystyle{ 0\neq n\in\mathbb{N} }[/math] נקבל:
- [math]\displaystyle{ \frac{1}{\pi}\int_{-\pi}^{\pi}\sin(nx)\sin(nx)dx = \frac{1}{2\pi}\int_{-\pi}^{\pi}(1-\cos(2nx))dx = \frac{1}{2\pi}\left[x-\frac{1}{2n}\sin(2nx)\right]_{-\pi}^{\pi}=1 }[/math]
- עבור [math]\displaystyle{ n\neq k \in \mathbb{N} }[/math] נקבל:
- [math]\displaystyle{ \int_{-\pi}^{\pi}\sin(nx)\sin(kx)dx = \frac{1}{2}\int_{-\pi}^{\pi}(\cos((n-k)x)-\cos((n+k)x))dx = \frac{1}{2}\left[\frac{\sin((n-k)x)}{n-k}-\frac{\sin((n+k)x)}{n+k}\right]_{-\pi}^{\pi}=0 }[/math]
- שימו לב כי השתמשנו כאן בעובדה ש[math]\displaystyle{ n-k,n+k\neq 0 }[/math].
- באופן דומה, לכל [math]\displaystyle{ 0\neq n\in\mathbb{N} }[/math] נקבל:
- [math]\displaystyle{ \frac{1}{\pi}\int_{-\pi}^{\pi}\cos(nx)\cos(nx)dx = \frac{1}{2\pi}\int_{-\pi}^{\pi}(\cos(2nx)+1)dx = \frac{1}{2\pi}\left[\frac{1}{2n}\sin(2nx)+x\right]_{-\pi}^{\pi}=1 }[/math]
- עבור [math]\displaystyle{ n\neq k \in \mathbb{N} }[/math] נקבל:
- [math]\displaystyle{ \int_{-\pi}^{\pi}\cos(nx)\cos(kx)dx = \frac{1}{2}\int_{-\pi}^{\pi}(\cos((n+k)x)+\cos((n-k)x))dx = \frac{1}{2}\left[\frac{\sin((n+k)x)}{n+k}+\frac{\sin((n-k)x)}{n-k}\right]_{-\pi}^{\pi}=0 }[/math]
- שימו לב כי השתמשנו כאן בעובדה ש[math]\displaystyle{ n-k,n+k\neq 0 }[/math].
- עבור [math]\displaystyle{ n,k\in \mathbb{N} }[/math] נקבל:
- [math]\displaystyle{ \int_{-\pi}^{\pi}\cos(nx)\sin(kx)dx=0 }[/math] כיוון שמדובר באינטגרל בקטע סימטרי על פונקציה אי זוגית.
- ולבסוף, עבור [math]\displaystyle{ n=0 }[/math] נקבל
- [math]\displaystyle{ \frac{1}{\pi}\int_{-\pi}^{\pi}\cos(0)\cos(0)dx=\frac{1}{\pi}\int_{-\pi}^{\pi}1dx=2 }[/math]
- שימו לב שכאשר מציבים 0 בsin מקבלים אפס, ולכן אין צורך בבדיקה הזו.
- הערה חשובה:
- למעשה כלל החישובים שעשינו לעיל מוכיחים שהקבוצה [math]\displaystyle{ \{\frac{1}{\sqrt{2}},sin(x),cos(x),sin(2x),cos(2x),...\} }[/math] מהווה קבוצה אורתונורמלית לפי המכפלה הפנימית [math]\displaystyle{ \langle f,g\rangle=\frac{1}{\pi}\int_{-\pi}^{\pi}(f\cdot g) dx }[/math]
מקדמי הטור
- כעת תהי פונקציה ששווה לטור פורייה, ועוד נניח שהטור מתכנס במ"ש.
- [math]\displaystyle{ \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(kx)dx = \frac{1}{\pi}\int_{-\pi}^{\pi}\left(\frac{a_0}{2}+\sum_{n=1}^\infty \left[a_n\cos(nx)+b_n\sin(nx)\right]\right)\cos(kx)dx= }[/math]
- [math]\displaystyle{ =\frac{1}{\pi}\int_{-\pi}^{\pi}\left(\frac{a_0}{2}\cos(kx)+\sum_{n=1}^\infty \left[a_n\cos(nx)\cos(kx)+b_n\sin(nx)\cos(kx)\right]\right)dx= }[/math]
- כיוון שהטור מתכנס במ"ש, מותר לנו לעשות אינטגרציה איבר איבר
- [math]\displaystyle{ =\frac{1}{\pi}\int_{-\pi}^{\pi}\frac{a_0}{2}\cos(kx)dx + \sum_{n=1}^\infty \left[\frac{1}{\pi}\int_{-\pi}^{\pi}\left(a_n\cos(nx)\cos(kx)+b_n\sin(nx)\cos(kx)\right)dx\right] }[/math]
- לפי חישובי האינטגרלים לעיל, כמעט הכל מתאפס וסה"כ נקבל:
- [math]\displaystyle{ a_k=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(kx)dx }[/math]
- שימו לב שחישוב זה נכון בפרט עבור [math]\displaystyle{ k=0 }[/math].
- באופן דומה נקבל כי [math]\displaystyle{ b_k=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin(kx)dx }[/math]
- הוכחנו שאם פונקציה שווה לטור פורייה, והטור מתכנס במ"ש, אזי הוא יחיד והמקדמים שלו נקבעים על ידי הנוסחאות לעיל.
- השאלה היא אילו פונקציות שוות לטור פורייה.
- באופן מיידי, ברור שטור פורייה הוא פונקציה עם מחזור [math]\displaystyle{ 2\pi }[/math].
- לכן בדר"כ אנו שואלים האם ההמשך המחזורי של הפונקציה שווה לטור פורייה:
- תהי פונקציה [math]\displaystyle{ f }[/math], נגדיר את ההמשך המחזורי שלה [math]\displaystyle{ g }[/math] על ידי:
- לכל [math]\displaystyle{ k\in\mathbb{Z} }[/math] ולכל [math]\displaystyle{ x\in [-\pi+2\pi k,\pi+2\pi k) }[/math] נגדיר [math]\displaystyle{ g(x)=f(x-2\pi k) }[/math].
- ברור ש [math]\displaystyle{ g(x+2\pi) = g(x) }[/math], כלומר קיבלנו פונקציה מחזורית.
- ניתן גם לרשום בנוסחא מקוצרת [math]\displaystyle{ g(x)=f(x-2\pi\lfloor\frac{x+\pi}{2\pi}\rfloor) }[/math]
- לדוגמא, ההמשך המחזורי של [math]\displaystyle{ x^2 }[/math]:
דוגמא
- נחשב את מקדמי הפורייה של ההמשך המחזורי של [math]\displaystyle{ x^2 }[/math]
- שימו לב, מקדמי הפורייה של פונקציה וההמשך המחזורי שלה זהים, כיוון שערך הפונקציה בנקודה אחת לא משפיע על האינטגרל.
- [math]\displaystyle{ b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}x^2\sin(nx)dx=0 }[/math].
- שימו לב: מקדמי הפורייה של הסינוסים תמיד יתאפסו עבור פונקציה זוגית, ומקדמי הפורייה של הקוסינוסים תמיד יתאפסו עבור פונקציה אי זוגית.
- [math]\displaystyle{ a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}x^2dx =\frac{2}{\pi}\int_{0}^{\pi}x^2dx= \frac{2}{\pi}\left[\frac{1}{3}x^3\right]_{0}^{\pi} = \frac{2\pi^2}{3} }[/math]
- [math]\displaystyle{ a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}x^2\cos(nx)dx=\frac{2}{\pi}\int_{0}^{\pi}x^2\cos(nx)dx =\left\{\begin{array}{lr}f'=\cos(nx) & g=x^2\\ f= \frac{\sin(nx)}{n} & g'=2x\end{array}\right\}= }[/math]
- [math]\displaystyle{ =\frac{2}{\pi}\left[\frac{x^2\sin(nx)}{n}\right]_0^{\pi} - \frac{4}{n\pi}\int_{0}^{\pi}x\sin(nx)dx = - \frac{4}{n\pi}\int_{0}^{\pi}x\sin(nx)dx= \left\{\begin{array}{lr}f'=\sin(nx) & g=x\\ f= -\frac{\cos(nx)}{n} & g'=1\end{array}\right\}= }[/math]
- [math]\displaystyle{ - \frac{4}{n\pi}\left[\frac{-x\cos(nx)}{n}\right]_0^\pi + \frac{4}{n^2\pi}\int_0^\pi \cos(nx)dx=\frac{4\pi\cos(\pi n)}{n^2\pi}+\frac{4}{n^3\pi}\left[sin(nx)\right]_0^\pi = \frac{4(-1)^n}{n^2} }[/math]
- שימו לב כי לכל [math]\displaystyle{ n\in\mathbb{N} }[/math] מתקיים כי [math]\displaystyle{ cos(n\pi)=(-1)^n }[/math]
- סה"כ אם ההמשך המחזורי של [math]\displaystyle{ x^2 }[/math] שווה לטור פורייה שמתכנס במ"ש, אזי טור זה הוא:
- [math]\displaystyle{ \frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4(-1)^n}{n^2}cos(nx) }[/math]
- נניח (ונוכיח בהמשך) שטור זה אכן שווה לפונקציה ונציב [math]\displaystyle{ \pi }[/math].
- [math]\displaystyle{ \pi^2 = \frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4}{n^2} }[/math]
- ונקבל את הסכום המפורסם
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{1}{n^2}=\frac{\pi^2}{6} }[/math]
הרצאה 2 - למת רימן לבג, גרעין דיריכלה
מרחבי מכפלה פנימית שאינם ממימד סופי והיטלים
- פונקציה נקראת רציפה למקוטעין בקטע סופי אם:
- 1. היא רציפה פרט אולי למספר סופי של נקודות.
- 2. הגבולות החד צדדיים הרלוונטיים בכל נקודה הם סופיים.
- למעשה נקודות אי הרציפות היחידות של פונקציה רציפה למקוטעין הן ממין ראשון (קפיצתיות).
- פונקציה נקראת רציפה למקוטעין בקטע כללי, אם ניתן לחלק אותו לקטעים סופיים בהן הפונקציה רציפה למקוטעין.
- E הוא המרחב הוקטורי של כל הפונקציות הרציפות למקוטעין [math]\displaystyle{ f:[-\pi,\pi]\to\mathbb{C} }[/math] מעל השדה [math]\displaystyle{ \mathbb{C} }[/math], המקיימות בנוסף שבכל נקודה ערך הפונקציה שווה לממוצע בין הגבולות החד צדדיים שלה, ובקצוות ערך הנקודה שווה לגבול החד צדדי המוגדר.
- לא קשה להוכיח שאכן מדובר במרחב וקטורי. בעיקר יש לשים לב לכך שסכום פונקציות בקבוצה נשאר בקבוצה.
- [math]\displaystyle{ \langle f,g\rangle=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\overline{g(x)}dx }[/math] היא מכפלה פנימית מעל E.
- [math]\displaystyle{ \langle g,f\rangle = \frac{1}{\pi}\int_{-\pi}^{\pi}g(x)\overline{f(x)}dx = \overline{\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\overline{g(x)}dx} = \overline{\langle f,g\rangle} }[/math]
- [math]\displaystyle{ \langle af+bg,h\rangle = a\langle f,h\rangle + b\langle g,h\rangle }[/math]
- [math]\displaystyle{ \langle f,f\rangle = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\overline{f(x)}dx = \frac{1}{\pi}\int_{-\pi}^{\pi}|f|^2dx }[/math]
- בכל קטע רציפות האינטגרל על פונקציה חיובית הוא אפס אם ורק אם היא אפס.
- כיוון שהפונקציה בכל נקודה שווה לאחד הגבולות החד צדדיים או לממוצע בניהם, נובע שאם האינטגרל לעיל מתאפס הפונקציה חייבת להתאפס לחלוטין.
- נביט בנורמה המושרית [math]\displaystyle{ ||f||^2=\langle f,f\rangle }[/math]
- כעת נוכיח מספר תכונות של היטלים במרחבי מכפלה פנימית.
- יש לנקוט בזהירות מיוחדת בנושא זה, כיוון שאנו עוסקים במרחבים שאינם נוצרים סופית (אין להם בסיס סופי או מימד).
- ייתכן שהוכחתם חלק מהמשפטים הבאים רק עבור מרחבים נוצרים סופית.
- תהי קבוצה אורתונורמלית סופית [math]\displaystyle{ \{e_1,...,e_n\} }[/math], ונקרא למרחב שהיא פורשת W.
- לכל וקטור [math]\displaystyle{ v\in V }[/math] נגדיר את ההיטל של [math]\displaystyle{ v }[/math] על W על ידי [math]\displaystyle{ \widetilde{v}=\sum_{i=1}^n\langle v,e_i\rangle e_i }[/math]
- נוכיח מספר תכונות לגבי ההיטל הזה:
- מתקיים כי [math]\displaystyle{ \langle v,\widetilde{v}\rangle = \langle \widetilde{v},\widetilde{v}\rangle=\sum_{i=1}^n |\langle v,e_i\rangle|^2 }[/math]
- הוכחה:
- [math]\displaystyle{ \langle v,\widetilde{v}\rangle = \langle v,\sum_{i=1}^n\langle v,e_i\rangle e_i\rangle = \sum_{i=1}^n \overline{\langle v,e_i\rangle}\langle v,e_i\rangle = \sum_{i=1}^n |\langle v,e_i\rangle|^2 }[/math]
- [math]\displaystyle{ \langle \widetilde{v},\widetilde{v}\rangle = \langle \sum_{i=1}^n\langle v,e_i\rangle e_i,\sum_{i=1}^n\langle v,e_i\rangle e_i\rangle = \sum_{i=1}^n |\langle v,e_i\rangle|^2 }[/math]
- המעבר האחרון נכון כיוון ש [math]\displaystyle{ \{e_1,...,e_n\} }[/math] אורתונורמלית.
- מתקיים כי [math]\displaystyle{ ||v||^2=||v-\widetilde{v}||^2+||\widetilde{v}||^2 }[/math]
- הוכחה:
- [math]\displaystyle{ \langle v-\widetilde{v},v-\widetilde{v}\rangle = \langle v,v\rangle - \langle v,\widetilde{v}\rangle - \langle \widetilde{v},v\rangle + \langle \widetilde{v},\widetilde{v}\rangle }[/math]
- נזכור כי [math]\displaystyle{ \langle v,\widetilde{v}\rangle = \langle \widetilde{v},\widetilde{v}\rangle }[/math].
- לכן קיבלנו כי [math]\displaystyle{ ||v-\widetilde{v}||^2 = ||v||^2 - ||\widetilde{v}||^2 }[/math]
- מסקנה מיידית: [math]\displaystyle{ ||\widetilde{v}||\leq ||v|| }[/math]
אי שיוויון בסל
- כעת תהי קבוצה אורתונורמלית אינסופית [math]\displaystyle{ \{e_1,e_2,...\} }[/math].
- לכל [math]\displaystyle{ v\in V }[/math] מתקיים כי [math]\displaystyle{ \sum_{i=1}^\infty |\langle v,e_i\rangle|^2 \leq ||v||^2 }[/math]
- הוכחה:
- ראינו שלכל n מתקיים כי [math]\displaystyle{ \sum_{i=1}^n |\langle v,e_i\rangle|^2 \leq ||v||^2 }[/math].
- כלומר סדרת הסכומים החלקיים של הטור החיובי חסומה על ידי [math]\displaystyle{ ||v||^2 }[/math] ולכן הטור מתכנס למספר שקטן או שווה לו.
- בפרט נובע כי
- [math]\displaystyle{ \lim_{n\to\infty}|\langle v,e_i\rangle|=0 }[/math]
למת רימן לבג
- ראינו כי [math]\displaystyle{ \{\sin(x),\cos(x),\sin(2x),\cos(2x),...\} }[/math] היא קבוצה אורתונורמלית ב[math]\displaystyle{ E }[/math] (כרגע אנו לא צריכים את הפונקציה הקבועה).
- כמו כן לכל פונקציה f הגדרנו מקדמי פורייה ע"י:
- לכל [math]\displaystyle{ 1\leq n\in \mathbb{N} }[/math] הגדרנו [math]\displaystyle{ a_n=\langle f,\cos(nx)\rangle }[/math], ו[math]\displaystyle{ b_n=\langle f,\sin(nx)\rangle }[/math]
- נובע מאי שיוויון בסל כי המקדמים שואפים לאפס.
- כלומר:
- [math]\displaystyle{ \lim_{n\to\infty}\frac{1}{\pi}\int_{-\pi}^\pi f(x)\cos(nx)dx = 0 }[/math]
- [math]\displaystyle{ \lim_{n\to\infty}\frac{1}{\pi}\int_{-\pi}^\pi f(x)\sin(nx)dx = 0 }[/math]
- למת רימן-לבג: תהי [math]\displaystyle{ g }[/math] רציפה למקוטעין בקטע [math]\displaystyle{ [0,\pi] }[/math], אזי:
- [math]\displaystyle{ \lim_{n\to\infty}\int_{0}^\pi g(t)\sin\left(\left(n+\frac{1}{2}\right)t\right)dt = 0 }[/math]
- הוכחה:
- [math]\displaystyle{ \int_{0}^\pi g(t)\sin\left(\left(n+\frac{1}{2}\right)t\right)dt = \int_{0}^\pi g(t)\cos(\frac{t}{2})\sin(nt) dt+\int_{0}^\pi g(t)\sin(\frac{t}{2})\cos(nt) dt }[/math]
- נגדיר את שתי הפונקציות [math]\displaystyle{ h_s(t)=\begin{cases}g(t)\sin(\frac{t}{2}) & 0\leq t\leq \pi \\ 0 & -\pi\leq t \lt 0\end{cases} }[/math] ו [math]\displaystyle{ h_c(t)=\begin{cases}g(t)\cos(\frac{t}{2}) & 0\leq t\leq \pi \\ 0 & -\pi\leq t \lt 0\end{cases} }[/math]
- קל לראות כי שתי הפונקציות רציפות למקוטעין. לכן פרט לשינוי במספר סופי של נקודות שלא משפיע על האינטגרל, ניתן להניח כי [math]\displaystyle{ h_c,h_s\in E }[/math].
- ביחד נקבל כי [math]\displaystyle{ \int_{0}^\pi g(t)\sin\left(\left(n+\frac{1}{2}\right)t\right)dt = \int_{-\pi}^\pi h_c(t)sin(nt)dt + \int_{-\pi}^\pi h_s(t)sin(nt)dt \to 0 }[/math]
גרעין דיריכלה
- גרעין דיריכלה הוא הפונקציה [math]\displaystyle{ D_n(t)= \frac{\sin\left(\left(n+\frac{1}{2}\right)t\right)}{2\sin(\frac{t}{2})} }[/math]
- טענה: [math]\displaystyle{ D_n(t)=\frac{1}{2}+\sum_{k=1}^n \cos(kt) }[/math] בכל נקודה [math]\displaystyle{ t\neq 2\pi k }[/math]
- הוכחה:
- נכפל ב[math]\displaystyle{ 2\sin(\frac{t}{2}) }[/math] ונקבל בצד שמאל:
- [math]\displaystyle{ \sin(\frac{t}{2}) + 2\sin(\frac{t}{2})\cos(t) + 2\sin(\frac{t}{2})\cos(2t)+...+2\sin(\frac{t}{2})\cos(nt) }[/math]
- נבחין בזהות הטריגונומטרית [math]\displaystyle{ 2\sin(a)\cos(b) = \sin(b+a)-\sin(b-a) }[/math]
- ובפרט [math]\displaystyle{ 2\sin(\frac{t}{2})\cos(kt) = \sin(kt+\frac{t}{2}) - \sin(kt-\frac{t}{2}) }[/math]
- ביחד נקבל [math]\displaystyle{ \sin(\frac{t}{2}) + \sin(t+\frac{t}{2})-\sin(t-\frac{t}{2}) + \sin(2t+\frac{t}{2}) - \sin(2t-\frac{t}{2})+...+\sin(nt+\frac{t}{2}) - \sin(nt-\frac{t}{2}) = \sin(nt+\frac{t}{2}) = \sin\left(\left(n+\frac{1}{2}\right)t\right) }[/math]
- נשים לב כי הפונקציה [math]\displaystyle{ 2\sin(\frac{t}{2}) }[/math] מתאפסת בנקודות [math]\displaystyle{ t=2\pi k }[/math], בנקודות אלו לגרעין דיריכלה יש אי רציפות סליקה.
- זה נכון כיוון שפרט לנקודות אלו מדובר בפונקציה רציפה.
- כמו כן, גרעין דיריכלה מחזורי [math]\displaystyle{ 2\pi }[/math] כיוון שהוא סכום של פונקציות מחזוריות [math]\displaystyle{ 2\pi }[/math].
- נחשב את האינטגרל על גרעין דיריכלה:
- ראשית, לכל [math]\displaystyle{ 1\leq k \in \mathbb{N} }[/math] מתקיים:
- [math]\displaystyle{ \int_0^\pi \cos(kt)dt = \left[\frac{\sin(kt)}{k}\right]_0^\pi = 0 }[/math]
- לכן נקבל:
- [math]\displaystyle{ \frac{1}{\pi}\int_0^\pi D_n(t)dt = \frac{1}{\pi}\int_0^\pi \left[\frac{1}{2} + \cos(t) + \cos(2t)+...+\cos(nt)\right]dt = \frac{1}{\pi}\int_0^\pi \frac{1}{2}dt = \frac{1}{2} }[/math]
הסכומים החלקיים של טור פוריה
- תהיה נקודה x, נביט בסדרת הסכומים החלקיים של טור הפוריה המתאים לפונקציה [math]\displaystyle{ f }[/math] שהיא מחזורית [math]\displaystyle{ 2\pi }[/math]:
- [math]\displaystyle{ S_n = \frac{a_0}{2} + \sum_{k=1}^n a_k\cos(kx)+b_k\sin(kx) }[/math]
- נציב את מקדמי פוריה ונקבל כי:
- [math]\displaystyle{ S_n = \frac{1}{\pi}\int_{-\pi}^\pi \frac{1}{2}f(t)dt + \sum_{k=1}^n \left[\frac{1}{\pi}\int_{-\pi}^\pi f(t)\cos(kt)dt\right]\cos(kx)+\left[\frac{1}{\pi}\int_{-\pi}^\pi f(t)\sin(kt)dt\right]\sin(kx)= }[/math]
- [math]\displaystyle{ = \frac{1}{\pi}\int_{-\pi}^\pi\left[\frac{1}{2}f(t)+\sum_{k=1}^n f(t)\left(\cos(kt)\cos(kx) + \sin(kt)\sin(kx)\right)\right]dt= }[/math]
- [math]\displaystyle{ =\frac{1}{\pi}\int_{-\pi}^\pi f(t)\left[\frac{1}{2}+\sum_{k=1}^n \cos(k(t-x))\right]dt }[/math]
- זה בעצם גרעין דיריכלה, כלומר קיבלנו כי:
- [math]\displaystyle{ S_n = \frac{1}{\pi}\int_{-\pi}^\pi f(t)D_n(t-x)dt }[/math]
- שימו לב ששינוי מספר סופי של נקודות לא משפיע על האינטגרל, ולכן נקודות אי הרציפות הסליקות של גרעין דיריכלה לא פוגעות בהוכחה.
- טענה: תהי [math]\displaystyle{ f }[/math] פונקציה מחזורית [math]\displaystyle{ 2\pi }[/math]. אזי לכל [math]\displaystyle{ a\in\mathbb{R} }[/math] מתקיים כי:
- [math]\displaystyle{ \int_{-\pi}^\pi f(x)dx = \int_{-\pi+a}^{\pi+a} f(x)dx }[/math]
- כלומר, השטח מתחת לגרף הפונקציה שווה על כל קטע באורך [math]\displaystyle{ 2\pi }[/math].
- הוכחה:
- [math]\displaystyle{ \int_{-\pi+a}^{\pi+a} f(x)dx = \int_{-\pi+a}^{\pi} f(x)dx + \int_{\pi}^{\pi+a} f(x)dx }[/math]
- נבצע הצבה [math]\displaystyle{ t=x-2\pi }[/math] באינטגרל השני ונקבל:
- [math]\displaystyle{ \int_{\pi}^{\pi+a} f(x)dx = \{t=x-2\pi, dt=dx\} = \int_{-\pi}^{-\pi+a}f(t+2\pi)dt = \int_{-\pi}^{-\pi+a}f(t)dt = \int_{-\pi}^{-\pi+a}f(x)dx }[/math]
- ביחד נקבל כי:
- [math]\displaystyle{ \int_{-\pi+a}^{\pi+a} f(x)dx=\int_{-\pi+a}^{\pi} f(x)dx + \int_{-\pi}^{-\pi+a}f(x)dx = \int_{-\pi}^\pi f(x)dx }[/math]
- נחזור לסכומים החלקיים ונבצע הצבה:
- [math]\displaystyle{ S_n = \frac{1}{\pi}\int_{-\pi}^\pi f(t)D_n(t-x)dt = \{ u=t-x, du=dt\} = \frac{1}{\pi}\int_{-\pi-x}^{\pi-x} f(x+u)D_n(u)du }[/math]
- כיוון שגרעין דיריכלה ו[math]\displaystyle{ f }[/math] הן מחזוריות, נקבל:
- [math]\displaystyle{ S_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x+u)D_n(u)du=\frac{1}{\pi}\int_{-\pi}^{\pi} f(x+t)D_n(t)dt }[/math]
הרצאה 3 התכנסות נקודתית של טורי פוריה
סימונים והגדרות
- נסמן את הגבול החד צדדי מימין ב[math]\displaystyle{ f(d^+)=\lim_{x\to d^+}f(x) }[/math].
- נסמן את הגבול החד צדדי משמאל ב[math]\displaystyle{ f(d^-)=\lim_{x\to d^-}f(x) }[/math].
- שימו לב: אם הפונקציה רציפה למקוטעין, הערכים הללו תמיד מוגדרים.
- נגדיר את הנגזרת הימנית ע"י [math]\displaystyle{ f'(x^+) = \lim_{t\to 0^+}\frac{f(x+t)-f(x^+)}{t} }[/math].
- נגדיר את הנגזרת השמאלית ע"י [math]\displaystyle{ f'(x^-) = \lim_{t\to 0^-}\frac{f(x+t)-f(x^-)}{t} }[/math].
- שימו לב: ייתכן ש[math]\displaystyle{ f'(d^+)=f'(d^-) }[/math] אך הפונקציה אינה גזירה בd. זה יקרה אם היא לא רציפה בנקודה.
דוגמא:
- נביט בפונקציה [math]\displaystyle{ f(x)=\frac{x}{|x|} }[/math]
- מתקיים כי [math]\displaystyle{ f(0^+)=1 }[/math], ו[math]\displaystyle{ f(0^-)=-1 }[/math].
- כמו כן מתקיים כי [math]\displaystyle{ f'(0^+)=f'(0^-)=0 }[/math].
כמובן שהפונקציה אינה רציפה ואינה גזירה ב0.
משפט דיריכלה - התכנסות נקודתית של טור פוריה
- תהי [math]\displaystyle{ f }[/math] פונקציה מחזורית [math]\displaystyle{ 2\pi }[/math], רציפה למקוטעין כך שבכל נקודה הנגזרות החד צדדיות שלה קיימות וסופיות.
- אזי לכל [math]\displaystyle{ x\in\mathbb{R} }[/math] הטור עם מקדמי הפוריה של [math]\displaystyle{ f }[/math] מתכנס:
- [math]\displaystyle{ \frac{f(x^+)+f(x^-)}{2}=\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx) + b_n\sin(nx) }[/math]
- בפרט, בכל נקודה בה הפונקציה רציפה טור הפוריה מתכנס נקודתית לפונקציה, ובכל נקודה בה יש אי רציפות קפיצתית טור הפוריה מתכנס לממוצע הגבולות מימין ומשמאל.
הוכחה
- תהי נקודה [math]\displaystyle{ x\in\mathbb{R} }[/math].
- נביט בפונקציה [math]\displaystyle{ g(t) = \frac{f(x+t) - f(x^+)}{2\sin(\frac{t}{2})} }[/math]
- [math]\displaystyle{ \lim_{t\to 0^+}g(t) = \lim_{t\to 0^+}\frac{f(x+t) - f(x^+)}{t}\frac{\frac{t}{2}}{\sin(\frac{t}{2})} = f'(x^+)\cdot 1 }[/math]
- כיוון שהנגזרות החד צדדיות קיימות וסופיות, קיבלנו ש[math]\displaystyle{ g(t) }[/math] רציפה למקוטעין בקטע [math]\displaystyle{ [0,\pi] }[/math].
- לפי למת רימן-לבג נובע כי:
- [math]\displaystyle{ \lim_{n\to\infty}\int_0^\pi g(t)\sin\left(\left(n+\frac{1}{2}\right)t\right)dt=0 }[/math]
- כלומר:
- [math]\displaystyle{ 0=\lim_{n\to\infty}\frac{1}{\pi}\int_0^\pi \left[f(x+t)-f(x^+)\right]\frac{\sin\left(\left(n+\frac{1}{2}\right)t\right)}{2\sin(\frac{t}{2})}dt= \lim_{n\to\infty}\frac{1}{\pi}\int_0^\pi \left[f(x+t)-f(x^+)\right]D_n(t)dt }[/math]
- כיוון ש
- [math]\displaystyle{ \frac{1}{\pi}\int_0^\pi f(x^+)D_n(t)dt = \frac{f(x^+)}{2} }[/math]
- נובע כי:
- [math]\displaystyle{ \lim_{n\to\infty}\frac{1}{\pi}\int_0^\pi f(x+t)D_n(t)dt = \frac{f(x^+)}{2} }[/math]
- באופן דומה לחלוטין ניתן להוכיח כי:
- [math]\displaystyle{ \lim_{n\to\infty}\frac{1}{\pi}\int_{-\pi}^0 f(x+t)D_n(t)dt = \frac{f(x^-)}{2} }[/math]
- ולכן סה"כ נקבל כי:
- [math]\displaystyle{ \lim_{n\to\infty} S_n(x)= \lim_{n\to\infty}\frac{1}{\pi}\int_{-\pi}^{\pi} f(x+t)D_n(t)dt = \frac{f(x^-)+f(x^+)}{2} }[/math]
דוגמאות
דוגמא 1
- תהי [math]\displaystyle{ f }[/math] ההמשך המחזורי של [math]\displaystyle{ x }[/math].
- כיוון שf רציפה למקוטעין ובעלת נגזרות חד צדדיות קיימות (כולן שוות 1), תנאי משפט דיריכלה מתקיימים.
- כיוון שf הינה אי-זוגית, לכל [math]\displaystyle{ n }[/math] מתקיים כי [math]\displaystyle{ a_n=0 }[/math].
- כעת נחשב את המקדמים של הסינוסים:
- [math]\displaystyle{ b_n=\langle f,sin(nx)\rangle = \frac{1}{\pi}\int_{\pi}^\pi x\sin(nx)dx =\frac{2}{\pi}\int_{0}^\pi x\sin(nx)dx= \frac{2}{n\pi}\left[-x\cos(nx)\right]_{0}^\pi + \frac{2}{n\pi}\int_{0}^{\pi}\cos(nx)dx = -\frac{2\pi\cos(\pi n)}{\pi n} = \frac{2(-1)^{n+1}}{n} }[/math]
- לכן, בכל נקודת רציפות של f, כלומר בכל נקודה [math]\displaystyle{ x\neq \pi +2\pi k }[/math], מתקיים כי:
- [math]\displaystyle{ f(x)=\sum_{n=1}^\infty\frac{2(-1)^{n+1}}{n}\sin(nx) }[/math].
- בפרט, לכל נקודה [math]\displaystyle{ x\in (-\pi,\pi) }[/math] מתקיים כי:
- [math]\displaystyle{ x=\sum_{n=1}^\infty\frac{2(-1)^{n+1}}{n}\sin(nx) }[/math]
- עבור נקודות אי הרציפות (הקפיצתיות), מתקיים כי הממוצע בין הגבולות החד צדדיים הוא אפס.
- קל לראות שאכן לכל [math]\displaystyle{ x=\pi+2\pi k }[/math] נקבל שטור הפורייה מתכנס לאפס (למעשה כל הסינוסים מתאפסים).
- נציב לדוגמא [math]\displaystyle{ x=\frac{\pi}{2} }[/math] ונקבל:
- [math]\displaystyle{ \frac{\pi}{2}=\sum_{n=1}^\infty\frac{2(-1)^{n+1}}{n}\sin(\frac{n\pi}{2}) }[/math]
- לכל n זוגי הסינוס יתאפס, ולכן נקבל:
- [math]\displaystyle{ \frac{\pi}{2}=\sum_{n=1}^\infty\frac{2}{2n-1}\sin(n\pi-\frac{\pi}{2}) =\sum_{n=1}^\infty\frac{-2}{2n-1}\cos(n\pi) = \sum_{n=1}^\infty\frac{2(-1)^{n+1}}{2n-1} }[/math]
- שימו לב שהפעם לא קיבלנו טור חדש בזכות פורייה, כיוון שנקבל בדיוק את אותו הטור אם נציב 1 בטור הטיילור של [math]\displaystyle{ arctan(x) }[/math].
דוגמא 2
- כעת, תהי [math]\displaystyle{ g }[/math] ההמשך המחזורי של [math]\displaystyle{ x^2 }[/math].
- הפונקציה g הינה רציפה בכל הממשיים.
- הפונקציה g גזירה בכל הממשיים פרט לנקודות [math]\displaystyle{ x=\pi+2\pi k }[/math].
- בנקודות אי הגזירות, הנגזרות החד צדדיות קיימות ושוות ל[math]\displaystyle{ \pm 2\pi }[/math] (כיוון שהנגזרת של [math]\displaystyle{ x^2 }[/math] היא [math]\displaystyle{ 2x }[/math]).
- סה"כ לפי משפט דיריכלה, טור הפוריה של g מתכנס אליה בכל הממשיים (כיוון שהיא רציפה בכל הממשיים).
- כלומר קיבלנו שלכל [math]\displaystyle{ x\in [-\pi,\pi] }[/math] מתקיים כי:
- [math]\displaystyle{ x^2=\frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4(-1)^n}{n^2}cos(nx) }[/math]
- שימו לב שאם נגזור איבר איבר את טור הפוריה של [math]\displaystyle{ x^2 }[/math], נקבל את טור הפורייה של [math]\displaystyle{ 2x }[/math].
- האם זה מפתיע?
דוגמא 3
- תהי [math]\displaystyle{ h }[/math] ההמשך המחזורי של הפונקציה [math]\displaystyle{ \begin{cases}x & x\in [0,\pi]\\0 & x\in [-\pi,0)\end{cases} }[/math]
- שוב, קיבלנו פונקציה רציפה למקוטעין עם נגזרות חד צדדיות קיימות וסופיות.
- נחשב את מקדמי הפורייה:
- [math]\displaystyle{ a_0=\frac{1}{\pi}\int_0^\pi xdx = \frac{\pi}{2} }[/math]
- [math]\displaystyle{ a_n = \frac{1}{\pi}\int_0^\pi x\cos(nx)dx = \frac{1}{n\pi}\left[x\sin(nx)\right]_0^\pi - \frac{1}{n\pi}\int_0^\pi \sin(nx)dx = \frac{1}{n^2\pi}\left[\cos(nx)\right]_0^\pi= \frac{(-1)^n-1}{\pi n^2} }[/math]
- [math]\displaystyle{ b_n = \frac{1}{\pi}\int_0^\pi x\sin(nx)dx = \frac{-1}{n\pi}\left[x\cos(nx)\right]_0^\pi + \frac{1}{n\pi}\int_0^\pi \cos(nx)dx = \frac{(-1)^{n+1}}{n} }[/math]
- סה"כ שלכל [math]\displaystyle{ x\in (-\pi,\pi) }[/math] מתקיים כי:
- [math]\displaystyle{ h(x) = \frac{\pi}{4} + \sum_{n=1}^\infty \left[\frac{(-1)^n-1}{\pi n^2}\cos(nx) + \frac{(-1)^{n+1}}{n}\sin(nx)\right] }[/math]
- שימו לב: מצאנו שני טורי פורייה שמתכנסים ל[math]\displaystyle{ x }[/math] בקטע [math]\displaystyle{ (0,\pi) }[/math].
- באופן דומה אפשר להראות שקיימים אינסוף טורי פורייה כאלה.
טור הנגזרת
- תהי [math]\displaystyle{ f }[/math] רציפה בקטע [math]\displaystyle{ [-\pi,\pi] }[/math] כך שהנגזרת שלה [math]\displaystyle{ f' }[/math] רציפה למקוטעין בקטע.
שימוש בנוסחאת ניוטון לייבניץ לחישוב האינטגרל המסויים
- שימו לב שמותר לנו להשתמש בנוסחאת ניוטון לייבניץ:
- כיוון שהנגזרת רציפה למקוטעין, אפשר להראות בעזרת לופיטל שהנגזרות החד צדדיות בנקודות אי הגזירות של f קיימות.
- בעצם, זה מראה שf גזירה בקטעים סגורים בהם אפשר להפעיל את נוסחאת ניוטון לייבניץ.
- אם נחשב את האינטגרל על הנגזרת בכל הקטעים הסגורים, ערכי f יצטמצמו, פרט לקצוות.
- לדוגמא:
- [math]\displaystyle{ \int_{-1}^1 \frac{x}{|x|}dx = \int_{-1}^0 (-1)dx + \int_{0}^1 (1)dx = (-x)|_{-1}^0+(x)|_0^1 = 0-1 + 1-0 = 1-1 }[/math]
- כלומר קיבלנו כי [math]\displaystyle{ \int_{-1}^1 \frac{x}{|x|}dx = (|x|)_{-1}^{1} }[/math], כאשר [math]\displaystyle{ (|x|)' = \frac{x}{|x|} }[/math]
חישוב מקדמי טור הפורייה של הנגזרת
- נסמן את מקדמי הפורייה של [math]\displaystyle{ f }[/math] ב[math]\displaystyle{ a_n,b_n }[/math]
- נחשב את מקדמי הפורייה של הנגזרת, נסמן אותם ב[math]\displaystyle{ \alpha_n,\beta_n }[/math]:
- [math]\displaystyle{ \alpha_0=\frac{1}{\pi}\int_{-\pi}^{\pi}f'(x)dx= \frac{f(\pi)-f(-\pi)}{\pi} }[/math]
- [math]\displaystyle{ \alpha_n=\frac{1}{\pi} \int_{-\pi}^\pi f'(x)\cos(nx)dx = \frac{1}{\pi}\left[f(x)\cos(nx)\right]_{-\pi}^\pi +\frac{n}{\pi}\int_{-\pi}^\pi f(x)\sin(nx)dx = \frac{(-1)^n\left(f(\pi)-f(-\pi)\right)}{\pi}+n\cdot b_n = (-1)^n\alpha_0+nb_n }[/math]
- [math]\displaystyle{ \beta_n=\frac{1}{\pi} \int_{-\pi}^\pi f'(x)\sin(nx)dx = \frac{1}{\pi}\left[f(x)\sin(nx)\right]_{-\pi}^\pi -\frac{n}{\pi}\int_{-\pi}^\pi f(x)\cos(nx)dx = -n\cdot a_n }[/math]
- כלומר, בתנאים הנתונים, אם טור הפוריה של f הינו:
- [math]\displaystyle{ f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx) }[/math]
- אזי טור הפורייה של הנגזרת הינו:
- [math]\displaystyle{ f'(x)=\frac{\alpha_0}{2}+\sum_{n=1}^\infty \left((-1)^n\alpha_0+nb_n\right)\cos(nx)-n\cdot a_n\sin(nx) }[/math]
- במקרה המיוחד בו [math]\displaystyle{ f(-\pi)=f(\pi) }[/math] מתקיים כי [math]\displaystyle{ \alpha_0=0 }[/math] ולכן נקבל את טור הפורייה הפשוט:
- [math]\displaystyle{ f'(x)=\sum_{n=1}^\infty nb_n\cos(nx)-na_n\sin(nx) }[/math]
דוגמאות
דוגמא 1
- נזכר בטור הפורייה של [math]\displaystyle{ x^2 }[/math]:
- [math]\displaystyle{ \frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4(-1)^n}{n^2}cos(nx) }[/math]
- נרצה למצוא את מקדמי הפוריה של [math]\displaystyle{ \frac{x^3}{3} }[/math], נסמנם ב[math]\displaystyle{ a_n,b_n }[/math].
- לכל [math]\displaystyle{ 1\leq n }[/math] נקבל כי:
- [math]\displaystyle{ \frac{2(-1)^n\pi^2}{3}+nb_n = \frac{4(-1)^n}{n^2} }[/math]
- [math]\displaystyle{ -na_n = 0 }[/math]
- כמו כן נחשב את המקדם הראשון:
- [math]\displaystyle{ a_0=\frac{1}{\pi}\int_{-\pi}^\pi \frac{x^3}{3}dx = 0 }[/math]
- נחלץ את המקדמים ונקבל כי טור הפורייה של [math]\displaystyle{ \frac{x^3}{3} }[/math] הוא:
- [math]\displaystyle{ \frac{x^3}{3} = \sum_{n=1}^\infty \frac{2(-1)^n}{n^3}\left(2-\frac{\pi^2 n^2}{3}\right)\sin(nx) }[/math]
דוגמא 2
- נחשב את טור הפורייה של [math]\displaystyle{ e^x }[/math].
- נסמן את טור הפורייה של [math]\displaystyle{ e^x }[/math] ב:
- [math]\displaystyle{ \frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx) }[/math]
- כמובן שהנגזרת במקרה הזה שווה לפונקציה, ולכן יש לה בדיוק אותו טור פורייה.
- מצד שני, טור הפורייה של הנגזרת צריך להיות:
- [math]\displaystyle{ \frac{\alpha_0}{2}+\sum_{n=1}^\infty \left((-1)^n\alpha_0+nb_n\right)\cos(nx) -na_n\sin(nx) }[/math]
- כאשר [math]\displaystyle{ \alpha_0=\frac{f(\pi)-f(-\pi)}{\pi}=\frac{e^\pi-e^{-\pi}}{\pi} }[/math]
- ביחד נקבל את המשוואות:
- [math]\displaystyle{ a_0=\alpha_0 }[/math]
- [math]\displaystyle{ a_n=(-1)^n\alpha_0+nb_n }[/math]
- [math]\displaystyle{ b_n=-na_n }[/math]
- נציב את המשוואה השלישית בשנייה ונקבל:
- [math]\displaystyle{ a_n=\frac{(-1)^n\alpha_0}{1+n^2} }[/math]
- ולכן
- [math]\displaystyle{ b_n=\frac{n(-1)^{n+1}\alpha_0}{1+n^2} }[/math]
- סה"כ קיבלנו כי טור הפורייה של [math]\displaystyle{ e^x }[/math] הינו:
- [math]\displaystyle{ \frac{\alpha_0}{2}+\sum_{n=1}^\infty \frac{(-1)^n\alpha_0}{1+n^2}\cos(nx) + \frac{n(-1)^{n+1}\alpha_0}{1+n^2}\sin(nx) }[/math]
- כיוון שלהמשך המחזורי של [math]\displaystyle{ e^x }[/math] יש אי רציפות קפיצתית ב[math]\displaystyle{ x=\pi }[/math], טור הפורייה שם מתכנס לממוצע [math]\displaystyle{ \frac{e^\pi+e^{-\pi}}{2} }[/math]
- כלומר, אם נציב [math]\displaystyle{ x=\pi }[/math] נקבל:
- [math]\displaystyle{ \frac{1}{\alpha_0}\frac{e^\pi+e^{-\pi}}{2} = \frac{1}{2} +\sum_{n=1}^\infty \frac{1}{1+n^2} }[/math]
- נפשט:
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{1}{1+n^2}=\frac{\pi(e^\pi+e^{-\pi})}{2(e^\pi-e^{-\pi})}-\frac{1}{2} }[/math]
הרצאה 4 - התכנסות במ"ש ושיוויון פרסבל
תנאי להתכנסות במ"ש של טור פורייה
- תהי [math]\displaystyle{ f }[/math] רציפה בקטע [math]\displaystyle{ [-\pi,\pi] }[/math] המקיימת [math]\displaystyle{ f(-\pi)=f(\pi) }[/math], כך ש [math]\displaystyle{ f' }[/math] רציפה למקוטעין.
- אזי טור הפורייה של [math]\displaystyle{ f }[/math] מתכנס אליה במ"ש בכל הממשיים.
- לפי משפט דיריכלה ידוע כי טור הפורייה של ההמשך המחזורי של f מתכנס אליה בכל נקודה.
- נסמן את טור הפורייה ב
- [math]\displaystyle{ \frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx) }[/math]
- ברור כי
- [math]\displaystyle{ \left|\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx)\right|\leq \frac{|a_0|}{2} + \sum_{n=1}^\infty |a_n|+|b_n| }[/math]
- לפי מבחן ה-M של ויירשטראס, מספיק להוכיח שטור המספרים מימין מתכנס על מנת להסיק שטור הפורייה מתכנס במ"ש.
- נסמן את מקדמי פורייה של הנגזרת ב[math]\displaystyle{ \alpha_n,\beta_n }[/math].
- כבר חישבנו ש:
- [math]\displaystyle{ \alpha_0=0 }[/math]
- [math]\displaystyle{ \alpha_n=nb_n }[/math]
- [math]\displaystyle{ \beta_n=-na_n }[/math]
- לכן ביחד נקבל כי [math]\displaystyle{ \sqrt{|a_n|^2+|b_n|^2}=\frac{1}{n}\sqrt{|\alpha_n|^2+|\beta_n|^2} }[/math]
- לפי אי שיוויון קושי שוורץ, נקבל כי לכל n מתקיים:
- [math]\displaystyle{ \sum_{n=1}^N \frac{\sqrt{|\alpha_n|^2+|\beta_n|^2}}{n} \leq \sqrt{\sum_{n=1}^N\frac{1}{n^2}}\sqrt{\sum_{n=1}^N |\alpha_n|^2+|\beta_n|^2} }[/math]
- לפי אי שיוויון בסל, אנו יודעים כי הטור [math]\displaystyle{ \sum_{n=1}^\infty |\alpha_n|^2+|\beta_n|^2 }[/math] מתכנס, כיוון שמדובר במקדמי פורייה של [math]\displaystyle{ f'\in E }[/math].
- (זכרו שמותר להניח כי [math]\displaystyle{ f'\in E }[/math] על ידי שינוי מספר סופי של נקודות שלא משפיעות על חישוב מקדמי הפורייה.)
- לכן [math]\displaystyle{ \left(\sum_{n=1}^N\frac{1}{n^2}\right),\left(\sum_{n=1}^N |\alpha_n|^2+|\beta_n|^2\right) }[/math] חסומות כסדרות סכומים חלקיים של טורים מתכנסים.
- לכן סה"כ [math]\displaystyle{ \sum_{n=1}^N \frac{\sqrt{|\alpha_n|^2+|\beta_n|^2}}{n} }[/math] חסומה, ולכן הטור האינסופי המתאים לה מתכנס.
- סה"כ קיבלנו כי [math]\displaystyle{ \sum_{n=1}^\infty \sqrt{|a_n|^2+|b_n|^2} }[/math] מתכנס.
- לכן בוודאי גם הטורים הקטנים יותר [math]\displaystyle{ \sum_{n=1}^\infty |a_n| }[/math] ו[math]\displaystyle{ \sum_{n=1}^\infty |b_n| }[/math] מתכנסים, כפי שרצינו.
שיוויון פרסבל
- נביט במערכת האורתונורמלית [math]\displaystyle{ \{\frac{1}{\sqrt{2}},\cos(x),\sin(x),\cos(2x),\sin(2x),...\}\subseteq E }[/math], ותהי [math]\displaystyle{ f\in E }[/math].
- ידוע לנו כי [math]\displaystyle{ a_0=\langle f,1\rangle }[/math], ולכן [math]\displaystyle{ \frac{a_0}{\sqrt{2}}=\langle f,\frac{1}{\sqrt{2}}\rangle }[/math]
- נסמן את סדרת הסכומים החלקיים של טור הפורייה המתאים לפונקציה f ב [math]\displaystyle{ S_n }[/math].
- [math]\displaystyle{ S_n }[/math] היא ההיטל של [math]\displaystyle{ f }[/math] על הקבוצה האורתונורמלית [math]\displaystyle{ \{\frac{1}{\sqrt{2}},\cos(x),\sin(x),\cos(2x),\sin(2x),...,\cos(nx),\sin(nx)\} }[/math]
- אכן [math]\displaystyle{ \langle f,\frac{1}{\sqrt{2}}\rangle \frac{1}{\sqrt{2}} + \sum_{n=1}^\infty \langle f,\cos(nx)\rangle \cos(nx) + \langle f,\sin(nx)\rangle \sin(nx) = \frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx) }[/math]
- נזכור כי [math]\displaystyle{ ||v||^2=||v-\widetilde{v}||^2+||\widetilde{v}||^2 }[/math]
- לכן [math]\displaystyle{ ||f-S_n||^2=||f||^2-||S_n||^2 }[/math].
- כמו כן, נזכור כי [math]\displaystyle{ ||\widetilde{v}||^2 = \sum_{i=1}^{n}|\langle v,e_i\rangle|^2 }[/math]
- לכן [math]\displaystyle{ ||S_n||^2 = \frac{|a_0|^2}{2}+\sum_{k=1}^n |a_k|^2+|b_k|^2 }[/math]
- אי שיוויון בסל אומר כי [math]\displaystyle{ \sum_{i=1}^\infty |\langle v,e_i\rangle|^2 \leq ||v||^2 }[/math]
- כלומר:
- [math]\displaystyle{ \frac{|a_0|^2}{2}+\sum_{n=1}^\infty |a_n|^2+|b_n|^2 \leq ||f||^2 = \langle f,f\rangle = \frac{1}{\pi}\int_{-\pi}^{\pi} |f(x)|^2dx }[/math]
- משפט שיוויון פרסבל אומר שבעצם מתקיים שיוויון:
- [math]\displaystyle{ \frac{1}{\pi}\int_{-\pi}^{\pi} |f(x)|^2dx=\frac{|a_0|^2}{2}+\sum_{n=1}^\infty |a_n|^2+|b_n|^2 }[/math]
- אם נוכיח ש [math]\displaystyle{ ||f-S_n||^2\to 0 }[/math], נסיק כי [math]\displaystyle{ ||S_n||^2\to ||f||^2 }[/math] וזהו בדיוק שיוויון פרסבל.
הוכחת שיוויון פרסבל כאשר טור הפורייה מתכנס במ"ש
- תהי [math]\displaystyle{ f }[/math] רציפה בקטע [math]\displaystyle{ [-\pi,\pi] }[/math] המקיימת [math]\displaystyle{ f(-\pi)=f(\pi) }[/math], כך שהנגזרת שלה [math]\displaystyle{ f' }[/math] רציפה למקוטעין.
- נסמן [math]\displaystyle{ d_n=\sup_{[-\pi,\pi]}|f-S_n| }[/math]
- הוכחנו כי טור הפורייה של f מתכנס אליה במ"ש, כלומר [math]\displaystyle{ d_n\to 0 }[/math].
- לכן [math]\displaystyle{ ||f-S_n||^2 = \frac{1}{\pi}\int_{-\pi}^{\pi} |f-S_n|^2dx \leq 2d_n^2 \to 0 }[/math]
דוגמא
- הפונקציה [math]\displaystyle{ f(x)=x^2 }[/math] מקיימת את דרישות המשפט.
- נזכור כי טור הפורייה שלה הוא:
- [math]\displaystyle{ \frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4(-1)^n}{n^2}cos(nx) }[/math]
- לכן לפי שיוויון פרסבל נקבל כי:
- [math]\displaystyle{ \frac{1}{\pi}\int_{-\pi}^{\pi} x^4dx = \frac{4\pi^4}{18}+\sum_{n=1}^\infty \frac{16}{n^4} }[/math]
- [math]\displaystyle{ \frac{2\pi^4}{5}-\frac{4\pi^4}{18} = \sum_{n=1}^\infty \frac{16}{n^4} }[/math]
- ולכן:
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{1}{n^4} = \frac{\pi^4}{90} }[/math]
הוכחת שיוויון פרסבל במקרה הכללי
- תהי [math]\displaystyle{ f \in E }[/math], אנחנו מעוניינים להוכיח כי [math]\displaystyle{ ||f-S_m||\to 0 }[/math].
- נבנה סדרת פונקציות [math]\displaystyle{ f_n }[/math] רציפות בקטע [math]\displaystyle{ [-\pi,\pi] }[/math] המקיימות [math]\displaystyle{ f_n(-\pi)=f_n(\pi) }[/math], כך שהנגזרות שלהן [math]\displaystyle{ f_n' }[/math] רציפות למקוטעין, המקיימות:
- [math]\displaystyle{ ||f-f_n||\to 0 }[/math]
- יהי [math]\displaystyle{ \varepsilon }[/math], נבחר [math]\displaystyle{ n }[/math] כך ש [math]\displaystyle{ ||f-f_n||\lt \frac{\varepsilon}{2} }[/math].
- נסמן ב[math]\displaystyle{ T_m }[/math] את סדרת הסכומים החלקיים של טור הפורייה של [math]\displaystyle{ f_n }[/math].
- ראינו כי [math]\displaystyle{ \lim_{m\to\infty}||f_n-T_m||=0 }[/math].
- כיוון שההיטל הוא הוקטור הקרוב ביותר, נקבל:
- [math]\displaystyle{ ||f-S_m||\leq ||f-T_m|| }[/math]
- כמו כן, [math]\displaystyle{ ||f-T_m||\leq ||f-f_n||+||f_n-T_m|| }[/math]
- קיים מקום החל ממנו לכל [math]\displaystyle{ m }[/math] מתקיים כי [math]\displaystyle{ ||f_n-T_m||\lt \frac{\varepsilon}{2} }[/math].
- לכן החל ממקום זה [math]\displaystyle{ ||f-S_m||\lt \varepsilon }[/math] כפי שרצינו.
בניית סדרת הפונקציות
- f רציפה למקוטעין, ולכן רציפה במ"ש בכל קטע רציפות.
- לכן ניתן לבחור חלוקה [math]\displaystyle{ P }[/math] הכוללת את נקודות אי הרציפות, עם פרמטר חלוקה מספיק קטן כך ש [math]\displaystyle{ |f(x)-f(c_k)|^2\lt \frac{\varepsilon}{2\pi} }[/math] לכל זוג נקודות [math]\displaystyle{ x,c_k\in [x_{k-1},x_k] }[/math].
- נבחר נקודות כלשהן [math]\displaystyle{ c_k }[/math] בכל קטע ונביט בפונקצית המדרגות g שבכל תת קטע שווה לקבוע [math]\displaystyle{ f(c_k) }[/math].
- כעת האינטגרל תמיד קטן מסכום הדרבו העליון:
- [math]\displaystyle{ \int_{-\pi}^{\pi} |f-g|^2dx \leq \sum_{k=1}^n \sup_{[x_{k-1},x_k]}|f(x)-f(c_k)|^2 (x_k-x_{k-1}) \leq \sum_{k=1}^n \frac{\varepsilon}{2\pi}(x_k-x_{k-1}) = \varepsilon }[/math]
- לכן אפשר לבנות סדרת פונקציות מדרגות כנ"ל [math]\displaystyle{ g_n }[/math] כך ש[math]\displaystyle{ ||f-g_n||\lt \frac{1}{n} }[/math]
- כעת נגדיר סדרת פונקציות [math]\displaystyle{ f_n }[/math] להיות [math]\displaystyle{ g_n }[/math], פרט לשינויים הבאים:
- עבור [math]\displaystyle{ \delta }[/math] שנקבע בהמשך, נחבר בקו ישר את הנקודות בקצוות המקטעים [math]\displaystyle{ [x_k-\delta,x_k] }[/math].
- נגדיר [math]\displaystyle{ f_n(-\pi)=g(\pi) }[/math].
- נחבר בקו ישר את הנקודות בקצה הקטע [math]\displaystyle{ [x_0,x_0+\delta] }[/math].
- עבור [math]\displaystyle{ \delta }[/math] קטנה מספיק, [math]\displaystyle{ \int_{-\pi}^{\pi}|f_n-g|^2dx \lt \frac{1}{n} }[/math].
- סה"כ נקבל כי
- [math]\displaystyle{ f_n }[/math] מורכבת מקטעים ישרים המחוברים זה לזה, ולכן מדובר בפונקציה רציפה, בעלת נגזרת רציפה למקוטעין.
- [math]\displaystyle{ f_n(-\pi)=f_n(\pi) }[/math]
- אכן מתקיים כי [math]\displaystyle{ ||f-f_n||\leq ||f-g||+||g-f_n||\to 0 }[/math]
יחידות טור פורייה
הם ישנן שתי פונקציות שונות בעלות אותו טור פורייה?
- תהיינה [math]\displaystyle{ f,g\in E }[/math] בעלות אותם מקדמי פורייה.
- אם טורי הפורייה מתכנסים לפונקציה, ברור שזו אותה הפונקציה, אבל אם לא?
- מקדמי הפורייה של [math]\displaystyle{ f-g }[/math] הם אפס, ולכן לפי שיוויון פרסבל:
- [math]\displaystyle{ ||f-g||^2=0 }[/math]
- לכן [math]\displaystyle{ f=g }[/math].
- שימו לב שעבור סתם פונקציות רציפות למקוטעין, זה אומר ש[math]\displaystyle{ f=g }[/math] פרט למספר סופי של נקודות.
האם תתכן פונקציה אחת, בעלת שני טורים טריגונומטריים?
- קנטור הוכיח שאם טור טריגונומטרי שווה לאפס בכל הקטע [math]\displaystyle{ [-\pi,\pi] }[/math], אזי כל מקדמי הטור הם אפס.
- יותר מאוחר הוכיחו כי אם הטור מתאפס בכל נקודה בקטע פרט לקבוצה בת מנייה של נקודות, עדיין כל מקדמי הטור הם אפס.
- מנשוב מצא ב1916 טור טריגונומטרי שמתכנס לאפס בכל נקודה פרט לקבוצה ממידה אפס של נקודות, אך לא כל מקדמי הטור הם אפס.
הרצאה 5 - תופעת גיבס, טורי הסינוסים והקוסינוסים
תופעת גיבס
- ראינו תנאים בהם טור הפורייה מתכנס במ"ש.
- כעת אנחנו רוצים לחקור מקרים בהם אין התכנסות במ"ש, ונראה כי בהן יש חריגה מיוחדת של סדרת הסכומי החלקיים מן הפונקציה.
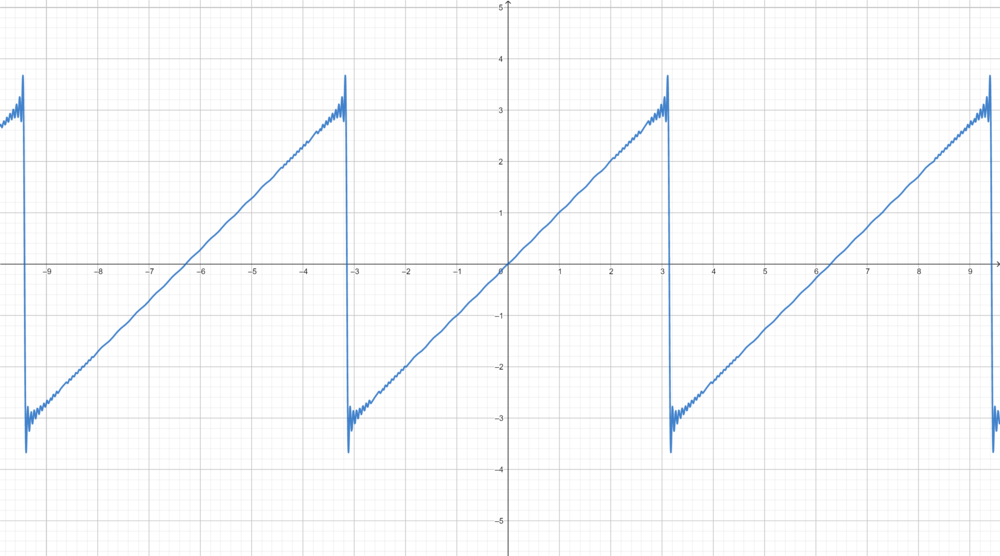
- נביט בטור פורייה של הפונקציה x:
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{2(-1)^{n+1}}{n}\sin(nx) }[/math]
- נסמן ב[math]\displaystyle{ S_m }[/math] את סדרת הסכומים החלקיים של הטור ונביט ב:
- [math]\displaystyle{ S_m(\pi - \frac{\pi}{m})=\sum_{n=1}^m \frac{2(-1)^{n+1}}{n}\sin(n(\pi - \frac{\pi}{m})) = \sum_{n=1}^m \frac{2}{n}\sin(\frac{n\pi}{m}) }[/math]
- כעת,
- [math]\displaystyle{ \sum_{n=1}^m \frac{2}{n}\sin(\frac{n\pi}{m}) = 2\sum_{n=1}^m \frac{\sin\left(\frac{n\pi}{m}\right)}{\left(\frac{n\pi}{m}\right)}\frac{\pi}{m}\to 2\int_0^\pi \frac{\sin(x)}{x}dx }[/math]
- לכן סה"כ השגיאה בקירוב ע"י הסכומים החלקיים בסדרת הנקודות הללו היא:
- [math]\displaystyle{ \pi-\frac{\pi}{m} - S_m (\pi-\frac{\pi}{m}) \to \pi - 2\int_0^\pi \frac{\sin(x)}{x}dx = \int_0^\pi (1-\frac{2\sin(x)}{x})dx \approx -0.56 }[/math]
- (הערכת האינטגרל נעשית על ידי פיתוח טור הטיילור של הפונקציה, נקבל טור לייבניץ לפיו קל לבצע הערכת שגיאה.)
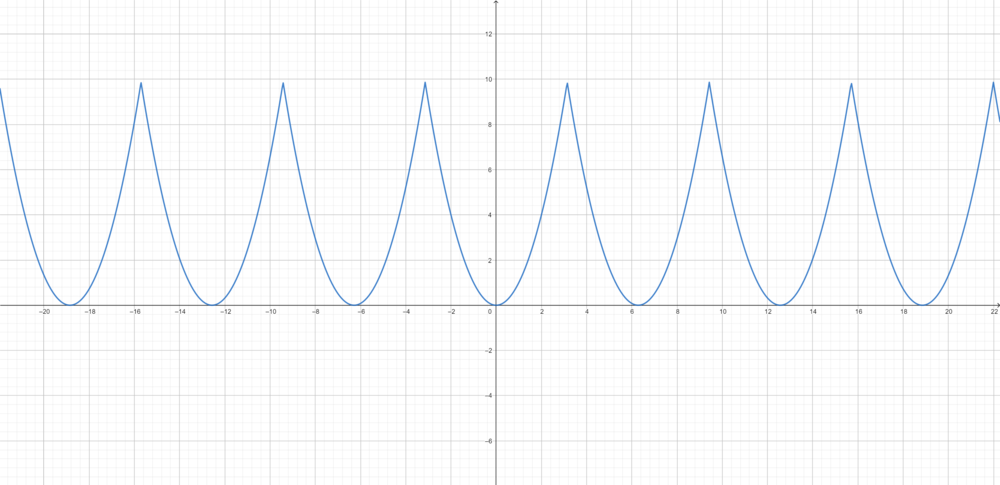
- כלומר סדרת הסכומים החלקיים עולה משמעותית מעל הפונקציה, כפי שניתן לראות בגרף המצורף.
- אם נחלק את זה בגודל הקפיצה בין הגבולות החד צדדים של ההמשך המחזורי של x בנקודה [math]\displaystyle{ \pi }[/math], נקבל בערך [math]\displaystyle{ -0.089 }[/math].
- לא נוכיח זאת, אבל יחס הטעות הזה בנקודות אי הרציפות נשמר באופן כללי עבור פונקציות בE שנגזרתן רציפה למקוטעין, ונקרא 'תופעת גיבס'.
טור הסינוסים וטור הקוסינוסים
- עבור פונקציה [math]\displaystyle{ f }[/math] הרציפה בקטע [math]\displaystyle{ [0,\pi] }[/math] ובעלת נגזרת רציפה למקוטעין, ניתן להשלים אותה לפונקציה [math]\displaystyle{ f^+ }[/math] הזוגית בקטע [math]\displaystyle{ [-\pi,\pi] }[/math], או ל[math]\displaystyle{ f^- }[/math] האי זוגית בקטע [math]\displaystyle{ [-\pi,\pi] }[/math].
- את ההמשך הזוגי אפשר לפתח לטור קוסינוסים, שמתכנס במ"ש בקטע [math]\displaystyle{ [0,\pi] }[/math]. זה נקרא טור הקוסינוסים של הפונקציה [math]\displaystyle{ f }[/math].
- הוכחה:
- [math]\displaystyle{ f^+ }[/math] רציפה ב[math]\displaystyle{ [-\pi,\pi] }[/math], בעלת נגזרת רציפה למקוטעין, ומתקיים כמובן ש[math]\displaystyle{ f(-\pi)=f(\pi) }[/math].
- את ההמשך האי זוגי אפשר לפתח לטור סינוסים, שמתכנס אל הפונקציה בקטע [math]\displaystyle{ (0,\pi) }[/math]. זה נקרא טור הסינוסים של הפונקציה [math]\displaystyle{ f }[/math].
- אם [math]\displaystyle{ f(\pi)=f(0)=0 }[/math] אזי טור הסינוסים מתכנס במ"ש בקטע [math]\displaystyle{ [0,\pi] }[/math].
- הוכחה:
- [math]\displaystyle{ f^- }[/math] רציפה כיוון ש[math]\displaystyle{ f(0)=0 }[/math], ומתקיים כי [math]\displaystyle{ f(-\pi)=-f(\pi)=0=f(\pi) }[/math].
- חישוב המקדמים:
- עבור טור הקוסינוסים:
- [math]\displaystyle{ a_n=\frac{1}{\pi}\int_{-\pi}^{\pi} f^+\cos(nx) dx = \frac{2}{\pi}\int_{0}^{\pi}f\cos(nx)dx }[/math]
- עבור טור הסינוסים:
- [math]\displaystyle{ b_n=\frac{1}{\pi}\int_{-\pi}^{\pi} f^-\cos(nx) dx = \frac{2}{\pi}\int_{0}^{\pi}f\sin(nx)dx }[/math]
דוגמאות
- נחשב טור קוסינוסים של [math]\displaystyle{ e^x }[/math]:
- [math]\displaystyle{ a_0 = \frac{2}{\pi}\int_0^{\pi} e^xdx = \frac{2}{\pi}(e^\pi-1) }[/math]
- [math]\displaystyle{ a_n = \frac{2}{\pi}\int_0^{\pi} e^x\cos(nx)dx = \frac{2}{\pi}\frac{e^\pi(-1)^n-1}{n^2+1} }[/math]
- הטור מתכנס במ"ש לפונקציה בקטע [math]\displaystyle{ [0,\pi] }[/math]:
- [math]\displaystyle{ e^x=\frac{e^\pi-1}{\pi}+ \frac{2}{\pi}\sum_{n=1}^\infty \frac{e^\pi(-1)^n-1}{n^2+1}\cos(nx) }[/math]
- לכן מותר לבצע אינטגרציה איבר איבר, נחשב את [math]\displaystyle{ \int_0^x }[/math] בשני הצדדים ונקבל:
- [math]\displaystyle{ e^x-1 - \frac{e^\pi-1}{\pi}x = \frac{2}{\pi}\sum_{n=1}^\infty \frac{e^\pi(-1)^n-1}{n^3+n}\sin(nx) }[/math]
- נציב למשל [math]\displaystyle{ x=0 }[/math] ונקבל את השיוויון:
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{e^\pi(-1)^n-1}{n^2+1} = \frac{\pi}{2} - \frac{e^\pi-1}{2} }[/math]
- נחשב טור סינוסים של [math]\displaystyle{ e^x }[/math]:
- [math]\displaystyle{ b_n=\frac{2}{\pi}\int_0^\pi e^x\sin(nx)dx = \frac{2n(1-e^\pi(-1)^n)}{\pi(n^2+1)} }[/math]
- הטור מתכנס בקטע [math]\displaystyle{ (0,\pi) }[/math]:
- [math]\displaystyle{ e^x=\sum_{n=1}^\infty \frac{2n(1-e^\pi(-1)^n)}{\pi(n^2+1)}\sin(nx) }[/math]
- נחשב טור סינוסים של [math]\displaystyle{ f(x)=\pi x - x^2 }[/math].
- שימו לב: [math]\displaystyle{ f(0)=f(\pi)=0 }[/math].
- [math]\displaystyle{ b_n=\frac{2}{\pi}\int_0^\pi (\pi x-x^2)\sin(nx)dx = \frac{4(1-(-1)^n)}{\pi n^3} }[/math]
- לכן הטור מתכנס במ"ש בקטע [math]\displaystyle{ [0,\pi] }[/math]:
- [math]\displaystyle{ \pi x - x^2 = \sum_{n=1}^\infty \frac{4(1-(-1)^n)}{\pi n^3} \sin(nx) }[/math]
- לכן מותר לבצע אינטגרציה איבר איבר, נחשב את [math]\displaystyle{ \int_0^x }[/math] בשני הצדדים ונקבל:
- [math]\displaystyle{ \frac{\pi x^2}{2} - \frac{x^3}{3} = \sum_{n=1}^\infty \frac{4(1-(-1)^n)}{\pi n^4}(-\cos(nx)+1) }[/math]
- שימו לב שלא מדובר בטור טריגונומטרי.
הרצאה 6 - משוואת החום על טבעת, התמרת פורייה
משוואת החום על טבעת
- נביט במד"ח החום על מוט עבור הפונקציה [math]\displaystyle{ u(x,t) }[/math]:
- [math]\displaystyle{ u_t-ku_{xx}=0 }[/math]
- [math]\displaystyle{ u(x,0)=f(x) }[/math] (תנאי התחלה)
- [math]\displaystyle{ u(-\pi,t)=u(\pi,t) }[/math] (תנאי שפה)
- [math]\displaystyle{ u_x(-\pi,t)=u_x(\pi,t) }[/math] (תנאי שפה)
- כאשר [math]\displaystyle{ x\in[-\pi,\pi] }[/math], ו[math]\displaystyle{ t\in[0,\infty) }[/math]
- על מנת להבין את תנאי השפה, אפשר לחשוב על הבעייה במובן שהמוט הוא מעגלי.
- נחפש פתרון מהצורה [math]\displaystyle{ u(x,t)=X(x)\cdot T(t) }[/math].
- נציב במד"ח את הניחוש, ונקבל:
- [math]\displaystyle{ X(x)T'(t)=kX''(x)T(t) }[/math]
- נניח שהצדדים שונים מאפס ונחלק:
- [math]\displaystyle{ \frac{T'(t)}{kT(t)}=\frac{X''(x)}{X(x)} }[/math]
- כיוון שכל צד תלוי במשתנה אחר, הדרך היחידה לקבל שיוויון היא אם שני הצדדים קבועים.
- נביט בפתרונות עבור קבוע שלילי:
- [math]\displaystyle{ \frac{T'(t)}{kT(t)}=\frac{X''(x)}{X(x)}=-\lambda }[/math]
- כעת נפתור את המד"רים בנפרד:
- שימו לב שאנו בוחרים את השמות של הקבועים בצורה מיוחדת לקראת הפתרון בהמשך.
- עבור [math]\displaystyle{ \lambda=0 }[/math]:
- [math]\displaystyle{ X_0(x)=cx+\frac{a_0}{2} }[/math], ועל מנת לקיים את תנאי השפה נקבל כי [math]\displaystyle{ c=0 }[/math]
- [math]\displaystyle{ T_0(t)=1 }[/math] (הקבוע יבלע בקבוע של [math]\displaystyle{ X_0(x) }[/math])
- עבור [math]\displaystyle{ \lambda=0 }[/math]:
- עבור [math]\displaystyle{ \lambda\neq 0 }[/math]:
- [math]\displaystyle{ X= a_{\sqrt{\lambda}} \cos(\sqrt{\lambda}x) + b_{\sqrt{\lambda}} \sin(\sqrt{\lambda}x) }[/math]
- [math]\displaystyle{ T=e^{-k\lambda t} }[/math] (הקבוע חסר כי הוא יבלע בקבועים האחרים כאשר נכפול ב[math]\displaystyle{ X(x) }[/math])
- עבור [math]\displaystyle{ \lambda\neq 0 }[/math]:
- ע"י הצבה ניתן לוודא שעבור [math]\displaystyle{ \lambda=n^2 }[/math] הפונקציות לעיל מקיימות את תנאי השפה.
- גם צירוף לינארי שלהן יהווה פתרון כיוון שהמד"ח הומוגנית ותנאי השפה הומוגניים.
- צירוף לינארי אינסופי יהווה פתרון לבעייה אם טורי הנגזרות יתכנסו במ"ש (ולכן יהיה מותר לגזור איבר איבר).
- לכן אנו מחפשים פתרון כללי מהצורה:
- [math]\displaystyle{ u(x,t)=T_0(t)X_0(x)+\sum_{n=1}^\infty T_n(t)X_n(x) = \frac{a_0}{2} + \sum_{n=1}^\infty e^{-kn^2 t}(a_n\cos(nx)+b_n\sin(nx)) }[/math]
- כל שנותר לנו לעשות הוא למצוא את הקבועים [math]\displaystyle{ a_n,b_n }[/math].
- נציב כעת בתנאי ההתחלה [math]\displaystyle{ u(x,0)=f(x) }[/math] ונקבל בעצם את טור הפורייה:
- [math]\displaystyle{ f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx) }[/math]
- אנחנו יכולים לפתור משוואה זו בהנתן שf מקיימת את תנאי משפט דיריכלה.
- מדוע זה יהיה פתרון?
- נזכור שמקדמי הפורייה שואפים לאפס.
- בזכות האקספוננט, טור זה ונגזרותיו אכן יתכנסו במ"ש עבור [math]\displaystyle{ t\in [a,\infty) }[/math] לכל [math]\displaystyle{ a\gt 0 }[/math] ולכל [math]\displaystyle{ x\in[-\pi,\pi] }[/math].
- לכן מותר לגזור איבר איבר, ואכן מדובר בפתרון של המד"ח.
התמרת פורייה
טור פורייה המרוכב
- לא קשה לוודא כי [math]\displaystyle{ \{e^{inx}\}_{n\in\mathbb{Z}} }[/math] מהווה קבוצה אורתונורמלית בE אם נעדכן מעט את המכפלה הפנימית:
- [math]\displaystyle{ \langle f,g\rangle = \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)\overline{g(x)}dx }[/math]
- תהי [math]\displaystyle{ f\in E }[/math], שאלה שעולה באופן טבעי היא האם:
- [math]\displaystyle{ f=\sum_{n=-\infty}^\infty \langle f,e^{inx}\rangle e^{inx} }[/math]
- כאשר אנו מגדירים את הסכום ממינוס אינסוף עד אינסוף באופן הבא:
- [math]\displaystyle{ \sum_{n=-\infty}^\infty u_n = u_0+\sum_{n=1}^\infty (u_n+u_{-n}) }[/math]
- נסמן את מקדמי פורייה הרגילים ב[math]\displaystyle{ a_n,b_n }[/math].
- נשים לב כי עבור [math]\displaystyle{ n=0 }[/math] נקבל:
- [math]\displaystyle{ \langle f,1\rangle = \frac{a_0}{2} }[/math]
- כעת עבור [math]\displaystyle{ n\gt 0 }[/math] מתקיים:
- [math]\displaystyle{ \langle f, e^{inx}\rangle e^{inx}+\langle f, e^{-inx}\rangle e^{-inx} = }[/math]
- [math]\displaystyle{ = (\langle f, e^{inx}\rangle+\langle f, e^{-inx}\rangle)\cos(nx) + (\langle f, e^{inx}\rangle-\langle f, e^{-inx}\rangle)i\sin(nx)= }[/math]
- [math]\displaystyle{ = 2\langle f, \cos(nx)\rangle \cos(nx) + 2\langle f, i\sin(nx)\rangle i\sin(nx)= }[/math]
- [math]\displaystyle{ =a_n\cos(nx)+b_n\sin(nx) }[/math]
- (שימו לב: הi יצא מהצד הימני של המכפלה הפנימית עם מינוס)
- כלומר, טור פורייה המרוכב הוא בדיוק טור פורייה הרגיל!
הכללה לפונקציות שאינן מחזוריות
- טורי פורייה עזרו לנו לחקור פונקציות בקטע [math]\displaystyle{ [-\pi,\pi] }[/math].
- בהנתן גל [math]\displaystyle{ e^{inx} }[/math], מצאנו את ה'אמפליטודה' שלו (המקדם):
- [math]\displaystyle{ \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)e^{-inx}dx }[/math]
- (שימו לב - המכפלה הפנימית מצמידה את הפונקציה מימין, ולכן קיבלנו [math]\displaystyle{ -i }[/math]).
- מחשבה הגיונית היא שאם נרצה לחקור פונקציות בכל הממשיים, עבור גל [math]\displaystyle{ e^{isx} }[/math] נמצא את ה'אמפליטודה':
- [math]\displaystyle{ \mathcal{F}[f](s)=\frac{1}{2\pi}\int_{-\infty}^\infty f(x)e^{-isx}dx }[/math].
- כאשר האינטגרל מתכנס, הפונקציה [math]\displaystyle{ \mathcal{F}[f](s) }[/math] נקראת התמרת פורייה של הפונקציה [math]\displaystyle{ f }[/math].
- הערה - המקדם [math]\displaystyle{ \frac{1}{2\pi} }[/math] לעיתים אינו מופיע בהגדרת ההתמרה. אנחנו נראה בהמשך שיש לו קשר להתמרה ההפוכה.
- הערות כלליות:
- נסמן בדר"כ את ההתמרה של f ב[math]\displaystyle{ F(s)=\mathcal{F}(f)(s) }[/math].
- [math]\displaystyle{ F(s) }[/math] מייצגת את האמפליטודה בכל תדר, ולכן נהוג לומר שהיא מוגדרת ב'מרחב התדר'.
- לעומת זאת, [math]\displaystyle{ f(x) }[/math] מייצגת את גובה הפונקציה בכל נקודה בזמן, ונהוג לומר שהיא מוגדרת ב'מרחב הזמן'.
- לכל תדר [math]\displaystyle{ s }[/math] יש שני גלים שמייצגים אותו, [math]\displaystyle{ e^{\pm isx} }[/math].
- כפי שלמדנו, באמצעות שני הגלים ניתן לייצג כל 'פאזה'.
- נסמן ב[math]\displaystyle{ G }[/math] את אוסף הפונקציות [math]\displaystyle{ g }[/math] הרציפות למקוטעין ב[math]\displaystyle{ \mathbb{R} }[/math], עבורן האינטגרל הלא אמיתי מתכנס [math]\displaystyle{ \int_{-\infty}^\infty|g(x)|dx\lt \infty }[/math].
- לכל [math]\displaystyle{ f\in G }[/math] התמרת הפורייה מוגדרת בכל הממשיים.
- הוכחה:
- [math]\displaystyle{ \int_{-\infty}^\infty|f(x)e^{-isx}|dx = \int_{-\infty}^\infty|f(x)|dx }[/math] מתכנס.
- כיוון שהאינטגרל המגדיר את [math]\displaystyle{ F(s) }[/math] מתכנס בהחלט, הוא מתכנס.
דוגמאות
- נמצא את [math]\displaystyle{ \mathcal{F}(f)(s) }[/math] עבור [math]\displaystyle{ f(x)=e^{-|x|} }[/math].
- [math]\displaystyle{ 2\pi F(s)=\int_{-\infty}^\infty e^{-|x|}e^{-isx}dx = \int_0^\infty e^{-x}e^{-isx}dx + \int_{-\infty}^0 e^{x}e^{-isx}dx= }[/math]
- [math]\displaystyle{ =\left[\frac{e^{-x(1+is)}}{-(1+is)}\right]_0^\infty + \left[\frac{e^{x(1-is)}}{1-is}\right]_{-\infty}^0=\frac{1}{1+is} + \frac{1}{1-is} = \frac{2}{1+s^2} }[/math]
- שימו לב - השתמשנו בעובדה ש[math]\displaystyle{ e^{isx} }[/math] חסומה, ואילו [math]\displaystyle{ e^{-x}\to 0 }[/math] כאשר [math]\displaystyle{ x\to \infty }[/math].
- לכן סה"כ קיבלנו כי [math]\displaystyle{ \mathcal{F}[e^{-|x|}](s) = \frac{1}{\pi(1+s^2)} }[/math]
- נמצא את התמרת הפורייה של [math]\displaystyle{ f(x)=\begin{cases}|x| & |x|\leq \pi \\ 0 & |x|\gt \pi\end{cases} }[/math]
- [math]\displaystyle{ F(s)=\frac{1}{2\pi}\int_{-\infty}^\infty f(x)e^{-isx}dx = \frac{1}{2\pi}\int_{-\pi}^\pi |x|e^{-isx}dx = }[/math]
- [math]\displaystyle{ \frac{1}{2\pi}\int_{-\pi}^\pi |x|\cos(sx)dx - \frac{i}{2\pi}\int_{-\pi}^\pi |x|\sin(sx)dx = \frac{1}{\pi}\int_{0}^\pi x\cos(sx)dx = \frac{\sin(s\pi)}{s} + \frac{\cos(s\pi)-1}{s^2\pi} }[/math]
הרצאה 7 - תכונות של התמרות פורייה
תכונות ההתמרה
- תהי [math]\displaystyle{ f\in G }[/math] אזי [math]\displaystyle{ F(s)=\mathcal{F}[f](s) }[/math] רציפה במ"ש ב[math]\displaystyle{ \mathbb{R} }[/math].
- הוכחה:
- יהי [math]\displaystyle{ \varepsilon\gt 0 }[/math]. כיוון ש [math]\displaystyle{ \int_{-\infty}^{\infty}|f(x)|dx }[/math] מתכנס, קיים [math]\displaystyle{ R }[/math] עבורו [math]\displaystyle{ \frac{1}{2\pi}\int_{|x|\gt R}|f(x)|dx \lt \frac{\varepsilon}{4} }[/math]
- עבור [math]\displaystyle{ s_1,s_2 }[/math] מתקיים כי [math]\displaystyle{ |F(s_1)-F(s_2)|\leq \frac{1}{2\pi}\int_{-\infty}^{\infty}|f(x)(e^{-is_1x}-e^{-is_2x})|dx }[/math]
- כמובן ש [math]\displaystyle{ |e^{-is_1x}-e^{-is_2x}|\leq 2 }[/math] ולכן בתחום [math]\displaystyle{ |x|\gt R }[/math] האינטגרל הנ"ל קטן מ[math]\displaystyle{ \frac{\varepsilon}{2} }[/math].
- נותר להוכיח שעבור [math]\displaystyle{ s_1,s_2 }[/math] מספיק קרובים מתקיים כי [math]\displaystyle{ \frac{1}{2\pi}\int_{-R}^{R}|f(x)(e^{-is_1x}-e^{-is_2x})|dx\lt \frac{\varepsilon}{2} }[/math]
- נראה כי [math]\displaystyle{ |e^{ix}-e^{iy}|\leq |x-y| }[/math].
- [math]\displaystyle{ |e^{ix}-e^{iy}| }[/math] הוא המרחק בין שתי נקודות על מעגל היחידה.
- [math]\displaystyle{ |x-y| }[/math] הוא הזווית בינהן, כלומר אורך הקשת בינהן.
- אורך הקשת בוודאי גדול או שווה למרחק הישר בין שתי הנקודות.
- לכן [math]\displaystyle{ |e^{-is_1x}-e^{-is_2x}|\leq |x||s_1-s_2| }[/math]
- כיוון ש[math]\displaystyle{ |x|\leq R }[/math] והפונקציה [math]\displaystyle{ f }[/math] חסומה בתחום זה, עבור [math]\displaystyle{ |s_1-s_2| }[/math] מספיק קטן נקבל את הדרוש.
- רשימת תכונות נוספות של ההתמרה:
- [math]\displaystyle{ \mathcal{F}[f+a\cdot g] = \mathcal{F}[f]+a\mathcal{F}[g] }[/math]
- [math]\displaystyle{ \mathcal{F}[f](-s) = \overline{\mathcal{F}[f](s)} }[/math]
- אם [math]\displaystyle{ f }[/math] ממשית וזוגית, גם [math]\displaystyle{ \mathcal{F}[f](s) }[/math] ממשית וזוגית.
- הזזה במרחב הזמן:
- אם [math]\displaystyle{ g(x)=f(ax+b) }[/math], אזי [math]\displaystyle{ \mathcal{F}(g)(s) = \frac{1}{|a|}e^{\frac{isb}{a}}\mathcal{F}[f](\frac{s}{a}) }[/math]
- אם [math]\displaystyle{ a=1 }[/math] אז נקבל שהזזה במרחב הזמן שקולה לסיבוב במרחב התדר (כפל ב[math]\displaystyle{ e^{isb} }[/math] משנה את הזוית).
- הזזה במרחב התדר:
- [math]\displaystyle{ \mathcal{F}[e^{ibx}f(x)](s) = \mathcal{F}[f](s-b) }[/math]
- באופן דומה, קיבלנו שסיבוב בזמן שקול להזזה בתדר.
- התמרת הנגזרת:
- נניח [math]\displaystyle{ f,f'\in G }[/math] ונניח כי [math]\displaystyle{ \lim_{x\to \pm\infty}f(x)=0 }[/math], אזי:
- [math]\displaystyle{ \mathcal{F}[f'](s)=is\mathcal{F}[f](s) }[/math]
- הוכחה:
- [math]\displaystyle{ \mathcal{F}[f'](s) = \frac{1}{2\pi}\int_{-\infty}^{\infty} f'(x)e^{-isx}dx }[/math]
- נבצע אינטגרציה בחלקים ונקבל כי
- [math]\displaystyle{ \mathcal{F}[f'](s) = \frac{1}{2\pi}(fe^{-isx})_{-\infty}^{\infty} + \frac{is}{2\pi} \int_{-\infty}^{\infty} f(x)e^{-isx}dx }[/math].
- כיוון ש[math]\displaystyle{ e^{-isx} }[/math] חסומה, יחד עם הנתון נובע כי [math]\displaystyle{ (fe^{-isx})_{-\infty}^{\infty}=0 }[/math].
- לכן סה"כ קיבלנו כי [math]\displaystyle{ \mathcal{F}[f'](s)=is\mathcal{F}[f](s) }[/math]
- נגזרת ההתמרה:
- תהי [math]\displaystyle{ f\in G }[/math] רציפה כך ש[math]\displaystyle{ xf(x)\in G }[/math] אזי:
- [math]\displaystyle{ \mathcal{F}[xf(x)](s)=i\frac{d}{ds}\mathcal{F}[f](s) }[/math]
- הוכחה:
- [math]\displaystyle{ i\frac{d}{ds}\mathcal{F}[f](s) = i \frac{d}{ds} \frac{1}{2\pi}\int_{-\infty}^{\infty} f(x)e^{-isx}dx = \frac{i}{2\pi}\int_{-\infty}^{\infty} f(x)\frac{d}{ds}e^{-isx}dx = \frac{-i^2}{2\pi}\int_{-\infty}^{\infty} xf(x)e^{-isx} = \mathcal{F}[xf(x)](s) }[/math]
- אנחנו צריכים להצדיק את ההכנסה של הנגזרת אל תוך האינטגרל:
- נסמן [math]\displaystyle{ F_n(s)=\frac{1}{2\pi}\int_{-n}^{n} f(x)e^{-isx}dx }[/math]
- ברור ש[math]\displaystyle{ F_n(s)\to F(s) }[/math], נוכיח שסדרת הנגזרות מתכנסת במ"ש ולכן מתכנסת לנגזרת של [math]\displaystyle{ F(s) }[/math].
- עבור אינטגרל סופי מותר להחליף את סדר הנגזרת והאינטגרל בזכות פוביני.
- אכן [math]\displaystyle{ F_n'(s) }[/math] מתכנסות במ"ש כיוון שהאינטגרל [math]\displaystyle{ \int_{-\infty}^\infty |xf(x)|dx }[/math] מתכנס, והרי [math]\displaystyle{ |xf(x)e^{-isx}|=|xf(x)| }[/math] ואכן אינו תלוי בs.
דוגמאות
- ראינו כי [math]\displaystyle{ \mathcal{F}[e^{-|x|}](s) = \frac{1}{\pi(1+s^2)} }[/math]
- לכן על ידי הזזה בזמן נקבל כי:
- [math]\displaystyle{ \mathcal{F}[e^{-|1-2x|}](s) = \frac{e^{\frac{-is}{2}}}{2\pi (1+(-\frac{s}{2})^2)} }[/math]
- נסמן [math]\displaystyle{ F(s)=\mathcal{F}[e^{-x^2}] }[/math].
- כעת [math]\displaystyle{ \mathcal{F}[xe^{-x^2}] = iF' }[/math] לפי הנוסחא של נגזרת ההתמרה.
- מצד שני, [math]\displaystyle{ \mathcal{F}[-2xe^{-x^2}] = isF }[/math] לפי הנוסחא של התמרת הנגזרת.
- ביחד נקבל כי [math]\displaystyle{ isF = -2iF' }[/math], ולכן [math]\displaystyle{ sF=-2F' }[/math].
- נפתור את המד"ר:
- נכפול בגורם אינטגרציה [math]\displaystyle{ \frac{1}{2}e^{\frac{s^2}{4}} }[/math] ונקבל [math]\displaystyle{ (e^{\frac{s^2}{4}}F)'=0 }[/math]
- לכן [math]\displaystyle{ F=Ce^{-\frac{s^2}{4}} }[/math]
- נציב [math]\displaystyle{ s=0 }[/math]
- [math]\displaystyle{ 2\pi C=F(0)=\int_{-\infty}^\infty e^{-x^2}dx }[/math], נחשב אינטגרל מפורסם זה בהמשך.
הרצאה 8 - התמרה הפוכה
- בטורי פורייה, מקדמי הפורייה היו האמפליטודות של התדרים, וכאשר סכמנו את הגלים קיבלנו חזרה את הפונקציה לפי משפט דיריכלה.
- כעת התדרים שלנו הם כל הממשיים, ולכן הסכימה שלהם היא בעצם אינטגרל.
- האמפליטודה של כל תדר מרוכב [math]\displaystyle{ e^{isx} }[/math] היא התמרת הפורייה [math]\displaystyle{ F(s) }[/math], ולכן אנחנו מצפים לקבל:
- [math]\displaystyle{ f(x)=\int_{-\infty}^\infty F(s)e^{isx}ds=\mathcal{F}^{-1}[F](x) }[/math]
- משפט ההתמרה ההפוכה:
- תהי [math]\displaystyle{ f\in G }[/math], אזי בכל נקודה בה קיימות הנגזרות החד צדדיות מתקיים כי:
- [math]\displaystyle{ \frac{f(x^+)+f(x^-)}{2}=\lim_{n\to\infty}\int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\mathcal{F}[f](s)e^{isx}ds }[/math]
- שימו לב שהאינטגרל [math]\displaystyle{ \int_{-\infty}^{\infty}\mathcal{F}[f](s)e^{isx}ds }[/math] לא חייב להתכנס, אבל אם הוא מתכנס הוא שווה לגבול לעיל.
דוגמא
- ראינו ש[math]\displaystyle{ \mathcal{F}[e^{-x^2}] = Ce^{-\frac{s^2}{4}} =\frac{1}{2\pi}\int_{-\infty}^\infty e^{-x^2}e^{-isx}dx }[/math]
- כיוון ש[math]\displaystyle{ e^{-x^2} }[/math] רציפה וגזירה, וכיוון ש [math]\displaystyle{ e^{-\frac{s^2}{4}}\in G }[/math] לפי משפט ההתמרה ההפוכה נקבל כי:
- [math]\displaystyle{ \mathcal{F}^{-1}[Ce^{-\frac{s^2}{4}}](x) = e^{-x^2} }[/math]
- כלומר [math]\displaystyle{ e^{-x^2}=\int_{-\infty}^\infty Ce^{-\frac{s^2}{4}}e^{-isx}ds }[/math]
- נציב [math]\displaystyle{ t=\frac{s}{2} }[/math] ונקבל:
- [math]\displaystyle{ e^{-x^2} = 2C\int_{-\infty}^\infty e^{-t^2}e^{-i(-2x)t}dt = 2C\cdot 2\pi Ce^{-\frac{(-2x)^2}{4}} }[/math]
- ולכן [math]\displaystyle{ 4C^2\pi = 1 }[/math], ומכאן [math]\displaystyle{ C=\frac{1}{2\sqrt{\pi}} }[/math]
- נזכור בנוסף שראינו כי [math]\displaystyle{ 2\pi C = \int_{-\infty}^\infty e^{-x^2}dx }[/math].
- לכן נובע כי [math]\displaystyle{ \int_{-\infty}^\infty e^{-x^2}dx = \sqrt{\pi} }[/math]
הקדמה לקראת הוכחת משפט ההתמרה ההפוכה
- כעת נוכיח מספר טענות הדרושות לנו לצורך הוכחת משפט ההתמרה ההפוכה.
למת רימן-לבג
- ראינו גרסא של למת רימן-לבג עבור טורי פוריה, לפי מקדמי הפורייה שואפים לאפס.
- כעת ננסח ונוכיח גרסא עבור התמרות פורייה:
- תהי [math]\displaystyle{ f\in G }[/math], אזי [math]\displaystyle{ \lim_{s\to\pm\infty}\mathcal{F}[f](s)=0 }[/math]
- (כלומר, האמפליטודות שואפות לאפס כאשר התדר שואף לאינסוף)
- נוכיח את הלמה:
- צ"ל כי[math]\displaystyle{ \lim_{s\to\pm\infty}\frac{1}{2\pi}\int_{-\infty}^\infty f(x)e^{-isx}dx =0 }[/math]
- נשים לב כי [math]\displaystyle{ e^{-isx}=\cos(sx)-i\sin(sx) }[/math].
- לכן מספיק לנו להוכיח כי [math]\displaystyle{ \lim_{s\to\pm\infty}\frac{1}{2\pi}\int_{-\infty}^\infty f(x)\cos(sx)dx =0 }[/math] (ההוכחה עבור סינוס דומה).
- כיוון ש[math]\displaystyle{ f\in G }[/math] האינטגרל [math]\displaystyle{ \int_{-\infty}^{\infty}|f(x)|dx }[/math] מתכנס.
- לכן קיים [math]\displaystyle{ M }[/math] עבורו [math]\displaystyle{ \int_{|x|\gt M}|f(x)|dx\lt \frac{\varepsilon}{2} }[/math].
- לכן [math]\displaystyle{ |\int_{|x|\gt M}f(x)\cos(sx)dx|\leq \int_{|x|\gt M}|f(x)|dx \lt \frac{\varepsilon}{2} }[/math]
- לכן מספיק לנו להוכיח כי עבור [math]\displaystyle{ |s| }[/math] מספיק גדול מתקיים [math]\displaystyle{ |\int_{-M}^{M}f(x)\cos(sx)dx| \lt \frac{\varepsilon}{2} }[/math]
- (עבור [math]\displaystyle{ M=\pi }[/math] ו[math]\displaystyle{ s\in\mathbb{N} }[/math] כבר הוכחנו טענה זו בעזרת פרסבל, כעת נשתמש בשיטות אחרות.)
- נשים לב כי בכל קטע מתקיים:
- [math]\displaystyle{ \lim_{s\to\pm\infty}\int_{x_1}^{x_2}\cos(sx)dx = \lim_{s\to\pm\infty}\frac{\sin(sx_2)-\sin(sx_1)}{s}=0 }[/math]
- כיוון ש[math]\displaystyle{ f }[/math] רציפה למקוטעין היא אינטגרבילית ב[math]\displaystyle{ [-M,M] }[/math].
- לכן ניתן לבחור פונקצית מדרגות [math]\displaystyle{ h }[/math] עבורה מתקיים [math]\displaystyle{ \int_{-M}^M |f-h|dx \lt \frac{\varepsilon}{4} }[/math] (האינטגרל על פונקצית המדרגות הינו סכום דרבו תחתון מספיק קרוב).
- כמו כן מתקיים:
- [math]\displaystyle{ \int_{-M}^Mh\cos(sx)dx = \sum \int_{x_{i-1}}^{x_i}m_i\cos(sx)dx }[/math]
- כיוון שמדובר בסכום סופי של ביטויים ששואפים לאפס, הסכום גם שואף לאפס.
- סה"כ [math]\displaystyle{ \int_{-M}^{M}f(x)\cos(sx)dx = \int_{-M}^{M}(f(x)-h(x))\cos(sx)dx + \int_{-M}^{M}h(x)\cos(sx)dx }[/math]
- מתקיים כי [math]\displaystyle{ |\int_{-M}^{M}(f(x)-h(x))\cos(sx)dx|\leq \int_{-M}^{M}|f(x)-h(x)|dx \lt \frac{\varepsilon}{4} }[/math]
- עבור [math]\displaystyle{ |s| }[/math] מספיק גדול מתקיים כי [math]\displaystyle{ |\int_{-M}^{M}h(x)\cos(sx)dx|\lt \frac{\varepsilon}{4} }[/math]
- סה"כ קיבלנו כי עבור [math]\displaystyle{ |s| }[/math] מספיק גדול מתקיים [math]\displaystyle{ |\int_{-\infty}^{\infty}f(x)\cos(sx)sx|\lt \varepsilon }[/math]
טענת עזר
- תהי [math]\displaystyle{ f\in G }[/math] ותהי x נק' בה הנגזרות החד צדדיות קיימות, אזי:
- [math]\displaystyle{ \lim_{n\to\infty} \frac{1}{\pi}\int_0^{\infty} f(x+t)\frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{f(x^+)}{2} }[/math]
- [math]\displaystyle{ \lim_{n\to\infty} \frac{1}{\pi}\int_{-\infty}^{0} f(x+t)\frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{f(x^-)}{2} }[/math]
- נוכיח את הטענה הראשונה, הטענה השנייה דומה.
- נגדיר את הפונקציה [math]\displaystyle{ g(t)=\begin{cases}\frac{f(x+t)}{t}& x\in [\pi,\infty)\\ 0 & x\in (-\infty,\pi)\end{cases} }[/math]
- כיוון ש[math]\displaystyle{ f\in G }[/math] נובע שגם [math]\displaystyle{ g\in G }[/math] הרי [math]\displaystyle{ \left|\frac{f(x+t)}{t}\right|\leq |f(x+t)| }[/math] עבור [math]\displaystyle{ t\gt \pi }[/math].
- לכן לפי למת רימן-לבג נובע כי [math]\displaystyle{ \lim_{s\to\infty}\int_{-\infty}^{\infty}g(t)\sin(st)dt = 0 }[/math]
- בפרט מתקיים גבול הסדרה:
- [math]\displaystyle{ \lim_{n\to\infty} \int_{-\infty}^{\infty}g(t)\sin\left((n+\frac{1}{2})t\right)dt =0 }[/math]
- אבל [math]\displaystyle{ \int_{-\infty}^{\infty}g(t)\sin\left((n+\frac{1}{2})t\right)dt = \int_\pi^\infty \frac{f(x+t)}{t}\sin\left((n+\frac{1}{2})t\right)dt }[/math]
- לכן נותר להוכיח כי [math]\displaystyle{ \lim_{n\to\infty}\frac{1}{\pi}\int_0^{\pi} f(x+t)\frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{f(x^+)}{2} }[/math]
- נגדיר את הפונקציה [math]\displaystyle{ h(t)=f(x+t)\frac{2\sin(\frac{t}{2})}{t} }[/math].
- אם נתקן את אי הרציפות הסליקה של [math]\displaystyle{ \frac{2\sin(\frac{t}{2})}{t} }[/math] נקבל טור טיילור שגזיר אינסוף פעמים.
- לכן הפוקנציה [math]\displaystyle{ h }[/math] רציפה למקוטעין ובעלת נגזרות חד צדדיות קיימות.
- כעת נשים לב כי:
- [math]\displaystyle{ \frac{1}{\pi}\int_0^{\pi} f(x+t)\frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{1}{\pi}\int_0^{\pi} h(t)\frac{\sin\left((n+\frac{1}{2})t\right)}{2\sin(\frac{t}{2})}dt = \frac{1}{\pi}\int_0^{\pi} h(t)D_n(t)dt }[/math]
- לפי ההוכחה של משפט דיריכלה להתכנסות טורי פורייה, הגבול של הביטוי הזה שווה ל[math]\displaystyle{ \frac{h(0^+)}{2} = \frac{f(x^+)}{2} }[/math].
דוגמא
- טענה:
- [math]\displaystyle{ \int_0^\infty \frac{\sin(x)}{x}dx = \frac{\pi}{2} }[/math]
- הוכחה:
- ראשית, אנו יודעים כי האינטגרל מתכנס לפי מבחן דיריכלה לאינטגרלים לא אמיתיים.
- לכן מתקיים כי [math]\displaystyle{ \int_0^\infty \frac{\sin(x)}{x}dx =\lim_{n\to\infty} \int_0^{(n+\frac{1}{2})\pi}\frac{\sin(x)}{x}dx }[/math]
- נבצע הצבה [math]\displaystyle{ t=\frac{x}{n+\frac{1}{2}} }[/math] ונקבל כי:
- [math]\displaystyle{ \int_0^{(n+\frac{1}{2})\pi}\frac{\sin(x)}{x}dx = \int_0^\pi \frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt }[/math]
- עבור [math]\displaystyle{ f(x)=1 }[/math], לפי הוכחת טענת העזר נקבל כי הגבול הוא [math]\displaystyle{ \frac{\pi}{2} }[/math]
הוכחת משפט ההתמרה ההפוכה
- [math]\displaystyle{ \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\mathcal{F}[f](s)e^{isx}ds = \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\left[\frac{1}{2\pi}\int_{-\infty}^\infty f(y)e^{-isy}dy\right]e^{isx}ds= }[/math]
- [math]\displaystyle{ =\frac{1}{2\pi} \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\int_{-\infty}^\infty f(y)e^{is(x-y)}dyds }[/math]
- נחליף את סדר האינטגרציה (הצדקה בהמשך), ונקבל:
- [math]\displaystyle{ \frac{1}{2\pi}\int_{-\infty}^\infty\int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}f(y)e^{is(x-y)}dsdy = }[/math]
- [math]\displaystyle{ \frac{1}{2\pi}\int_{-\infty}^\infty f(y) \left[\frac{e^{is(x-y)}}{i(x-y)}\right]_{-(n+\frac{1}{2})}^{n+\frac{1}{2}} dy = }[/math]
- [math]\displaystyle{ \frac{1}{2\pi}\int_{-\infty}^\infty f(y) \frac{2\sin\left((n+\frac{1}{2})(x-y)\right)}{(x-y)} dy }[/math]
- נציב [math]\displaystyle{ t=y-x }[/math] ונקבל:
- [math]\displaystyle{ \frac{1}{\pi}\int_{-\infty}^\infty f(x+t) \frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{f(x^+)+f(x^-)}{2} }[/math]
כאשר המעבר האחרון הוא בזכות טענת העזר לעיל.
הצדקת החלפת סדר האינטגרציה
- נביט בסדרה [math]\displaystyle{ u_k(s)=\int_{-k}^k f(y)e^{is(x-y)}dy }[/math], שמתכנסת כמובן ל[math]\displaystyle{ \int_{-\infty}^\infty f(y)e^{is(x-y)}dy }[/math]
- מתקיים כי [math]\displaystyle{ |\int_{-\infty}^\infty f(y)e^{is(x-y)}dy - u_k(s)| \leq \int_{|y|\gt k} |f(y)e^{is(x-y)}|dy = \int_{|y|\gt k} |f(y)|dy\to 0 }[/math]
- (נתון כי [math]\displaystyle{ f\in G }[/math])
- לכן הסדרה מתכנסת במ"ש ומותר לבצע אינטגרציה איבר איבר:
- [math]\displaystyle{ \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\int_{-\infty}^\infty f(y)e^{is(x-y)}dyds = \lim_{k\to\infty} \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}} u_k(s)ds }[/math]
- לפי פוביני מותר לנו להחליף את סדר האינטגרציה ונקבל כי
- [math]\displaystyle{ \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\int_{-\infty}^\infty f(y)e^{is(x-y)}dyds = \lim_{k\to\infty} \int_{-k}^k \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}f(y)e^{is(x-y)}dsdy = \int_{-\infty}^\infty \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}f(y)e^{is(x-y)}dsdy }[/math]
- שימו לב שהאינטגרל הלא אמיתי אכן מתכנס (כפי שהוכחנו לעיל) ולכן שווה לגבול.
הרצאה 9 - קונבולוציה
- תהיינה [math]\displaystyle{ f,g:\mathbb{R}\to\mathbb{C} }[/math] פונקציות, נגדיר את הקונבולוציה ביניהן להיות:
- [math]\displaystyle{ f*g(x) = \int_{-\infty}^\infty f(x-y)g(y)dy }[/math].
- מוטיבציה לדוגמא:
- אם [math]\displaystyle{ f,g }[/math] הן פונקציות צפיפות של משתנים מקריים, מהי פונקציית הצפיפות של סכום המשתנים?
- הסיכוי שסכום המשתנים יהיה x, הוא סכום מכפלות הסיכויים שמשתנה אחד יהיה שווה y והשני יהיה שווה x-y.
- הקונבולוציה היא אבלית:
- [math]\displaystyle{ g*f = \int_{-\infty}^\infty g(x-y)f(y)dy = \{t=x-y,dt=-dy\} = \int_{-\infty}^\infty g(t)f(x-t)dt = f*g }[/math]
- שימו לב: בנושא זה נבצע החלפת סדר אינטגרציה מספר פעמים, אך לא נצדיק החלפות אלו כיוון שהן דורשות העמקה רבה.
- ניתן להעמיק ע"י קריאה בספר Fourier Analysis של T.W.Korner
- משפט הקונבולוציה:
- תהיינה [math]\displaystyle{ f,g\in G }[/math] רציפות וחסומות אזי [math]\displaystyle{ \mathcal{F}[f*g] = 2\pi \cdot \mathcal{F}[f] \cdot \mathcal{F}[g] }[/math]
- הסבר המשפט (לא הוכחה מלאה, כיוון שאנו מחליפים סדר אינטגרציה ללא הצדקה):
- [math]\displaystyle{ \mathcal{F}[f*g] = \frac{1}{2\pi}\int_{-\infty}^\infty \left[\int_{-\infty}^\infty f(x-y)g(y)dy\right]e^{-isx}dx = }[/math]
- [math]\displaystyle{ = \frac{1}{2\pi}\int_{-\infty}^\infty \int_{-\infty}^\infty f(x-y)e^{-is(x-y)}g(y)e^{-isy}dydx = }[/math]
- [math]\displaystyle{ = \frac{1}{2\pi}\int_{-\infty}^\infty \int_{-\infty}^\infty f(x-y)e^{-is(x-y)}g(y)e^{-isy}dxdy = }[/math]
- [math]\displaystyle{ = \frac{1}{2\pi}\int_{-\infty}^\infty \left[\int_{-\infty}^\infty f(x-y)e^{-is(x-y)}dx\right] g(y)e^{-isy}dy = }[/math]
- [math]\displaystyle{ = \frac{1}{2\pi}\int_{-\infty}^\infty \left[\int_{-\infty}^\infty f(t)e^{-ist}dt\right] g(y)e^{-isy}dy = }[/math]
- [math]\displaystyle{ = \left(2\pi\frac{1}{2\pi}\int_{-\infty}^\infty f(t)e^{-ist}dt\right) \cdot \left( \frac{1}{2\pi}\int_{-\infty}^\infty g(y)e^{-isy}dy\right) =2\pi \cdot \mathcal{F}[f] \cdot \mathcal{F}[g] }[/math]