חתכי דדקינד

הקדמה

• אנחנו מעוניינים שבמערכת המספרים שלנו יהיה פתרון למשוואה [math]\displaystyle{ x^2=2 }[/math] (שורש שתיים).

• הרי אחרת, מה המרחק מהנקודה [math]\displaystyle{ (1,1) }[/math] לראשית הצירים [math]\displaystyle{ (0,0) }[/math]?

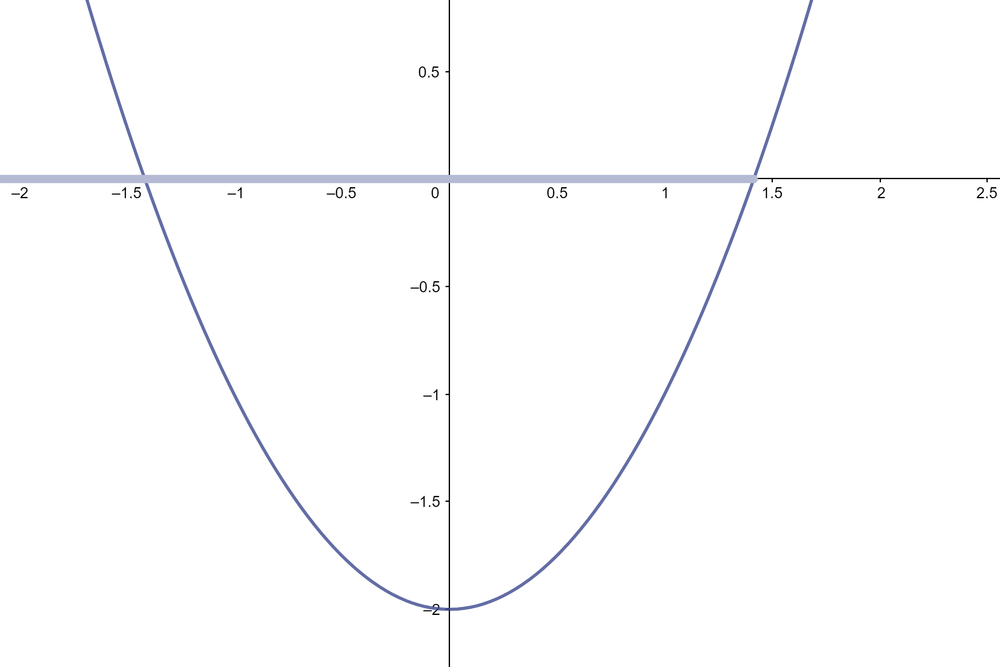
• האם ייתכן שהפרבולה [math]\displaystyle{ y=x^2-2 }[/math] עולה מהנקודה [math]\displaystyle{ (0,-2) }[/math] אל הנקודה [math]\displaystyle{ (2,2) }[/math] בלי לחתוך את ציר האיקס?

• כיוון שאין פתרון למשוואה זו בשדה הרציונאליים, אנחנו רוצים לבנות את שדה הממשיים.

• כיצד ניתן לתאר את נקודת החיתוך החיובית של הפרבולה [math]\displaystyle{ y=x^2-2 }[/math] עם ציר האיקס באמצעות המספרים הרציונאליים אם כך?

(נבנה באמצעות גאוגברה.)

• ובכן, ניתן לומר שציר המספרים מתחלק לשניים - לפני שורש שתיים ואחרי שורש שתיים.

• כלומר, אולי אנחנו יכולים לייצג את נקודת החיתוך על ידי אוסף הנקודות שקטנות ממנה [math]\displaystyle{ \left\{x\in\mathbb{Q}| x\lt 0 \vee x^2 \lt 2\right\} }[/math], זו הקרן באיור.

• הרעיון הזה של חיתוך ציר הרציונאליים סביב נקודה בלתי קיימת הוליד את חתכי דדקינד.

חתכי דדקינד

• הגדרה: חתך דדקינד הוא קבוצה [math]\displaystyle{ A\subseteq\mathbb{Q} }[/math] המקיימת:
  • [math]\displaystyle{ A\neq\emptyset }[/math]
  • [math]\displaystyle{ A }[/math] חסומה מלעיל.
  • לכל [math]\displaystyle{ m\in\mathbb{Q} }[/math] מתקיים כי [math]\displaystyle{ m\notin A }[/math] אם ורק אם [math]\displaystyle{ m }[/math] חסם מלעיל של [math]\displaystyle{ A }[/math]

• הערות ותזכורות:
  • חסם מלעיל של קבוצה הוא מספר שגדול יותר מכל איברי הקבוצה.
  • בחתך דדקינד אין מספר גדול ביותר, אחרת זה היה חסם מלעיל ששיך לקבוצה.
  • אם מספר שייך לחתך, בוודאי כל מספר נמוך ממנו שייך לחתך הרי לא ייתכן שמספר נמוך ממנו הוא חסם מלעיל.

• הקרן באיור לעיל היא חתך דדקינד שתפקידו להגדיר את שורש שתיים.
• כיצד ניתן להתייחס לקבוצות כאלה בתור מספרים?
• עלינו להגיד פעולות בין חתכי דדקינד ולהוכיח שמדובר בשדה.
• כאשר נגדיר את הפעולות, נזכור שמטרתינו היא להגדיר את הנקודות "החסרות" על הציר.

חיבור חתכי דדקינד

• יהיו שתי חתכים [math]\displaystyle{ A,B }[/math], נגדיר את החיבור:
  • [math]\displaystyle{ A+B=\left\{a+b|a\in A,b\in B\right\} }[/math]

• החיבור הוא חתך דדקינד בעצמו:
  • כיוון שA,B אינן ריקות גם A+B אינה ריקה.
  • סכום חסמי מלעיל של A וB חוסם את A+B.
  • יהי [math]\displaystyle{ a+b\in A+B }[/math], כיוון שאיברי החתכים אינם חסמי מלעיל, קיימים [math]\displaystyle{ a\lt c\in A }[/math] וכן [math]\displaystyle{ b\lt d\in B }[/math] ולכן [math]\displaystyle{ a+b\lt c+d\in A+B }[/math] ו[math]\displaystyle{ a+b }[/math] אינו חסם מלעיל של [math]\displaystyle{ A+B }[/math]
  • יהי [math]\displaystyle{ m\in\mathbb{Q} }[/math] שאינו חסם מלעיל של [math]\displaystyle{ A+B }[/math], לכן קיימים [math]\displaystyle{ m\lt a+b\in A+B }[/math]. כעת [math]\displaystyle{ m-a\lt b }[/math] כלומר [math]\displaystyle{ m-a }[/math] אינו חסם מלעיל של B ולכן שייך לקבוצה. סה"כ [math]\displaystyle{ m=a+(m-a)\in A+B }[/math].

חתך האפס

• נגדיר את חתך האפס, בהמשך נוכיח שהוא נייטרלי לחיבור.
• [math]\displaystyle{ 0_D=\left\{x\in\mathbb{Q}|x\lt 0\right\} }[/math]

נגדי

• יהי חתך A, נגדיר את הנגדי:
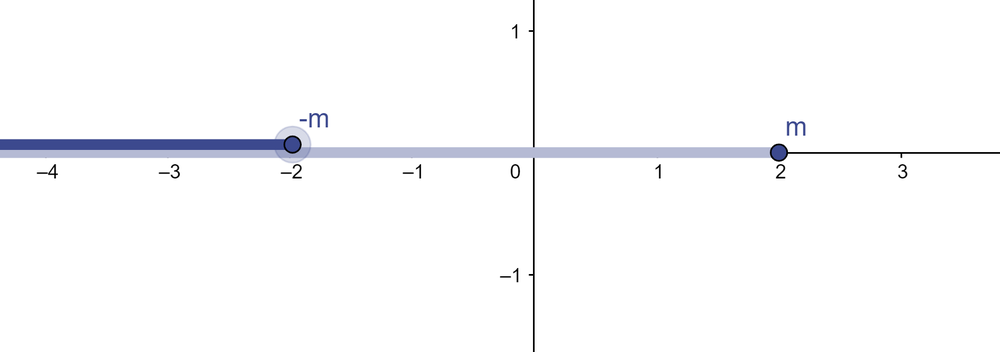
  • [math]\displaystyle{ -A=\left\{x\in\mathbb{Q}|\exists m\notin A:x\lt -m\right\} }[/math]

• לדוגמא [math]\displaystyle{ -\left\{x\in\mathbb{Q}|x\lt 2\right\}=\left\{x\in\mathbb{Q}|x\lt -2\right\} }[/math]

• הנגדי הוא חתך דדקינד בעצמו:
  • הנגדי לא ריק:
    • כיוון שA חסומה מלעיל יש לה חסם, וכל המספרים שקטנים ממינוס החסם שייכים לנגדי, ולכן [math]\displaystyle{ -A\neq\emptyset }[/math]
  • הנגדי חסום מלעיל:
    • יהי [math]\displaystyle{ a\in A }[/math] לכן לכל [math]\displaystyle{ m\notin A }[/math] מתקיים כי [math]\displaystyle{ a\lt m }[/math] ולכן [math]\displaystyle{ -m\lt -a }[/math]
    • לכל [math]\displaystyle{ x\in -A }[/math] קיים [math]\displaystyle{ m\notin A }[/math] כך ש [math]\displaystyle{ x\lt -m }[/math] ולכן [math]\displaystyle{ x\lt -a }[/math]
    • בעצם הנגדי של כל איבר בA הוא חסם מלעיל של [math]\displaystyle{ -A }[/math].
  • כל איבר בנגדי אינו חסם מלעיל:
    • לכל איבר בנגדי [math]\displaystyle{ x\lt -m }[/math] לכן אמצע הקטע בין [math]\displaystyle{ x,-m }[/math] גדול מ[math]\displaystyle{ x }[/math] וקטן מ[math]\displaystyle{ -m }[/math] ולכן שייך לנגדי [math]\displaystyle{ -A }[/math] ולכן [math]\displaystyle{ x }[/math] אינו חסם מלעיל.
  • אם איבר אינו חסם מלעיל, הוא שייך לנגדי:
    • נניח [math]\displaystyle{ y }[/math] אינו חסם מלעיל של [math]\displaystyle{ -A }[/math] לכן קיים [math]\displaystyle{ y\lt x\in -A }[/math] ולכן קיים [math]\displaystyle{ m\notin A }[/math] כך ש [math]\displaystyle{ y\lt x\lt -m }[/math] ולכן [math]\displaystyle{ y\in -A }[/math]

יחס סדר

• יחס ההכלה הוא יחס סדר לינארי (מלא) על קבוצת חתכי דדקינד
• הוכחה:
  • יהיו שני חתכים A,B.
  • אם קיים [math]\displaystyle{ m\notin A }[/math] חסם מלעיל של A כך ש[math]\displaystyle{ m\in B }[/math] אזי כל איבר של A אינו חסם מלעיל של B ולכן שייך לB, כלומר [math]\displaystyle{ A\subseteq B }[/math]
  • אחרת, לכל [math]\displaystyle{ m\notin A }[/math] מתקיים כי [math]\displaystyle{ m\notin B }[/math]. כלומר [math]\displaystyle{ \overline{A}\subseteq\overline{B} }[/math] ולכן [math]\displaystyle{ B\subseteq A }[/math]

• נגדיר את החתכים החיוביים להיות כל החתכים A כך ש[math]\displaystyle{ 0_D \lt A }[/math] ונגדיר את החתכים השליליים על ידי [math]\displaystyle{ 0_D \gt A }[/math]

• טענה: [math]\displaystyle{ A\geq 0_D }[/math] אם ורק אם [math]\displaystyle{ -A\leq 0_D }[/math]
• הוכחה:
  • ראשית נניח כי [math]\displaystyle{ A\geq 0_D }[/math]
    • כלומר בעצם [math]\displaystyle{ 0_D\subseteq A }[/math] ולכן לכל חסם מלעיל [math]\displaystyle{ m\notin A }[/math] מתקיים כי [math]\displaystyle{ 0\leq m }[/math].
    • לכן לכל [math]\displaystyle{ x\in -A }[/math] מתקיים כי [math]\displaystyle{ x\lt -m\lt 0 }[/math]
    • כלומר כל האיברים ב[math]\displaystyle{ -A }[/math] שליליים, ולכן [math]\displaystyle{ -A\subseteq 0_D }[/math] כלומר [math]\displaystyle{ -A\leq 0_D }[/math]
  • בכיוון ההפוך, נניח כי [math]\displaystyle{ -A\leq 0_D }[/math]
    • לכן כל האיברים ב[math]\displaystyle{ -A }[/math] שליליים.
    • אם קיים [math]\displaystyle{ 0\gt m\notin A }[/math] אזי [math]\displaystyle{ 0\lt -\frac{m}{2}\in -A }[/math] בסתירה.
  • לכן כל המספרים השליליים שייכים לA, כלומר [math]\displaystyle{ 0_D\subseteq A }[/math] ולכן [math]\displaystyle{ A\geq 0_D }[/math]

כפל חתכי דדקינד

• יהיו שני חתכי דדקינד אי שליליים [math]\displaystyle{ 0_D\leq A,B }[/math], נגדיר את הכפל:
  • [math]\displaystyle{ A\cdot B =\left\{x\in\mathbb{Q}:\forall m_A\notin A\forall m_B\notin B:x\lt m_A\cdot m_B\right\} }[/math]
• אם A שלילי, וB אי שלילי, נגדיר:
  • [math]\displaystyle{ A\cdot B = - (-A)\cdot B }[/math]
• אם A אי שלילי, וB שלילי, נגדיר:
  • [math]\displaystyle{ A\cdot B = - A\cdot (-B) }[/math]
• אם A,B שליליים נגדיר:
  • [math]\displaystyle{ A\cdot B = (-A)\cdot (-B) }[/math]

שדה הממשיים

הגדרת המספרים הממשיים

• הגדרה:
  • [math]\displaystyle{ \mathbb{R} }[/math] הוא קבוצת כל חתכי דדקינד.

• נוכיח שמדובר בשדה ביחס לפעולות החיבור והכפל שהגדרנו לעיל, ולאחר מכן נתאר את הייצוג העשרוני של המספרים הממשיים.