משתמש:אור שחף/133 - הרצאה/8.5.11: הבדלים בין גרסאות בדף
(יצירת דף עם התוכן "=התכנסות במידה שווה {{הערה|(המשך)}}= ==הערה== אם <math>f_n\to f</math> במ"ש על I אז לכל <math>x\in I</math> ברור שמת...") |
אין תקציר עריכה |
||
| שורה 1: | שורה 1: | ||
=התכנסות במידה שווה {{הערה|(המשך)}}= | =התכנסות במידה שווה {{הערה|(המשך)}}= | ||
'''תזכורת:''' תהי <math>\{f_n\}</math> סדרת פונקציות בקטע I כך שלכל <math>x\in I</math> קיים הגבול <math>f(x)=\lim_{n\to\infty} f_n(x)</math> (כלומר, הפונקציה הגבולית מוגדרת בכל I). הגדרנו ש-<math>f_n\to f</math> במידה שווה ב-I אם לכל <math>\varepsilon>0</math> קיים <math>n_0\in\mathbb N</math> כך שאם <math>n>n_0</math> אז <math>|f(x)-f_n(x)|<\varepsilon</math> לכל <math>x\in I</math>. | |||
==הערה== | ==הערה== | ||
אם <math>f_n\to f</math> במ"ש על I אז לכל <math>x\in I</math> ברור שמתקיים <math>f(x)=\lim_{n\to\infty} f_n(x)</math>, כלומר התכנסות במ"ש גוררת התכנסות נקודתית. ההיפך אינו נכון. | אם <math>f_n\to f</math> במ"ש על I אז לכל <math>x\in I</math> ברור שמתקיים <math>f(x)=\lim_{n\to\infty} f_n(x)</math>, כלומר התכנסות במ"ש גוררת התכנסות נקודתית. ההיפך אינו נכון. | ||
| שורה 8: | שורה 11: | ||
* <math>\lim_{n\to\infty}\sup_{x\in I}|f(x)-f_n(x)|<\varepsilon</math> | * <math>\lim_{n\to\infty}\sup_{x\in I}|f(x)-f_n(x)|<\varepsilon</math> | ||
===הוכחה=== | ===הוכחה=== | ||
ראשית נוכיח שהתנאי הראשון גורר את השני: אם נגדיר לכל n את <math>a_n=\sup_{x\in I}|f(x)-f_n(x)|</math> אז יש להוכיח כי <math>\lim_{n\to\infty} a_n=0</math>. אבל אם <math>\varepsilon>0</math> ידוע כי קיים <math>n_0\in\mathbb N</math> כך שלכל <math>n>n_0</math> מתקיים <math>|f(x)-f_n(x)|<\ | ראשית נוכיח שהתנאי הראשון גורר את השני: אם נגדיר לכל n את <math>a_n=\sup_{x\in I}|f(x)-f_n(x)|</math> אז יש להוכיח כי <math>\lim_{n\to\infty} a_n=0</math>. אבל אם <math>\varepsilon>0</math> ידוע כי קיים <math>n_0\in\mathbb N</math> כך שלכל <math>n>n_0</math> מתקיים <math>|f(x)-f_n(x)|<\frac\varepsilon2</math> לכל <math>x\in I</math>. נובע מיד שאם <math>n>n_0</math> אז <math>0\le a_n=\sup_{x\in I}|f(x)-f_n(x)|\le\frac\varepsilon2<\varepsilon</math> ולכן <math>\forall n>n_0:\ |a_n-0|<\varepsilon</math> והוכחנו <math>a_n\to0</math>, כדרוש. | ||
לצד השני יהי <math>\varepsilon>0</math> נתון. ידוע כי קיים <math>n_0\in\mathbb N</math> כך שלכל <math>n>n_0</math> מתקיים <math>\sup_{x\in I}|f(x)-f_n(x)|<\varepsilon</math> ולכן | לצד השני יהי <math>\varepsilon>0</math> נתון. ידוע כי קיים <math>n_0\in\mathbb N</math> כך שלכל <math>n>n_0</math> מתקיים <math>\sup_{x\in I}|f(x)-f_n(x)|<\varepsilon</math> ולכן <math>\forall n>n_0:\ |f(x)-f_n(x)|<\varepsilon</math> עבור <math>x\in I</math>. {{משל}} | ||
==דוגמה== | ==דוגמה== | ||
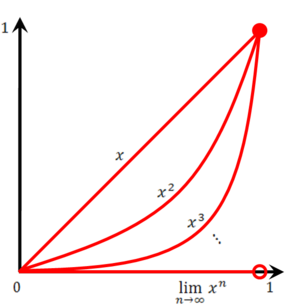
בקטע <math>[0,1)</math> ברור כי <math>\lim_{n\to\infty}x^n=0</math>. | [[קובץ:גרף חזקות שונות של x.png|ממוזער|300px|ימין]] | ||
בקטע <math>[0,1)</math> ברור כי <math>\lim_{n\to\infty}x^n=0</math>. | |||
נראה כי ההתכנסות נקודתית ולא במ"ש: <math>\forall n\in\mathbb N:\ a_n=\sup_{x\in[0,1)}|x^n-0|=1\ne0</math>. {{משל}} | |||
נעיר כי בקטע <math>[0,r]</math> עבור <math>r<1</math> דווקא '''יש''' התכנסות במ"ש: <math>\forall n\in\mathbb N:\ a_n=\sup_{x\in[0,r]}|x^n-0|=r^n</math> ולכן <math>\lim_{n\to\infty}a_n=\lim_{n\to\infty}r^n=0</math>, כדרוש. {{משל}} | |||
==משפט 2== | ==משפט 2== | ||
נניח ש-<math>\lim_{n\to\infty} f_n(x)=f(x)</math> במ"ש ב-I. עוד נניח שעבור איזה <math>x_0\in I</math> כל <math>f_n</math> רציפה ב-<math>x_0</math>. אזי גם f רציפה ב-<math>x_0</math>. | נניח ש-<math>\lim_{n\to\infty} f_n(x)=f(x)</math> במ"ש ב-I. עוד נניח שעבור איזה <math>x_0\in I</math> כל <math>f_n</math> רציפה ב-<math>x_0</math>. אזי גם f רציפה ב-<math>x_0</math>. | ||
===הוכחה=== | ===הוכחה=== | ||
יהי <math>\varepsilon>0</math> נתון. <math>f_n\to f</math> במ"ש ב-I קיים n טבעי מסויים כך שלכל <math>x\in I</math> מתקיים <math>|f(x)-f_n(x)|<\ | יהי <math>\varepsilon>0</math> נתון. <math>f_n\to f</math> במ"ש ב-I ולכן קיים n טבעי מסויים כך שלכל <math>x\in I</math> מתקיים <math>|f(x)-f_n(x)|<\frac\varepsilon3</math>. <math>f_n</math> רציפה ב-<math>x_0</math> ולכן קיים <math>\delta>0</math> כך שאם <math>|x-x_0|<\delta</math> אז <math>|f_n(x)-f_n(x_0)|<\frac\varepsilon3</math> נובע שאם <math>|x-x_0|<\delta</math> אז <math>|f(x)-f(x_0)|\le|f(x)-f_n(x)|+|f_n(x)-f_n(x_0)|+|f_n(x_0)-f(x_0)|<\frac\varepsilon3+\frac\varepsilon3+\frac\varepsilon3=\varepsilon</math>. {{משל}} | ||
===מסקנה=== | ===מסקנה=== | ||
בתנאים של משפט 2, אם כל <math>f_n</math> רציפה בקטע I כולו, אז גם f רציפה ב-I כולו. | בתנאים של משפט 2, אם כל <math>f_n</math> רציפה בקטע I כולו, אז גם f רציפה ב-I כולו. | ||
===דוגמה=== | |||
בקטע <math>[0,1]</math> ברור כי <math>\lim_{n\to\infty}=\begin{cases}0&0\le x<1\\1&x=1\end{cases}</math>. כאן כל <math>x^n</math> רציפה ב-<math>[0,1]</math> ואילו הפונקציה הגבולית לא רציפה. זה אינו סותר את משפט 2 כי כבר ראינו שההתכנסות אינה במ"ש. | בקטע <math>[0,1]</math> ברור כי <math>\lim_{n\to\infty}x^n=\begin{cases}0&0\le x<1\\1&x=1\end{cases}</math>. כאן כל <math>x^n</math> רציפה ב-<math>[0,1]</math> ואילו הפונקציה הגבולית לא רציפה. זה אינו סותר את משפט 2 כי כבר ראינו שההתכנסות אינה במ"ש. | ||
==משפט 3== | ==משפט 3== | ||
| שורה 29: | שורה 38: | ||
===הוכחה=== | ===הוכחה=== | ||
לא נוכיח שבתנאים הללו f אינטגרבילית (בד"כ זה יתקיים אוטומטית אם כל ה-<math>f_n</math> רציפות למקוטעין) | לא נוכיח שבתנאים הללו f אינטגרבילית (בד"כ זה יתקיים אוטומטית אם כל ה-<math>f_n</math> רציפות למקוטעין), ונסתפק בהוכחה לכך ש-<math>\int\limits_a^b f=\lim_{n\to\infty}\int\limits_a^b f_n</math>. שקול להוכיח ש-<math>\lim_{n\to\infty}\int\limits_a^b f-\int\limits_a^b f_n=0</math>. ובכן יהי <math>\varepsilon>0</math> נתון. כיוון ש-<math>f_n\to f</math> במ"ש על I <math>\exists n_0\in\mathbb N:\ \forall n>n_0:\ \sup_{x\in[a,b]}|f(x)-f_n(x)|<\frac\varepsilon{b-a}</math>. נובע שלכל <math>n>n_0</math> <math>\left|\int\limits_a^b(f-f_n)\right|\le\int\limits_a^b|f-f_n|\le(b-a)\sup_{x\in I}|f(x)-f_n(x)|<(b-a)\frac\varepsilon{b-a}=\varepsilon</math>. מכאן נובע ש-<math>\lim_{n\to\infty}\left|\int\limits_a^b (f-f_n)\right|=0</math>. {{משל}} | ||
===דוגמה=== | ===דוגמה=== | ||
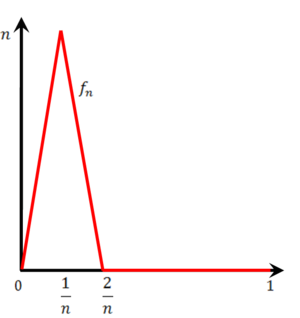
[[קובץ:פונקציה בין n ל-0.png|300px|ימין]] | |||
משמאל נתונה הפונקציה <math>f_n</math> עבור <math>n\in\mathbb N</math> כלשהו. | |||
נוכיח כי <math>\forall x\in[0,1]:\ \lim_{n\to\infty}f_n(x)=0</math>: עבור <math>x=0</math> לכל n <math>f_n(0)=0</math> ולכן <math>\lim_{n\to\infty} f_n(0)=0</math>. אם <math>x\in(0,1]</math> אז קיים <math>n_0\in\mathbb N</math> כך ש-<math>\frac2{n_0}<x</math> ולכן לכל <math>n>n_0</math> מתקיים <math>\frac2n<\frac2{n_0}<x</math>, מה שגורר כי <math>f_n(x)=0</math> לכל <math>n\in\mathbb N</math> ונובע ש-<math>\lim_{n\to\infty}f_n(x)=0</math>. בזה הוכחנו את הטענה ש-<math>0=\lim_{n\to\infty}f_n(x)</math> נקודתית ב-<math>[0,1]</math>. {{משל}} נעיר שההתכנסות "מאוד" לא במ"ש כי <math>\sup_{x\in[0,1]}|f_n(x)-0|=n\to\infty</math>. | |||
נוכיח כי <math>\lim_{n\to\infty}\int\limits_0^1 f_n\ne\int\limits_0^1 0\mathrm dx</math> (כאשר <math>f(x)=0</math> היא הפונקציה הגבולית): לכל n {{left|<math>\int\limits_0^1 f_n=</math> השטח מתחת לגרף <math>=\frac12\cdot n\cdot\frac2n=1\ne0</math>}} {{משל}} | |||
דוגמה נגדית: <math>f_n(x)=\frac{\sin\left(n^2x\right)}n</math> | השערה סבירה אבל מאוד לא נכונה: אם <math>f_n\to f</math> במ"ש ב-I אז <math>f_n'\to f'</math> ב-I. דוגמה נגדית: נגדיר <math>f_n(x)=\frac{\sin\left(n^2x\right)}n</math>. | ||
* נוכיח ש-<math>\lim_{n\to\infty} f_n(x)=0</math> במ"ש בכל <math>\mathbb R</math>: <math>\forall n\in\mathbb N:\ a_n=\sup_{x\in\mathbb R}\left|\frac{\sin\left(n^2x\right)}n-0\right|=\sup_{x\in\mathbb R}\frac{\left|\sin\left(n^2x\right)\right|}n=\frac1n\to0</math>. | |||
* נוכיח <math>f_n'\not\to0'=0</math>: לכל n ולכל <math>x\in\mathbb R</math> מתקיים <math>f_n'(x)=n\cos\left(n^2x\right)</math> ועבור <math>x\in\mathbb R</math> כלשהו <math>\lim_{n\to\infty}f_n'(x)=\lim_{n\to\infty} n\cos\left(n^2x\right)</math> שאינו קיים. {{משל}} | |||
==משפט 4== | ==משפט 4== | ||
תהי <math>\{f_n\}</math> סדרת פונקציות בעלות | תהי <math>\{f_n\}</math> סדרת פונקציות בעלות נגזרות רציפות <math>f_n'</math> בקטע <math>[a,b]</math>. נניח שהסדרה <math>\{f_n\}</math> מתכנסת בנקודה אחת (לפחות) <math>x_0\in[a,b]</math> והסדרה <math>\{f_n'\}</math> מתכנסת במ"ש ל-g ב-<math>[a,b]</math>. אזי <math>\lim_{n\to\infty} f_n(x)</math> קיים לכל <math>x\in[a,b]</math> ומגדיר פונקציה גבולית f שהיא גזירה ב-<math>[a,b]</math>. יתר על כן <math>\forall x\in[a,b]:\ f'(x)=g(x)</math>. | ||
===הוכחה=== | ===הוכחה=== | ||
נקח <math>x\in[a,b]</math> כלשהי. לכל n הפונקציה <math>f_n'</math> רציפה (נתון) ונוכל להפעיל את המשפט היסודי לומר <math>f_n(x)-f_n(x_0)=\int\limits_{x_0}^x f_n'</math>. נעביר אגף: <math>f_n(x)=f_n(x_0)+\int\limits_{x_0}^x f_n'</math>. כעת נתון שקיים <math>\lim_{n\to\infty} f_n( | נקח <math>x\in[a,b]</math> כלשהי. לכל n הפונקציה <math>f_n'</math> רציפה (נתון) ונוכל להפעיל את המשפט היסודי לומר <math>f_n(x)-f_n(x_0)=\int\limits_{x_0}^x f_n'</math>. נעביר אגף: <math>f_n(x)=f_n(x_0)+\int\limits_{x_0}^x f_n'</math>. כעת נתון שקיים <math>\lim_{n\to\infty} f_n(x_0)</math>, נקרא לו <math>\alpha</math>. יתר על כן נתון ש-<math>\lim_{n\to\infty} f_n'(t)=g(t)</math> במ"ש ב-<math>[a,b]</math> וכל שכן <math>\lim_{n\to\infty}f_n'(t)=g(t)</math> במ"ש בתת הקטע בין <math>x_0</math> ל-x. נסיק ממשפט 3 ש-<math>\lim_{n\to\infty}\int\limits_{x_0}^x f_n'=\int\limits_{x_0}^x g</math> נובע שלכל <math>x\in[a,b]</math> קיים <math>f(x)=\lim_{n\to\infty} f_n(x)=\lim_{n\to\infty}\left(f_n(x_0)+\int\limits_{x_0}^x f_n'\right)=\alpha+\int\limits_{x_0}^x g</math> והוכחנו את קיום הפונקציה הגבולית f. נותר להוכיח שהיא גזירה וש-<math>\forall x\in[a,b]:\ f'(x)=g(x)</math>. לפי הנתון כל <math>f_n'</math> רציפה ו-<math>g(t)=\lim_{n\to\infty} f_n'(t)</math> במ"ש על <math>[a,b]</math>. לכן משפט 2 נותן ש-<math>g</math> רציפה ב-<math>[a,b]</math> וכיוון שלכל <math>x\in[a,b]</math> מתקיים <math>f(x)=\alpha+\int\limits_{x_0}^x g</math> החלק הראשון של המשפט היסודי נותן <math>f'=g</math> לכל <math>x\in[a,b]</math>. {{משל}} | ||
גרסה מ־19:23, 9 במאי 2011
התכנסות במידה שווה (המשך)
תזכורת: תהי [math]\displaystyle{ \{f_n\} }[/math] סדרת פונקציות בקטע I כך שלכל [math]\displaystyle{ x\in I }[/math] קיים הגבול [math]\displaystyle{ f(x)=\lim_{n\to\infty} f_n(x) }[/math] (כלומר, הפונקציה הגבולית מוגדרת בכל I). הגדרנו ש-[math]\displaystyle{ f_n\to f }[/math] במידה שווה ב-I אם לכל [math]\displaystyle{ \varepsilon\gt 0 }[/math] קיים [math]\displaystyle{ n_0\in\mathbb N }[/math] כך שאם [math]\displaystyle{ n\gt n_0 }[/math] אז [math]\displaystyle{ |f(x)-f_n(x)|\lt \varepsilon }[/math] לכל [math]\displaystyle{ x\in I }[/math].
הערה
אם [math]\displaystyle{ f_n\to f }[/math] במ"ש על I אז לכל [math]\displaystyle{ x\in I }[/math] ברור שמתקיים [math]\displaystyle{ f(x)=\lim_{n\to\infty} f_n(x) }[/math], כלומר התכנסות במ"ש גוררת התכנסות נקודתית. ההיפך אינו נכון.
משפט 1
יהיו קבוצת הפונקציות [math]\displaystyle{ \{f_n\} }[/math] והפונקציה f מוגדרות בקטע I. אז התנאים הבאים שקולים:
- [math]\displaystyle{ f(x)=\lim_{n\to\infty} f_n(x) }[/math] במ"ש ב-I
- [math]\displaystyle{ \lim_{n\to\infty}\sup_{x\in I}|f(x)-f_n(x)|\lt \varepsilon }[/math]
הוכחה
ראשית נוכיח שהתנאי הראשון גורר את השני: אם נגדיר לכל n את [math]\displaystyle{ a_n=\sup_{x\in I}|f(x)-f_n(x)| }[/math] אז יש להוכיח כי [math]\displaystyle{ \lim_{n\to\infty} a_n=0 }[/math]. אבל אם [math]\displaystyle{ \varepsilon\gt 0 }[/math] ידוע כי קיים [math]\displaystyle{ n_0\in\mathbb N }[/math] כך שלכל [math]\displaystyle{ n\gt n_0 }[/math] מתקיים [math]\displaystyle{ |f(x)-f_n(x)|\lt \frac\varepsilon2 }[/math] לכל [math]\displaystyle{ x\in I }[/math]. נובע מיד שאם [math]\displaystyle{ n\gt n_0 }[/math] אז [math]\displaystyle{ 0\le a_n=\sup_{x\in I}|f(x)-f_n(x)|\le\frac\varepsilon2\lt \varepsilon }[/math] ולכן [math]\displaystyle{ \forall n\gt n_0:\ |a_n-0|\lt \varepsilon }[/math] והוכחנו [math]\displaystyle{ a_n\to0 }[/math], כדרוש.
לצד השני יהי [math]\displaystyle{ \varepsilon\gt 0 }[/math] נתון. ידוע כי קיים [math]\displaystyle{ n_0\in\mathbb N }[/math] כך שלכל [math]\displaystyle{ n\gt n_0 }[/math] מתקיים [math]\displaystyle{ \sup_{x\in I}|f(x)-f_n(x)|\lt \varepsilon }[/math] ולכן [math]\displaystyle{ \forall n\gt n_0:\ |f(x)-f_n(x)|\lt \varepsilon }[/math] עבור [math]\displaystyle{ x\in I }[/math]. [math]\displaystyle{ \blacksquare }[/math]
דוגמה
בקטע [math]\displaystyle{ [0,1) }[/math] ברור כי [math]\displaystyle{ \lim_{n\to\infty}x^n=0 }[/math].
נראה כי ההתכנסות נקודתית ולא במ"ש: [math]\displaystyle{ \forall n\in\mathbb N:\ a_n=\sup_{x\in[0,1)}|x^n-0|=1\ne0 }[/math]. [math]\displaystyle{ \blacksquare }[/math]
נעיר כי בקטע [math]\displaystyle{ [0,r] }[/math] עבור [math]\displaystyle{ r\lt 1 }[/math] דווקא יש התכנסות במ"ש: [math]\displaystyle{ \forall n\in\mathbb N:\ a_n=\sup_{x\in[0,r]}|x^n-0|=r^n }[/math] ולכן [math]\displaystyle{ \lim_{n\to\infty}a_n=\lim_{n\to\infty}r^n=0 }[/math], כדרוש. [math]\displaystyle{ \blacksquare }[/math]
משפט 2
נניח ש-[math]\displaystyle{ \lim_{n\to\infty} f_n(x)=f(x) }[/math] במ"ש ב-I. עוד נניח שעבור איזה [math]\displaystyle{ x_0\in I }[/math] כל [math]\displaystyle{ f_n }[/math] רציפה ב-[math]\displaystyle{ x_0 }[/math]. אזי גם f רציפה ב-[math]\displaystyle{ x_0 }[/math].
הוכחה
יהי [math]\displaystyle{ \varepsilon\gt 0 }[/math] נתון. [math]\displaystyle{ f_n\to f }[/math] במ"ש ב-I ולכן קיים n טבעי מסויים כך שלכל [math]\displaystyle{ x\in I }[/math] מתקיים [math]\displaystyle{ |f(x)-f_n(x)|\lt \frac\varepsilon3 }[/math]. [math]\displaystyle{ f_n }[/math] רציפה ב-[math]\displaystyle{ x_0 }[/math] ולכן קיים [math]\displaystyle{ \delta\gt 0 }[/math] כך שאם [math]\displaystyle{ |x-x_0|\lt \delta }[/math] אז [math]\displaystyle{ |f_n(x)-f_n(x_0)|\lt \frac\varepsilon3 }[/math] נובע שאם [math]\displaystyle{ |x-x_0|\lt \delta }[/math] אז [math]\displaystyle{ |f(x)-f(x_0)|\le|f(x)-f_n(x)|+|f_n(x)-f_n(x_0)|+|f_n(x_0)-f(x_0)|\lt \frac\varepsilon3+\frac\varepsilon3+\frac\varepsilon3=\varepsilon }[/math]. [math]\displaystyle{ \blacksquare }[/math]
מסקנה
בתנאים של משפט 2, אם כל [math]\displaystyle{ f_n }[/math] רציפה בקטע I כולו, אז גם f רציפה ב-I כולו.
דוגמה
בקטע [math]\displaystyle{ [0,1] }[/math] ברור כי [math]\displaystyle{ \lim_{n\to\infty}x^n=\begin{cases}0&0\le x\lt 1\\1&x=1\end{cases} }[/math]. כאן כל [math]\displaystyle{ x^n }[/math] רציפה ב-[math]\displaystyle{ [0,1] }[/math] ואילו הפונקציה הגבולית לא רציפה. זה אינו סותר את משפט 2 כי כבר ראינו שההתכנסות אינה במ"ש.
משפט 3
נניח שלכל n [math]\displaystyle{ f_n }[/math] מוגדרת ואינטגרבילית ב-[math]\displaystyle{ I=[a,b] }[/math] ונניח שקיים [math]\displaystyle{ f(x)=\lim_{n\to\infty}f_n(x) }[/math] במ"ש ב-I. אזי f אינטגרבילית ב-I ומתקיים [math]\displaystyle{ \int\limits_a^b f=\lim_{n\to\infty}\int\limits_a^b f_n }[/math].
הוכחה
לא נוכיח שבתנאים הללו f אינטגרבילית (בד"כ זה יתקיים אוטומטית אם כל ה-[math]\displaystyle{ f_n }[/math] רציפות למקוטעין), ונסתפק בהוכחה לכך ש-[math]\displaystyle{ \int\limits_a^b f=\lim_{n\to\infty}\int\limits_a^b f_n }[/math]. שקול להוכיח ש-[math]\displaystyle{ \lim_{n\to\infty}\int\limits_a^b f-\int\limits_a^b f_n=0 }[/math]. ובכן יהי [math]\displaystyle{ \varepsilon\gt 0 }[/math] נתון. כיוון ש-[math]\displaystyle{ f_n\to f }[/math] במ"ש על I [math]\displaystyle{ \exists n_0\in\mathbb N:\ \forall n\gt n_0:\ \sup_{x\in[a,b]}|f(x)-f_n(x)|\lt \frac\varepsilon{b-a} }[/math]. נובע שלכל [math]\displaystyle{ n\gt n_0 }[/math] [math]\displaystyle{ \left|\int\limits_a^b(f-f_n)\right|\le\int\limits_a^b|f-f_n|\le(b-a)\sup_{x\in I}|f(x)-f_n(x)|\lt (b-a)\frac\varepsilon{b-a}=\varepsilon }[/math]. מכאן נובע ש-[math]\displaystyle{ \lim_{n\to\infty}\left|\int\limits_a^b (f-f_n)\right|=0 }[/math]. [math]\displaystyle{ \blacksquare }[/math]
דוגמה
משמאל נתונה הפונקציה [math]\displaystyle{ f_n }[/math] עבור [math]\displaystyle{ n\in\mathbb N }[/math] כלשהו.
נוכיח כי [math]\displaystyle{ \forall x\in[0,1]:\ \lim_{n\to\infty}f_n(x)=0 }[/math]: עבור [math]\displaystyle{ x=0 }[/math] לכל n [math]\displaystyle{ f_n(0)=0 }[/math] ולכן [math]\displaystyle{ \lim_{n\to\infty} f_n(0)=0 }[/math]. אם [math]\displaystyle{ x\in(0,1] }[/math] אז קיים [math]\displaystyle{ n_0\in\mathbb N }[/math] כך ש-[math]\displaystyle{ \frac2{n_0}\lt x }[/math] ולכן לכל [math]\displaystyle{ n\gt n_0 }[/math] מתקיים [math]\displaystyle{ \frac2n\lt \frac2{n_0}\lt x }[/math], מה שגורר כי [math]\displaystyle{ f_n(x)=0 }[/math] לכל [math]\displaystyle{ n\in\mathbb N }[/math] ונובע ש-[math]\displaystyle{ \lim_{n\to\infty}f_n(x)=0 }[/math]. בזה הוכחנו את הטענה ש-[math]\displaystyle{ 0=\lim_{n\to\infty}f_n(x) }[/math] נקודתית ב-[math]\displaystyle{ [0,1] }[/math]. [math]\displaystyle{ \blacksquare }[/math] נעיר שההתכנסות "מאוד" לא במ"ש כי [math]\displaystyle{ \sup_{x\in[0,1]}|f_n(x)-0|=n\to\infty }[/math].
נוכיח כי [math]\displaystyle{ \lim_{n\to\infty}\int\limits_0^1 f_n\ne\int\limits_0^1 0\mathrm dx }[/math] (כאשר [math]\displaystyle{ f(x)=0 }[/math] היא הפונקציה הגבולית): לכל n
[math]\displaystyle{ \blacksquare }[/math]
השערה סבירה אבל מאוד לא נכונה: אם [math]\displaystyle{ f_n\to f }[/math] במ"ש ב-I אז [math]\displaystyle{ f_n'\to f' }[/math] ב-I. דוגמה נגדית: נגדיר [math]\displaystyle{ f_n(x)=\frac{\sin\left(n^2x\right)}n }[/math].
- נוכיח ש-[math]\displaystyle{ \lim_{n\to\infty} f_n(x)=0 }[/math] במ"ש בכל [math]\displaystyle{ \mathbb R }[/math]: [math]\displaystyle{ \forall n\in\mathbb N:\ a_n=\sup_{x\in\mathbb R}\left|\frac{\sin\left(n^2x\right)}n-0\right|=\sup_{x\in\mathbb R}\frac{\left|\sin\left(n^2x\right)\right|}n=\frac1n\to0 }[/math].
- נוכיח [math]\displaystyle{ f_n'\not\to0'=0 }[/math]: לכל n ולכל [math]\displaystyle{ x\in\mathbb R }[/math] מתקיים [math]\displaystyle{ f_n'(x)=n\cos\left(n^2x\right) }[/math] ועבור [math]\displaystyle{ x\in\mathbb R }[/math] כלשהו [math]\displaystyle{ \lim_{n\to\infty}f_n'(x)=\lim_{n\to\infty} n\cos\left(n^2x\right) }[/math] שאינו קיים. [math]\displaystyle{ \blacksquare }[/math]
משפט 4
תהי [math]\displaystyle{ \{f_n\} }[/math] סדרת פונקציות בעלות נגזרות רציפות [math]\displaystyle{ f_n' }[/math] בקטע [math]\displaystyle{ [a,b] }[/math]. נניח שהסדרה [math]\displaystyle{ \{f_n\} }[/math] מתכנסת בנקודה אחת (לפחות) [math]\displaystyle{ x_0\in[a,b] }[/math] והסדרה [math]\displaystyle{ \{f_n'\} }[/math] מתכנסת במ"ש ל-g ב-[math]\displaystyle{ [a,b] }[/math]. אזי [math]\displaystyle{ \lim_{n\to\infty} f_n(x) }[/math] קיים לכל [math]\displaystyle{ x\in[a,b] }[/math] ומגדיר פונקציה גבולית f שהיא גזירה ב-[math]\displaystyle{ [a,b] }[/math]. יתר על כן [math]\displaystyle{ \forall x\in[a,b]:\ f'(x)=g(x) }[/math].
הוכחה
נקח [math]\displaystyle{ x\in[a,b] }[/math] כלשהי. לכל n הפונקציה [math]\displaystyle{ f_n' }[/math] רציפה (נתון) ונוכל להפעיל את המשפט היסודי לומר [math]\displaystyle{ f_n(x)-f_n(x_0)=\int\limits_{x_0}^x f_n' }[/math]. נעביר אגף: [math]\displaystyle{ f_n(x)=f_n(x_0)+\int\limits_{x_0}^x f_n' }[/math]. כעת נתון שקיים [math]\displaystyle{ \lim_{n\to\infty} f_n(x_0) }[/math], נקרא לו [math]\displaystyle{ \alpha }[/math]. יתר על כן נתון ש-[math]\displaystyle{ \lim_{n\to\infty} f_n'(t)=g(t) }[/math] במ"ש ב-[math]\displaystyle{ [a,b] }[/math] וכל שכן [math]\displaystyle{ \lim_{n\to\infty}f_n'(t)=g(t) }[/math] במ"ש בתת הקטע בין [math]\displaystyle{ x_0 }[/math] ל-x. נסיק ממשפט 3 ש-[math]\displaystyle{ \lim_{n\to\infty}\int\limits_{x_0}^x f_n'=\int\limits_{x_0}^x g }[/math] נובע שלכל [math]\displaystyle{ x\in[a,b] }[/math] קיים [math]\displaystyle{ f(x)=\lim_{n\to\infty} f_n(x)=\lim_{n\to\infty}\left(f_n(x_0)+\int\limits_{x_0}^x f_n'\right)=\alpha+\int\limits_{x_0}^x g }[/math] והוכחנו את קיום הפונקציה הגבולית f. נותר להוכיח שהיא גזירה וש-[math]\displaystyle{ \forall x\in[a,b]:\ f'(x)=g(x) }[/math]. לפי הנתון כל [math]\displaystyle{ f_n' }[/math] רציפה ו-[math]\displaystyle{ g(t)=\lim_{n\to\infty} f_n'(t) }[/math] במ"ש על [math]\displaystyle{ [a,b] }[/math]. לכן משפט 2 נותן ש-[math]\displaystyle{ g }[/math] רציפה ב-[math]\displaystyle{ [a,b] }[/math] וכיוון שלכל [math]\displaystyle{ x\in[a,b] }[/math] מתקיים [math]\displaystyle{ f(x)=\alpha+\int\limits_{x_0}^x g }[/math] החלק הראשון של המשפט היסודי נותן [math]\displaystyle{ f'=g }[/math] לכל [math]\displaystyle{ x\in[a,b] }[/math]. [math]\displaystyle{ \blacksquare }[/math]