חדוא 1 - ארז שיינר

88-132 חשבון אינפיניטיסימלי 1

סרטוני ותקציר ההרצאות

פרק 1 - מספרים וחסמים

קבוצות מספרים

• הטבעיים $\mathbb{N}=\{1,2,3,...\}$
• השלמים $\mathbb{Z}=\{0,-1,1,-2,2,...\}$
• הרציונאליים $\mathbb{Q}=\{\frac{p}{n}|p\in \mathbb{Z},n\in \mathbb{N}\}$
• הממשיים $\mathbb{R}$, כל השברים העשרוניים כולל האינסופיים

• חזקות ולוגריתמים

• העשרה: בנייה של שדה הממשיים באמצעות חתכי דדקינד

• לא קיים $x\in \mathbb{Q}$ כך ש $x^2=2$.
• במילים פשוטות, $\sqrt{2}$ אינו רציונאלי (בהמשך נוכיח שיש מספר ממשי כזה).

חסמים

• תהי $A\subseteq \mathbb{R}$ אזי:
  • $M\in \mathbb{A}$ נקרא המקסימום של A או האיבר הגדול ביותר של A אם לכל $a\in A$ מתקיים כי $a\le M$
  • $M\in \mathbb{R}$ נקרא חסם מלעיל של A אם לכל $a\in A$ מתקיים כי $a\le M$
  • $m\in \mathbb{A}$ נקרא המינימום של A או האיבר הקטן ביותר של A אם לכל $a\in A$ מתקיים כי $a\ge M$
  • $m\in \mathbb{R}$ נקרא חסם מלרע של A אם לכל $a\in A$ מתקיים כי $a\ge M$

• כמו כן:
  • אם יש איבר קטן ביותר בקבוצת חסמי המלעיל של A הוא נקרא החסם העליון של A, או הסופרמום של A ומסומן $sup(A)$
  • אם יש איבר גדול ביותר בקבוצת חסמי המלרע של A הוא נקרא החסם התחתון של A, או האינפימום של A ומסומן $inf(A)$

• בשדה הממשיים לכל קבוצה לא ריקה וחסומה מלעיל יש חסם עליון, ולכל קבוצה לא ריקה וחסומה מלרע יש חסם תחתון.
• בשדה הרציונאליים זה לא נכון; לקבוצה $A=\{x\in \mathbb{Q}|x^2<2\}$ אין מספר רציונאלי קטן ביותר מבין חסמי המלעיל שלה.

• תהי $A\subseteq \mathbb{R}$ ויהי $M\in \mathbb{R}$ אזי:
  • M הוא החסם העליון של A אם ורק אם M הוא חסם מלעיל של A ולכל מספר $M-\epsilon <M$ קיים מספר $a\in A$ כך ש $a>M-\epsilon$
  • m הוא החסם התחתון של A אם ורק אם m הוא חסם מלרע של A ולכל מספר $m<m+\epsilon$ קיים מספר $a\in A$ כך ש $a<m+\epsilon$

• דוגמא: תהיינה $\mathrm{\varnothing }\ne A,B\subseteq \mathbb{R}$ חסומות מלעיל כך שA אינה מכילה חסמי מלעיל של B, אזי $sup(A)\le sup(B)$

פרק 2 - סדרות

הגדרת הגבול

• הגדרת הגבול של סדרה:
• תהי סדרה ממשית $a_n$ ויהי מספר ממשי $L\in \mathbb{R}$.
• $L$ הינו גבול הסדרה $a_n$ (מסומן $lim{a}_n=L$ או $a_n\to L$) אם:
  • לכל סביבה של הגבול, קיים מקום בסדרה שאחריו כל איברי הסדרה נמצאים בסביבה הנתונה, כלומר:
  • לכל מרחק $\epsilon >0$ קיים מקום $N\in \mathbb{N}$ כך שאחריו לכל $n>N$ מתקיים כי $|a_n-L|<\epsilon$

• נגדיר ש$a_n\to \mathrm{\infty }$ אם לכל $M>0$ קיים $N\in \mathbb{N}$ כך שלכל $n>N$ מתקיים כי $a_n>M$
• נגדיר ש$a_n\to -\mathrm{\infty }$ אם $-a_n\to \mathrm{\infty }$

• טענה: תהי $a_n\to \mathrm{\infty }$ אזי $\frac{1}{a_n}\to 0$
• טענה: תהי $0\ne a_n\to 0$ אזי $\frac{1}{|a_n|}\to \mathrm{\infty }$

• הגבול הוא יחיד
• מספר סופי של איברים לא משפיע על הגבול
• סדרה מתכנסת במובן הצר חסומה

מבוא לחשבון גבולות (אריתמטיקה של גבולות)

• (אי שיוויון המשולש.)
• סכום.
• מכפלה.
• חלוקה.

כלים לחישוב גבולות

• סנדביץ' וחצי סדנביץ'
• $a_n\to 0⟺|a_n|\to 0$
• חסומה כפול אפיסה היא אפיסה.
• מבחן המנה (הוכחה בסיכום הבא על אי-שוויון הממוצעים).
  • תהי סדרה $a_n$ המקיימת כי גבול המנה הוא $\left|\frac{a_{n+1}}{a_n}\right|\to L$ אזי:
    • אם $1<L\le \mathrm{\infty }$ מתקיים כי $|a_n|\to \mathrm{\infty }$
    • אם $0\le L<1$ מתקיים כי $a_n\to 0$
    • מתקיים כי $\sqrt[n]{|a_n|}\to L$

• דוגמא:
  • $\sqrt[n]{n}\to 1$

• אינדוקציה.
• ברנולי - אקספוננט חיובי שואף לאפס, אחד או אינסוף.

חשבון גבולות (אריתמטיקה של גבולות)

• אריתמטיקה מורחבת (הכתיב הוא מקוצר ואינו מדוייק):
  • חסומה כפול אפיסה = אפיסה
  • חסומה חלקי אינסוף = אפיסה
  • $\mathrm{\infty }+\mathrm{\infty }=\mathrm{\infty }$
  • $\mathrm{\infty }\cdot \mathrm{\infty }=\mathrm{\infty }$
  • ${\mathrm{\infty }}^{\mathrm{\infty }}=\mathrm{\infty }$
  • $\frac{1}{0}\ne \mathrm{\infty }$
  • $\frac{1}{0^{+}}=\mathrm{\infty }$
  • $0^{\mathrm{\infty }}=0$
  • אינסוף כפול סדרה השואפת למספר חיובי = אינסוף.
  • אינסוף כפול סדרההשואפת למספר שלילי = אינסוף.
  • יש גבול סופי + אין גבול סופי = אין גבול סופי.
  • אינסוף ועוד חסומה שווה אינסוף.
  • אם $a>1$ אזי $a^{\mathrm{\infty }}=\mathrm{\infty }$
  • חזקת סדרות שואפת לחזקת הגבולות.

המקרים הבעייתיים

• המקרים הבעייתיים בהם צריך להפעיל מניפולציות אלגבריות או משפטים על מנת לחשב את הגבול:
  • $\frac{0}{0},\frac{\mathrm{\infty }}{\mathrm{\infty }},0\cdot \mathrm{\infty },\mathrm{\infty }-\mathrm{\infty },0^0,{\mathrm{\infty }}^0,1^{\mathrm{\infty }}$

סדרות מונוטוניות והמספר e

• כל סדרה מונוטונית הינה חסומה מתכנסת לגבול סופי, או שאינה חסומה ושואפת לגבול אינסופי.
• המספר e (הוכחות בעזרת אי-שוויון הממוצעים).
• $2<e<4$.
• אם $a_n\to \mathrm{\infty }$ אזי ${(1+\frac{1}{a_n})}^{a_n}\to e$
  • $[a_n]\le a_n\le [a_n]+1$, כאשר $[a_n]$ הוא המספר השלם הגדול ביותר שקטן או שווה ל$a_n$.
  • ${(1+\frac{1}{[a_n]+1})}^{[a_n]}\le {(1+\frac{1}{a_n})}^{a_n}\le {(1+\frac{1}{[a_n]})}^{[a_n]+1}$
  • שני הצדדים שואפים לe ולכן לפי כלל הסנדוויץ הסדרה אכן שואפת לe.
• אם $a_n\to -\mathrm{\infty }$ אזי ${(1+\frac{1}{a_n})}^{a_n}\to e$
  • ראשית ${(1-\frac{1}{n})}^n\to \frac{1}{e}$ (הוכחה בקישור לערך על המספר e).
  • כעת חזקה שלילית הופכת את השבר, וניתן לסיים את ההוכחה באופן דומה להוכחה במקרה הקודם.

• אם $a_n\to 1$ אזי $a_n^{b_n}\to e^{lim{b}_n\cdot (a_n-1)}$
  • $a_n^{b_n}={\left[{(1+(a_n-1))}^{\frac{1}{a_n-1}}\right]}^{b_n\cdot (a_n-1)}$.
  • ${(1+(a_n-1))}^{\frac{1}{a_n-1}}\to e$ בין אם $a_n-1$ שלילי או חיובי, לפי הטענות לעיל.
  • שימו לב שאם $a_n=1$, אז ממילא מקבלים 1 בנוסחא הסופית, ואז לא צריך לחלק ב$a_n-1$ ששווה אפס.

• דוגמא:
  • $lim{\left(\frac{n+1}{n-2}\right)}^n=e^{limn\cdot (\frac{n+1}{n-2}-1)}=e^{lim\frac{3n}{n-2}}=e^3$

פרק 4 - פונקציות ורציפות

מבוא לגבולות

• מבוא לגבולות (שיטות אלגבריות: כפל בצמוד, הוצאת חזקה משמעותית).
  • $\underset{x\to 2}{lim}\frac{x^2-4}{x-2}$
  • $\underset{x\to \mathrm{\infty }}{lim}\frac{2x^2+5x+3}{3x^2-100}$
  • $\underset{x\to \mathrm{\infty }}{lim}\sqrt{x^2+1}-x$
  • $\underset{x\to \mathrm{\infty }}{lim}\sqrt{x^2+x+1}-x$
  • $\underset{x\to \mathrm{\infty }}{lim}{x}^2-x$

הגדרת הגבול לפי היינה

• מרבית כללי האריתמטיקה המורחבות נובעים "בחינם" עבור פונקציות

הפונקציות הטריגונומטריות

• הגדרת סינוס וקוסינוס ע"י מעגל היחידה.
  • $si{n}^2(x)+co{s}^2(x)=1$
  • $sin(-x)=-sin(x),cos(-x)=cos(x)$
  • $sin(a+b)=sin(a)cos(b)+sin(b)cos(a),cos(a+b)=cos(a)cos(b)-sin(a)sin(b)$
  • $sin(2x)=2sin(x)cos(x),cos(2x)=co{s}^2(x)-si{n}^2(x)$

• 
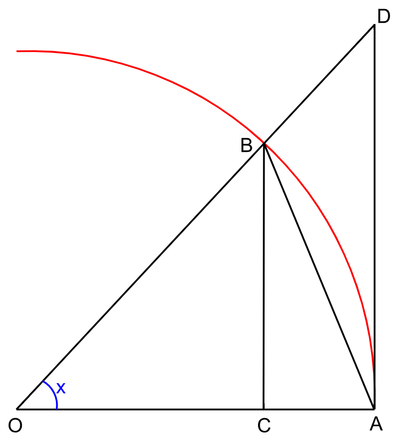
  • עבור זוית $0<x<\frac{\pi }{2}$ שטח המשולש חסום בשטח הגזרה (משולש פיצה עם הקשה) שחסום בשטח המשולש:
  • $S_{\mathrm{△}AOB}<S_{◯AOB}<S_{\mathrm{△}AOD}$
  • $\frac{sin(x)}{2}<\frac{x}{2}<\frac{tan(x)}{2}$
    • כיוון ש$0<sin(x)<x$ בתחום $(0,\frac{\pi }{2})$, נובע לפי סנדוויץ' ש$\underset{x\to 0^{+}}{lim}sin(x)=0$.
    • כיוון שמדובר בפונקציה אי זוגית, נובע שזה גם הגבול משני הצדדים.
    • כעת בתחום $(-\frac{\pi }{2},\frac{\pi }{2})$ הקוסינוס חיובית ולכן $cos(x)=\sqrt{1-si{n}^2(x)}$ ונובע כי $\underset{x\to 0}{lim}cos(x)=1$.
  • נחלק את אי השיוויון הטריגונומטרי בסינוס ונקבל:
  • $1<\frac{x}{sin(x)}<\frac{1}{cos(x)}$
  • לפי כלל הסנדביץ $\underset{x\to 0^{+}}{lim}\frac{sin(x)}{x}=1$
  • כיוון שמדובר בפונקציה זוגית, נובע שהגבול משני הצדדים שווה 1.

• ראינו ש$\underset{x\to 0}{lim}\frac{sin(x)}{x}=1$.
• שימו לב ש$\underset{x\to \mathrm{\infty }}{lim}\frac{sin(x)}{x}=0$, כיוון שמדובר בחסומה חלקי שואפת לאינסוף.

רציפות

• גבול של הרכבת פונקציות נכשל ללא רציפות.
  • $f(x)=\frac{x}{x},g(x)=0$ מתקיים כי $\underset{x\to 0}{lim}f(x)=1,\underset{x\to 2}{lim}g(x)=0$ אבל $\underset{x\to 2}{lim}f(g(x))\ne 1$.

• רציפות.
• הגדרה:
• פונקציה f נקראית רציפה בקטע $[a,b]$ אם f רציפה בכל נקודה בקטע $(a,b)$ ובנוסף $\underset{x\to a^{+}}{lim}f(x)=f(a)$ וגם $\underset{x\to b^{-}}{lim}f(x)=f(b)$

• טענה: אם f רציפה ב$x_0$ אזי לכל סדרה $x_n\to x_0$ (גם אם אינה שונה מ$x_0$) מתקיים כי $f(x_n)\to f(x_0)$.
• הרכבת רציפות: תהי f רציפה ב$x_0$ ותהי g רציפה ב$f(x_0)$. אזי $g\circ f$ רציפה ב$x_0$.
  • הוכחה:
  • תהי סדרה $x_0\ne x_n\to x_0$ אזי $f(x_n)\to f(x_0)$
  • לפי הטענה הקודמת, $g(f(x_n))\to g(f(x_0))$.

• מיון אי רציפות.
  • רציפות - הגבול בנקודה שווה לערך בנקודה.
  • סליקה - הגבול קיים וסופי בנקודה, אך שונה מהערך בנקודה או שהפונקציה אינה מוגדרת בנקודה.
  • קפיצתית (מין ראשון) - הגבולות החד צדדיים קיימים סופיים ושונים בנקודה.
  • עיקרית (מין שני) - אחד הגבולות החד צדדיים אינו קיים או שאינו סופי.

פרק 5 - גזירות

הגדרת הנגזרת

• $f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)-f(x)}{h}$
• $limh\to 0\frac{f(x_0+h)-f(x_0)}{h}=\{h=x-x_0\}=\underset{x\to x_0}{lim}\frac{f(x)-f(x_0)}{x-x_0}$
  • הסבר לגבי שיטת ההצבה בה השתמשנו לעיל:
  • נניח כי $limh\to 0\frac{f(x_0+h)-f(x_0)}{h}=f^{\prime }(x_0)$ ונוכיח כי $\underset{x\to x_0}{lim}\frac{f(x)-f(x_0)}{x-x_0}=f^{\prime }(x_0)$, והוכחה דומה בכיוון ההפוך.
  • תהי $x_0\ne x_n\to x_0$ נגדיר את הסדרה $0\ne h_n=x_n-x_0\to 0$.
  • כיוון ש$\frac{f(x_0+h_n)-f(x_0)}{h_n}\to f^{\prime }(x_0)$ נובע כי $\frac{f(x_n)-f(x_0)}{x_n-x_0}\to f^{\prime }(x_0)$.
• אם f גזירה בנקודה, היא רציפה בנקודה:
  • צ"ל $\underset{x\to x_0}{lim}f(x)=f(x_0)$
  • לפי אריתמטיקה של גבולות זה שקול ל $\underset{x\to x_0}{lim}f(x)-f(x_0)=0$
  • לפי עקרון win (קיצור של wouldn't it be nice?) מתקיים כי $\underset{x\to x_0}{lim}f(x)-f(x_0)=\underset{x\to x_0}{lim}\frac{f(x)-f(x_0)}{x-x_0}\cdot (x-x_0)=f^{\prime }(x_0)\cdot 0=0$
• פונקציה הערך המוחלט אינה גזירה באפס
  • $(|x|{)}^{\prime }(0)=\underset{h\to 0}{lim}\frac{|h|-|0|}{h}=lim\frac{|h|}{h}$ וגבול זה אינו קיים, כיוון שהגבולות החד צדדים שונים.
  • ניתן לשים לב גם ש$|x|=\sqrt{x^2}$, וכמו כן נראה בהמשך כי$\sqrt{x}$ אינה גזירה באפס.

הנגזרות של הפונקציות האלמנטריות

• טריגו:
  • $\underset{h\to 0}{lim}\frac{1-cos(h)}{h}=\underset{h\to 0}{lim}\frac{si{n}^2(h)}{h(1+cos(h))}=\underset{h\to 0}{lim}sin(h)\cdot \frac{sin(h)}{h}\cdot \frac{1}{1+cos(h)}=0\cdot 1\cdot \frac{1}{2}=0$
  • $(sin(x){)}^{\prime }=\underset{h\to 0}{lim}\frac{sin(x+h)-sin(x)}{h}=\underset{h\to 0}{lim}\frac{sin(x)cos(h)+sin(h)cos(x)-sin(x)}{h}=\underset{h\to 0}{lim}sin(x)\cdot \frac{cos(h)-1}{h}+cos(x)\cdot \frac{sin(h)}{h}=cos(x)$
  • באופן דומה $(cos(x){)}^{\prime }=-sin(x)$
• לוג:
  • $\underset{h\to 0}{lim}\frac{log(1+h)}{h}=\underset{h\to 0}{lim}\frac{1}{h}\cdot log(1+h)=\underset{h\to 0}{lim}log\left({(1+h)}^{\frac{1}{h}}\right)=log(e)$
    • המעבר האחרון נובע מהעובדה שפונקצית הלוג רציפה.
    • (בפרט נובע כי $\underset{x\to 0}{lim}\frac{ln(1+x)}{x}=1$.)
  • $(log(x){)}^{\prime }=\underset{h\to 0}{lim}\frac{log(x+h)-log(x)}{h}=\underset{h\to 0}{lim}\frac{log\left(\frac{x+h}{x}\right)}{h}=\underset{h\to 0}{lim}\frac{1}{x}\cdot \frac{log(1+\frac{h}{x})}{\frac{h}{x}}=\frac{log(e)}{x}$
    • בפרט נובע כי $(ln(x){)}^{\prime }=\frac{1}{x}$
• אקספוננט:
  • $\underset{h\to 0}{lim}\frac{a^h-1}{h}=\{t=a^h-1,h=lo{g}_a(1+t)\}=\underset{t\to 0}{lim}\frac{t}{lo{g}_a(1+t)}=\frac{1}{lo{g}_a(e)}=\frac{1}{\frac{ln(e)}{ln(a)}}=ln(a)$
  • $(a^x{)}^{\prime }=\underset{h\to 0}{lim}\frac{a^{x+h}-a^x}{h}=\underset{h\to 0}{lim}{a}^x\cdot \frac{a^h-1}{h}=a^x\cdot ln(a)$
    • בפרט נובע כי $(e^x{)}^{\prime }=e^x$.
• חזקה:
  • $(x^{\alpha }{)}^{\prime }=\alpha x^{\alpha -1}$ לכל $\alpha \in \mathbb{R}$, הוכחה בהמשך.
    • בפרט:
    • $(1{)}^{\prime }=0$
    • $(\frac{1}{x}{)}^{\prime }=(x^{-1}{)}^{\prime }=-\frac{1}{x^2}$
    • $(\sqrt{x}{)}^{\prime }=(x^{\frac{1}{2}}{)}^{\prime }=\frac{1}{2\sqrt{x}}$

תהי f גזירה ב$x_0$ ותהי g הגזירה ב$f(x_0)$:

• $(g\circ f{)}^{\prime }(x_0)=\underset{x\to x_0}{lim}\frac{g(f(x))-g(f(x_0))}{x-x_0}$
• תהי סדרה $x_0\ne x_n\to x_0$.
• רוצים לומר ש$\frac{g(f(x_n))-g(f(x_0))}{x_n-x_0}=\frac{g(f(x_n))-g(f(x_0))}{f(x_n)-f(x_0)}\cdot \frac{f(x_n)-f(x_0)}{x_n-x_0}\to g^{\prime }(f(x_0))\cdot f^{\prime }(x_0)$.
• אמנם $f(x_n)\to f(x_0)$ בגלל שהרציפות נובעת מהגזירות, אבל לא ידוע ש$f(x_n)\ne f(x_0)$ ובמקרה זה אנחנו כופלים ומחלקים באפס.
• אם יש תת סדרה $a_n$ של $x_n$ עבורה $f(a_n)=f(x_0)$ אזי $\frac{f(a_n)-f(x_0)}{a_n-x_0}=0$ ולכן $f^{\prime }(x_0)=0$.
• לכן $g^{\prime }(f(x_0))\cdot f^{\prime }(x_0)=0$.
• כמו כן, $\frac{g(f(a_n))-g(f(x_0))}{a_n-x_0}=0$.
• לכן בכל מקרה קיבלנו כי $\frac{g(f(x_n))-g(f(x_0))}{x_n-x_0}\to g^{\prime }(f(x_0))\cdot f^{\prime }(x_0)$
• סה"כ $(g\circ f{)}^{\prime }(x_0)=g^{\prime }(f(x_0))\cdot f^{\prime }(x_0)$.

נגזרת של חזקה

• עבור $x>0$ מתקיים $(x^{\alpha }{)}^{\prime }=(e^{ln\left(x^{\alpha }\right)}{)}^{\prime }=(e^{\alpha \cdot ln(x)}{)}^{\prime }=e^{\alpha \cdot ln(x)}\cdot \frac{\alpha }{x}=x^{\alpha }\cdot \frac{\alpha }{x}=\alpha x^{\alpha -1}$
• דוגמא: חישוב הנגזרת של $x^x$

נגזרת מנה

תהיינה f,g גזירות בנקודה x כך ש $g(x)\ne 0$:

• נזכור כי $(\frac{1}{x}{)}^{\prime }=-\frac{1}{x^2}$
• אזי בנקודה x מתקיים: ${\left(\frac{f}{g}\right)}^{\prime }={(f\cdot \frac{1}{g})}^{\prime }=f^{\prime }\cdot \frac{1}{g}+f\cdot \frac{-g^{\prime }}{g^2}=\frac{f^{\prime }g-g^{\prime }f}{g^2}$

פונקציות הופכיות ונגזרתן

• פונקציות הפיכות (הוכחות והגדרות מדוייקות בבדידה).
  • פונקציה $f:[a,b]\to [c,d]$ הפיכה אם"ם היא חח"ע ועל
  • הפונקציה ההופכית היא $f^{-1}:[c,d]\to [a,b]$ ומתקיים כי $f(x)=y$ אם"ם $x=f^{-1}(y)$

• טענה: אם $f:[a,b]\to [c,d]$ רציפה בקטע $[a,b]$, אזי $f^{-1}:[c,d]\to [a,b]$ רציפה בקטע $[c,d]$.
  • הוכחה:
  • תהי $y_0\ne y_n\to y_0$, צ"ל ש $f^{-1}(y_n)\to f^{-1}(y_0)$
  • יהי גבול חלקי $x_n=f^{-1}(y_n)\to L$.
  • אזי $f(x_n)=y_n\to y_0$.
  • מצד שני, לפי רציפות הפונקציה f מתקיים $f(x_n)\to f(L)$.
  • לכן $f(L)=y_0$ ולכן $L=f^{-1}(y_0)$.

• טענה: תהי $f:[a,b]\to [c,d]$ הפיכה ורציפה. ונניח כי היא גזירה בנק' $a<x_0<b$ כך ש $f^{\prime }(x_0)\ne 0$.

אזי $f^{-1}$ גזירה בנק' $f(x_0)$ ומתקיים כי

$(f^{-1}{)}^{\prime }(f(x_0))=\frac{1}{f^{\prime }(x_0)}$ או בנוסח אחר-

$(f^{-1}{)}^{\prime }(x)=\frac{1}{f^{\prime }(f^{-1}(x))}$

• • הוכחה:
  • $(f^{-1}{)}^{\prime }(f(x_0))=\underset{y\to f(x_0)}{lim}\frac{f^{-1}(y)-f^{-1}(f(x_0))}{y-f(x_0)}$
  • תהי $f(x_0)\ne y_n\to f(x_0)$ ונסמן $x_n=f^{-1}(y_n)$.
  • אזי מתוך רציפות וחח"ע נובע כי $x_0\ne x_n\to f^{-1}(f(x_0))=x_0$
  • $\frac{f^{-1}(y_n)-f^{-1}(f(x_0))}{y_n-f(x_0)}=\frac{x_n-x_0}{f(x_n)-f(x_0)}\to \frac{1}{f^{\prime }(x_0)}$

• דוגמא חשובה:
• $tan:(-\frac{\pi }{2},\frac{\pi }{2})\to \mathbb{R}$ הפיכה וההופכית שלה נקראית $arctan$.
• $ta{n}^2(x)+1=\frac{si{n}^2(x)}{co{s}^2(x)}+1=\frac{1}{co{s}^2(x)}$
• $arcta{n}^{\prime }(x)=\frac{1}{\frac{1}{co{s}^2(arctan(x))}}=\frac{1}{ta{n}^2(arctan(x))+1}=\frac{1}{1+x^2}$

פרק 6 - חקירה

משפטי חקירת פונקציות

• משפט ערך הביניים.
• תהי f רציפה ב$[0,1]$ כך ש$f(1)=2$, הוכיחו שקיימת נק' $c\in [0,1]$ עבורה $f(c)=\frac{1}{c}$
  • נעביר אגף ונביט בפונקציה $h(x)=f(x)-\frac{1}{x}$ שצריך למצוא שורש שלה.
  • $h(1)>0$.
  • $\underset{x\to 0^{+}}{lim}h(x)=f(0)-\mathrm{\infty }=-\mathrm{\infty }$ ולכן קיימת נקודה $0<d<1$ עבורה $h(d)<0$.
  • לפי משפט ערך הביניים בקטע $[d,1]$ קיימת נק' המאפסת את הפונקציה h.

• משפטי ויירשטראס.
  • פונקציה רציפה בקטע סופי סגור - חסומה.
  • פונקציה רציפה בקטע סופי סגור - מקבלת מינימום ומקסימום.

• משפט פרמה.
  • אם פונקציה גזירה בנק' קיצון מקומי, הנגזרת שווה שם לאפס.
  • ההפך אינו נכון.
• משפט רול.
  • פונקציה רציפה בקטע סגור, וגזירה בקטע הפתוח, שמקבלת את אותו ערך בקצוות - הנגזרת שלה מתאפסת בקטע הפתוח.
  • לפולינום יש לכל היותר n שורשים שונים.
• משפט לגראנז'.
  • פונקציה רציפה בקטע סגור, וגזירה בקטע הפתוח מקבלת את השיפוע בין שתי נקודות הקצה בנגזרת בנק' כלשהי.
• משפט לגראנז' המוכלל.
  • שתי פונקציות רציפות בקטע סגור, גזירות בקטע הפתוח, והנגזרת של האחת אינה מתאפסת. אזי מנת הנגזרות שווה למנת השיפועים בנק' מסויימת.

• הוכחת משפט לגראנז' המוכלל, שמוכיח גם את משפט לגראנז' עצמו כמקרה פרטי.
  • ראשית, כיוון ש$g^{\prime }(x)\ne 0$ בקטע $(a,b)$ נובע לפי רול כי $g(a)\ne g(b)$ ולכן מותר לחלק בהפרש ביניהם.
  • $h(x)=f(x)-f(a)-\frac{f(b)-f(a)}{g(b)-g(a)}(g(x)-g(a))$
  • $h(a)=h(b)=0$ ולכן לפי רול קיימת נק' $c\in (a,b)$ עבורה $h^{\prime }(c)=0$ וזה מה שרצינו להוכיח.
  • (שימו לב שמותר לחלק ב$g^{\prime }(c)$.)
  • עבור $g(x)=x$ נקבל את משפט לאגראנז' הרגיל.

קשר בין הנגזרת לפונקציה

• פונקציה גזירה עולה אם"ם הנגזרת שלה גדולה או שווה אפס.
• פונקציה עולה ממש אם"ם הנגזרת שלה גדולה או שווה אפס, ולא מתאפסת על קטע.

כלל לופיטל

• כלל לופיטל (הוכחה לאפס חלקי אפס בנקודה סופית).
• כיצד להעזר בלופיטל בכל אחד מהמקרים הבעייתיים.