אנליזת פורייה - ארז שיינר

תקציר ההרצאות

• ההרצאות מבוססות בחלקן על הספר המצויין 'טורי פוריה' של זעפרני ופינקוס.

הרצאה 1 - הקדמה ומקדמי פוריה

הקדמה - גלים

• מבלי להגדיר גל במפורש, גל הוא תופעה מחזורית.
• לגל שהוא פונקציה במשתנה אחד של ציר הזמן יש שלוש תכונות:
  • תדר או אורך גל (אחד חלקי המחזור או המחזור)
  • אמפליטודה (מרחק בין המקסימום למינימום)
  • פאזה (מהי נק' ההתחלה של המחזור).
• אנחנו נתרכז כמעט באופן בלעדי בפונקציות הטריגונומטריות סינוס וקוסינוס, ונקרא להם גלים טריגונומטריים.

• מדוע דווקא סינוס וקוסינוס?
• למדנו במד"ר על המשוואה [math]\displaystyle{ y''=-k^2y }[/math] המתארת תנועה על מסה המחוברת לקפיץ
• זו למעשה תנועה כללית של גל - ככל שהוא מתרחק, גדל הכוח שמושך אותו למרכז. מיתר גיטרה הוא דוגמא טובה נוספת.
• הפתרון הכללי למד"ר הוא [math]\displaystyle{ y=a\sin(kt)+b\cos(kt) }[/math].
• הקבוע [math]\displaystyle{ k }[/math] קובע את התדר של כל גל.
• הקבועים [math]\displaystyle{ a,b }[/math] קובעים את האמפליטודה של כל גל.
• מה לגבי הפאזה?
  • בפונקציה [math]\displaystyle{ a\sin(kt+t_0) }[/math], הקבוע [math]\displaystyle{ t_0 }[/math] קובע את הפאזה.
  • ניתן להציג כל גל כזה באמצעות סינוס וקוסינוס ללא פאזה:
    • [math]\displaystyle{ a\sin(kt+t_0)=(a\sin(t_0))cos(kt)+(a\cos(t_0))sin(kt) }[/math]

• האם גם ההפך נכון? כלומר האם כל צירוף לינארי [math]\displaystyle{ a\sin(kt)+b\cos(kt) }[/math] ניתן להציג כגל יחיד?
• תשובה: כן.
• הוכחה:
  • נסמן [math]\displaystyle{ z=a+bi=rcis(\theta) }[/math]
  • כלומר [math]\displaystyle{ a\sin(kt)+b\cos(kt)=r\sin(\theta)sin(kt)+r\cos(\theta)cos(kt)=rcos(kt-\theta) }[/math]
• שימו לב:
  • סכמנו שני גלים מאותו תדר עם פאזה אפס, וקיבלנו גל חדש.
  • הגל החדש הוא מאותו תדר כמו שני הגלים.
  • לגל החדש יש פאזה שאינה אפס.
  • האפליטודה של הגל החדש היא [math]\displaystyle{ r=\sqrt{a^2+b^2} }[/math].

• האם כל פונקציה היא סכום של גלים?
• בהנתן פונקציה שהיא סכום של גלים, כיצד נמצא מיהם הגלים המרכיבים אותה?
• האם יש דרך יחידה להרכיב פונקציה מגלים? (למעשה כבר ראינו שלא באופן כללי - הרי הצלחנו להציג גל אחד כסכום של שני גלים אחרים).
• למה בכלל מעניין אותנו לפרק פונקציה לגלים?
• במהלך ההרצאות נענה (לפחות חלקית) על השאלות הללו.

טורי פורייה ומקדמי פוריה

• טור פורייה הוא טור מהצורה [math]\displaystyle{ f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty \left[a_n\cos(nx)+b_n\sin(nx)\right] }[/math]

• אם פונקציה שווה לטור פורייה שלה, מהם המקדמים [math]\displaystyle{ a_n,b_n }[/math]?

חישובים להקדמה

• ראשית נזכור את הנוסחאות הטריגונומטריות:
  • [math]\displaystyle{ \sin(a)\sin(b)=\frac{1}{2}\left[\cos(a-b)-\cos(a+b)\right] }[/math]
  • [math]\displaystyle{ \cos(a)\cos(b)=\frac{1}{2}\left[\cos(a+b)+\cos(a-b)\right] }[/math]
• כעת, לכל [math]\displaystyle{ 0\neq n\in\mathbb{N} }[/math] נקבל:
  • [math]\displaystyle{ \frac{1}{\pi}\int_{-\pi}^{\pi}\sin(nx)\sin(nx)dx = \frac{1}{2\pi}\int_{-\pi}^{\pi}(1-\cos(2nx))dx = \frac{1}{2\pi}\left[x-\frac{1}{2n}\sin(2nx)\right]_{-\pi}^{\pi}=1 }[/math]
• עבור [math]\displaystyle{ n\neq k \in \mathbb{N} }[/math] נקבל:
  • [math]\displaystyle{ \int_{-\pi}^{\pi}\sin(nx)\sin(kx)dx = \frac{1}{2}\int_{-\pi}^{\pi}(\cos((n-k)x)-\cos((n+k)x))dx = \frac{1}{2}\left[\frac{\sin((n-k)x)}{n-k}-\frac{\sin((n+k)x)}{n+k}\right]_{-\pi}^{\pi}=0 }[/math]
  • שימו לב כי השתמשנו כאן בעובדה ש[math]\displaystyle{ n-k,n+k\neq 0 }[/math].
• באופן דומה, לכל [math]\displaystyle{ 0\neq n\in\mathbb{N} }[/math] נקבל:
  • [math]\displaystyle{ \frac{1}{\pi}\int_{-\pi}^{\pi}\cos(nx)\cos(nx)dx = \frac{1}{2\pi}\int_{-\pi}^{\pi}(\cos(2nx)+1)dx = \frac{1}{2\pi}\left[\frac{1}{2n}\sin(2nx)+x\right]_{-\pi}^{\pi}=1 }[/math]
• עבור [math]\displaystyle{ n\neq k \in \mathbb{N} }[/math] נקבל:
  • [math]\displaystyle{ \int_{-\pi}^{\pi}\cos(nx)\cos(kx)dx = \frac{1}{2}\int_{-\pi}^{\pi}(\cos((n+k)x)+\cos((n-k)x))dx = \frac{1}{2}\left[\frac{\sin((n-k)x)}{n+k}+\frac{\sin((n-k)x)}{n+k}\right]_{-\pi}^{\pi}=0 }[/math]
  • שימו לב כי השתמשנו כאן בעובדה ש[math]\displaystyle{ n-k,n+k\neq 0 }[/math].
• עבור [math]\displaystyle{ n,k\in \mathbb{N} }[/math] נקבל:
  • [math]\displaystyle{ \int_{-\pi}^{\pi}\cos(nx)\sin(kx)dx=0 }[/math] כיוון שמדובר באינטגרל בקטע סימטרי על פונקציה אי זוגית.
• ולבסוף, עבור [math]\displaystyle{ n=0 }[/math] נקבל
  • [math]\displaystyle{ \frac{1}{\pi}\int_{-\pi}^{\pi}\cos(0)\cos(0)dx=\frac{1}{\pi}\int_{-\pi}^{\pi}1dx=2 }[/math]
• שימו לב שכאשר מציבים 0 בsin מקבלים אפס, ולכן אין צורך בבדיקה הזו.

• הערה חשובה:
  • למעשה כלל החישובים שעשינו לעיל מוכיחים שהקבוצה [math]\displaystyle{ \{\frac{1}{\sqrt{2}},sin(x),cos(x),sin(2x),cos(2x),...\} }[/math] מהווה קבוצה אורתונורמלית לפי המכפלה הפנימית [math]\displaystyle{ \langle f,g\rangle=\frac{1}{\pi}\int_{-\pi}^{\pi}(f\cdot g) dx }[/math]

מקדמי הטור

• כעת תהי פונקציה ששווה לטור פורייה, ועוד נניח שהטור מתכנס במ"ש.
• [math]\displaystyle{ \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(kx)dx = \frac{1}{\pi}\int_{-\pi}^{\pi}\left(\frac{a_0}{2}+\sum_{n=1}^\infty \left[a_n\cos(nx)+b_n\sin(nx)\right]\right)\cos(kx)dx= }[/math]
• [math]\displaystyle{ =\frac{1}{\pi}\int_{-\pi}^{\pi}\left(\frac{a_0}{2}\cos(kx)+\sum_{n=1}^\infty \left[a_n\cos(nx)\cos(kx)+b_n\sin(nx)\cos(kx)\right]\right)dx= }[/math]
• כיוון שהטור מתכנס במ"ש, מותר לנו לעשות אינטגרציה איבר איבר
• [math]\displaystyle{ =\frac{1}{\pi}\int_{-\pi}^{\pi}\frac{a_0}{2}\cos(kx)dx + \sum_{n=1}^\infty \left[\frac{1}{\pi}\int_{-\pi}^{\pi}\left(a_n\cos(nx)\cos(kx)+b_n\sin(nx)\cos(kx)\right)dx\right] }[/math]
• לפי חישובי האינטגרלים לעיל, כמעט הכל מתאפס וסה"כ נקבל:
• [math]\displaystyle{ a_k=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(kx)dx }[/math]
• שימו לב שחישוב זה נכון בפרט עבור [math]\displaystyle{ k=0 }[/math].
• באופן דומה נקבל כי [math]\displaystyle{ b_k=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin(kx)dx }[/math]

• הוכחנו שאם פונקציה שווה לטור פורייה, והטור מתכנס במ"ש, אזי הוא יחיד והמקדמים שלו נקבעים על ידי הנוסחאות לעיל.
• השאלה היא אילו פונקציות שוות לטור פורייה.
• באופן מיידי, ברור שטור פורייה הוא פונקציה עם מחזור [math]\displaystyle{ 2\pi }[/math].
• לכן בדר"כ אנו שואלים האם ההמשך המחזורי של הפונקציה שווה לטור פורייה:
  • תהי פונקציה [math]\displaystyle{ f }[/math], נגדיר את ההמשך המחזורי שלה [math]\displaystyle{ g }[/math] על ידי:
  • לכל [math]\displaystyle{ k\in\mathbb{Z} }[/math] ולכל [math]\displaystyle{ x\in [-\pi+2\pi k,\pi+2\pi k) }[/math] נגדיר [math]\displaystyle{ g(x)=f(x-2\pi k) }[/math].
  • ברור ש [math]\displaystyle{ g(x+2\pi) = g(x) }[/math], כלומר קיבלנו פונקציה מחזורית.
  • ניתן גם לרשום בנוסחא מקוצרת [math]\displaystyle{ g(x)=f(x-2\pi\lfloor\frac{x+\pi}{2\pi}\rfloor) }[/math]

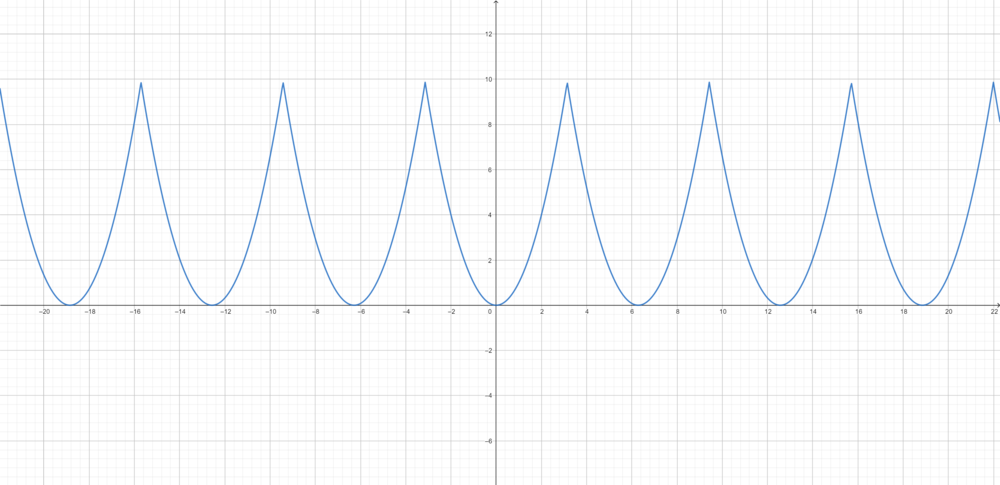
• לדוגמא, ההמשך המחזורי של [math]\displaystyle{ x^2 }[/math]:

דוגמא

• נחשב את מקדמי הפורייה של ההמשך המחזורי של [math]\displaystyle{ x^2 }[/math]
• שימו לב, מקדמי הפורייה של פונקציה וההמשך המחזורי שלה זהים, כיוון שערך הפונקציה בנקודה אחת לא משפיע על האינטגרל.

[math]\displaystyle{ b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}x^2\sin(nx)dx=0 }[/math].

• שימו לב: מקדמי הפורייה של הסינוסים תמיד יתאפסו עבור פונקציה זוגית, ומקדמי הפורייה של הקוסינוסים תמיד יתאפסו עבור פונקציה אי זוגית.

[math]\displaystyle{ a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}x^2dx =\frac{2}{\pi}\int_{0}^{\pi}x^2dx= \frac{2}{\pi}\left[\frac{1}{3}x^3\right]_{0}^{\pi} = \frac{2\pi^2}{3} }[/math]

[math]\displaystyle{ a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}x^2\cos(nx)dx=\frac{2}{\pi}\int_{0}^{\pi}x^2\cos(nx)dx =\left\{\begin{array}{lr}f'=\cos(nx) & g=x^2\\ f= \frac{\sin(nx)}{n} & g'=2x\end{array}\right\}= }[/math]

[math]\displaystyle{ =\frac{2}{\pi}\left[\frac{x^2\sin(nx)}{n}\right]_0^{\pi} - \frac{4}{n\pi}\int_{0}^{\pi}x\sin(nx)dx = - \frac{4}{n\pi}\int_{0}^{\pi}x\sin(nx)dx= \left\{\begin{array}{lr}f'=\sin(nx) & g=x\\ f= -\frac{\cos(nx)}{n} & g'=1\end{array}\right\}= }[/math]

[math]\displaystyle{ - \frac{4}{n\pi}\left[\frac{-x\cos(nx)}{n}\right]_0^\pi + \frac{4}{n^2\pi}\int_0^\pi \cos(nx)dx=\frac{4\pi\cos(\pi n)}{n^2\pi}+\frac{4}{n^3\pi}\left[sin(nx)\right]_0^\pi = \frac{4(-1)^n}{n^2} }[/math]

• שימו לב כי לכל [math]\displaystyle{ n\in\mathbb{N} }[/math] מתקיים כי [math]\displaystyle{ cos(n\pi)=(-1)^n }[/math]

• סה"כ אם ההמשך המחזורי של [math]\displaystyle{ x^2 }[/math] שווה לטור פורייה שמתכנס במ"ש, אזי טור זה הוא:

[math]\displaystyle{ \frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4(-1)^n}{n^2}cos(nx) }[/math]

• נניח (ונוכיח בהמשך) שטור זה אכן שווה לפונקציה ונציב [math]\displaystyle{ \pi }[/math].
• [math]\displaystyle{ \pi^2 = \frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4}{n^2} }[/math]
• ונקבל את הסכום המפורסם

[math]\displaystyle{ \sum_{n=1}^\infty \frac{1}{n^2}=\frac{\pi^2}{6} }[/math]

הרצאה 2 - למת רימן לבג, גרעין דיריכלה

מרחבי מכפלה פנימית שאינם ממימד סופי והיטלים

• פונקציה נקראת רציפה למקוטעין בקטע סופי אם היא רציפה פרט אולי למספר סופי של נקודות בהן יש אי רציפות סליקות או ממין ראשון (קפיצתי). כמו בן, הגבולות החד צדדיים בקצות הקטע הם סופיים.
• פונקציה נקראת רציפה למקוטעין בקטע כללי, אם היא רציפה למקוטעין בכל תת קטע סופי.
• E הוא המרחב הוקטורי של כל הפונקציות הרציפות למקוטעין [math]\displaystyle{ f:[-\pi,\pi]\to\mathbb{C} }[/math] מעל השדה [math]\displaystyle{ \mathbb{C} }[/math].
• [math]\displaystyle{ \langle f,g\rangle=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\overline{g(x)}dx }[/math] היא מכפלה פנימית מעל E.
• נביט בנורמה המושרית [math]\displaystyle{ ||f||^2=\langle f,f\rangle }[/math]

• כעת נוכיח מספר תכונות של היטלים במרחבי מכפלה פנימית.
• יש לנקוט בזהירות מיוחדת בנושא זה, כיוון שאנו עוסקים במרחבים שאינם נוצרים סופית (אין להם בסיס סופי או מימד).
• ייתכן שהוכחתם חלק מהמשפטים הבאים רק עבור מרחבים נוצרים סופית.

• תהי קבוצה אורתונורמלית סופית [math]\displaystyle{ \{e_1,...,e_n\} }[/math], ונקרא למרחב שהיא פורשת W.
• לכל וקטור [math]\displaystyle{ v\in V }[/math] נגדיר את ההיטל של [math]\displaystyle{ v }[/math] על W על ידי [math]\displaystyle{ \widetilde{v}=\sum_{i=1}^n\langle v,e_i\rangle e_i }[/math]
• נוכיח מספר תכונות לגבי ההיטל הזה:

• מתקיים כי [math]\displaystyle{ \langle v,\widetilde{v}\rangle = \langle \widetilde{v},\widetilde{v}\rangle=\sum_{i=1}^n |\langle v,e_i\rangle|^2 }[/math]
  • הוכחה:
  • [math]\displaystyle{ \langle v,\widetilde{v}\rangle = \langle v,\sum_{i=1}^n\langle v,e_i\rangle e_i\rangle = \sum_{i=1}^n \overline{\langle v,e_i\rangle}\langle v,e_i\rangle = \sum_{i=1}^n |\langle v,e_i\rangle|^2 }[/math]
  • [math]\displaystyle{ \langle \widetilde{v},\widetilde{v}\rangle = \langle \sum_{i=1}^n\langle v,e_i\rangle e_i,\sum_{i=1}^n\langle v,e_i\rangle e_i\rangle = \sum_{i=1}^n |\langle v,e_i\rangle|^2 }[/math]
  • המעבר האחרון נכון כיוון ש [math]\displaystyle{ \{e_1,...,e_n\} }[/math] אורתונורמלית.

• מתקיים כי [math]\displaystyle{ ||v||^2=||v-\widetilde{v}||^2+||\widetilde{v}||^2 }[/math]
  • הוכחה:
  • [math]\displaystyle{ \langle v-\widetilde{v},v-\widetilde{v}\rangle = \langle v,v\rangle - \langle v,\widetilde{v}\rangle - \langle \widetilde{v},v\rangle + \langle \widetilde{v},\widetilde{v}\rangle }[/math]
  • נזכור כי [math]\displaystyle{ \langle v,\widetilde{v}\rangle = \langle \widetilde{v},\widetilde{v}\rangle }[/math].
  • לכן קיבלנו כי [math]\displaystyle{ ||v-\widetilde{v}||^2 = ||v||^2 - ||\widetilde{v}||^2 }[/math]

• מסקנה מיידית: [math]\displaystyle{ ||\widetilde{v}||\leq ||v|| }[/math]

אי שיוויון בסל

• כעת תהי קבוצה אורתונורמלית אינסופית [math]\displaystyle{ \{e_1,e_2,...\} }[/math].
• לכל [math]\displaystyle{ v\in V }[/math] מתקיים כי [math]\displaystyle{ \sum_{i=1}^\infty |\langle v,e_i\rangle|^2 \leq ||v||^2 }[/math]
  • הוכחה:
  • ראינו שלכל n מתקיים כי [math]\displaystyle{ \sum_{i=1}^n |\langle v,e_i\rangle|^2 \leq ||v||^2 }[/math].
  • כלומר סדרת הסכומים החלקיים של הטור החיובי חסומה על ידי [math]\displaystyle{ ||v||^2 }[/math] ולכן הטור מתכנס למספר שקטן או שווה לו.

• בפרט נובע כי

[math]\displaystyle{ \lim_{n\to\infty}|\langle v,e_i\rangle|=0 }[/math]

למת רימן לבג

• ראינו כי [math]\displaystyle{ \{\sin(x),\cos(x),\sin(2x),\cos(2x),...\} }[/math] היא קבוצה אורתונורמלית ב[math]\displaystyle{ E }[/math] (כרגע אנו לא צריכים את הפונקציה הקבועה).
• כמו כן לכל פונקציה f הגדרנו מקדמי פורייה ע"י:
• לכל [math]\displaystyle{ 1\leq n\in \mathbb{N} }[/math] הגדרנו [math]\displaystyle{ a_n=\langle f,\cos(nx)\rangle }[/math], ו[math]\displaystyle{ b_n=\langle f,\sin(nx)\rangle }[/math]

• נובע מאי שיוויון בסל כי המקדמים שואפים לאפס.
• כלומר:

[math]\displaystyle{ \lim_{n\to\infty}\frac{1}{\pi}\int_{-\pi}^\pi f(x)\cos(nx)dx = 0 }[/math]

[math]\displaystyle{ \lim_{n\to\infty}\frac{1}{\pi}\int_{-\pi}^\pi f(x)\sin(nx)dx = 0 }[/math]

• למת רימן-לבג: תהי [math]\displaystyle{ g }[/math] רציפה למקוטעין בקטע [math]\displaystyle{ [0,\pi] }[/math], אזי:

[math]\displaystyle{ \lim_{n\to\infty}\int_{0}^\pi g(t)\sin\left(\left(n+\frac{1}{2}\right)t\right)dt = 0 }[/math]

• הוכחה:
  • [math]\displaystyle{ \int_{0}^\pi g(t)\sin\left(\left(n+\frac{1}{2}\right)t\right)dt = \int_{0}^\pi g(t)\cos(\frac{t}{2})\sin(nt) dt+\int_{0}^\pi g(t)\sin(\frac{t}{2})\cos(nt) dt }[/math]
  • נגדיר את שתי הפונקציות [math]\displaystyle{ h_s(t)=\begin{cases}g(t)\sin(\frac{t}{2}) & 0\leq t\leq \pi \\ 0 & -\pi\leq t \lt 0\end{cases} }[/math] ו [math]\displaystyle{ h_c(t)=\begin{cases}g(t)\cos(\frac{t}{2}) & 0\leq t\leq \pi \\ 0 & -\pi\leq t \lt 0\end{cases} }[/math]
  • קל לראות כי שתי הפונקציות רציפות למקוטעין, כלומר [math]\displaystyle{ h_c,h_s\in E }[/math].
  • ביחד נקבל כי [math]\displaystyle{ \int_{0}^\pi g(t)\sin\left(\left(n+\frac{1}{2}\right)t\right)dt = \int_{-\pi}^\pi h_c(t)sin(nt)dt + \int_{-\pi}^\pi h_s(t)sin(nt)dt \to 0 }[/math]

גרעין דיריכלה

• גרעין דיריכלה הוא הפונקציה [math]\displaystyle{ D_n(x)= \frac{\sin\left(\left(n+\frac{1}{2}\right)t\right)}{2\sin(\frac{t}{2})} }[/math]

• טענה: [math]\displaystyle{ D_n(x)=\frac{1}{2}+\sum_{k=1}^n \cos(kt) }[/math] בכל נקודה [math]\displaystyle{ t\neq 2\pi k }[/math]
  • הוכחה:
  • נכפל ב[math]\displaystyle{ 2\sin(\frac{t}{2}) }[/math] ונקבל בצד שמאל:
  • [math]\displaystyle{ \sin(\frac{t}{2}) + 2\sin(\frac{t}{2})\cos(t) + 2\sin(\frac{t}{2})\cos(2t)+...+2\sin(\frac{t}{2})\cos(nt) }[/math]
  • נבחין בזהות הטריגונומטרית [math]\displaystyle{ 2\sin(a)\cos(b) = \sin(b+a)-\sin(b-a) }[/math]
  • ובפרט [math]\displaystyle{ 2\sin(\frac{t}{2})\cos(kt) = \sin(kt+\frac{t}{2}) - \sin(kt-\frac{t}{2}) }[/math]
  • ביחד נקבל [math]\displaystyle{ \sin(\frac{t}{2}) + \sin(t+\frac{t}{2})-\sin(t-\frac{t}{2}) + \sin(2t+\frac{t}{2}) - \sin(2t-\frac{t}{2})+...+\sin(nt+\frac{t}{2}) - \sin(nt-\frac{t}{2}) = \sin(nt+\frac{t}{2}) = \sin\left(\left(n+\frac{1}{2}\right)t\right) }[/math]

• נשים לב כי הפונקציה [math]\displaystyle{ 2\sin(\frac{t}{2}) }[/math] מתאפסת בנקודות [math]\displaystyle{ t=2\pi k }[/math], בנקודות אלו לגרעין דיריכלה יש אי רציפות סליקה.
• זה נכון כיוון שפרט לנקודות אלו מדובר בפונקציה רציפה.
• כמו כן, גרעין דיריכלה מחזורי [math]\displaystyle{ 2\pi }[/math] כיוון שהוא סכום של פונקציות מחזוריות [math]\displaystyle{ 2\pi }[/math].

הסכומים החלקיים של טור פוריה

• תהיה נקודה x, נביט בסדרת הסכומים החלקיים של טור הפוריה המתאים לפונקציה [math]\displaystyle{ f }[/math] שהיא מחזורית [math]\displaystyle{ 2\pi }[/math]:

[math]\displaystyle{ S_n = \frac{a_0}{2} + \sum_{k=1}^n a_k\cos(kx)+b_k\sin(kx) }[/math]

• נציב את מקדמי פוריה ונקבל כי:

[math]\displaystyle{ S_n = \frac{1}{\pi}\int_{-\pi}^\pi \frac{1}{2}f(t)dt + \sum_{k=1}^n \left[\frac{1}{\pi}\int_{-\pi}^\pi f(t)\cos(kt)dt\right]\cos(kx)+\left[\frac{1}{\pi}\int_{-\pi}^\pi f(t)\sin(kt)dt\right]\sin(kx)= }[/math]

[math]\displaystyle{ = \frac{1}{\pi}\int_{-\pi}^\pi\left[\frac{1}{2}f(t)+\sum_{k=1}^n f(t)\left(\cos(kt)\cos(kx) + \sin(kt)\sin(kx)\right)\right]dt= }[/math]

[math]\displaystyle{ =\frac{1}{\pi}\int_{-\pi}^\pi f(t)\left[\frac{1}{2}+\sum_{k=1}^n \cos(k(t-x))\right]dt }[/math]

• זה בעצם גרעין דיריכלה, כלומר קיבלנו כי:

[math]\displaystyle{ S_n = \frac{1}{\pi}\int_{-\pi}^\pi f(t)D_n(t-x)dt }[/math]

• שימו לב ששינוי מספר סופי של נקודות לא משפיע על האינטגרל, ולכן נקודות אי הרציפות הסליקות של גרעין דיריכלה לא פוגעות בהוכחה.

• טענה: תהי [math]\displaystyle{ f }[/math] פונקציה מחזורית [math]\displaystyle{ 2\pi }[/math]. אזי לכל [math]\displaystyle{ a\in\mathbb{R} }[/math] מתקיים כי:

[math]\displaystyle{ \int_{-\pi}^\pi f(x)dx = \int_{-\pi+a}^{\pi+a} f(x)dx }[/math]

• כלומר, השטח מתחת לגרף הפונקציה שווה על כל קטע באורך [math]\displaystyle{ 2\pi }[/math].
  • הוכחה:

[math]\displaystyle{ \int_{-\pi+a}^{\pi+a} f(x)dx = \int_{-\pi+a}^{\pi} f(x)dx + \int_{\pi}^{\pi+a} f(x)dx }[/math]

נבצע הצבה [math]\displaystyle{ t=x-2\pi }[/math] באינטגרל השני ונקבל:

[math]\displaystyle{ \int_{\pi}^{\pi+a} f(x)dx = \{t=x-2\pi, dt=dx\} = \int_{-\pi}^{-\pi+a}f(t+2\pi)dt = \int_{-\pi}^{-\pi+a}f(t)dt = \int_{-\pi}^{-\pi+a}f(x)dx }[/math]

ביחד נקבל כי:

[math]\displaystyle{ \int_{-\pi+a}^{\pi+a} f(x)dx=\int_{-\pi+a}^{\pi} f(x)dx + \int_{-\pi}^{-\pi+a}f(x)dx = \int_{-\pi}^\pi f(x)dx }[/math]

• נחזור לסכומים החלקיים ונבצע הצבה:

[math]\displaystyle{ S_n = \frac{1}{\pi}\int_{-\pi}^\pi f(t)D_n(x-t)dt = \{ u=t-x, du=dt\} = \frac{1}{\pi}\int_{-\pi-x}^{\pi-x} f(x+u)D_n(u)du }[/math]

כיוון שגרעין דיריכלה ו[math]\displaystyle{ f }[/math] הן מחזוריות, נקבל:

[math]\displaystyle{ S_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x+u)D_n(u)du=\frac{1}{\pi}\int_{-\pi}^{\pi} f(x+t)D_n(t)dt }[/math]

הרצאה 3 התכנסות נקודתית של טורי פוריה

סימונים והגדרות

• נסמן את הגבול החד צדדי מימין ב[math]\displaystyle{ f(d^+)=\lim_{x\to d^+}f(x) }[/math].
• נסמן את הגבול החד צדדי משמאל ב[math]\displaystyle{ f(d^-)=\lim_{x\to d^-}f(x) }[/math].
• שימו לב: אם הפונקציה רציפה למקוטעין, הערכים הללו תמיד מוגדרים.

• נגדיר את הנגזרת הימנית ע"י [math]\displaystyle{ f'(d^+) = \lim_{x\to d^+}\frac{f(x)-f(d^+)}{x-d} }[/math].
• נגדיר את הנגזרת השמאלית ע"י [math]\displaystyle{ f'(d^-) = \lim_{x\to d^-}\frac{f(x)-f(d^-)}{x-d} }[/math].
• שימו לב: ייתכן ש[math]\displaystyle{ f'(d^+)=f'(d^-) }[/math] אך הפונקציה אינה גזירה בd. זה יקרה אם היא לא רציפה בנקודה.

דוגמא:

• נביט בפונקציה [math]\displaystyle{ f(x)=\frac{x}{|x|} }[/math]
• מתקיים כי [math]\displaystyle{ f(0^+)=1 }[/math], ו[math]\displaystyle{ f(0^-)=-1 }[/math].
• כמו כן מתקיים כי [math]\displaystyle{ f'(0^+)=f'(0^-)=0 }[/math].

כמובן שהפונקציה אינה רציפה ואינה גזירה ב0.

משפט דיריכלה - התכנסות נקודתית של טור פוריה

• תהי [math]\displaystyle{ f }[/math] פונקציה מחזורית [math]\displaystyle{ 2\pi }[/math], רציפה למקוטעין כך שבכל נקודה הנגזרות החד צדדיות שלה קיימות וסופיות.
• אזי לכל [math]\displaystyle{ x\in\mathbb{R} }[/math] הטור עם מקדמי הפוריה של [math]\displaystyle{ f }[/math] מתכנס:

[math]\displaystyle{ \frac{f(x^+)+f(x^-)}{2}=\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx) + b_n\sin(nx) }[/math]

• בפרט, בכל נקודה בה הפונקציה רציפה טור הפוריה מתכנס נקודתית לפונקציה, ובכל נקודה בה יש אי רציפות קפיצתית טור הפוריה מתכנס לממוצע הגבולות מימין ומשמאל.

הוכחה

• תהי נקודה [math]\displaystyle{ x\in\mathbb{R} }[/math].
• נביט בפונקציה [math]\displaystyle{ g(t) = \frac{f(x+t) - f(x^+)}{2\sin(\frac{t}{2})} }[/math]
• [math]\displaystyle{ \lim_{t\to 0^+}g(t) = \lim_{t\to 0^+}\frac{f(x+t) - f(x^+)}{t}\frac{t}{2\sin(\frac{t}{2})} = f'(x^+) }[/math]
• כיוון שהנגזרות החד צדדיות קיימות וסופיות, קיבלנו ש[math]\displaystyle{ g(t) }[/math] רציפה למקוטעין בקטע [math]\displaystyle{ [0,\pi] }[/math].