הבדלים בין גרסאות בדף "המשפט היסודי של החשבון האינטגרלי"
מתוך Math-Wiki
לב זלוטניק (שיחה | תרומות) (←סעיף א') |
לב זלוטניק (שיחה | תרומות) (←הוכחה) |
||
| שורה 30: | שורה 30: | ||
<math>\blacksquare </math> | <math>\blacksquare </math> | ||
| + | |||
| + | === סעיף ב'=== | ||
| + | שלום | ||
גרסה מ־20:55, 27 במרץ 2012
תוכן עניינים
המשפט
תהי  מוגדרת, חסומה ואינטגרבילית ב-
מוגדרת, חסומה ואינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . נגדיר גם:
. נגדיר גם: ![\forall x \in [a,b]: A(x):= \int_{a}^{x} f(t)dt](/images/math/d/5/c/d5cdf40dff23af50b5e4a2ddc27970b2.png) . אזי מתקיים:
. אזי מתקיים:
א) 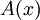 רציפה.
רציפה.
ב)לכל ![x_{0} \in [a,b]](/images/math/5/1/9/519abfe29313f54587c4ffad9895b087.png) שבו
שבו 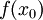 רציפה,
רציפה, 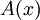 גזירה ו-
גזירה ו- 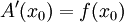 .
.
ג) אם  רציפה בכל
רציפה בכל ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , ו-F פונקציה קדומה של f, מתקיימת נוסחת ניוטון-לייבניץ:
, ו-F פונקציה קדומה של f, מתקיימת נוסחת ניוטון-לייבניץ: 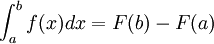 .
.
הוכחה
סעיף א'
נקח ![x \in [a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) כלשהו ו-
כלשהו ו-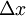 "קטן" כך ש-
"קטן" כך ש-![x+\Delta x \in [a,b]](/images/math/5/9/7/5975d5cd7e8bd0f64dfe5aa6a1877385.png) . לפי הגדרה:
. לפי הגדרה: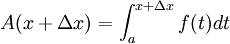 ולכן
ולכן
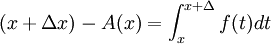 .
נתון ש-f חסומה, נגיד
.
נתון ש-f חסומה, נגיד 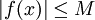 .
.
לכן מתקיים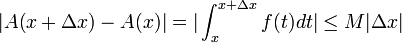 .
.
כעת נשאיף את 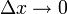 , אגף ימין שואף ל-0 .
לכן:
, אגף ימין שואף ל-0 .
לכן:
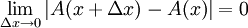 ומכך נובע ש:
ומכך נובע ש:
![\lim_{\Delta x \to 0}[A(x+\Delta x)-A(x)]=0](/images/math/1/3/7/1375310a0443665e243a8fd5c3c0c3c8.png) ולכן מתקיים תנאי הרציפות,
ולכן מתקיים תנאי הרציפות,
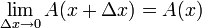 .
.

סעיף ב'
שלום