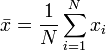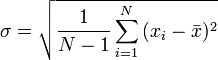חישובי שגיאה
בעבודה ניסיונית אנו מבצעים מדידות על מנת לדעת ולבחון גודל פיזיקאלי מסויים. במצב אידיאלי הגודל הנמדד יהיה זהה לערך המחושב. אך בפועל, בכל מדידה ישנה שגיאה. השגיאות יכולות לנבוע מרמת דיוקו של מכשיר המדידה, מהאדם המודד ומעוד גורמים חיצוניים המטים את המדידות. ניתן לאמוד את גודלה של השגיאה כדי לבסס את מהימנותה של המדידה.
שגיאות המדידה הן בחלקן שיטתיות ובחלקן אקראיות (אף כי לעתים אין אבחנה זו ברורה די צרכה). השגיאות השיטתיות נובעות מגורמים קבועים, ובהתאם לכך הן חוזרות ונשנות באותה מגמה עצמה. אם בתהליך השקילה של גוף משתמשים במשקולת מזויפת תהיה תוצאת השקילה מוטעית. דרך מקובלת לקיזוז שגיאה שיטתית היא לבצע מדידה דיפרנציאלית, כלומר, אם בשתי מדידות קיימת אותה סטייה, אז ההפרש בין תוצאות המדידה שוה להפרש בין הערכים האמיתיים והשגיאה השיטתית מקוזזת.
השגיאות האקראיות נובעות, לעומת זאת, מגורמים הפועלים במגמות שונות: מגבלות הדיוק הטבעיות של מכשירי המדידה והאיש המודד, שינוים אקראיים בתנאיי המדידה וכו'. בהתאם לכך, אם נחזור על מדידה מסוימת פעמים אחדות, תהיינה תוצאותיה שונות במקצת זו מזו. בהעדר שגיאות שיטתיות, נוכל להניח, כי שגיאות המדידה בשני הכיוונים דומות, ומשום כך משקף הממוצע החשבוני של התוצאות את התוצאה האמיתית באופן הטוב ביותר.
באופן איכותי אפשר לאמר ששגיאה אקראית נובעת בהכרח מגורם המשתנה מהר ביחס לזמן הכולל של הניסוי, לכן משתנה ממדידה למדידה, וגורם לפיזור בתוצאות. (דוגמא: חיכוך שמשתנה ממדידה למדידה, שינויי לחץ אוויר וטמפרטורה). שגיאה שיטתית היא כזו אשר נשארת קבועה בזמן הניסיון וגורמת להזזה של כל התוצאות בערך קבוע, או הכפלה בגורם קבוע. (דוגמא: שעון שהולך לאט מדי, כיוון שכך מכוון המנגנון שלו).
קיימים שני סוגים עקריים של שגיאות אקראיות: שגיאות מכשיר ושגיאות סטטיסטיות.
תוכן עניינים
הערכת שגיאת מכשיר
את שגיאת המכשיר נעריך ע"י רגישות המכשיר. רגישות המכשיר היא המרחק בין השנתות הרגישות ביותר. לדוגמא, רגישות סרגל המחולק למילימטרים היא מילימטר, כלומר לא ניתן למדוד באמצעות הסרגל מרחקים
הקטנים ממילימטר. כאשר אנו מודדים אורך באמצעות הסרגל, תוצאת המדידה תהיה הערך של השנתה הקרובה ביותר לגודל הנמדד, כלומר אנו מעגלים את תוצאת המדידה ומזניחים במדידה זו מרחקים הקטנים ממחצית המילימטר ולכן ישנה שגיאה אקראית של מחצית המילימטר בכל קריאה. מדידת אורך מתבצעת למעשה ע"י קריאת הערך בשתי נקודות ולכן הערכת השגיאה הכוללת במדידת האורך תהיה של מילימטר אחד כלומר רגישות הסרגל.
במכשיר מדידה דיגיטלי, רגישות המכשיר היא הגודל אותו מייצגת הסיפרה הימנית ביותר בתצוגת המכשיר, אך לעתים מכשיר המדידה עצמו עלול להיות לא מדויק. במכשירי מדידה דיגיטליים מספק היצרן בדרך כלל הערכה של שגיאת המכשיר, הערכה זו נתונה באחוזים. לדוגמא: במדידת מתח באמצעות מד-מתח דיגיטלי נמדדה התוצאה 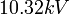 . רגישות המכשיר היא הספרה הימנית, כלומר
. רגישות המכשיר היא הספרה הימנית, כלומר 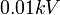 , ואילו בהוראות היצרן מופיע
כי שגיאת המכשיר בסקלת מדידה זו היא של
, ואילו בהוראות היצרן מופיע
כי שגיאת המכשיר בסקלת מדידה זו היא של 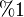 , כלומר במדידה זו תיתכן שגיאה של
, כלומר במדידה זו תיתכן שגיאה של 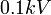 . במקרה זה רגישות המכשיר זניחה, והערכת השגיאה תהיה של
. במקרה זה רגישות המכשיר זניחה, והערכת השגיאה תהיה של 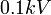 . כאשר מבצעים מספר מדידות של אותו גודל נמדד, נעריך את שגיאת המכשיר כשגיאה המקסימאלית מבין כל המדידות.
. כאשר מבצעים מספר מדידות של אותו גודל נמדד, נעריך את שגיאת המכשיר כשגיאה המקסימאלית מבין כל המדידות.
הערכת שגיאה סטטיסטית
על מנת להעריך את השגיאה הסטטיסטית יש לבצע מספר מדידות של הערך הנמדד. אם השגיאה הסטטיסטית גדולה מרגישות המכשיר, נקבל בכל מדידה ערך שונה, למרות שצורת המדידה היא קבועה בכל המדידות. לדוגמא: זמן מחזור של מטוטלת – מדידה בעזרת שעון-עצר. מתקבלות תוצאות שונות אחת מהשניה ויכולות להיות לכך כמה סיבות. למשל, פילוג במדידת הזמן (תלוי במהירות התגובה של המודד) , כושר דיוק לא מספיק של השעון, שינוי בזמן המחזור בין מדידה למדידה כאשר הטמפרטורה ולכן האורך של המטוטלת משתנה. נניח שאיננו מנתחים את סיבת ההבדלים בין הערכים הנמדדים אלא נגדיר גדלים אשר מאפיינים את קבוצת התוצאות, בעיקר מבחינת גודל השגיאה. אם נחזור על המדידה פעמים רבות נראה שתוצאות המדידה מתפלגות בהתפלגות נורמלית, ראו איור.

התפלגות נורמלית מאופיינת על ידי שני פרמטרים: התוחלת, 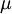 וסטיית התקן, עיבוד הנוסחה נכשל (שגיאת לקסינג): σ
. הערכים מפוזרים בצורה סימטרית מסביב לתוחלת, כך ש-
וסטיית התקן, עיבוד הנוסחה נכשל (שגיאת לקסינג): σ
. הערכים מפוזרים בצורה סימטרית מסביב לתוחלת, כך ש- 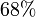 מהערכים נמצאים בתחום בין עיבוד הנוסחה נכשל (שגיאת לקסינג): μ+σ
מהערכים נמצאים בתחום בין עיבוד הנוסחה נכשל (שגיאת לקסינג): μ+σ
ל- עיבוד הנוסחה נכשל (שגיאת לקסינג): μ-σ . ערך התוחלת מייצג בצורה טובה את הערך האמיתי של הגודל הנמדד.
במציאות אנחנו מבצעים מספר סופי, N, של מדידות ולכן ערך התוחלת יוערך ע"י חישוב הממוצע החשבוני של תוצאות המדידה:
את סטיית התקן של ההתפלגות נעריך ע"י סטיית התקן של המדידות :
השגיאה הסטטיסטית המקסימאלית תהיה 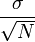 .
.
השגיאה הכוללת משלבת בתוכה את שני סוגי השגיאות האקראיות, שגיאת המכשיר, 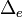 , והסטטיסטית, כך שהיא תוגדר להיות:
, והסטטיסטית, כך שהיא תוגדר להיות:
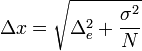
דוגמא: בניסוי שבו נשקלה מסה מסוימת 5 פעמים, התקבלו מדידות ממשקל דיגטלי עם רגישות של 0.1 גרם: 8.1, 8.3, 7.8, 7.5, 8, התוצאות בגרמים.
נחשב את הממוצע: 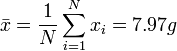
נחשב את סטיית התקן: 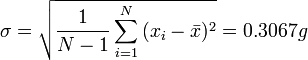
השגיאה הסטטיסטית תהיה: 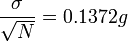 .
.
והשגיאה הכוללת:
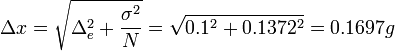
רישום התוצאות
כאשר השגיאה שיצאה מהחישובים מדייקת דיוק גדול יותר משגיאת המדידה, נעגל את השגיאה לשתי הספרות המשמעותיות ביותר, כלומר השמאליות ביותר השונות מ- . בדוגמא שלנו נאמר כי השגיאה ב-mks תהיה
. בדוגמא שלנו נאמר כי השגיאה ב-mks תהיה 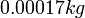 . ברור שהגודל הנמדד יוצג בניקוי דיוק הגבוה מזה של השגיאה, כיוון שאין משמעות לגודל של
. ברור שהגודל הנמדד יוצג בניקוי דיוק הגבוה מזה של השגיאה, כיוון שאין משמעות לגודל של 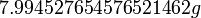 כאשר שגיאת מדידה היא
כאשר שגיאת מדידה היא 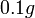 (גם אם כך התקבל במחשבון...)
(גם אם כך התקבל במחשבון...)
חישובי שגיאה של גדלים עקיפים
בסעיפים הקודמים דיברנו על השיטות להערכת שגיאה של גדלים הנמדדים ישירות באמצעות מכשירי המדידה. לדוגמה, אורך הנמדד בסרגל או זמן הנמדד באמצעות שעון הם גדלים הנמדדים ישירות. לעתים קרובות אנו מעוניינים לא רק בגדלים הנמדדים עצמם, אלה גם בגדלים עקיפים שהם פונקציות של הגדלים הנמדדים ישירות. לדוגמא: אנו מודדים זווית בעזרת מד-זווית, אולם לצורך חישובים כלשהם אנו מעוניינים בסינוס של הזווית ולא בזווית עצמה. אנו מעוניינים למדוד שטח של מלבן, לשם כך אנו מודדים בסרגל את אורכו ורוחבו, ומכפילים אותם זה בזה. כאן, השטח הוא פונקציה (מכפלה) של האורך והרוחב. מכיוון שהגודל העקיף הוא פונקציה של הגדלים הנמדדים ישירות, ברור ששגיאה במדידת הגדלים הישירים תגרום לשגיאה בהערכת הגודל העקיף. בניסוח מתמטי , אנו מעוניינים לענות על השאלה: אם  הוא פונקציה מסוימת של גדלים שונים
הוא פונקציה מסוימת של גדלים שונים 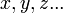 ושגיאותיהם של הגדלים האלו הן
ושגיאותיהם של הגדלים האלו הן 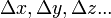 , מהי השגיאה
, מהי השגיאה 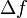 ?
?
נניח שידועות לנו צורת הפונקציה 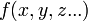 , תוצאות המדידה
, תוצאות המדידה 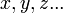 ושגיאותיהן
ושגיאותיהן 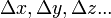 . כדי לענות על שאלתנו עכשיו, ננסה לענות קודם על שאלה פשוטה יותר: נניח שרק
. כדי לענות על שאלתנו עכשיו, ננסה לענות קודם על שאלה פשוטה יותר: נניח שרק  משתנה ב-
משתנה ב- 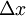 , וכל שאר הגדלים
, וכל שאר הגדלים 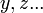 נשארים קבועים, מהו השינוי ב-
נשארים קבועים, מהו השינוי ב-  הנגרם רק על-ידי השינוי ב-
הנגרם רק על-ידי השינוי ב-  ? (נסמן שינוי זה של
? (נסמן שינוי זה של  ב-
ב- 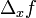 ). כיוון שהגדלים
). כיוון שהגדלים 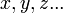 אינם משתנים, אפשר להתייחס ל-
אינם משתנים, אפשר להתייחס ל-  כאילו היא פונקציה של
כאילו היא פונקציה של  , ולגזור אותה: נגזרת כזו, המתקבלת כתוצאה מגזירת פונקציה רבת-משתנים ביחס למשתנה אחד בלבד, כאשר מתייחס לכל שאר המשתנים כאילו היו קבועים, נקראת בשם נגזרת חלקית ומסומנת כך:
, ולגזור אותה: נגזרת כזו, המתקבלת כתוצאה מגזירת פונקציה רבת-משתנים ביחס למשתנה אחד בלבד, כאשר מתייחס לכל שאר המשתנים כאילו היו קבועים, נקראת בשם נגזרת חלקית ומסומנת כך: 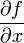 .
.
כלומר השינוי בפונקציה  כתוצאה משגיאה של
כתוצאה משגיאה של 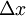 במשתנה
במשתנה  , תהיה:
, תהיה:
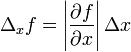
ובאופן דומה: 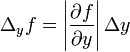 ,
, 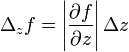 וכו'.
וכו'.
לאחר שחישבנו את גודלם של השינויים ...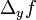 ,
,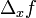 (נכנה שינוים אלו בשם השגיאות החלקיות), נחזור לשאלה המקורית: מהו השינוי
(נכנה שינוים אלו בשם השגיאות החלקיות), נחזור לשאלה המקורית: מהו השינוי 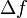 הנגרם בגלל השינויים בכל הגדלים
הנגרם בגלל השינויים בכל הגדלים 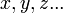 ? אנו מניחים שהשגיאות החלקיות קטנות, ולכן אפשר להתעלם מהשפעתו של השינוי של אחד מהגדלים האלו על גודלן של השגיאות על גודלן של השגיאות החלקיות הנגרמות בגלל שאר הגדלים. לכן, השינוי של כל אחד מהגדלים
? אנו מניחים שהשגיאות החלקיות קטנות, ולכן אפשר להתעלם מהשפעתו של השינוי של אחד מהגדלים האלו על גודלן של השגיאות על גודלן של השגיאות החלקיות הנגרמות בגלל שאר הגדלים. לכן, השינוי של כל אחד מהגדלים 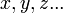 יסיט את ערכה של הפונקציה
יסיט את ערכה של הפונקציה  כלפי מעלה או מטה בכמות השווה לגודלה של השגיאה החלקית המתאימה שחישבנו.
כלפי מעלה או מטה בכמות השווה לגודלה של השגיאה החלקית המתאימה שחישבנו.
במקרה הגרוע ביותר, שבו כל השגיאות החלקיות מסיטות את  לאותו כיוון, יהיה גודל השינוי של
לאותו כיוון, יהיה גודל השינוי של  שווה לסכום כל השגיאות החלקיות, כלומר:
שווה לסכום כל השגיאות החלקיות, כלומר:
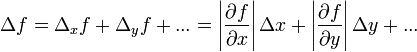
אולם הערכה זו היא פסימית מדי. ראשית, הערכות השגיאה שלנו הן מקסימליות, וברוב המקרים תהיה השגיאה האמיתית במדידת  קטנה מהערכה
קטנה מהערכה 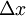 . הסיכוי לכך שכל השגיאות יקבלו בבת-אחת את ערכן המקסימלי הוא קטן. שנית, מכיוון שאנו עוסקים בשגיאות אקראיות, חלק מהשגיאות של הגדלים הנמדדים ישירות יגדילו את ערכו של
. הסיכוי לכך שכל השגיאות יקבלו בבת-אחת את ערכן המקסימלי הוא קטן. שנית, מכיוון שאנו עוסקים בשגיאות אקראיות, חלק מהשגיאות של הגדלים הנמדדים ישירות יגדילו את ערכו של  ואחרות יקטינו אותו. לכן, הערכת השגיאה הכללית כסכום השגיאות היא מוגזמת. הערך הסביר יותר של
ואחרות יקטינו אותו. לכן, הערכת השגיאה הכללית כסכום השגיאות היא מוגזמת. הערך הסביר יותר של 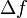 הוא שורש סכום הריבועים של השגיאות החלקיות, כלומר:
הוא שורש סכום הריבועים של השגיאות החלקיות, כלומר:
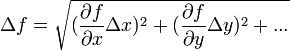
(ויתרנו על הערך המוחלט משום שהעלאה בריבוע מבטלת את הסימן).
במעבדה נשתמש בנוסחה זו.