חתכי דדקינד
הקדמה
- אנחנו מעוניינים שבמערכת המספרים שלנו יהיה פתרון למשוואה [math]\displaystyle{ x^2=2 }[/math] (שורש שתיים).
- הרי אחרת, מה המרחק מהנקודה [math]\displaystyle{ (1,1) }[/math] לראשית הצירים [math]\displaystyle{ (0,0) }[/math]?
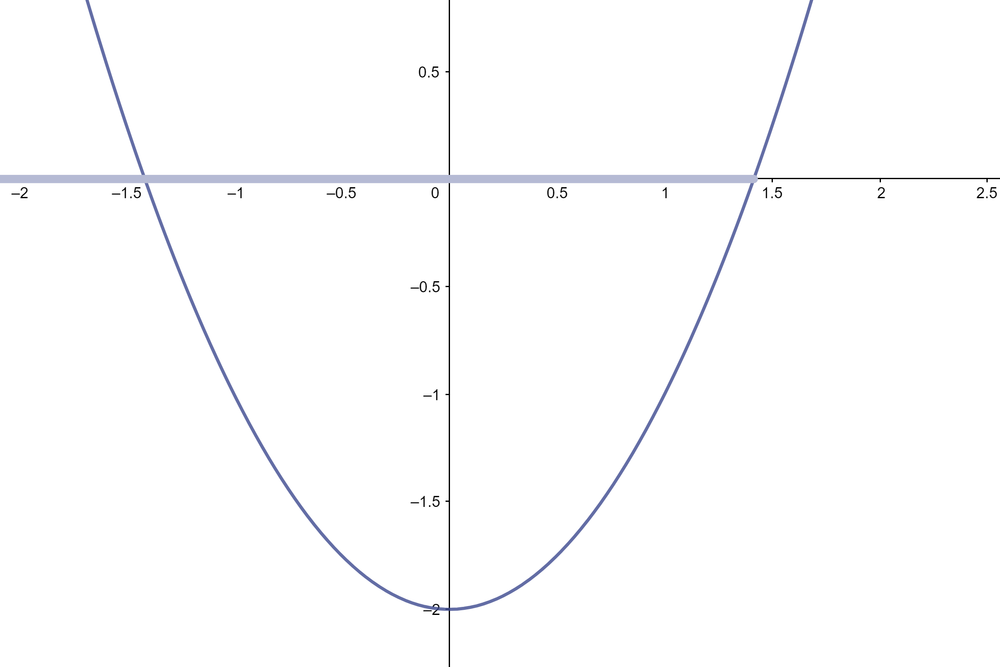
- האם ייתכן שהפרבולה [math]\displaystyle{ y=x^2-2 }[/math] עולה מהנקודה [math]\displaystyle{ (0,-2) }[/math] אל הנקודה [math]\displaystyle{ (2,2) }[/math] בלי לחתוך את ציר האיקס?
- כיוון שאין פתרון למשוואה זו בשדה הרציונאליים, אנחנו רוצים לבנות את שדה הממשיים.
- כיצד ניתן לתאר את נקודת החיתוך החיובית של הפרבולה [math]\displaystyle{ y=x^2-2 }[/math] עם ציר האיקס באמצעות המספרים הרציונאליים אם כך?
(נבנה באמצעות גאוגברה.)
- ובכן, ניתן לומר שציר המספרים מתחלק לשניים - לפני שורש שתיים ואחרי שורש שתיים.
- כלומר, אולי אנחנו יכולים לייצג את נקודת החיתוך על ידי אוסף הנקודות שקטנות ממנה [math]\displaystyle{ \left\{x\in\mathbb{Q}| x\lt 0 \vee x^2 \lt 2\right\} }[/math], זו הקרן באיור.
- הרעיון הזה של חיתוך ציר הרציונאליים סביב נקודה בלתי קיימת הוליד את חתכי דדקינד.
חתכי דדקינד
- הגדרה: חתך דדקינד הוא קבוצה [math]\displaystyle{ A\subseteq\mathbb{Q} }[/math] המקיימת:
- [math]\displaystyle{ A\neq\emptyset }[/math]
- [math]\displaystyle{ A }[/math] חסומה מלעיל.
- לכל [math]\displaystyle{ m\in\mathbb{Q} }[/math] מתקיים כי [math]\displaystyle{ m\notin A }[/math] אם ורק אם [math]\displaystyle{ m }[/math] חסם מלעיל של [math]\displaystyle{ A }[/math]
- הערות ותזכורות:
- חסם מלעיל של קבוצה הוא מספר שגדול יותר מכל איברי הקבוצה.
- בחתך דדקינד אין מספר גדול ביותר, אחרת זה היה חסם מלעיל ששיך לקבוצה. זה משול לחצי האבוקדו ללא הגרעין.
- בחתך המייצג מספר שאינו רציונאלי, כמו שורש שתיים, גם במשלים של החתך אין מספר קטן ביותר, זה משול לשני חצאי אבוקדו ללא גרעין כלל.
- אם מספר שייך לחתך, בוודאי כל מספר נמוך ממנו שייך לחתך הרי לא ייתכן שמספר נמוך ממנו הוא חסם מלעיל.
- הקרן באיור לעיל היא חתך דדקינד שתפקידו להגדיר את שורש שתיים.
- כיצד ניתן להתייחס לקבוצות כאלה בתור מספרים?
- עלינו להגיד פעולות בין חתכי דדקינד ולהוכיח שמדובר בשדה.
- כאשר נגדיר את הפעולות, נזכור שמטרתינו היא להגדיר את הנקודות "החסרות" על הציר.
חיבור חתכי דדקינד
- יהיו שתי חתכים [math]\displaystyle{ A,B }[/math], נגדיר את החיבור:
- [math]\displaystyle{ A+B=\left\{a+b|a\in A,b\in B\right\} }[/math]
- החיבור הוא חתך דדקינד בעצמו:
- כיוון שA,B אינן ריקות גם A+B אינה ריקה.
- סכום חסמי מלעיל של A וB חוסם את A+B.
- יהי [math]\displaystyle{ a+b\in A+B }[/math], כיוון שאיברי החתכים אינם חסמי מלעיל, קיימים [math]\displaystyle{ a\lt c\in A }[/math] וכן [math]\displaystyle{ b\lt d\in B }[/math] ולכן [math]\displaystyle{ a+b\lt c+d\in A+B }[/math] ו[math]\displaystyle{ a+b }[/math] אינו חסם מלעיל של [math]\displaystyle{ A+B }[/math]
- יהי [math]\displaystyle{ m\in\mathbb{Q} }[/math] שאינו חסם מלעיל של [math]\displaystyle{ A+B }[/math], לכן קיימים [math]\displaystyle{ m\lt a+b\in A+B }[/math]. כעת [math]\displaystyle{ m-a\lt b }[/math] כלומר [math]\displaystyle{ m-a }[/math] אינו חסם מלעיל של B ולכן שייך לקבוצה. סה"כ [math]\displaystyle{ m=a+(m-a)\in A+B }[/math].
חתך האפס
- נגדיר את חתך האפס:
- [math]\displaystyle{ 0_D=\left\{x\in\mathbb{Q}|x\lt 0\right\} }[/math]
- נוכיח כי חתך האפס נייטרלי לחיבור:
- יהי חתך דדקינד [math]\displaystyle{ A }[/math] צריך להוכיח כי [math]\displaystyle{ A+0_D=A }[/math]
- נבצע הכלה דו כיוונית. בכיוון הראשון:
- יהי [math]\displaystyle{ x=a+h\in A+0_D }[/math] צריך להוכיח כי [math]\displaystyle{ x\in A }[/math]
- כיוון ש [math]\displaystyle{ h\in 0_D }[/math] נובע לפי ההגדרה כי [math]\displaystyle{ h\lt 0 }[/math] ולכן [math]\displaystyle{ a+h\lt a }[/math]
- לכן [math]\displaystyle{ x=a+h }[/math] אינו חסם מלעיל של [math]\displaystyle{ A }[/math] ולכן [math]\displaystyle{ x\in A }[/math]
- בכיוון השני:
- יהי [math]\displaystyle{ a\in A }[/math] צריך להוכיח כי [math]\displaystyle{ a\in A+0_D }[/math]
- אמרנו כי בחתך דדקינד אין איבר גדול ביותר, ולכן קיים [math]\displaystyle{ a\lt b\in A }[/math]
- כיוון ש [math]\displaystyle{ a-b\lt 0 }[/math] נובע כי [math]\displaystyle{ a-b\in 0_D }[/math]
- סה"כ [math]\displaystyle{ a=b+(a-b)\in A+0_D }[/math] כפי שרצינו.
נגדי
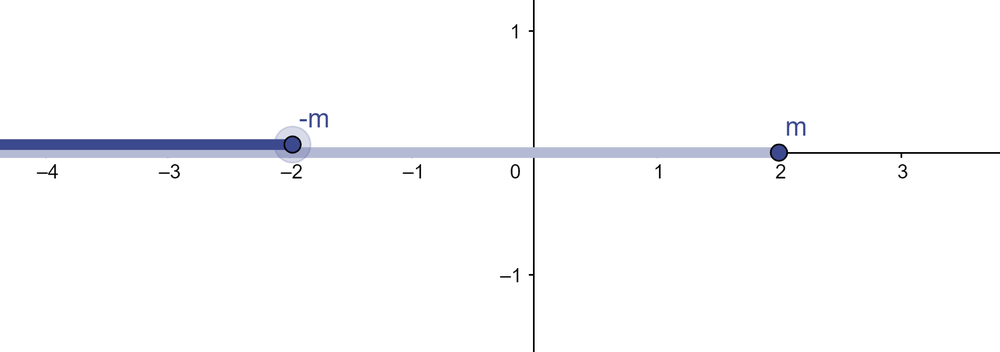
- יהי חתך A, נגדיר את הנגדי:
- [math]\displaystyle{ -A=\left\{x\in\mathbb{Q}|\exists m\notin A:x\lt -m\right\} }[/math]
- לדוגמא [math]\displaystyle{ -\left\{x\in\mathbb{Q}|x\lt 2\right\}=\left\{x\in\mathbb{Q}|x\lt -2\right\} }[/math]
- הנגדי הוא חתך דדקינד בעצמו:
- הנגדי לא ריק:
- כיוון שA חסומה מלעיל יש לה חסם, וכל המספרים שקטנים ממינוס החסם שייכים לנגדי, ולכן [math]\displaystyle{ -A\neq\emptyset }[/math]
- הנגדי חסום מלעיל:
- יהי [math]\displaystyle{ a\in A }[/math] לכן לכל [math]\displaystyle{ m\notin A }[/math] מתקיים כי [math]\displaystyle{ a\lt m }[/math] ולכן [math]\displaystyle{ -m\lt -a }[/math]
- לכל [math]\displaystyle{ x\in -A }[/math] קיים [math]\displaystyle{ m\notin A }[/math] כך ש [math]\displaystyle{ x\lt -m }[/math] ולכן [math]\displaystyle{ x\lt -a }[/math]
- בעצם הנגדי של כל איבר בA הוא חסם מלעיל של [math]\displaystyle{ -A }[/math].
- כל איבר בנגדי אינו חסם מלעיל:
- לכל איבר בנגדי [math]\displaystyle{ x\lt -m }[/math] לכן אמצע הקטע בין [math]\displaystyle{ x,-m }[/math] גדול מ[math]\displaystyle{ x }[/math] וקטן מ[math]\displaystyle{ -m }[/math] ולכן שייך לנגדי [math]\displaystyle{ -A }[/math] ולכן [math]\displaystyle{ x }[/math] אינו חסם מלעיל.
- אם איבר אינו חסם מלעיל, הוא שייך לנגדי:
- נניח [math]\displaystyle{ y }[/math] אינו חסם מלעיל של [math]\displaystyle{ -A }[/math] לכן קיים [math]\displaystyle{ y\lt x\in -A }[/math] ולכן קיים [math]\displaystyle{ m\notin A }[/math] כך ש [math]\displaystyle{ y\lt x\lt -m }[/math] ולכן [math]\displaystyle{ y\in -A }[/math]
- הנגדי לא ריק:
הוכחה שאכן מדובר באיבר נגדי
- יהי חתך [math]\displaystyle{ A }[/math] צריך להוכיח כי [math]\displaystyle{ A+(-A)=0_D }[/math]
- נבצע הכלה דו כיוונית
- בכיוון ראשון:
- יהי [math]\displaystyle{ x+y\in (A+(-A)) }[/math].
- כיוון ש[math]\displaystyle{ y\in (-A) }[/math] קיים [math]\displaystyle{ m\not\in A }[/math] כך ש [math]\displaystyle{ y\lt -m }[/math]
- לכן [math]\displaystyle{ x+y\lt m+y\lt 0 }[/math]
- לכן [math]\displaystyle{ x+y\in 0_D }[/math]
- בכיוון שני:
- יהי [math]\displaystyle{ t\in 0_D }[/math] כלומר [math]\displaystyle{ t\lt 0 }[/math]
- רוצים למצוא [math]\displaystyle{ a\in A, b\in (-A) }[/math] כך ש [math]\displaystyle{ a+b=t }[/math]
- נבחר [math]\displaystyle{ m\not\in A }[/math] כך ש[math]\displaystyle{ m+\frac{t}{2}\in A }[/math]
- מדוע זה אפשרי? כי אם [math]\displaystyle{ m+\frac{t}{2}\not\in A }[/math] אז זה חסם, ואפשר להוסיף לו [math]\displaystyle{ \frac{t}{2} }[/math] שזה מספר שלילי. אחרי מספיק פעמים נהיה קטנים מאיבר בקבוצה
- כעת [math]\displaystyle{ -m+\frac{t}{2}\lt -m }[/math] ולכן [math]\displaystyle{ -m+\frac{t}{2}\in (-A) }[/math].
- סה"כ [math]\displaystyle{ t=(m+\frac{t}{2})+(-m+\frac{t}{2})\in A+(-A) }[/math]
יחס סדר
- יחס ההכלה הוא יחס סדר לינארי (מלא) על קבוצת חתכי דדקינד
- הוכחה:
- יהיו שני חתכים A,B.
- אם קיים [math]\displaystyle{ m\notin A }[/math] חסם מלעיל של A כך ש[math]\displaystyle{ m\in B }[/math] אזי כל איבר של A אינו חסם מלעיל של B ולכן שייך לB, כלומר [math]\displaystyle{ A\subseteq B }[/math]
- אחרת, לכל [math]\displaystyle{ m\notin A }[/math] מתקיים כי [math]\displaystyle{ m\notin B }[/math]. כלומר [math]\displaystyle{ \overline{A}\subseteq\overline{B} }[/math] ולכן [math]\displaystyle{ B\subseteq A }[/math]
- נגדיר את החתכים החיוביים להיות כל החתכים A כך ש[math]\displaystyle{ 0_D \lt A }[/math] ונגדיר את החתכים השליליים על ידי [math]\displaystyle{ 0_D \gt A }[/math]
- טענה: [math]\displaystyle{ A\geq 0_D }[/math] אם ורק אם [math]\displaystyle{ -A\leq 0_D }[/math]
- הוכחה:
- ראשית נניח כי [math]\displaystyle{ A\geq 0_D }[/math]
- כלומר בעצם [math]\displaystyle{ 0_D\subseteq A }[/math] ולכן לכל חסם מלעיל [math]\displaystyle{ m\notin A }[/math] מתקיים כי [math]\displaystyle{ 0\leq m }[/math].
- לכן לכל [math]\displaystyle{ x\in -A }[/math] מתקיים כי [math]\displaystyle{ x\lt -m\lt 0 }[/math]
- כלומר כל האיברים ב[math]\displaystyle{ -A }[/math] שליליים, ולכן [math]\displaystyle{ -A\subseteq 0_D }[/math] כלומר [math]\displaystyle{ -A\leq 0_D }[/math]
- בכיוון ההפוך, נניח כי [math]\displaystyle{ -A\leq 0_D }[/math]
- לכן כל האיברים ב[math]\displaystyle{ -A }[/math] שליליים.
- אם קיים [math]\displaystyle{ 0\gt m\notin A }[/math] אזי [math]\displaystyle{ 0\lt -\frac{m}{2}\in -A }[/math] בסתירה.
- לכן כל המספרים השליליים שייכים לA, כלומר [math]\displaystyle{ 0_D\subseteq A }[/math] ולכן [math]\displaystyle{ A\geq 0_D }[/math]
- ראשית נניח כי [math]\displaystyle{ A\geq 0_D }[/math]
כפל חתכי דדקינד
- יהיו שני חתכי דדקינד אי שליליים [math]\displaystyle{ 0_D\leq A,B }[/math], נגדיר את הכפל:
- [math]\displaystyle{ A\cdot B =\left\{x\cdot y|x\in A\setminus 0_D \wedge y\in B\setminus 0_D\right\}\cup 0_D }[/math]
- אם A שלילי, וB אי שלילי, נגדיר:
- [math]\displaystyle{ A\cdot B = - ((-A)\cdot B) }[/math]
- אם A אי שלילי, וB שלילי, נגדיר:
- [math]\displaystyle{ A\cdot B = - (A\cdot (-B)) }[/math]
- אם A,B שליליים נגדיר:
- [math]\displaystyle{ A\cdot B = (-A)\cdot (-B) }[/math]
הוכחה שהמכפלה נותנת חתך דדקינד
- יהיו שני חתכי דדקינד חיוביים [math]\displaystyle{ 0_D\lt A,B }[/math]
- ברור שהמכפלה לא ריקה כיוון ש [math]\displaystyle{ 0_D\subseteq A\cdot B }[/math]
- כיוון שA,B חתכי דדקינד מדובר בקבוצות חסומות, אז קיימים חסמי מלעיל [math]\displaystyle{ m_A,m_B }[/math] בהתאמה.
- לכל [math]\displaystyle{ xy\in AB }[/math] מתקיים כי [math]\displaystyle{ x\lt m_A,y\lt m_B }[/math] ולכן [math]\displaystyle{ xy\lt m_A\cdot m_B }[/math]. זה נכון כי החסמים חיוביים, כי מדובר בחתכים חיוביים.
- אם [math]\displaystyle{ t\in AB }[/math] צ"ל כי [math]\displaystyle{ t }[/math] אינו חסם מלעיל של [math]\displaystyle{ AB }[/math].
- אם [math]\displaystyle{ t\leq 0 }[/math] ברור שאינו חסם מלעיל של [math]\displaystyle{ AB }[/math] כיוון שיש בקבוצה מספרים חיוביים.
- לכן [math]\displaystyle{ t=xy\in AB }[/math].
- כיוון ש[math]\displaystyle{ x }[/math] אינו חסם מלעיל של [math]\displaystyle{ A }[/math] קיים [math]\displaystyle{ x\lt z\in A }[/math] ולכן [math]\displaystyle{ xy\lt zy\in A }[/math] בסתירה.
- אם [math]\displaystyle{ t\not\in AB }[/math] צ"ל כי [math]\displaystyle{ t }[/math] חסם מלעיל.
- נב"ש כי [math]\displaystyle{ t }[/math] אינו חסם מלעיל, לכן יש בקבוצה איבר גדול ממנו.
- כיוון ש [math]\displaystyle{ t\not\in AB }[/math] נובע כי [math]\displaystyle{ t\gt 0 }[/math], ולכן האיבר שגדול ממנו הוא מהצורה [math]\displaystyle{ t\lt xy }[/math].
- לכן [math]\displaystyle{ \frac{t}{y}\lt x }[/math], נבחר [math]\displaystyle{ x_1 =\frac{t}{y}\lt x }[/math].
- כיוון ש[math]\displaystyle{ x_1 \lt x }[/math] נובע כי [math]\displaystyle{ x_1 \in A }[/math].
- לכן [math]\displaystyle{ t=x_1 y\in A\cdot B }[/math] בסתירה.
- אם אחד החתכים הוא [math]\displaystyle{ 0_D }[/math] קל להוכיח כי מכפלתם היא [math]\displaystyle{ 0_D }[/math] ולכן מהווה חתך.
חתך היחידה
- נגדיר את חתך היחידה, בהמשך נוכיח שהוא נייטרלי לכפל.
- [math]\displaystyle{ 1_D=\{x\in\mathbb{Q}|x\lt 1\} }[/math]
הופכי
- אם A חיובי נגדיר את ההופכי שלו להיות
- [math]\displaystyle{ A^{-1}=\{x\in\mathbb{Q}|\exists m\not\in A:x\lt \frac{1}{m}\} }[/math]
- אם A שלילי נגדיר את ההופכי שלו להיות
- [math]\displaystyle{ A^{-1}=-(-A)^{-1} }[/math]
הוכחה שההופכי הוא חתך דדקינד
- נניח A חיובי, ויהי [math]\displaystyle{ 0\lt a\in A }[/math].
- לכל חסם [math]\displaystyle{ m\not\in A }[/math] מתקיים כי [math]\displaystyle{ a\lt m }[/math]
- לפיכך [math]\displaystyle{ \frac{1}{m}\lt \frac{1}{a} }[/math]
- לכן [math]\displaystyle{ \frac{1}{a} }[/math] הוא חסם מלעיל של [math]\displaystyle{ A^{-1} }[/math]
- ברור כי [math]\displaystyle{ A^{-1} }[/math] אינו ריק, כי לA יש חסם מלעיל, וכל מספר שקטן ממהופכי שלו שייך ל[math]\displaystyle{ A^{-1} }[/math]
- נוכיח כי כל מספר ב[math]\displaystyle{ A^{-1} }[/math] אינו חסם מלעיל.
- אם [math]\displaystyle{ x\lt \frac{1}{m}\in A^{-1} }[/math] אז גם אמצע הקטע [math]\displaystyle{ x\lt y\lt \frac{1}{m}\in A^{-1} }[/math]
- לבסוף, יהי [math]\displaystyle{ x }[/math] שאינו חסם מלעיל של [math]\displaystyle{ A^{-1} }[/math]
- לכן [math]\displaystyle{ x\lt y\in A^{-1} }[/math]
- והרי קיים חסם של A כך ש [math]\displaystyle{ y\lt \frac{1}{m} }[/math]
- ולכן גם [math]\displaystyle{ x\lt \frac{1}{m} }[/math] ולכן [math]\displaystyle{ x\in A^{-1} }[/math]
הוכחה שאכן מדובר בהופכי
- יהי A חיובי, נוכיח כי [math]\displaystyle{ A^{-1}A=1 }[/math]
- ראשית, נוכיח כי [math]\displaystyle{ A^{-1}A\leq 1 }[/math]
- יהי [math]\displaystyle{ 0\lt xa\in A^{-1}A }[/math]
- [math]\displaystyle{ x\in A^{-1} }[/math], לכן קיים חסם מלעיל [math]\displaystyle{ m\not\in A }[/math] כך ש [math]\displaystyle{ x\lt \frac{1}{m} }[/math]
- כמובן ש [math]\displaystyle{ a\lt m }[/math]
- ביחד [math]\displaystyle{ xa\lt \frac{1}{m}\cdot m=1 }[/math].
- כעת נוכיח כי [math]\displaystyle{ A^{-1}A\geq 1 }[/math]
- צ"ל כי אפשר לבחור איבר [math]\displaystyle{ xa\in A^{-1}A }[/math] הקרוב ל1 כרצוננו.
- נבחר [math]\displaystyle{ 0\lt a\in A, m\not\in A }[/math] כך ש [math]\displaystyle{ a,m }[/math] קרובים כרצוננו (אפשרי כי מכל זוג של מספר וחסם אפשר להחליף אחד מהם באמצע הקטע).
- נבחר [math]\displaystyle{ x\lt \frac{1}{m} }[/math] כך ש[math]\displaystyle{ x,\frac{1}{m} }[/math] קרובים כרצוננו.
- סה"כ [math]\displaystyle{ 1-xa=m\cdot \frac{1}{m}-a\cdot \frac{1}{m}+a\cdot \frac{1}{m}-ax=\frac{1}{m}(m-a)+a(\frac{1}{m}-x) }[/math]
- כיוון שקבוצת החסמים [math]\displaystyle{ m }[/math] חסומה מלמטה ע"י איברי חיובי מA, וכיוון שאפשר לקרב את [math]\displaystyle{ m-a }[/math] כרצוננו לאפס, סה"כ אפשר לקרב את ההפרש הזה כרצוננו לאפס, כפי שרצינו.
- לבסוף, אם [math]\displaystyle{ A }[/math] שלילי, [math]\displaystyle{ A^{-1}=-(-A)^{-1} }[/math]
- לכן [math]\displaystyle{ A^{-1}A=-(-A)^{-1}\cdot A = (-A)^{-1}\cdot (-A)=1 }[/math]
- המעבר האחרון הוא לפי הגדרת הכפל עבור חתכים שליליים.
שדה הממשיים
הגדרת המספרים הממשיים
- הגדרה: [math]\displaystyle{ \mathbb{R} }[/math] הוא קבוצת כל חתכי דדקינד.
שדה הממשיים הוא סדר סדור
- נוכיח שמדובר בשדה סדור ביחס לפעולות החיבור והכפל ויחס הסדר שהגדרנו לעיל.
הוכחה
תכונות השדה
- סגירות - הוכחנו לעיל שסכום חתכים הוא חתך, וכן כפל חתכים הוא חתך
- חילופיות - טריוויאלי מחילופיות החיבור והכפל ברציונאליים.
- אסוציאטיביות - טריוויאלי מאסוציאטיביות החיבור והכפל ברציונאליים.
- נייטרלים - הגדרנו איברים נייטרלים לעיל ואפילו הוכחנו שהם אכן נייטרלים
- נגדיים - הגדרנו והוכחנו לעיל
- הופכיים - הגדרנו והוכחנו לעיל
- פילוג - נובע מפילוג הרציונאליים
תכונות שדה סדור
- איזוטוניות ביחס לסכום:
- יהיו חתכים A,B,C כך ש[math]\displaystyle{ A\leq B }[/math] צ"ל כי [math]\displaystyle{ A+C\leq B+C }[/math]
- נתון כי [math]\displaystyle{ A\subseteq B }[/math] צ"ל כי [math]\displaystyle{ A+C\subseteq B+C }[/math]
- יהי [math]\displaystyle{ a+c\in A+C }[/math], לכן [math]\displaystyle{ a\in B }[/math] ולכן [math]\displaystyle{ a+c\in B+C }[/math].
- יהיו זוג חתכים [math]\displaystyle{ A\leq B }[/math] ויהי חתך [math]\displaystyle{ C }[/math] חיובי. צ"ל כי [math]\displaystyle{ AC\leq BC }[/math]
- ראשית נניח כי A,B חתכים חיוביים
- יהי [math]\displaystyle{ 0\lt ac\in AC }[/math] כאשר [math]\displaystyle{ 0\lt a,c }[/math].
- כיוון ש [math]\displaystyle{ A\subseteq B }[/math] נובע כי [math]\displaystyle{ a\in B }[/math] ולכן [math]\displaystyle{ ac\in BC }[/math].
- כעת נניח כי A שלילי ואילו B חיובי (המצב ההפוך סותר את הנתונים)
- לפי הגדרת הכפל [math]\displaystyle{ AC=-((-A)C) }[/math] הוא חתך שלילי, ולכן בוודאי קטן מהחתך החיובי [math]\displaystyle{ BC }[/math]
- ראשית נניח כי A,B חתכים חיוביים
- לבסוף נניח כי A,B חתכים שליליים
- ראשית נוכיח טענת עזר: [math]\displaystyle{ A\leq B }[/math] אם ורק אם [math]\displaystyle{ -A\geq -B }[/math]
- בכיוון אחד, נתון כי [math]\displaystyle{ A\leq B }[/math] ורוצים להוכיח כי [math]\displaystyle{ -A\geq -B }[/math]
- יהי [math]\displaystyle{ x\in -B }[/math], כלומר קיים חסם [math]\displaystyle{ m\not\in B }[/math] כך ש [math]\displaystyle{ x\lt m }[/math]
- כיוון ש[math]\displaystyle{ A\leq B }[/math] נובע כי [math]\displaystyle{ m\not\in A }[/math] ולכן [math]\displaystyle{ x\in -A }[/math]
- בכיוון השני, נשתמש בכיוון הראשון ובעובדה כי [math]\displaystyle{ -(-A)=A }[/math]
- בכיוון אחד, נתון כי [math]\displaystyle{ A\leq B }[/math] ורוצים להוכיח כי [math]\displaystyle{ -A\geq -B }[/math]
- כעת נחזור להוכחה:
- מהנתון נובע כי [math]\displaystyle{ -A\geq -B }[/math]
- כבר הוכחנו עבור חתכים חיוביים כי נובע ש [math]\displaystyle{ (-A)C\geq (-B)C }[/math]
- לכן [math]\displaystyle{ -((-A)C)\leq -((-B)C) }[/math]
- כלומר הוכחנו [math]\displaystyle{ AC\leq BC }[/math]
שלמות הממשיים
- תהי [math]\displaystyle{ \emptyset\neq A\subseteq \mathbb{R} }[/math] קבוצה לא ריקה של מספרים ממשיים, וחסומה מלעיל (כלומר קיים [math]\displaystyle{ M\in\mathbb{R} }[/math] כך ש[math]\displaystyle{ \forall a\in A:a\leq M }[/math]. אזי קיים ל[math]\displaystyle{ A }[/math] חסם עליון ממשי.
הוכחה
- נסמן ב[math]\displaystyle{ S }[/math] את האיחוד הכללי של כל חתכי הדדקינד ששייכים ל[math]\displaystyle{ A }[/math], כלומר [math]\displaystyle{ S=\cup_{x\in A} x }[/math]
- נוכיח כי האיחוד הכללי של כל חתכי הדדקינד הוא גם חתך דדקינד.
- [math]\displaystyle{ S }[/math] אינה ריקה
- [math]\displaystyle{ A }[/math] אינה ריקה, ולכן קיים [math]\displaystyle{ x\in A }[/math].
- כיוון ש[math]\displaystyle{ x }[/math] חתך דדקינד הוא אינו ריק.
- [math]\displaystyle{ x\subseteq S }[/math] ולכן [math]\displaystyle{ S }[/math] אינה ריקה
- [math]\displaystyle{ S }[/math] חסומה:
- כיוון ש[math]\displaystyle{ M }[/math] חסם מלעיל של [math]\displaystyle{ A }[/math] לכל [math]\displaystyle{ x\in A }[/math] מתקיים כי [math]\displaystyle{ x\leq M }[/math]
- לפי יחס הסדר מתקיים כי [math]\displaystyle{ x\subseteq M }[/math].
- כיוון שלכל [math]\displaystyle{ x\in A }[/math] מתקיים כי [math]\displaystyle{ x\subseteq M }[/math] נובע כי גם [math]\displaystyle{ S\subseteq M }[/math].
- לכן [math]\displaystyle{ S }[/math] חסומה מלעיל.
- נוכיח כי [math]\displaystyle{ x\in S }[/math] אם ורק אם [math]\displaystyle{ x }[/math] אינו חסם מלעיל של [math]\displaystyle{ S }[/math]
- אם [math]\displaystyle{ x\in S }[/math] אזי [math]\displaystyle{ x\in D\in A }[/math]
- אם [math]\displaystyle{ x }[/math] חסם מלעיל של [math]\displaystyle{ S }[/math] אזי הוא בפרט חסם מלעיל של [math]\displaystyle{ D }[/math] בסתירה.
- מצד שני, אם [math]\displaystyle{ m }[/math] חסם מלעיל של [math]\displaystyle{ S }[/math] הוא בפרט חסם מלעיל של כל איברי [math]\displaystyle{ A }[/math] ולכן אינו שייך לאף אחד מאיברי [math]\displaystyle{ A }[/math] ולכן אינו שייך ל[math]\displaystyle{ S }[/math]
- [math]\displaystyle{ S }[/math] אינה ריקה
- ברור כי לכל [math]\displaystyle{ x\in A }[/math] מתקיים כי [math]\displaystyle{ x\leq S }[/math] כיוון ש[math]\displaystyle{ x\subseteq S }[/math] (כל קבוצה מוכלת באיחוד).
- נוכיח כי [math]\displaystyle{ S }[/math] הוא החסם העליון של [math]\displaystyle{ A }[/math].
- נב"ש כי קיים [math]\displaystyle{ T }[/math] חסם מלעיל של [math]\displaystyle{ A }[/math] כך ש [math]\displaystyle{ T\lt S }[/math].
- לכן קיים [math]\displaystyle{ x\in S\setminus T }[/math].
- לכן קיים [math]\displaystyle{ D\in A }[/math] כך ש [math]\displaystyle{ x\in D }[/math].
- לכן [math]\displaystyle{ D\not\subseteq T }[/math] בסתירה לכך ש[math]\displaystyle{ T }[/math] חסם מלעיל של [math]\displaystyle{ A }[/math]
ייצוג עשרוני של מספרים ממשיים
- ייצוג עשרוני הוא זוג של סדרת הספרות (פונקציה מהטבעיים אל קבוצת הספרות 0-9) ומספר טבעי שהוא מיקום של הספרה העשרונית.
- נרצה להתאים לכל ייצוג עשרוני מספר ממשי, נגדיר אותו להיות החסם העליון של כל תתי הפיתוחים העשרוניים הסופיים של המספר.
- אם [math]\displaystyle{ a_n }[/math] היא סדרת הספרות ו[math]\displaystyle{ k }[/math] הוא מיקום הנקודה העשרונית נגדיר את המספר להיות:
- [math]\displaystyle{ \sup \{10^k \sum_{i=1}^n \frac{a_i}{10^i}|n\in\mathbb{N} \} }[/math]
- דוגמא פשוטה:
- עבור הסדרה הקבועה [math]\displaystyle{ a_n =9 }[/math], ומיקום הנקודה העשרונית [math]\displaystyle{ k=0 }[/math] נקבל את הייצוג העשרוני [math]\displaystyle{ 0.999... }[/math]
- לפי ההגדרה לעיל יוצא כי:
- [math]\displaystyle{ 0.999...=\sup \{0,0.9,0.99,0.999,...\} }[/math]
- קל להוכיח כי החסם העליון של קבוצה זו הוא 1.
- 1 הוא חסם מלעיל של הקבוצה
- לכל מספר קטן מ1 יש איבר בקבוצה שגדול ממנו, כי סדרת איברי הקבוצה שואפת ל1.
- מסקנה: [math]\displaystyle{ 1=0.999... }[/math]