מערכי תרגול

• תוכן עניינים למערכי התרגול - רואי

• תרגול 1 הפרדת משתנים ומד"ר לינאריות מסדר ראשון

• תרגול 2 דוגמאות מד"ר מסדר ראשון. משוואות ברנולי, ריקטי וקלרו

• תרגול 3 מד"ר מסדר שני. מד"ר מסדר n - ורונסקיאן והורדת סדר

• תרגול 3.5 מד"ר הומוגניות, מדויקות וגורם אינטגרציה

• תרגול 4 וריאציית המקדמים ופונקציית גרין

• תרגול 5 משוואה מאפיינת למד"ר מסדר n עם מקדמים קבועים(הניחוש של אוילר). אופרטורים דיפרנציאליים ושיטת המשמיד
• שיטת המשמיד/Annihilator Method סיכום ודוגמאות (אנגלית)

• תרגול שיטת המקדמים הלא מוגדרים

• תרגול 6 המשך אדלמ"ק ושיטת המשמיד

• תרגול 7 מערכת מד"ר לינארית הומוגנית. נוסחת ליוביל. קירובי פיקארד. העברת מד"ר מסדר n למערכת של n מד"ר מסדר ראשון

• תרגול 8 מערכת מד"ר לינארית אי-הומוגנית. מערכת מד"ר עם מקדמים קבועים.

• תרגול 9 פתרון מד"ר עם מקדמים אנליטיים באמצעות טורי חזקות. משוואות איירי והרמיט. קשר בין משוואת אוילר למשוואה עם מקדמים קבועים.

• תרגול 10 נקודות סינגולריות ופתרון מד"ר בשיטת פרוביניוס.

• תרגול 11 סיכום פתרון מד"ר בעזרת טורי חזקות. משוואת בסל המותאמת (modified) ופתרונותיה.

• תרגול 12 יחסי רקורסיה וייצוג אינטגרלי לפונקציית בסל המותאמת $I_n(x)$ . התמרת לפלס ופונקציית הביסייד.

• תרגול 13 פתרון מד"ר בעזרת התמרת לפלס(שימוש בפונקציית הביסייד במד"ר מוגדרות למקוטעין) .

טבלת התמרות לפלס - שימו לב שהם מסמנים את פונקציית הביסייד ב$u(t)$ ולא $\mathcal{H}(t)$

מבוססים בעיקר על התרגולים של מר מיכאל טויטו

הערות על התרגולים

תרגול 1 : לגבי שיטת הפרדת המשתנים ששאלתם בתרגול , ודאי ניתן הסבר מדויק בהרצאה ,ובכל זאת למי שקורא את מערך התרגול ומוצא את עצמו מבולבל כאילו כפלנו ב dx .

התחלנו ממשוואה מהצורה $y'=f(x)g(y)$

אותה יש לחלק ב $g(y)$ ולעשות אינטגרל לפי x ,אז נקבל $\int \frac{y'dx}{g(y)} =\int f(x)dx$

כעת בהצבה $z=y(x)$ נקבל $\int \frac{dz}{g(z)} =\int f(x)dx+c$ ומכאן ניתן להמשיך .

בפרקטיקה אין בעיה ,ואפילו מומלץ, שתפתרו את התרגילים באותה הדרך שראינו בתרגול .

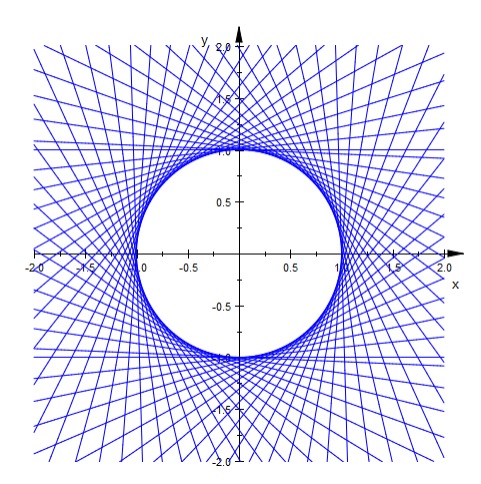
תרגול 2 : משוואת קלרו,אותה למדנו בסוף התרגול, הנה מקרה פרטי של משוואת לגרנז' $y=f(y')+xg(y')$ ,אותה לא למדנו, כאשר $g(y')=y'$ .

בנוסף, הנה תמונה יפה (באדיבות עידן אריה) למעטפת שקיבלנו עבור ישרים שמרחקם מהראשית הנו 1 ושעל ידי כך הגענו למשוואת קלרו עם $f(y')=\pm\sqrt{1+(y')^2}$

תרגול 3 : שימו לב לסכומים בצירוף הלינארי שאמורים להתחיל מ-1 ולא מ-0 . תיקנתי בקובץ .

טעות נוספת שתוקנה במהלך התרגול הנה בדוגמא שנתנו לכך שאם הורונסקיאן של n פונקציות מתאפס זה לא בהכרח גורר ש-n הפונקציות תלויות לינארית . בדוגמא לקחתי שתי פונקציות $x$ ו $\left | x \right |$ והבעיה היא ש $\left | x \right |$ אינה גזירה ב-0 . לכן לקחנו את הפונקציות $x^3$ ו $\left | x^3 \right |$

תרגול 6 : הערה חשובה לגבי התרגיל האחרון שפתרנו - בסעיפים א' ו-ב' היו נתונים חשובים ש $0<\omega$ וגם $0<\omega_0$ בלעדי נתונים אלה הפתרונות היו שונים והיה צורך לחלק למקרים. אם למשל $0>\omega_0$ אז השורשים היו ממשיים ולא מרוכבים! שכן $-\omega_0>0$ ולכן $\sqrt{-\omega_0}\in\mathbb{R}$

תרגול 9 : הבהרה לגבי פתרונות למשוואת הרמיט: עבור $a_0=1$ ו $a_1=0$ ולהפך עבור $a_0=0$ ו $a_1=1$ מקבלים פתרונות שהם או טור חזקות עם חזקות מסדר זוגי או טור חזקות עם חזקות מסדר אי-זוגי. לכן במקרה שהפתרון הוא טור חזקות מסדר זוגי כלל הנסיגה יאפס את כל החזקות מהסדר הזוגי מ-p והלאה ולכן מתקבל פתרון שהוא פולינום מסדר זוגי ובאותה הדרך מקבלים פתרונות שהם פולינומים מסדר אי-זוגי.

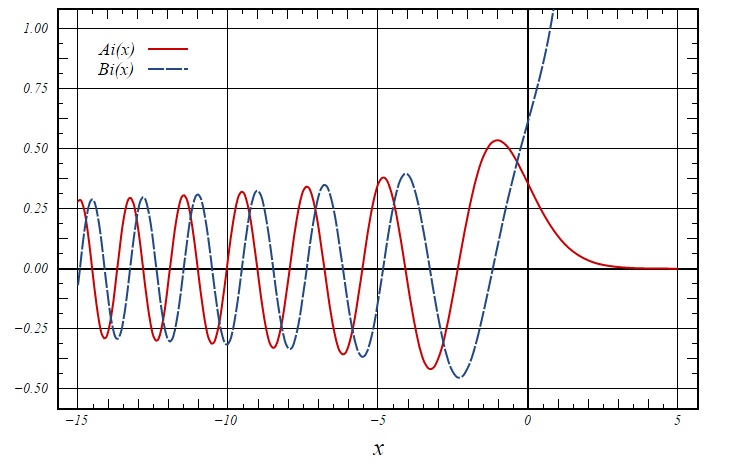
והנה תמונה מויקיפדיה לפונקציות Airy ו Bairy, דוגמא לפונקציות שעוברות בנקודה קריטית מהתנהגות של אוסילציות להתנהגות מעריכית.

תרגול 10 :לגבי המקרה הפשוט בשיטת פרוביניוס ראינו שיצאו פתרונות בת"ל וגם די ברור מאיפה מגיעה אי התלות שכן טורי החזקות שונים לחלוטין. לגבי המקרה המסובך עוד נרחיב אולם כבר ניתן לשים לב שאם ההפרש בין הפתרונות למשוואה האינדיציאלית שלם וננסה לכתוב שני פתרונות בצורת טורים אז אחד הטורים, בעל החזקה הנמוכה, יכיל את הטור השני ולכן יש לנו רק פתרון אחד, או שניים שהם ת"ל!