הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - הרצאה/1.3.11"
מתוך Math-Wiki
< משתמש:אור שחף | 133 - הרצאה
מ |
מ |
||
| שורה 10: | שורה 10: | ||
===הוכחה=== | ===הוכחה=== | ||
| − | # כיוון ש-f אינטגרבילית ב-<math>[a,b]</math> משפט 9 נותן שלכל <math>x\in[a,b]</math> f אינטגרבילית בקטע <math>[a,x_0]</math> ולכן <math>A(x)=\int\limits_a^x f</math> מוגדרת היטב. נוכיח ש-A רציפה ע"י זה שהיא מקיימת את תנאי ליפשיץ. ובכן f אינטגרבילית ובפרט היא חסומה: <math>|f(x)|\le M</math> לכל <math>x\in[a,b]</math>. כעת אם <math>x,y\in[a,b]</math> אז <math>|A(y)-A(x)|=\left|\int\limits_a^y f-\int\limits_a^x f\right|=\left|\int\limits_x^y f\right|\le M|y-x|</math> ונובע ש-A רציפה. כעת נניח ש-f רציפה בנקודה <math>x_0\in[a,b]</math>. ר"ל A גזירה שם. ובכן <math>A(x_0+\Delta x)-A(x_0)=\int\limits_a^{x_0+\Delta x} f-\int\limits_a^{x_0} f=\int\limits_{x_0}^{x_0+\Delta x} f</math> ולכן <math>\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}=\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}f</math>. נעיר ש-<math>\int\limits_{x_0}^{x_0+\Delta x} f(x_0)=f(x_0)\Delta x</math> (כי <math>f(x_0)</math> פונקציה קבועה). לכן <math>f(x_0)=\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}f(x_0)</math>. מכאן ש-<math>\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}-f(x_0)=\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}\Big(f(t)-f(x_0)\Big)\mathrm dt</math>. נותר להוכיח שכאשר <math>\Delta x\to0</math> אגף ימין (ולכן אגף שמאל) שואף ל-0. לצורך זה יהי <math>\varepsilon>0</math> נתון. כיוון ש-f רציפה ב-<math>x_0</math> קיים <math>\delta>0</math> כך שאם <math>|t-x_0|<\delta</math> אז <math>|f(t)-f(x_0)|<\varepsilon</math>. כעת נניח ש-<math>|\Delta x|<\delta</math>. אם כן האינטגרל באגף ימין הוא על קטע בין <math>x_0</math> ל-<math>x_0+\Delta x</math> ולכן כל t בקטע זה מקיים <math>|t-x_0|<\Delta x</math>. נובע שלכל t בקטע <math>|f(t)-f(x_0)|<\varepsilon</math>. יוצא שאם <math>|\Delta x|\le\delta</math> אז <math>\left|\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}-f(x_0)\right|=\left|\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}(f(t)-f(x_0))\mathrm dt\right|<\ | + | # כיוון ש-f אינטגרבילית ב-<math>[a,b]</math> משפט 9 נותן שלכל <math>x\in[a,b]</math> f אינטגרבילית בקטע <math>[a,x_0]</math> ולכן <math>A(x)=\int\limits_a^x f</math> מוגדרת היטב. נוכיח ש-A רציפה ע"י זה שהיא מקיימת את תנאי ליפשיץ. ובכן f אינטגרבילית ובפרט היא חסומה: <math>|f(x)|\le M</math> לכל <math>x\in[a,b]</math>. כעת אם <math>x,y\in[a,b]</math> אז <math>|A(y)-A(x)|=\left|\int\limits_a^y f-\int\limits_a^x f\right|=\left|\int\limits_x^y f\right|\le M|y-x|</math> ונובע ש-A רציפה. כעת נניח ש-f רציפה בנקודה <math>x_0\in[a,b]</math>. ר"ל A גזירה שם. ובכן <math>A(x_0+\Delta x)-A(x_0)=\int\limits_a^{x_0+\Delta x} f-\int\limits_a^{x_0} f=\int\limits_{x_0}^{x_0+\Delta x} f</math> ולכן <math>\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}=\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}f</math>. נעיר ש-<math>\int\limits_{x_0}^{x_0+\Delta x} f(x_0)=f(x_0)\Delta x</math> (כי <math>f(x_0)</math> פונקציה קבועה). לכן <math>f(x_0)=\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}f(x_0)</math>. מכאן ש-<math>\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}-f(x_0)=\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}\Big(f(t)-f(x_0)\Big)\mathrm dt</math>. נותר להוכיח שכאשר <math>\Delta x\to0</math> אגף ימין (ולכן אגף שמאל) שואף ל-0. לצורך זה יהי <math>\varepsilon>0</math> נתון. כיוון ש-f רציפה ב-<math>x_0</math> קיים <math>\delta>0</math> כך שאם <math>|t-x_0|<\delta</math> אז <math>|f(t)-f(x_0)|<\varepsilon</math>. כעת נניח ש-<math>|\Delta x|<\delta</math>. אם כן האינטגרל באגף ימין הוא על קטע בין <math>x_0</math> ל-<math>x_0+\Delta x</math> ולכן כל t בקטע זה מקיים <math>|t-x_0|<\Delta x</math>. נובע שלכל t בקטע <math>|f(t)-f(x_0)|<\varepsilon</math>. יוצא שאם <math>|\Delta x|\le\delta</math> אז <math>\left|\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}-f(x_0)\right|=\left|\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}(f(t)-f(x_0))\mathrm dt\right|<\frac{|\Delta x|\varepsilon}{|\Delta x|}</math>. הדבר נכון לכל <math>\varepsilon>0</math>, לכן <math>\lim_{\Delta x\to0}\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}-f(x_0)=0</math> ז"א <math>A'(x_0)</math> קיים ושווה ל-<math>f(x_0)</math>. {{משל}} |
# נתון ש-f רציפה בכל <math>[a,b]</math>. לפי החלק הקודם <math>\forall x\in[a,b]:\ A'(x)=f(x)</math>, כלומר A קדומה ל-f ב-<math>[a,b]</math>. קיים קבוע c כך ש-<math>F(x)=A(x)+c</math> לכל <math>x\in[a,b]</math>. מכאן ש-<math>F(b)-F(a)=A(b)+c-\Big(A(a)+c\Big)=A(b)-A(a)=\int\limits_a^b f-\int\limits_a^a f=\int\limits_a^b f</math>. {{משל}} | # נתון ש-f רציפה בכל <math>[a,b]</math>. לפי החלק הקודם <math>\forall x\in[a,b]:\ A'(x)=f(x)</math>, כלומר A קדומה ל-f ב-<math>[a,b]</math>. קיים קבוע c כך ש-<math>F(x)=A(x)+c</math> לכל <math>x\in[a,b]</math>. מכאן ש-<math>F(b)-F(a)=A(b)+c-\Big(A(a)+c\Big)=A(b)-A(a)=\int\limits_a^b f-\int\limits_a^a f=\int\limits_a^b f</math>. {{משל}} | ||
| שורה 16: | שורה 16: | ||
אם f רציפה בקטע <math>[a,b]</math> אז קיימת לה פונקצייה קדומה ב-<math>[a,b]</math>. | אם f רציפה בקטע <math>[a,b]</math> אז קיימת לה פונקצייה קדומה ב-<math>[a,b]</math>. | ||
====הוכחה==== | ====הוכחה==== | ||
| − | כיוון ש-f רציפה בקטע <math>[a,b]</math> כולו | + | כיוון ש-f רציפה בקטע <math>[a,b]</math> כולו <math>A(x)=\int\limits_a^x f</math> קדומה ל-f ב-<math>[a,b]</math>. |
====דוגמאות==== | ====דוגמאות==== | ||
* <math>f(x)=e^{x^2}</math>. זו פונקציה אלמנטרית ומוגדרת בכל <math>\mathbb R</math>, ולכן רציפה שם. לפי המסקנה יש לה פונקציה קדומה. זו דוגמה קלאסית לפונקציה אלמנטרית שהפונקציה הקדומה שלה לא אלמנטרית. | * <math>f(x)=e^{x^2}</math>. זו פונקציה אלמנטרית ומוגדרת בכל <math>\mathbb R</math>, ולכן רציפה שם. לפי המסקנה יש לה פונקציה קדומה. זו דוגמה קלאסית לפונקציה אלמנטרית שהפונקציה הקדומה שלה לא אלמנטרית. | ||
| שורה 31: | שורה 31: | ||
| − | + | '''הגדרה:''' עבור <math>f(x)\ge0</math> רציפה ב-<math>[a,b]</math> נגדיר את השטח שמתחת לגרף של f ע"י <math>\int\limits_a^b f</math>. לפי זה, אם <math>f(x)\le0</math> ב-<math>[a,b]</math> אז <math>\int\limits_a^b f</math> = מספר שלילי או 0 שהוא "מינוס השטח שמעל הגרף". אם f מחליפה סימן אז <math>\int\limits_a^b f</math> = השטח מעל ציר ה-x פחות השטח מתחת לציר ה-x ולכן <math>\int\limits_a^b |f|</math> = השטח בין הגרף לציר ה-x. | |
| − | + | ||
| − | '''הגדרה:''' עבור <math>f(x)\ge0</math> רציפה ב-<math>[a,b]</math> נגדיר את השטח שמתחת לגרף של f ע"י <math>\int\limits_a^b f</math>. לפי זה, אם <math>f(x)\le0</math> ב-<math>[a,b]</math> אז <math>\int\limits_a^b f</math> = מספר שלילי או 0 שהוא "מינוס השטח שמעל הגרף" | + | |
===דוגמת חישוב=== | ===דוגמת חישוב=== | ||
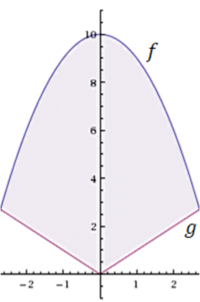
| − | + | [[קובץ:שטח בין גרפים.png|200px|ימין]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | בגרף שמשמאל ברור שהשטח בין הגרפים הוא <math>\int\limits_a^b f-g</math>, ובנימוק פשוט זה נכון בכל מקרה ש-<math>f(x)\ge g(x)</math> ב-<math>[a,b]</math>. | |
| − | |||
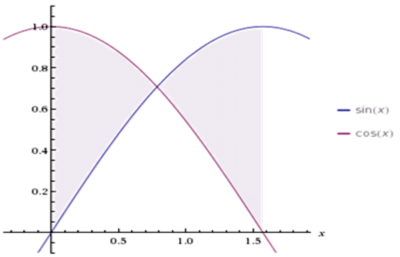
| + | למשל, נחשב את השטח שבין הגרפים <math>y=\sin(x)</math> ו-<math>y=\cos(x)</math> בקטע <math>\left[0,\tfrac\pi2\right]</math>: | ||
| + | <div align="center">[[קובץ:שטח בין סינוס לקוסינוס.png|400px]]</div> | ||
בקטע <math>\left[0,\tfrac\pi4\right]</math> מתקיים <math>\cos(x)\ge\sin(x)</math> ובקטע <math>\left[\tfrac\pi4,\tfrac\pi2\right]</math> מתקיים <math>\cos(x)\le\sin(x)</math>. לכן השטח הוא {{left|<math>\begin{align}\int\limits_0^\frac\pi2 |\cos(x)-\sin(x)|\mathrm dx&=\int\limits_0^\frac\pi4 \Big(\cos(x)-\sin(x)\Big)\mathrm dx+\int\limits_\frac\pi4^\frac\pi2 \Big(\sin(x)-\cos(x)\Big)\mathrm dx\\&=\left([\sin(x)+\cos(x)]_{x=0}^\frac\pi4\right)+\left([-\sin(x)-\cos(x)]_{x=\frac\pi4}^\frac\pi2\right)\\&=\left(\frac\sqrt22+\frac\sqrt22-(0+1)\right)+\left(-1-0+\frac\sqrt22+\frac\sqrt22\right)\\&=2\sqrt2-2\end{align}</math>}} | בקטע <math>\left[0,\tfrac\pi4\right]</math> מתקיים <math>\cos(x)\ge\sin(x)</math> ובקטע <math>\left[\tfrac\pi4,\tfrac\pi2\right]</math> מתקיים <math>\cos(x)\le\sin(x)</math>. לכן השטח הוא {{left|<math>\begin{align}\int\limits_0^\frac\pi2 |\cos(x)-\sin(x)|\mathrm dx&=\int\limits_0^\frac\pi4 \Big(\cos(x)-\sin(x)\Big)\mathrm dx+\int\limits_\frac\pi4^\frac\pi2 \Big(\sin(x)-\cos(x)\Big)\mathrm dx\\&=\left([\sin(x)+\cos(x)]_{x=0}^\frac\pi4\right)+\left([-\sin(x)-\cos(x)]_{x=\frac\pi4}^\frac\pi2\right)\\&=\left(\frac\sqrt22+\frac\sqrt22-(0+1)\right)+\left(-1-0+\frac\sqrt22+\frac\sqrt22\right)\\&=2\sqrt2-2\end{align}</math>}} | ||
{{משל}} | {{משל}} | ||
גרסה מ־12:13, 11 ביולי 2011
את ההוכחה למשפט 11 לא סיימנו בהרצאה הקודמת ולכן השלמנו אותו ב-1.3.11. חלק זה מופיע בסיכום ההרצאה הקודמת ולא בדף הנוכחי.
תוכן עניינים
האינטגרל לפי רימן (המשך)
משפט 12 (המשפט היסודי של חשבון אינטגרלי)
תהי f מוגדרת ואינטגרבילית בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
- לכל
![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) נגדיר
נגדיר 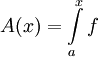 . אזי A מוגדרת היטב ורציפה ב-
. אזי A מוגדרת היטב ורציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ולכל
ולכל ![x_0\in[a,b]](/images/math/0/2/5/0256d46865eafa8df913009bb4f1d987.png) שבה f רציפה A גזירה כך ש-
שבה f רציפה A גזירה כך ש-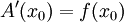 .
. - נוסחת ניוטון-לייבניץ: נניח ש-f רציפה בכל הקטע
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . אם F קדומה ל-f אז
. אם F קדומה ל-f אז ![\int\limits_a^b f=[F(x)]_{x=a}^b=F(b)-F(a)](/images/math/9/9/1/9910c3fea84d530a4ddc29cee79f0db3.png) .
.
הוכחה
- כיוון ש-f אינטגרבילית ב-
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) משפט 9 נותן שלכל
משפט 9 נותן שלכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) f אינטגרבילית בקטע
f אינטגרבילית בקטע ![[a,x_0]](/images/math/8/a/e/8aefd24e7c796fd419c690453435a4e6.png) ולכן
ולכן 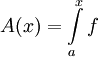 מוגדרת היטב. נוכיח ש-A רציפה ע"י זה שהיא מקיימת את תנאי ליפשיץ. ובכן f אינטגרבילית ובפרט היא חסומה:
מוגדרת היטב. נוכיח ש-A רציפה ע"י זה שהיא מקיימת את תנאי ליפשיץ. ובכן f אינטגרבילית ובפרט היא חסומה: 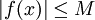 לכל
לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) . כעת אם
. כעת אם ![x,y\in[a,b]](/images/math/c/b/7/cb79e328f847e7458950b6147a06dbba.png) אז
אז 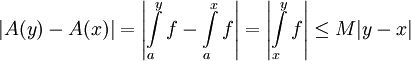 ונובע ש-A רציפה. כעת נניח ש-f רציפה בנקודה
ונובע ש-A רציפה. כעת נניח ש-f רציפה בנקודה ![x_0\in[a,b]](/images/math/0/2/5/0256d46865eafa8df913009bb4f1d987.png) . ר"ל A גזירה שם. ובכן
. ר"ל A גזירה שם. ובכן 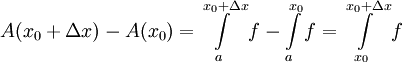 ולכן
ולכן 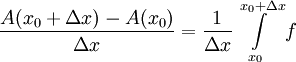 . נעיר ש-
. נעיר ש-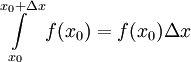 (כי
(כי 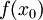 פונקציה קבועה). לכן
פונקציה קבועה). לכן 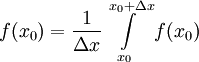 . מכאן ש-
. מכאן ש-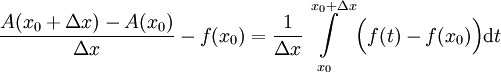 . נותר להוכיח שכאשר
. נותר להוכיח שכאשר 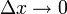 אגף ימין (ולכן אגף שמאל) שואף ל-0. לצורך זה יהי
אגף ימין (ולכן אגף שמאל) שואף ל-0. לצורך זה יהי 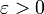 נתון. כיוון ש-f רציפה ב-
נתון. כיוון ש-f רציפה ב-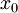 קיים
קיים 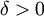 כך שאם
כך שאם 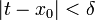 אז
אז 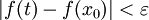 . כעת נניח ש-
. כעת נניח ש-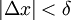 . אם כן האינטגרל באגף ימין הוא על קטע בין
. אם כן האינטגרל באגף ימין הוא על קטע בין 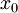 ל-
ל-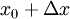 ולכן כל t בקטע זה מקיים
ולכן כל t בקטע זה מקיים 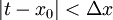 . נובע שלכל t בקטע
. נובע שלכל t בקטע 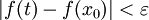 . יוצא שאם
. יוצא שאם 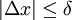 אז
אז 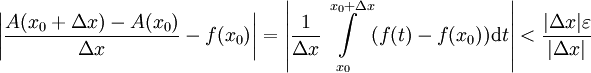 . הדבר נכון לכל
. הדבר נכון לכל 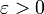 , לכן
, לכן 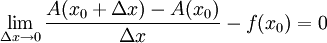 ז"א
ז"א 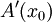 קיים ושווה ל-
קיים ושווה ל-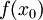 .
. 
- נתון ש-f רציפה בכל
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . לפי החלק הקודם
. לפי החלק הקודם ![\forall x\in[a,b]:\ A'(x)=f(x)](/images/math/b/3/e/b3eff8bb43fdeda0d0edfb6294af6278.png) , כלומר A קדומה ל-f ב-
, כלומר A קדומה ל-f ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . קיים קבוע c כך ש-
. קיים קבוע c כך ש-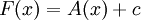 לכל
לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) . מכאן ש-
. מכאן ש-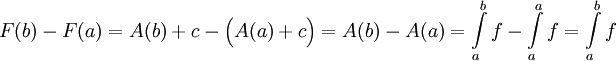 .
. 
מסקנה
אם f רציפה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אז קיימת לה פונקצייה קדומה ב-
אז קיימת לה פונקצייה קדומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
הוכחה
כיוון ש-f רציפה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כולו
כולו 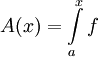 קדומה ל-f ב-
קדומה ל-f ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
דוגמאות
-
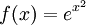 . זו פונקציה אלמנטרית ומוגדרת בכל
. זו פונקציה אלמנטרית ומוגדרת בכל 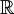 , ולכן רציפה שם. לפי המסקנה יש לה פונקציה קדומה. זו דוגמה קלאסית לפונקציה אלמנטרית שהפונקציה הקדומה שלה לא אלמנטרית.
, ולכן רציפה שם. לפי המסקנה יש לה פונקציה קדומה. זו דוגמה קלאסית לפונקציה אלמנטרית שהפונקציה הקדומה שלה לא אלמנטרית. -
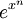 כאשר
כאשר 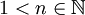
-
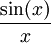
-
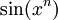
-
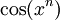
תרגילים לחידוד
- נגדיר
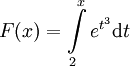 . נמצא את
. נמצא את 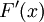 : לפי חלק א של משפט 12 מתקיים
: לפי חלק א של משפט 12 מתקיים 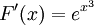 .
. 
- נגדיר
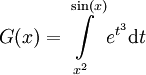 . נמצא את
. נמצא את 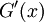 : נגדיר
: נגדיר 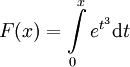 ולכן
ולכן 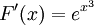 . לפי זה
. לפי זה 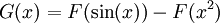 ולפיכך, ע"פ כלל השרשרת,
ולפיכך, ע"פ כלל השרשרת, 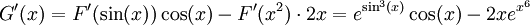 .
. 
הגדרה: עבור 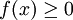 רציפה ב-
רציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) נגדיר את השטח שמתחת לגרף של f ע"י
נגדיר את השטח שמתחת לגרף של f ע"י 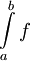 . לפי זה, אם
. לפי זה, אם 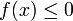 ב-
ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אז
אז 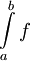 = מספר שלילי או 0 שהוא "מינוס השטח שמעל הגרף". אם f מחליפה סימן אז
= מספר שלילי או 0 שהוא "מינוס השטח שמעל הגרף". אם f מחליפה סימן אז 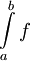 = השטח מעל ציר ה-x פחות השטח מתחת לציר ה-x ולכן
= השטח מעל ציר ה-x פחות השטח מתחת לציר ה-x ולכן 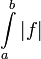 = השטח בין הגרף לציר ה-x.
= השטח בין הגרף לציר ה-x.
דוגמת חישוב
בגרף שמשמאל ברור שהשטח בין הגרפים הוא 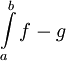 , ובנימוק פשוט זה נכון בכל מקרה ש-
, ובנימוק פשוט זה נכון בכל מקרה ש-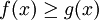 ב-
ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
למשל, נחשב את השטח שבין הגרפים 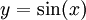 ו-
ו-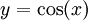 בקטע
בקטע ![\left[0,\tfrac\pi2\right]](/images/math/4/e/7/4e77a1302dd5d47f289db594d8f17338.png) :
:
![\left[0,\tfrac\pi4\right]](/images/math/a/d/4/ad443a23a524ee9b06986eb6c71924c7.png) מתקיים
מתקיים 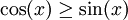 ובקטע
ובקטע ![\left[\tfrac\pi4,\tfrac\pi2\right]](/images/math/5/5/7/5570c0484decdccf0a3970f8cb0633d3.png) מתקיים
מתקיים 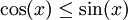 . לכן השטח הוא
. לכן השטח הוא ![\begin{align}\int\limits_0^\frac\pi2 |\cos(x)-\sin(x)|\mathrm dx&=\int\limits_0^\frac\pi4 \Big(\cos(x)-\sin(x)\Big)\mathrm dx+\int\limits_\frac\pi4^\frac\pi2 \Big(\sin(x)-\cos(x)\Big)\mathrm dx\\&=\left([\sin(x)+\cos(x)]_{x=0}^\frac\pi4\right)+\left([-\sin(x)-\cos(x)]_{x=\frac\pi4}^\frac\pi2\right)\\&=\left(\frac\sqrt22+\frac\sqrt22-(0+1)\right)+\left(-1-0+\frac\sqrt22+\frac\sqrt22\right)\\&=2\sqrt2-2\end{align}](/images/math/0/5/d/05d97e9286e66c19908e1846480de557.png)