פתרון אינפי 1, תשס"ב, מועד א,
(המבחן )
חלק א'
1) התשובה היא ב'. שלא כמו בלמה של קנטור, חסרה ההנחה של שאיפת גודל ההפרש ל-  .
.
 היא סדרה עולה החסומה מלעיל ע"י
היא סדרה עולה החסומה מלעיל ע"י 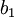 (באינדוקציה -
(באינדוקציה - 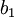 גדולה יותר מכל שאר איברי
גדולה יותר מכל שאר איברי 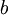 שגדולים יותר מכל איברי
שגדולים יותר מכל איברי  ) ולכן מתכנסת. בצורה דומה,
) ולכן מתכנסת. בצורה דומה,  היא סדרה יורדת החסומה מלרע ע"י
היא סדרה יורדת החסומה מלרע ע"י 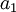 ולכן מתכנסת. פוסל את ג', ד'. נותר להראות באמצעות דוגמא את ב':
ולכן מתכנסת. פוסל את ג', ד'. נותר להראות באמצעות דוגמא את ב':
דוגמא: 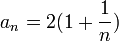 ,
, 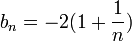 .
.
2) התשובה היא ב'.
הפרכה לג', ד': 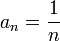 . ברור
. ברור 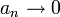 אבל
אבל ![\lim\limits_{n\to\infty}{\sqrt[n]{a_n}}=1](/images/math/9/8/5/985cc17c11e66b29fb921790df4f6ed4.png) .
אותה סדרה היא גם הפרכה טריוויאלית לסעיף א'. ב' נכון שכן
.
אותה סדרה היא גם הפרכה טריוויאלית לסעיף א'. ב' נכון שכן 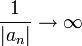 .
.
(נובע ישירות מההגדרות, שכן אם 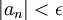 אז
אז 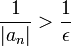 .)
פורמלית: יהי
.)
פורמלית: יהי 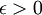 . מתקיים
. מתקיים 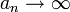 ולכן לכל
ולכן לכל  קיים
קיים 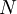 כך ש-
כך ש- 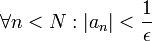 , כלומר כך ש-
, כלומר כך ש- 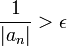 . מש"ל.
. מש"ל.
3) ד'. 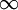 או
או  נק'. שתי דוגמאות:
נק'. שתי דוגמאות:
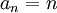 ,
, 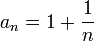 . באחת יש אינסוף נקודות
(סדרה מתכנסת ולכן חסומה, ולכן כל מה שגדול מהחסם העליון שלה), בשניה נניח בשלילה שיש נקודה
. באחת יש אינסוף נקודות
(סדרה מתכנסת ולכן חסומה, ולכן כל מה שגדול מהחסם העליון שלה), בשניה נניח בשלילה שיש נקודה 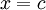 בחיתוך ונתבונן במקום
בחיתוך ונתבונן במקום 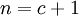 , כלומר בקטע
, כלומר בקטע 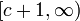 שלא מכיל את
שלא מכיל את 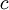 כלל, בסתירה.
כלל, בסתירה.
4) התשובה היא ד'. הפרכה לא', ב', ג': נגדיר
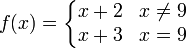 ,
, 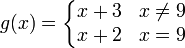
אז ברור שההרכבה רציפה, שכן
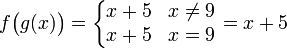 והוכחנו רציפות כל הפונקציות הלינאריות.
והוכחנו רציפות כל הפונקציות הלינאריות.
גם  וגם
וגם  אינן רציפות ב-
אינן רציפות ב- 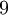 , ולכן זאת הפרכה ל-ג' והוכחה ל-ד'.
, ולכן זאת הפרכה ל-ג' והוכחה ל-ד'.
5) עבור 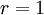 מקבלים טור מתכנס לפי לייבניץ, מה שפוסל את ג',ד'. עבור
מקבלים טור מתכנס לפי לייבניץ, מה שפוסל את ג',ד'. עבור 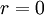 הטור מתכנס (ל-
הטור מתכנס (ל-  ) מה שפוסל את ב'. עבור
) מה שפוסל את ב'. עבור 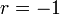 מקבלים
מקבלים 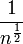 , שמתבדר לפי העיבוי כי
, שמתבדר לפי העיבוי כי 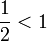 . פוסל את א', לכן נותרנו רק עם ה', שהיא התשובה הנכונה. (ישירות, נראה שהטור מתכנס בהחלט עבור
. פוסל את א', לכן נותרנו רק עם ה', שהיא התשובה הנכונה. (ישירות, נראה שהטור מתכנס בהחלט עבור 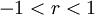 , ובפרט מתכנס, ואז נבדוק את המקרים הנותרים.)
, ובפרט מתכנס, ואז נבדוק את המקרים הנותרים.)
6 הורוביץ) ברור שב'. הפרכה לא',ג':
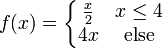
עולה ממש ואינה רציפה בקטע 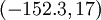 .
.
הוכחת ב': בשלילה, 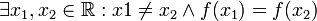 .
.
בסתירה לכך ש-  עולה ממש, שהרי בה"כ
עולה ממש, שהרי בה"כ 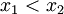 ולכן
ולכן 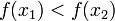 בסתירה להיותם שווים.
בסתירה להיותם שווים.
6 זלצמן וקליין) ג'. ד"ר שיין הוכיח טענה כמעט זהה - 7.8.
הוכחה:  עולה ממש ולכן לפי ההשאלה הקודמת היא חח"ע.
עולה ממש ולכן לפי ההשאלה הקודמת היא חח"ע.  גזירה ב
גזירה ב ובפרט רציפה בסביבתה. לכן הפונ' ההפוכה מוגדרת ורציפה בסביבת
ובפרט רציפה בסביבתה. לכן הפונ' ההפוכה מוגדרת ורציפה בסביבת 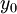 . כעת, לפי ההנחה
. כעת, לפי ההנחה  גזירה ב-
גזירה ב-  ולכן
ולכן 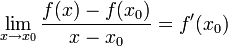 .
.
מכאן נקבל 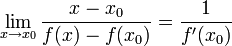 , בהנחה שהנגזרת שונה מ-
, בהנחה שהנגזרת שונה מ-  . לכן
. לכן 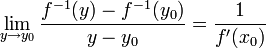 ובפרט קיים. לכן הפונ' ההפוכה גזירה בנקודה
ובפרט קיים. לכן הפונ' ההפוכה גזירה בנקודה  . בכיוון ההפוך, נראה את ה- contrapositive: אם הפונ' ההפוכה גזירה אז הנגזרת שווה להופכי של הנגזרת של
. בכיוון ההפוך, נראה את ה- contrapositive: אם הפונ' ההפוכה גזירה אז הנגזרת שווה להופכי של הנגזרת של  , ולכן הנגזרת שונה מ-
, ולכן הנגזרת שונה מ-  (זה לא נימוק לגמרי פורמלי).
(זה לא נימוק לגמרי פורמלי).
חלק ב'
7) 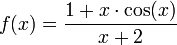 .
.
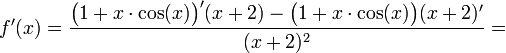
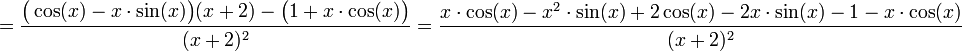
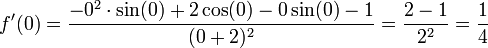
זהו שיפוע המשיק.
כעת, נציב במש' ישר עם הנקודה 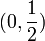 , ונקבל:
, ונקבל:
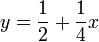 .
.
8) היה במערכי התרגול [[1]] עבור סכום עד 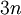 . הפתרון כמעט זהה. נראה שהיא מונוטונית וחסומה:
. הפתרון כמעט זהה. נראה שהיא מונוטונית וחסומה:
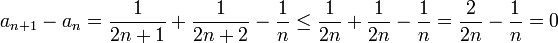 ולכן הסדרה היא מונוטונית יורדת. באינדוקציה הסדרה חסומה מלרע ע"י
ולכן הסדרה היא מונוטונית יורדת. באינדוקציה הסדרה חסומה מלרע ע"י  (כי סכום חיוביים הוא חיובי). לכן הסדרה מתכנסת.
(כי סכום חיוביים הוא חיובי). לכן הסדרה מתכנסת.
9) הטור מתבדר, שכן התנאי הההכרחי אינו מתקיים; הסדרה אינה שואפת ל-
(המשפט הקודם נכון, אבל זוועתי להוכחה, ויש דרך קלה:)
 כאשר
כאשר  שואף לאינסוף, אלא שואפת לאינסוף.
שואף לאינסוף, אלא שואפת לאינסוף.
בשביל לבדוק התכנסות בהחלט, נשתמש במבחן קושי: נחפש את הגבול העליון של 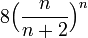 .
.
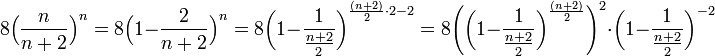
קיבלנו גורם 8, גורם 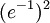 , וגורם 1. לכן הגבול, ובפרט הגבול העליון, הוא
, וגורם 1. לכן הגבול, ובפרט הגבול העליון, הוא 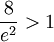 , (מסכן מי ששכח להביא מחשבון - זה יוצא די קרוב ל-1) ולכן הטור הנתון אינו מתכנס בהחלט. יתרה מכך, עפ"י המשפט שהוכחנו (משפט קושי המעודן, לתלמידי ד"ר שיין) נובע מכך שהטור המקורי מתבדר.
, (מסכן מי ששכח להביא מחשבון - זה יוצא די קרוב ל-1) ולכן הטור הנתון אינו מתכנס בהחלט. יתרה מכך, עפ"י המשפט שהוכחנו (משפט קושי המעודן, לתלמידי ד"ר שיין) נובע מכך שהטור המקורי מתבדר.
חלק ג'
10) הפרכה: ניקח 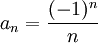 ,
, 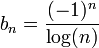 .
לפי לייבניץ הטור
.
לפי לייבניץ הטור 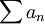 מתכנס, וברור ש-
מתכנס, וברור ש-  שואפת ל-
שואפת ל-  שכן
שכן 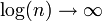 , אבל המכפלה
, אבל המכפלה 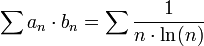 מתבדרת לפי מבחן העיבוי, שיעורי הבית, הבוחן ומבחן האינטגרל:)
מתבדרת לפי מבחן העיבוי, שיעורי הבית, הבוחן ומבחן האינטגרל:)
(נגדיר 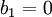 בשביל ענייני תחום-הגדרה, ברור שזה לא משנה)
בשביל ענייני תחום-הגדרה, ברור שזה לא משנה)
11) נגדיר פונקצייה 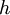 על-ידי
על-ידי ![\forall x\in [-1,1]: h(x)=f(x)-x^2](/images/math/6/6/8/66818bd6b12aacb1eebeaae7d6e13bad.png) . כעת, נתבונן ב-
. כעת, נתבונן ב- 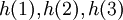 :
:
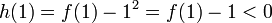 ואילו
ואילו 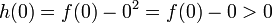 , ולכן לפי משפט ערך הביניים ל-
, ולכן לפי משפט ערך הביניים ל- 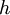 יש שורש (כלומר היא מתאפסת) בנקודה כלשהי בקטע
יש שורש (כלומר היא מתאפסת) בנקודה כלשהי בקטע 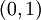 .
.
באותו האופן, 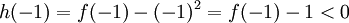 ולכן יש ל-
ולכן יש ל- 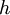 שורש בקטע
שורש בקטע 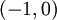 . כל שורש של
. כל שורש של 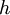 הוא נקודה בה הפונ' שוות, ומצאנו שיש לפחות 2 כאלה.
הוא נקודה בה הפונ' שוות, ומצאנו שיש לפחות 2 כאלה.
12 זלצמן) הוכחה:
מכיון ש- 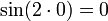 אז ניתן להגדיר את
אז ניתן להגדיר את  "מחדש" כפונקציה מפוצלת באופן הבא (מבלי לשנות בעצם את הגדרת
"מחדש" כפונקציה מפוצלת באופן הבא (מבלי לשנות בעצם את הגדרת  ).
). 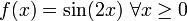 .
.
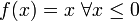 .
.
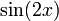 רציפה ובעלת מחזור
רציפה ובעלת מחזור 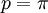 ולכן רציפה במ"ש ב-
ולכן רציפה במ"ש ב- 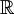 ולכן רציפה במ"ש גם בכל קטע חלקי ל-
ולכן רציפה במ"ש גם בכל קטע חלקי ל- 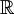 , ובפרט בקרן החיובית הסגורה
, ובפרט בקרן החיובית הסגורה 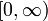 .
.
ידוע ש-  רציפה במ"ש ב-
רציפה במ"ש ב- 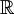 ולכן רציפה במ"ש גם בכל קטע חלקי ל-
ולכן רציפה במ"ש גם בכל קטע חלקי ל- 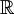 , ובפרט בקרן השלילית הסגורה
, ובפרט בקרן השלילית הסגורה ![(-\infty,0]](/images/math/f/9/d/f9d75a40b8eadac31117745d2255ef61.png) .
.
לכן  רציפה במ"ש ב-
רציפה במ"ש ב- 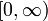 וכמו כן ב-
וכמו כן ב- ![(-\infty,0]](/images/math/f/9/d/f9d75a40b8eadac31117745d2255ef61.png) . לקרנות הנ"ל יש נקודה משותפת (
. לקרנות הנ"ל יש נקודה משותפת ( ) ולכן (לפי משפט ממערכי התרגול)
) ולכן (לפי משפט ממערכי התרגול)  רציפה באיחוד הקרנות, שהוא הישר הממשי כולו.
רציפה באיחוד הקרנות, שהוא הישר הממשי כולו.
12 קליין) נגדיר פונקציה 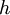 על-ידי
על-ידי 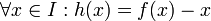 .
.
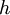 מתאפסת בשתי נקודות שונות בקטע
מתאפסת בשתי נקודות שונות בקטע 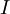 ולכן לפי משפט רול קיימת נקודה בפנים הקטע בה נגזרתה מתאפסת. כלומר
ולכן לפי משפט רול קיימת נקודה בפנים הקטע בה נגזרתה מתאפסת. כלומר 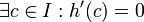 . לכן
. לכן 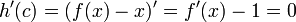 , ומכאן ש-
, ומכאן ש- 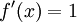 . מש"ל.
. מש"ל.
12 הורוביץ) פונ' רציפה בקטע סגור מקבלת בו מקסימום ומינימום (ויירשטראס II). בשלילה, נניח שהאינפימום אינו חיובי, ומייד נקבל סתירה שכן הפונ' צריכה לקבל את האינפימום שלה, ובנקודה זאת הפונ' תהיה אי-חיובית, בסתירה. 