פתרונות לקורס לינארית 2 לתיכוניסטים תש"ע - תרגיל 4
תוכן עניינים
תרגיל 4
- שימו לב - זה לא פתרון רשמי של ארז, אלא הפתרון שלי לתרגיל. --Ohad Abarbanel 11:48, 8 בדצמבר 2009 (UTC)
שאלה 1
הטענה לא נכונה. דוגמה נגדית:
![A=\left[ \begin{matrix}
2 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 2 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 2 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 2 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 2 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 2 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 2 \\
\end{matrix} \right],B=\left[ \begin{matrix}
2 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 2 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 2 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 2 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 2 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 2 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 2 \\
\end{matrix} \right]](/images/math/5/3/7/537cc14dddb83a5aade50771016eecda.png)
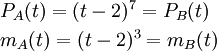
הריבוי הגיאומטרי של 2 בשתי המטריצות הוא 3. המטריצות לא דומות כיוון שצורת הז'ורדן שלהן (הן עצמן) שונות.
שאלה 2
סעיף א'
![\begin{align}
& 1)\left[ \begin{matrix}
2 & 0 & 0 & 0 & 0 \\
0 & 2 & 0 & 0 & 0 \\
0 & 0 & 2 & 0 & 0 \\
0 & 0 & 0 & 5 & 0 \\
0 & 0 & 0 & 0 & 5 \\
\end{matrix} \right]\quad 2)\left[ \begin{matrix}
2 & 1 & 0 & 0 & 0 \\
0 & 2 & 0 & 0 & 0 \\
0 & 0 & 2 & 0 & 0 \\
0 & 0 & 0 & 5 & 0 \\
0 & 0 & 0 & 0 & 5 \\
\end{matrix} \right]\quad 3)\left[ \begin{matrix}
2 & 1 & 0 & 0 & 0 \\
0 & 2 & 1 & 0 & 0 \\
0 & 0 & 2 & 0 & 0 \\
0 & 0 & 0 & 5 & 0 \\
0 & 0 & 0 & 0 & 5 \\
\end{matrix} \right] \\
& 4)\left[ \begin{matrix}
2 & 1 & 0 & 0 & 0 \\
0 & 2 & 1 & 0 & 0 \\
0 & 0 & 2 & 0 & 0 \\
0 & 0 & 0 & 5 & 1 \\
0 & 0 & 0 & 0 & 5 \\
\end{matrix} \right]\quad 5)\left[ \begin{matrix}
2 & 0 & 0 & 0 & 0 \\
0 & 2 & 0 & 0 & 0 \\
0 & 0 & 2 & 0 & 0 \\
0 & 0 & 0 & 5 & 1 \\
0 & 0 & 0 & 0 & 5 \\
\end{matrix} \right]\quad 6)\left[ \begin{matrix}
2 & 1 & 0 & 0 & 0 \\
0 & 2 & 0 & 0 & 0 \\
0 & 0 & 2 & 0 & 0 \\
0 & 0 & 0 & 5 & 1 \\
0 & 0 & 0 & 0 & 5 \\
\end{matrix} \right] \\
\end{align}](/images/math/9/e/c/9ec778a9fd773f07e37b6ced61253b2d.png)
סעיף ב'
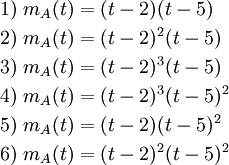
סעיף ג'
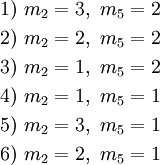
שאלה 3
סעיף א'
A משולשית, לכן אברי האלכסון הם הע"ע של A כולל הריבוי האלגברי, לכן
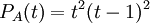 .
.
נמצא את הפולינום המינימלי:
נבדוק את
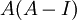 :
:
![\left[ \begin{matrix}
1 & 2 & 3 & 4 \\
0 & 0 & 2 & 3 \\
0 & 0 & 1 & 2 \\
0 & 0 & 0 & 0 \\
\end{matrix} \right]\left[ \begin{matrix}
0 & 2 & 3 & 4 \\
0 & -1 & 2 & 3 \\
0 & 0 & 0 & 2 \\
0 & 0 & 0 & -1 \\
\end{matrix} \right]=\left[ \begin{matrix}
0 & 0 & 7 & 12 \\
0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
\end{matrix} \right]\ne 0](/images/math/d/7/f/d7fd7cf083ac0dda55ff3139a88ee2da.png)
נבדוק את
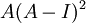 :
:
![\left[ \begin{matrix}
0 & 0 & 7 & 12 \\
0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
\end{matrix} \right]\left[ \begin{matrix}
0 & 2 & 3 & 4 \\
0 & -1 & 2 & 3 \\
0 & 0 & 0 & 2 \\
0 & 0 & 0 & -1 \\
\end{matrix} \right]=\left[ \begin{matrix}
0 & 0 & 0 & 2 \\
0 & 0 & 0 & -1 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
\end{matrix} \right]\ne 0](/images/math/4/0/8/4085bd473ebd017cc83aa5d443399ed2.png)
האפשרות היחידה שנותרה היא
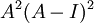 לכן הפולינום המינימלי הוא
לכן הפולינום המינימלי הוא
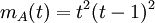 , לכן מטריצת הז'ורדן של A היא:
, לכן מטריצת הז'ורדן של A היא:
![\left[ \begin{matrix}
1 & 1 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 \\
\end{matrix} \right]](/images/math/4/f/6/4f6f5fba3dbe062672c62a043004021c.png)
סעיף ב'
![I-A=\left[ \begin{matrix}
0 & -2 & -3 & -4 \\
0 & 1 & -2 & -3 \\
0 & 0 & 0 & -2 \\
0 & 0 & 0 & 1 \\
\end{matrix} \right]](/images/math/9/7/f/97f1bef400e61f7851c7f34dfbbfc5f3.png)
נניח שהפולינום המינימלי של I-A הוא ממעלה הקטנה מ-4, כלומר קיים
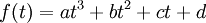 כך ש
כך ש
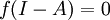 , כלומר:
, כלומר:
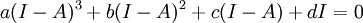
אם נפתח סוגריים נקבל פולינום ממעלה הקטנה מ-4 המאפס את A, וזוהי סתירה למינימליות של הפולינום המינימלי שמצאנו ב-א', לכן הפולינום המינימלי של I-A הוא ממעלה 4, והאפשרות היחידה היא
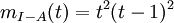 , לכן מטריצת הז'ורדן של I-A היא:
, לכן מטריצת הז'ורדן של I-A היא:
![\left[ \begin{matrix}
1 & 1 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 \\
\end{matrix} \right]](/images/math/4/f/6/4f6f5fba3dbe062672c62a043004021c.png)
צורות הז'ורדן של A ושל I-A שוות לכן
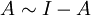 .
.
שאלה 4
נמצא את
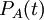 :
:
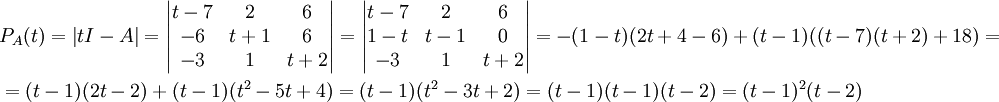
נמצא את
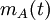 :
:
נבדוק את
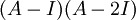 :
:
![(A-I)(A-2I)=\left[ \begin{matrix}
6 & -2 & -6 \\
6 & -2 & -6 \\
3 & -1 & -3 \\
\end{matrix} \right]\left[ \begin{matrix}
5 & -2 & -6 \\
6 & -3 & -6 \\
3 & -1 & -4 \\
\end{matrix} \right]=\left[ \begin{matrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} \right]](/images/math/5/5/a/55a2a053b47e4f832a2a5e85fb295903.png)
לכן הפולינום המינימלי הוא
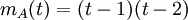 .
.
נבדוק האם
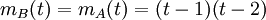 :
:
![(B-I)(B-2I)=\left[ \begin{matrix}
-3 & -3 & 2 \\
-1 & 1 & 0 \\
-6 & -3 & 3 \\
\end{matrix} \right]\left[ \begin{matrix}
-4 & -3 & 2 \\
-1 & 0 & 0 \\
-6 & -3 & 2 \\
\end{matrix} \right]=\left[ \begin{matrix}
3 & 3 & -2 \\
3 & 3 & -2 \\
9 & 9 & -6 \\
\end{matrix} \right]\ne 0](/images/math/a/9/1/a9182c04ddb459cc2cc398c33f06d9dc.png)
מצאנו ש
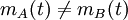 לכן בהכרח A לא דומה ל-B.
לכן בהכרח A לא דומה ל-B.
שאלה 5
חלק ראשון - שאלה 1
סעיף א'
לפי המשפט היסודי של האלגברה לכל פולינום ממעלה n יש n שורשים מרוכבים, לכן
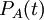 מתפרק לגורמים לינאריים מעל
מתפרק לגורמים לינאריים מעל
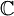 .
לפי משפט השילוש קיימת מטריצה B משולשת כך ש
.
לפי משפט השילוש קיימת מטריצה B משולשת כך ש
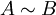 , כלומר קיימת מטריצה P הפיכה כך ש
, כלומר קיימת מטריצה P הפיכה כך ש
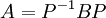 , לכן מתקיים:
, לכן מתקיים:
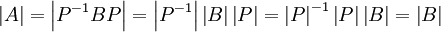
על אלכסון המטריצה B נמצאים הערכים העצמיים של A, ו-B משולשית לכן
 שווה למכפלת אברי האלכסון שהיא מכפלת הערכים העצמיים של A.
שווה למכפלת אברי האלכסון שהיא מכפלת הערכים העצמיים של A.
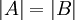 לכן
לכן
 היא מכפלת הערכים העצמיים של A.
היא מכפלת הערכים העצמיים של A.
סעיף ב'
נניח בשלילה שקיימת
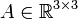 כך ש
כך ש
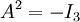 .
.
ל-A יש 3 ערכים עצמיים (לא בהכרח שונים). נסמנם
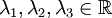 .
.
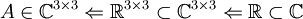 לכן לפי א'
לכן לפי א'
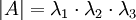 .
.
לפי ההנחה,
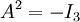 , לכן:
, לכן:
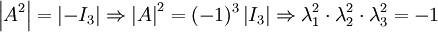
מכיוון ש
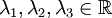 ,
מתקיים
,
מתקיים
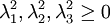 לכן גם
לכן גם
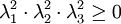 וזו סתירה לכך ש
וזו סתירה לכך ש
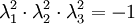 ,
לכן לא קיימת
,
לכן לא קיימת
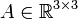 כך ש
כך ש
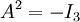 .
.
חלק שני - שאלה 5
סעיף א'
ריבוי אלגברי של ע"ע
 הוא המספר הגדול ביותר
הוא המספר הגדול ביותר
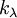 כך ש
כך ש
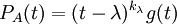 .
.
או במילים פשוטות: הריבוי האלגברי של  הוא החזקה של
הוא החזקה של 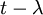 בפולינום האופייני.
בפולינום האופייני.
ריבוי גיאומטרי של ע"ע  הוא
הוא
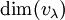 כאשר
כאשר
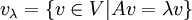 .
.
או במילים פשוטות: הריבוי הגיאומטרי של הוא מימד המרחב העצמי של
הוא מימד המרחב העצמי של 
סעיף ב'
נמצא את
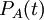 :
:
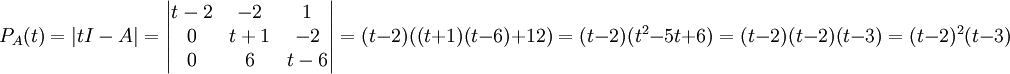
נמצא את הפולינום המינימלי:
נבדוק את
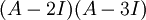 :
:
![(A-2I)(A-3I)=\left[ \begin{matrix}
0 & 2 & -1 \\
0 & -3 & 2 \\
0 & -6 & 4 \\
\end{matrix} \right]\left[ \begin{matrix}
- & 2 & -1 \\
0 & -4 & 2 \\
0 & -6 & 3 \\
\end{matrix} \right]=\left[ \begin{matrix}
0 & -2 & 1 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{matrix} \right]\ne 0](/images/math/f/d/a/fda1fd6a1a27accba46f24c4819baf88.png)
האפשרות היחידה שנותרה לפולינום המינימלי היא
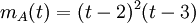 .
.
לפי משפט בלוק הז'ורדן הגדול ביותר של 2 במטריצת הז'ורדן של A הוא בגודל 2 ובלוק הז'ורדן הגדול ביותר של 3 הוא 1, לכן מטריצת הז'ורדן של A היא:
![\left[ \begin{matrix}
2 & 1 & 0 \\
0 & 2 & 0 \\
0 & 0 & 3 \\
\end{matrix} \right]](/images/math/0/4/1/041468b9c8b745a8a1d4ee42487e0174.png)