שיחה:88-132 סמסטר א' תשעא/ ארכיון 3
תוכן עניינים
עזרה דחופה בגבולות
שלום לכולם,
הנושא של גבולות, הוא פשוט נושא כל כך קשה, שרק את ההגדרה לקח לי בערך 3 שעות להבין. כל הוכחה או תרגיל שהיו קשורים לגבולות לא הבנתי בכלל, ואני חייב עזרה. אפשר אלגוריתם מלא לפתרון בעיה שבא צריך למצוא ולהוכיח גבול של סדרה או להוכיח שאין גבול של סדרה?
למשל בתרגיל 3, בשאלה 1 א. צריך למצוא גבול לסדרה 1 חלקי שורש n. הבנתי שהגבול הזה הוא 0. צריך למצוא N אפסילון שבשבילו לכל n גדול מN אפסילון יתקיים ש 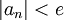 . חיפשתי ערכים מתאימים ובעזרת מחשבון מצאתי שלכל
. חיפשתי ערכים מתאימים ובעזרת מחשבון מצאתי שלכל ![N=[1/(e^2)]](/images/math/3/6/d/36d379d02269da87c8ec8019b17ef085.png) כשב[] אני מתכוון לתקרה.
אבל איך עכשיו אני מתקדם? איך לעבור מ nים שגדולים מN, לan? תודה!
כשב[] אני מתכוון לתקרה.
אבל איך עכשיו אני מתקדם? איך לעבור מ nים שגדולים מN, לan? תודה!
תשובה
הפתרון הוא דומה לדברים שעשינו בכיתה. צריך להתקיים 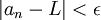 כלומר במקרה הזה
כלומר במקרה הזה 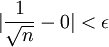 ולכן אחרי פיתוח קל מקבלים שצריך להתקיים
ולכן אחרי פיתוח קל מקבלים שצריך להתקיים 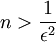 . לכל n אי השיוויון האחרון מתקיים אם"ם אי השיוויון המקורי מתקיים.
. לכל n אי השיוויון האחרון מתקיים אם"ם אי השיוויון המקורי מתקיים.
כל מה שנותר הוא לבחור הוא 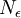 כלשהו כך ש
כלשהו כך ש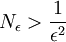 ואז ברור שלכל
ואז ברור שלכל 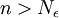 מתקיים
מתקיים 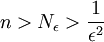 ולכן מתקיים אי השיוויון הרצוי
ולכן מתקיים אי השיוויון הרצוי 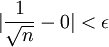 . --ארז שיינר 15:46, 29 באוקטובר 2010 (IST)
. --ארז שיינר 15:46, 29 באוקטובר 2010 (IST)
- אפשר גם דוגמה להוכחה שסדרה היא מתבדרת?
- הדוגמא הקלאסית הינה
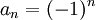 . נניח בשלילה שהסדרה מתכנסת לגבול L חיובי (ההוכחה עבור שליליים דומה). לכן לכל אפסילון (ובפרט עבור
. נניח בשלילה שהסדרה מתכנסת לגבול L חיובי (ההוכחה עבור שליליים דומה). לכן לכל אפסילון (ובפרט עבור 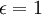 ) יש מקום בסדרה (
) יש מקום בסדרה (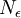 ) כך שהחל ממנו והלאה כל איברי הסדרה (לכל
) כך שהחל ממנו והלאה כל איברי הסדרה (לכל 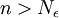 ) מקיימים
) מקיימים 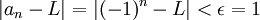 . לכן בפרט, יש איברים אי זוגיים שמקיימים את זה, ניקח אחד כזה ונקבל
. לכן בפרט, יש איברים אי זוגיים שמקיימים את זה, ניקח אחד כזה ונקבל 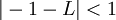 אבל
אבל 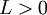 ולכן
ולכן 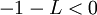 ולכן
ולכן 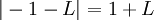 וביחד מקבלים
וביחד מקבלים 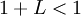 ולכן
ולכן 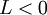 וזו סתירה. לכן לא יכול להיות גבול L חיובי כזה, וכמו שאמרתי ההוכחה עבור השלילים ואפס דומה. --ארז שיינר 17:37, 29 באוקטובר 2010 (IST)
וזו סתירה. לכן לא יכול להיות גבול L חיובי כזה, וכמו שאמרתי ההוכחה עבור השלילים ואפס דומה. --ארז שיינר 17:37, 29 באוקטובר 2010 (IST)
- תודה רבה!!
- הדוגמא הקלאסית הינה
- (שואל אחר) בקשר להוכחה של 1א, אני השתמשתי באריתמטיקה של גבולות (באופן דומה למה שמצויין בשאלה הזו). זה בסדר? (ד"א, מצטרף לשאלה השנייה שם - האם צ"ל ש-
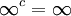 אם c>0, או שזה מספיק טריוויאלי?). אור שחףשיחה 22:23, 30 באוקטובר 2010 (IST)
אם c>0, או שזה מספיק טריוויאלי?). אור שחףשיחה 22:23, 30 באוקטובר 2010 (IST)
שאלה 1ב.
בקשר לסינוס של n!, מתכוונים שמה שבתוך הסינוס הוא במעלות או ברדיאנים? כי יוצאות תוצאות שונות.
- זה לא משנה, אתה צריך להגיע לזה ש
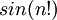 בכלל לא משפיע על הגבול. רמז לזה הוא ש
בכלל לא משפיע על הגבול. רמז לזה הוא ש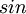 היא פונקציה חסומה בין 1 ל-1-. גיל טנקוס :)
היא פונקציה חסומה בין 1 ל-1-. גיל טנקוס :)
- למה זה לא משנה? הצבתי ערכים הולכים וגדלים במחשבון. כשהצבתי במעלות, יצא לי שמn=6 ומעלה, הסינוס מתאפס והסדרה היא קבועה על 0. אך כשהצבתי ברדיאנים הסדרה לא התאפסה ויצאו ערכים שונים לגמרי, כך שזה כן משפיע! ולא הבנתי מה זה אומר שהפונקציה חסומה, אתה יכול להסביר? תודה!
- סינוס באוניברסיטה הוא תמיד ברדיאנים, זה קודם כל.
שנית סינוס לא מתאפס בערכים גבוהים לא ברדאינים ולא במעלות (איך זה הגיוני בכלל שהוא יתאפס בסולם אחד אבל לא בסולם אחר).פונקציה חסומה בין 1 למינוס 1, כלומר שהערכים שלה קטנים שווים ל1 וגדולים שווים למינוס אחד. למשל, הפונקציה לא יכולה לקבל את הערכים 50 או מינוס 100 (לעולם). --ארז שיינר 17:41, 29 באוקטובר 2010 (IST)- אני עושה במחשבון
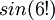 וכשהמחשבון במצב של מעלות זה נותן לי 0 (וכך גם בכל הערכים מעל 6). איך זה?
וכשהמחשבון במצב של מעלות זה נותן לי 0 (וכך גם בכל הערכים מעל 6). איך זה? - והנה, הפונקציה קיבלה ערך מחוץ ל1 ול1-! אתה לא מתכוון שהפונקציה -מוציאה- (לא "מקבלת") ערכים ביו 1 ל1-?
- ודבר אחרון, אני יודע מה זה אומר חסומה, התכוונתי, האם אפשר הסבר לגבי איך זה מתקשר לתרגיל? תודה!
- אפס הוא כן 'בין' אחד למינוס אחד. על מנת להבין את הקשר, מומלץ לקרוא את התרגול שם דברנו על משפט שקשור לסדרות חסומות. ולגבי המעלות, אתה צודק זו טעות שלי, וזה כן הגיוני שזה קבוע אפס (כי זה הופך להיות כפולה שלימה של 360 מעלות, ולא משנה במה תכפיל זה ישאר כפולה שלימה של 360 מעלות). בכל אופן, מדובר על רדיאנים. --ארז שיינר 18:06, 29 באוקטובר 2010 (IST)
- 0 זה בין 1 ל-1 אבל הפונקציה מקבל 6! ולא 0.
- ועכשיו הבנתי למה התכוונת. כאשר אומרים מקבלת, הכוונה היא שזה הערך המתקבל. כך או כך סינוס n! חסום לכל n.
- חיפשתי ולא מצאתי. אפשר עזרה לגבי העניין של החסימה? האם יש משפט שאומר שאם פונקציה היא חסומה מלמעלה או מלמטה, אז הכפל שלה עם פונקציה אחרת "לא משפיע" על הגבול של הפונקציה המתקבלת? כי זה לא נראה לי כל כך נכון, כי אם ניקח למשל את הפונקציה הקבועה an=0, היא חסומה, וכן הפונקציה הקבועה bn=1, אזי מכפלת הפונקציות צריכה להיות 1 (כי לכאורה ה0 לא משפיע על 1) כשבעצם הגבול של הפונקציה an=0*1 הוא 0.
- בתרגיל כיתה נניח אתה לא מוצא, מה לגבי תרגיל הבית? יש שם שאלה על סדרה חסומה? --ארז שיינר 18:29, 29 באוקטובר 2010 (IST)
- נחמד! תודה רבה! כשאומרים סדרה קטנה מסדרה אחרת (an<bn) מתכוונים שכל איברי הסדרה קטנים מאיברי הסדרה השנייה?
- הכוונה היא שהם קטנים איבר איבר, לא שכל איברי סדרה אחת קטנה מכל איברי הסדרה השנייה. נגיד איברי הסדרה
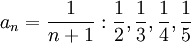 קטנים מאיברי הסדרה
קטנים מאיברי הסדרה 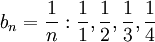 --ארז שיינר 18:58, 29 באוקטובר 2010 (IST)
--ארז שיינר 18:58, 29 באוקטובר 2010 (IST)
- הכוונה היא שהם קטנים איבר איבר, לא שכל איברי סדרה אחת קטנה מכל איברי הסדרה השנייה. נגיד איברי הסדרה
- נחמד! תודה רבה! כשאומרים סדרה קטנה מסדרה אחרת (an<bn) מתכוונים שכל איברי הסדרה קטנים מאיברי הסדרה השנייה?
- בתרגיל כיתה נניח אתה לא מוצא, מה לגבי תרגיל הבית? יש שם שאלה על סדרה חסומה? --ארז שיינר 18:29, 29 באוקטובר 2010 (IST)
- חיפשתי ולא מצאתי. אפשר עזרה לגבי העניין של החסימה? האם יש משפט שאומר שאם פונקציה היא חסומה מלמעלה או מלמטה, אז הכפל שלה עם פונקציה אחרת "לא משפיע" על הגבול של הפונקציה המתקבלת? כי זה לא נראה לי כל כך נכון, כי אם ניקח למשל את הפונקציה הקבועה an=0, היא חסומה, וכן הפונקציה הקבועה bn=1, אזי מכפלת הפונקציות צריכה להיות 1 (כי לכאורה ה0 לא משפיע על 1) כשבעצם הגבול של הפונקציה an=0*1 הוא 0.
- אפס הוא כן 'בין' אחד למינוס אחד. על מנת להבין את הקשר, מומלץ לקרוא את התרגול שם דברנו על משפט שקשור לסדרות חסומות. ולגבי המעלות, אתה צודק זו טעות שלי, וזה כן הגיוני שזה קבוע אפס (כי זה הופך להיות כפולה שלימה של 360 מעלות, ולא משנה במה תכפיל זה ישאר כפולה שלימה של 360 מעלות). בכל אופן, מדובר על רדיאנים. --ארז שיינר 18:06, 29 באוקטובר 2010 (IST)
- אני עושה במחשבון
- סינוס באוניברסיטה הוא תמיד ברדיאנים, זה קודם כל.
- למה זה לא משנה? הצבתי ערכים הולכים וגדלים במחשבון. כשהצבתי במעלות, יצא לי שמn=6 ומעלה, הסינוס מתאפס והסדרה היא קבועה על 0. אך כשהצבתי ברדיאנים הסדרה לא התאפסה ויצאו ערכים שונים לגמרי, כך שזה כן משפיע! ולא הבנתי מה זה אומר שהפונקציה חסומה, אתה יכול להסביר? תודה!
תרגיל 3, שאלה 5ב
צריך להוכיח או להפריך שאם 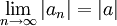 אז
אז 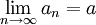 . כמובן שזה לא נכון אם a<0, ולכן אני שואל אם התכוונתם ל-
. כמובן שזה לא נכון אם a<0, ולכן אני שואל אם התכוונתם ל-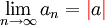 (וכנ"ל לגבי 5ג). תודה, 89.139.184.191 17:39, 29 באוקטובר 2010 (IST)
(וכנ"ל לגבי 5ג). תודה, 89.139.184.191 17:39, 29 באוקטובר 2010 (IST)
- אין טעות בשאלה (ומגניב האדום הזה) --ארז שיינר 17:42, 29 באוקטובר 2010 (IST)
תרגיל 3 שאלה 5 ד
לא הבנתי עד הסוף למה הכוונה מיתכנס במובן הרחב.. כי ברור שאם הסידרה שואפת לאפס אז ההופכי שלה ישאף לאינסוף האם עיקרון זה מספיק בישביל להגיד שהסידרה מיתכנסת במובן הרחב?
תשובה
למי זה ברור? אין דברים ברורים, יש הוכחות. וכאשר מושג לא מובן חייבים לחפש את ההגדרה המדוייקת שלו. במקרה הזה, סדרה מתכנסת במובן הרחב לאינסוף אם לכל 0<M קיים מקום בסדרה 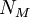 כך שהחל ממנו והלאה (לכל
כך שהחל ממנו והלאה (לכל 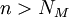 ) מתקיים
) מתקיים 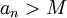 .
.
סדרה מתכנסת במובן הרחב למינוס אינסוף אם לכל 0<M קיים מקום בסדרה 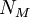 כך שהחל ממנו והלאה (לכל
כך שהחל ממנו והלאה (לכל 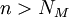 ) מתקיים
) מתקיים 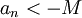 .
.
עכשיו סתם נקודת למחשבה - תחשוב על הסדרה 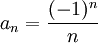 .
.
שאלה 7
הגעתי למצב שנישאר לי רק להוכיח את שורש N של N מתכנסת לאחד היסתכלתי על התרגיל שפתרתה בכיתה ואני לא מבין את ההוכחה לזה..האם זה קשור לאי שיוויון ברנולי כי לא לימדתה את זה
תשובה
אל מי אתה מדבר? כי אני (ארז) הוכחתי את אי שיוויון ברנולי, ואני מניח שגם המרצה. שנית צריך להוכיח בתרגיל ש![\sqrt[n]{a}\rightarrow 1](/images/math/f/f/f/fffefb41e10787cb70097e71c54144fa.png) עבור a קבוע. ידוע לנו מהכיתה ש
עבור a קבוע. ידוע לנו מהכיתה ש![\sqrt[n]{n}\rightarrow 1](/images/math/9/1/2/91269b276969d0d2b414be55cb0ab84e.png) . מעבר לכך אתה מוזמן להגיד מה לא הבנת מההוכחה בכיתה. --ארז שיינר 13:19, 30 באוקטובר 2010 (IST)
. מעבר לכך אתה מוזמן להגיד מה לא הבנת מההוכחה בכיתה. --ארז שיינר 13:19, 30 באוקטובר 2010 (IST)
אריתמטיקה של גבולות
המרצה שלנו לא הוכיח שלכל סדרה 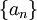 שמתכנסת במובן הרחב מתקיים:
שמתכנסת במובן הרחב מתקיים: 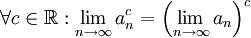 או
או 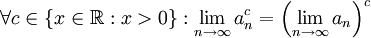 אם הגבול או an שווה 0. (הוא הוכיח רק שזה נכון עבור
אם הגבול או an שווה 0. (הוא הוכיח רק שזה נכון עבור 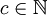 ). מותר להשתמש בזה? 82.166.216.211 19:29, 30 באוקטובר 2010 (IST)
). מותר להשתמש בזה? 82.166.216.211 19:29, 30 באוקטובר 2010 (IST)
תשובה
אתה צודק שזה לא הוכח בהרצאה, אפשר להניח שזה נכון (רק אתה מתכוונת לסדרה שמתכנסת, לא מתכנסת במובן הרחב) --ארז שיינר 19:40, 30 באוקטובר 2010 (IST)
- אני כן מתכוון במובן הרחב, כאשר
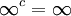 לכל
לכל 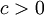 . 82.166.216.211 20:09, 30 באוקטובר 2010 (IST)
. 82.166.216.211 20:09, 30 באוקטובר 2010 (IST)
- נו, אז את זה אפשר להוכיח דיי בקלות ישירות.
- אבל צריך להוכיח (במבחנים ובש"ב)? או שזה שמותר להשתמש בזה כמשפט? תודה, 82.166.216.211 20:28, 30 באוקטובר 2010 (IST)
- בתרגיל הזה עדיף להראות, באופן כללי לרוב לא תצטרך. --ארז שיינר 22:31, 30 באוקטובר 2010 (IST)
- אבל צריך להוכיח (במבחנים ובש"ב)? או שזה שמותר להשתמש בזה כמשפט? תודה, 82.166.216.211 20:28, 30 באוקטובר 2010 (IST)
- נו, אז את זה אפשר להוכיח דיי בקלות ישירות.
עזרה בהוכחת 1 ד.
הפונקציה מתכנסת לאינסוף. כדי להוכיח שהיא לא מתכנסת לאף גבול, אני יכול או להוכיח שהיא מתכנסת במובן הרחב לאינסוף, או להוכיח פשוט שהיא לא מתכנסת לגבול ממשי, נכון? ניסיתי להוכיח שהיא לא מתכנסת לאף גבול ממשי, ע"י הנחה בשלילה, ונתקעתי, לא הצלחתי להוכיח.
אז ניסיתי להוכיח שהיא מתכנסת במובן הרחב לאינסוף, אבל שוב נתקעתי, כי הגעתי לאי שוויון 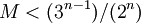 , ומכאן אני צריך להגיע למשוואה שבצד אחד שלה יש רק n, וזה בלתי אפשרי.
אפשר עזרה לגבי מה לעשות? תודה רבה!
, ומכאן אני צריך להגיע למשוואה שבצד אחד שלה יש רק n, וזה בלתי אפשרי.
אפשר עזרה לגבי מה לעשות? תודה רבה!
- תסתכל על ההערה בתחילת התרגיל, ותחשוב איך להשתמש בה כאן. --ארז שיינר 20:21, 30 באוקטובר 2010 (IST)
- אתה מתכוון לתזכורת? דבר ראשון, לא צריך להוכיח את זה? דבר שני, יש כאן מנה של פונקציות מעריכיות שזה לא בהכרח מתכנס לאינסוף!
- התזכורת כן, ואין צורך להוכיח אותה. תחשוב איך להפוך את זה לצורה של התזכורת --ארז שיינר 20:57, 30 באוקטובר 2010 (IST)
- הבנתי, יש לי רק שאלה: המשפט מהתזכורת עובד גם עבור פונקציה של n במקום n? כלומר
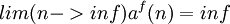 ? (מקווה שתבין את צורת הכתיבה שלי)
? (מקווה שתבין את צורת הכתיבה שלי)
- אין כרגע בקורס פונקציות, לכן זה לא רלוונטי לתרגיל, אבל כן, קבוע גדול מאחד בחזקת משהו ששואף לאינסוף בהכרח ישאף לאנסוף. --ארז שיינר 21:35, 30 באוקטובר 2010 (IST)
- אבל השאלה היא האם צריך להוכיח שכשn שואף לאינסוף אז הפונקציה של n שנמצאת במעריך של הקבוע, שואף לאינסוף. כי אם כן, אז התרגיל נשאר באותו רמת קושי ולא עשינו פה כלום בעצם (יוצא לי a בחזקת משהו עם לוגריתם).
- מה הגבול של
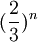 ? --ארז שיינר 22:28, 30 באוקטובר 2010 (IST)
? --ארז שיינר 22:28, 30 באוקטובר 2010 (IST)
- מה הגבול של
- אבל השאלה היא האם צריך להוכיח שכשn שואף לאינסוף אז הפונקציה של n שנמצאת במעריך של הקבוע, שואף לאינסוף. כי אם כן, אז התרגיל נשאר באותו רמת קושי ולא עשינו פה כלום בעצם (יוצא לי a בחזקת משהו עם לוגריתם).
- אין כרגע בקורס פונקציות, לכן זה לא רלוונטי לתרגיל, אבל כן, קבוע גדול מאחד בחזקת משהו ששואף לאינסוף בהכרח ישאף לאנסוף. --ארז שיינר 21:35, 30 באוקטובר 2010 (IST)
- הבנתי, יש לי רק שאלה: המשפט מהתזכורת עובד גם עבור פונקציה של n במקום n? כלומר
- התזכורת כן, ואין צורך להוכיח אותה. תחשוב איך להפוך את זה לצורה של התזכורת --ארז שיינר 20:57, 30 באוקטובר 2010 (IST)
- אתה מתכוון לתזכורת? דבר ראשון, לא צריך להוכיח את זה? דבר שני, יש כאן מנה של פונקציות מעריכיות שזה לא בהכרח מתכנס לאינסוף!
תרגול 3-שאלה 7
ארז,שבוע טוב! אמרת שבשאלה 7 צריך להוכיח בשלילה שL שונה מאפס כדי להגיע לכך שהוא שווה לאפס. אפשר עוד כיוון בבקשה כי זה לא הולך לי..? (הצלחתי להוכיח רק את הצד שאם הגבול שווה 0 אז היא מתכנסת..) תודה!
- רמז: אריתמטיקה של גבולות. מה אפשר לעשות כאשר גבול הסדרה שונה מאפס? --ארז שיינר 21:36, 30 באוקטובר 2010 (IST)
כלל לופיטל
מותר להשתמש בכלל לופיטל? ובכלל, האם מותר להשתמש בכל מה שלמדנו בביה"ס? תודה, אור שחףשיחה 22:16, 30 באוקטובר 2010 (IST)
תשובה
לא. הרי אין כרגע פונקציות בכלל, רק סדרות, וגם אם כן היה זה לא היה מותר עד שלא נלמד את כלל לופיטל. אפשר להשתמש בידע מהתיכון בחוקי חזקות, לוגריתמים, וטריגונומטריה --ארז שיינר 22:30, 30 באוקטובר 2010 (IST)
תרגיל 3, שאלה 7
יכול להיות שכבר מאוחר מדי, אבל לגבי שאלה 7 - כתוב שהסדרה bn אינה מתכנסת. הכוונה היא שאינה מתכנסת ממש או שאינה מתכנסת גם במובן הרחב? (זה משנה את דרך הפתרון שלי) תודה.
- נאמר שהיא לא מתכנסת, לכן (ולפי דעתי, וכך פתרתי), היא לא מתכנסת כלל, אחרת היו אומרים שהיא לא מתכנסת במובן הרחב או שהיא לא מתכנסת ממש (אבל ייתכן שהיא תתכנס למובן הרחב)... גל א.
- כאשר רושמים לא מתכנסת הכוונה היא לא מתכנסת במובן הצר (אלא אם רשום במפורש אחרת. אבל פה ממילא מדובר בסדרה חסומה, לכן בוודאי היא אינה מתכנסת במובן הרחב. --ארז שיינר 11:23, 31 באוקטובר 2010 (IST)
בקשה לדחייה
שיעורי הבית באינפחי קודמים את התרגול.
למדנו בתרגול האחרון איך לענות על שאלות כמו שהיו להגשה אתמול ובשיעורי הבית החדשים עוד לא למדנו בתרגול.
אשמח אם נוכל לקבל דיה ולהתאזן גם עם הקבוצה השניה.
תשובה
תפנה למתרגל שלך באופן אישי עם בקשה כזו --ארז שיינר 19:49, 1 בנובמבר 2010 (IST)
שאלה כללית על סדרות
ארז, אתה יכול בבקשה להסביר מה ההבדל בין סדרה מתכנסת לסדרה חסומה ומה זה אומר לי אם סדרה מתכנסת או אם סדרה חסומה? ואיך זה קשור לגבול של הסדרה ולגבולות החלקיים? תודה!
תשובה
סדרה מתכנסת אם היא מקיימת את הגדרת הגבול (שנמצאת בדף הראשי של הקורס באתר). זה קורה כאשר, בערך, כל איברי הסדרה מתקרבים לנקודה אחת - הגבול (זו לא אמירה מדוייקת כמובן). סדרה הינה חסומה, אם קיים M כך שהתנאי הבא מתקיים 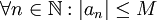 כלומר כל איברי הסדרה חסומים על ידי גדול קבוע כלשהו (זו כן אמירה מדוייקת). הם לא חייבים להתקרב לנקודה מסוימת, פשוט אסור להם להיות גדולים או קטנים מידי.
כלומר כל איברי הסדרה חסומים על ידי גדול קבוע כלשהו (זו כן אמירה מדוייקת). הם לא חייבים להתקרב לנקודה מסוימת, פשוט אסור להם להיות גדולים או קטנים מידי.
דוגמאות:
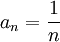 סדרה שמתכנסת לאפס
סדרה שמתכנסת לאפס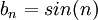 סדרה חסומה (שכן כל האיברים שלה בין מינוס אחד לבין אחד), אבל היא אינה מתכנסת (איבריה זזים כל הזמן בין מינוס אחד לאחד ואינם מתקרבים לנקודה מסוימת).
סדרה חסומה (שכן כל האיברים שלה בין מינוס אחד לבין אחד), אבל היא אינה מתכנסת (איבריה זזים כל הזמן בין מינוס אחד לאחד ואינם מתקרבים לנקודה מסוימת).
גבול של סדרה קיים אם היא מתכנסת, הוא הנקודה אליה איברי הסדרה מתקרבים כפי שתארתי למעלה. גבול חלקי של סדרה הוא נקודה שמתקרבים אליה אינסוף איברים מהסדרה, אבל לא כולם (כלומר, יש תת-סדרה שמתכנסת אליו)
לדוגמא:
- נתבונן בסדרה
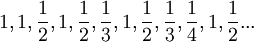
אין לה גבול, מכיוון שאין נקודה שכל איברי הסדרה מתקרבים אליה. אבל למשל  הוא גבול חלקי, כי אנחנו יכולים לקחת את תת הסדרה שמכילה אך ורק את האיברים ששוים לחצי.
הוא גבול חלקי, כי אנחנו יכולים לקחת את תת הסדרה שמכילה אך ורק את האיברים ששוים לחצי.