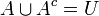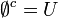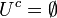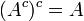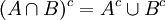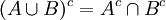תרגול 2 מדמח קיץ תשעז
תוכן עניינים
פרדיקטים וכמתים
בניגוד לאטומים שהם ללא משתנים הפרדיקטים הינם פונקציות התלויות במשתנים. לדוגמא ניתן להגדיר את הפרדיקט  להיות x הינו סטודנט באוניברסיטה.
להיות x הינו סטודנט באוניברסיטה.
כיוון שאטומים הם ללא משתנים הם יכולים להיות T או F אבל לא שניהם. לעומתם פרדיקטים הם תלויים במשתנים ולכן ערך האמת שלהם יקבע לפי ההצבה במשתנים. למשל הפרדיקט 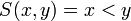 יהיה נכון במקרה ש
יהיה נכון במקרה ש 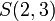 ולא נכון במקרה ש
ולא נכון במקרה ש 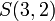 . כלומר לכל הצבה במשתני הפרדיקטים נקבל פסוק. הערה: משמשים בקשרים גם בפרדיקטים למשל
. כלומר לכל הצבה במשתני הפרדיקטים נקבל פסוק. הערה: משמשים בקשרים גם בפרדיקטים למשל 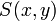 הפרדיקט המוגדר
הפרדיקט המוגדר 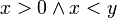
בנוסף, ניתן להוסיף כמתים.
הכמת "לכל" 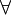 והכמת "קיים"
והכמת "קיים" 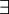
תפקיד מרכזי של הכמת הוא להבהיר את כוונת הטענה. למשל הטענה ש "סטונדט הוא יצור חרוץ" יכולה לקבל 2 משמעויות בעזרת הכמתים. או "כל סטודנט הוא יצור חרוץ" או "קיים סטודנט שהוא יצור חרוץ".
הטענה הראשונה טוענת לגבי כלל הסטודנטים (אם רוצים להוכיח כי הטענה נכונה צריך לעבור בין כל הסטודנטים ולוודא שהם חרוצים ואם רוצים להוכיח כי הטענה לא נכונה מספיק למצוא סטודנט אחד שאינו חרוץ).
לעומתה הטענה השניה טוענת שניתן למצוא סטודנט אחד (לפחות) שהוא חרוץ (אם רוצים להוכיח את הטענה צריך למצוא סטודנט שהוא חרוץ ואם רוצים להוכיח כי הטענה לא נכונה צריך לעבור בין כל הסטודנטים ולוודא שהם אינם חרוצים
הצרן: לכל מספר p גדול מ-1: (p ראשוני) אמ"מ (אם הוא מחלק מכפלת מספרים אז הוא מחלק את אחד המספרים).
פתרון:
ההצרנה 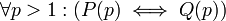 כאשר
כאשר
-
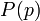 הוא הפרדיקט "p" הוא ראשוני.
הוא הפרדיקט "p" הוא ראשוני. -
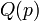 הוא הפרדיקט
הוא הפרדיקט 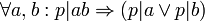
הערה: שמות המשתנים אינם חשובים למשל עבור הפרדיק 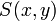 המוגדר
המוגדר 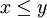 הפסוק
הפסוק 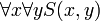 הוא זהה לפסוק
הוא זהה לפסוק
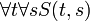
הערה: סדר הכמתים כן משתנה (לפעמים) למשל 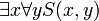 לא שקול לפסוק
לא שקול לפסוק 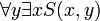 . דוגמא: הצרן את המשפט "לכל מספר טבעי יש מספר טבעי הגדול ממנו" פתרון:
. דוגמא: הצרן את המשפט "לכל מספר טבעי יש מספר טבעי הגדול ממנו" פתרון: 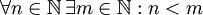 לעומת זאת
לעומת זאת 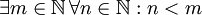 פירושו שקיים מספר טבעי שגדול מכל המספרים הטבעיים.
פירושו שקיים מספר טבעי שגדול מכל המספרים הטבעיים.
נשים לב כי בשביל לקבוע אם הפסוק 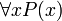 אנחנו צריכים לדעת איזה x ים "חוקיים" (בהנחה שאנחנו יודעים את P).
אנחנו צריכים לדעת איזה x ים "חוקיים" (בהנחה שאנחנו יודעים את P).
שלילת פסוקים
מהי השלילה של הפסוק "לכל סיר יש מכסה המתאים לו", או "לכל מאכל, יש מישהו שמכין אותו טעים"?
בעת שלילה של פסוק לוגי, הכמתים 'לכל' ו'קיים' מתחלפים זה עם זה, והשלילה עוברת הלאה. את השלילה על הקשרים ניתן לבצע באמצעות טאוטולוגיות וטבלאות אמת.
תרגיל
כתבו פסוק השקול לפסוק הבא ללא שימוש בקשר השלילה.
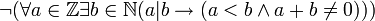
פיתרון:
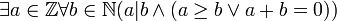
תרגיל
הוכח או הפרך (משתני הפרדיקט נלקחים מהטבעיים):
א. 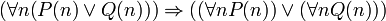
ב. 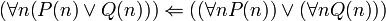
פיתרון:
א. הפרכה. ניקח את P להיות 1 על הזוגיים ו-0 על אי-זוגיים, ןQ להיפך.אכן כל מספר טבעי הוא זוגי או אי-זוגי, אך זה לא נכון שכל מספר הוא זוגי או שכל מספר הוא אי-זוגי.
ב. הוכחה: יהי  לפי הנתון מתקיים
לפי הנתון מתקיים 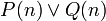 כדרוש.
כדרוש.
קבוצות
ההגדרה האינטואיטיבית לקבוצה הינה "אוסף של איברים". ההגדרה הזו מובילה לסתירות לוגיות כגון "פרדוקס ראסל". נביט בקבוצה הבאה:
- X=אוסף כל הקבוצות שאינן שייכות לעצמן
אם X שייכת לקבוצה הזו, אזי היא אינה שייכת לקבוצה. אולם, אם היא אינה שייכת לקבוצה אזי היא כן שייכת לקבוצה.
סתירה אינה מקובלת במחוזות המתמטיקאים, ולכן הגדירו את "תורת הקבוצות האקסיומטית" העוקפת בעייה זו. ניתן לקרוא יותר על נושא זה בקישור לעיל, עבורנו מספיקה ההגדרה האינטואיטיבית.
אם כן, נחזור להגדרתנו הנאיבית; קבוצה הינה אוסף של איברים שונים. בקבוצה אין משמעות לסדר האיברים, ואיבר אינו יכול להופיע פעמיים. דוגמאות ל3 קבוצות:
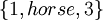 ,
, 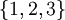 ו
ו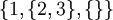
איבר השייך לקבוצה אנו מסמנים בסימן 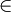 . למשל
. למשל 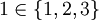 , ואילו
, ואילו 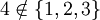 . שימו לב שגם
. שימו לב שגם 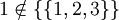 שכן האיבר היחיד בקבוצה זו הינה הקבוצה
שכן האיבר היחיד בקבוצה זו הינה הקבוצה 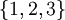 .
.
- אומרים שקבוצה A מוכלת בקבוצה B (מסומן
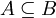 ) אם כל האיברים בA הם גם איברים בB. בשפה מדויקת, A מוכלת בB אם מתקיים
) אם כל האיברים בA הם גם איברים בB. בשפה מדויקת, A מוכלת בB אם מתקיים 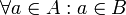 .
.
- דוגמא:
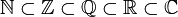 כאשר
כאשר
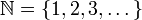 המספרים הטבעיים
המספרים הטבעיים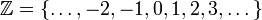 המספרים השלמים
המספרים השלמים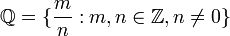 המספרים הרציונאלים (שברים)
המספרים הרציונאלים (שברים)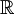 המספרים הממשיים ("כל המספרים" על הישר)
המספרים הממשיים ("כל המספרים" על הישר)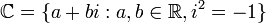 המספרים המרוכבים
המספרים המרוכבים
- חיתוך של שתי קבוצות A ו B הינו אוסף האיברים השייכים גם לA וגם לB (מסומן
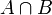 ). מתקיים ש
). מתקיים ש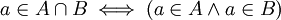 .
.
- איחוד של שתי קבוצות A ו B הינו אוסף האיברים השייכים לA או לB (מסומן
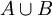 ). מתקיים ש
). מתקיים ש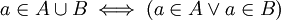 .
.
- קבוצות הן שוות אם הן מכילות את אותם האיברים. הדרך הנפוצה להוכיח שיוויון הינה הכלה דו כיוונית: A=B אם ורק אם
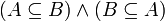 .
.
- A הפרש B הינה הקבוצה המכילה את כל האיברים בA שאינם בB (מסומן A\B). מתקיים ש
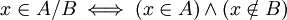 .
.
- ההפרש הסימטרי בין שתי קבוצות A וB הוא אוסף האיברים הנמצאים באחת הקבוצות אך לא בחיתוך (מסומן
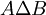 ). מתקיים ש
). מתקיים ש 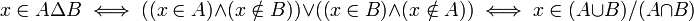
דוגמא:
יהיו 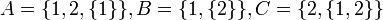 קבוצות.
קבוצות.
אזי:
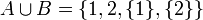
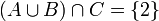
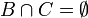
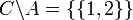
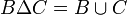
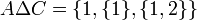
- הצרן תנאי השקול לכך שקבוצה C לא מוכלת באיחוד של A ו-B.
תכונות האיחוד והחיתוך (דומה לכפל וחיבור)
- אסוציאטיביות:
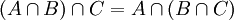 (וכנ"ל לגבי איחוד)
(וכנ"ל לגבי איחוד) - חילוף:
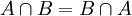 (וכנ"ל לגבי איחוד)
(וכנ"ל לגבי איחוד) - דיסטריביוטיביות:
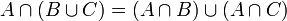 , וגם
, וגם 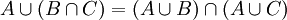
תרגיל
נוכיח שההפרש הסימטרי הוא קיבוצי, כלומר: לכל שלש קבוצות 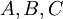 מתקיים :
מתקיים : 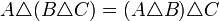
פתרון
אפשרי ע"י טבלת אמת הנקראת טבלת שכיחויות.
תרגיל
הוכח כי:
א. הקבוצה הריקה 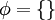 מוכלת בכל קבוצה A
מוכלת בכל קבוצה A
ב. 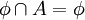
ג. 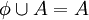
פתרון
א. יש להוכיח את הפסוק הבא: 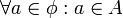 . אבל מכיוון שאין איברים בקבוצה הריקה, המשפט הזה נכון באופן ריק. זכרו ששקר גורר כל דבר, לכן האטום "איבר a שייך לקבוצה הריקה" גורר כל דבר.
. אבל מכיוון שאין איברים בקבוצה הריקה, המשפט הזה נכון באופן ריק. זכרו ששקר גורר כל דבר, לכן האטום "איבר a שייך לקבוצה הריקה" גורר כל דבר.
ב. 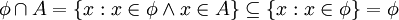 כעזרת א קיבלנו הכלה בשני הכיוונים ולכן שיוויון.
כעזרת א קיבלנו הכלה בשני הכיוונים ולכן שיוויון.
ג. 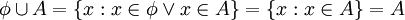 כי
כי 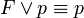 .
.
הכללה לאיחודים וחיתוכים כל שהם
מוטיבציה: הגדרנו את החיתוך והאיחוד עבור שתי קבוצות. לעיתים נרצה לחתוך או לאחד יותר קבוצות, לדוגמא נרצה לדבר על חיתוכן של 17 הקבוצות 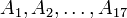 . מכיוון שחיתוך ואיחוד הן פעולות אסוציטיביות, ניתן לרשום
. מכיוון שחיתוך ואיחוד הן פעולות אסוציטיביות, ניתן לרשום 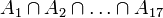 , וזה ביטוי חד משמעי. אך צורת רישום זו היא ארוכה, ולכן אנו מסמנים את החיתוך הזה בקיצור הבא:
, וזה ביטוי חד משמעי. אך צורת רישום זו היא ארוכה, ולכן אנו מסמנים את החיתוך הזה בקיצור הבא: 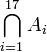 . לעיתים נרצה לחתוך או לאחד אוסף אינסופי של קבוצות, ולכך באה ההכללה הבאה:
. לעיתים נרצה לחתוך או לאחד אוסף אינסופי של קבוצות, ולכך באה ההכללה הבאה:
הגדרה:
יהיו 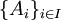 אוסף קבוצות כאשר
אוסף קבוצות כאשר 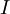 הוא קבוצת אינדקסים אזי נגדיר את האיחוד והחיתוך של אוסף הקבוצות כך:
הוא קבוצת אינדקסים אזי נגדיר את האיחוד והחיתוך של אוסף הקבוצות כך:
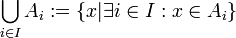
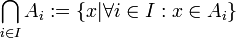 . כאן יש להניח שקבוצת האינדקסים
. כאן יש להניח שקבוצת האינדקסים 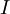 לא ריקה.
לא ריקה.
דוגמא:
נגדיר ![\forall n\in \mathbb{N} \; A_n:=[n,n+1]](/images/math/b/e/6/be669fb7637e3c1c6e6bd1431436da46.png) אזי
אזי
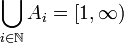
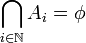
תרגיל
נתון 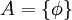 ונתון
ונתון 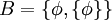 . סמן את הביטויים הנכונים:
. סמן את הביטויים הנכונים:
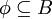 (כן)
(כן)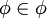 (לא)
(לא)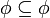 (כן)
(כן)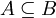 (כן)
(כן)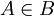 (כן)
(כן)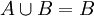 (כן)
(כן)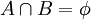 (לא)
(לא)
תרגיל
הוכח כי 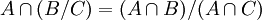
פתרון
דרך גרירות לוגיות:
![x\in A\cap (B/C)\iff (x\in A) \and [(x\in B) \and (x\notin C)]\iff [(x\in A) \and (x\in B) \and (x\notin C)] \or [(x\in A) \and (x\in B) \and (x\notin A)]](/images/math/5/f/c/5fcc49e93a43d72a27f2ce5b2d9a7dc2.png)
בצד הימני הוספנו סתירה בעזרת הקשר "או" ולכן נשארנו עם ביטוי שקול. כעת נשתמש בחוק הפילוג של הלוגיקה:
![\iff [(x\in A) \and (x\in B)]\and [(x\notin C)\or(x\notin A)]\iff [(x\in A) \and (x\in B)]\and \neg [(x\in C)\and(x\in A)]](/images/math/e/f/8/ef804662c2efab381fbe719261ae3d1f.png)
וזה בדיוק מה שרצינו.
דרך הכלה דו כיוונית:
(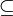 ) נניח
) נניח 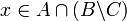 אזי
אזי
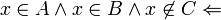
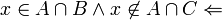
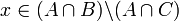
(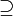 ) נניח
) נניח 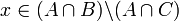 אזי
אזי
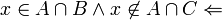
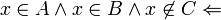 (כי אם
(כי אם 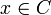 אזי
אזי 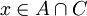 סתירה)
סתירה)
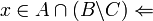
תרגיל
נתונות 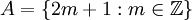 , ו
, ו 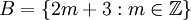 . הוכח שA=B.
. הוכח שA=B.
פתרון
נוכיח הכלה דו כיוונית. נניח  לכן קיים מספר שלם m כך ש
לכן קיים מספר שלם m כך ש 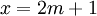 . קל לראות שמתקיים
. קל לראות שמתקיים 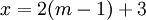 אבל אז מכיוון ש m-1 הינו מספר שלם מתקיים
אבל אז מכיוון ש m-1 הינו מספר שלם מתקיים 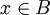 כפי שרצינו.
כפי שרצינו.
ההכלה בכיוון ההפוך דומה.
משלים
הגדרה: תהי קבוצה U (אוניברסלית) ותהי תת קבוצה שלה 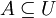 . נגדיר את המשלים של A (ביחס ל
. נגדיר את המשלים של A (ביחס ל 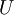 להיות:
להיות:
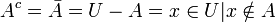
תכונות בסיסיות:
על המשלימים מתקיימים חוקי דה מורגן (הנובעים ישירות מחוקי דה מורגן בלוגיקה):
הערה: באופן כללי מתקיים
א. 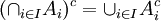
ב. 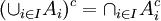
הוכחה לסעיף א:
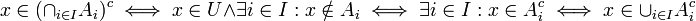
תרגיל
הוכיחו: 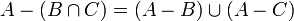
פתרון
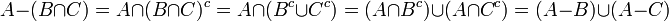
קבוצת החזקה
הגדרה: תהי קבוצה A. נגדיר את קבוצת החזקה של A בתור אוסף כל תתי הקבוצות של A. מסומן 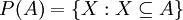
דוגמא:
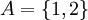 אזי
אזי 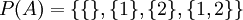 .
.
האם אתם יכולים למנות כמה איברים יש בקבוצת החזקה?
תרגיל ממבחן
יהיו A,B,C קבוצות. הוכיחו/הפריכו:
א. אם 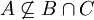 אזי
אזי 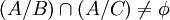
ב. אם 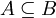 אזי
אזי 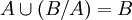
ג. אם 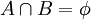 אזי
אזי 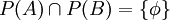
פתרון
א. הפרכה: 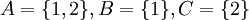 . אזי ברור שA איננה מוכלת בחיתוך של B וC אבל
. אזי ברור שA איננה מוכלת בחיתוך של B וC אבל 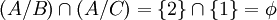
ב. נתון שלכל 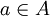 מתקיים
מתקיים 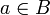 . אזי
. אזי ![x\in [A\cup(B/A)] \iff (x\in A) \or [(x\in B)\and (x\notin A)] \iff [(x\in A) \or (x\in B)] \and [(x \in A)\or (x\notin A)]](/images/math/f/8/a/f8a74cc645180bad23b7a6f990e383e0.png)
כעת, הצד הימני הוא טאוטולוגיה וניתן להסיר אותו. מכיוון שנתון  ניתן להסיק בקלות ש
ניתן להסיק בקלות ש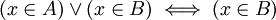 כפי שרצינו.
כפי שרצינו.
דרך נוספת: נגדיר את B להיות הקבוצה האוניברסאלית 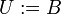 ואז צריך להוכיח כי
ואז צריך להוכיח כי
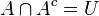 וזה אכן נכון!
וזה אכן נכון!
ג. נניח בשלילה ש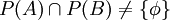 . מכיוון שהקבוצה הריקה שייכת לכל קבוצת חזקה החיתוך אינו ריק. לכן לפי הנחת השלילה קיימת קבוצה לא ריקה
. מכיוון שהקבוצה הריקה שייכת לכל קבוצת חזקה החיתוך אינו ריק. לכן לפי הנחת השלילה קיימת קבוצה לא ריקה 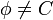 השייכת לחיתוך
השייכת לחיתוך 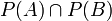 . קבוצות החזקה הן אוסף תתי הקבוצות, ולכן
. קבוצות החזקה הן אוסף תתי הקבוצות, ולכן 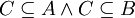 . מכיוון שC אינה ריקה קיים בה איבר
. מכיוון שC אינה ריקה קיים בה איבר 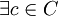 וקל מאד לראות ש
וקל מאד לראות ש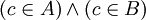 ולכן c מוכל בחיתוך בסתירה לכך שהחיתוך ריק.
ולכן c מוכל בחיתוך בסתירה לכך שהחיתוך ריק.