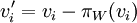הבדלים בין גרסאות בדף "88-113 לינארית 2 סמסטר א תשעג/תרגילים/8"
מתוך Math-Wiki
(יצירת דף עם התוכן "==1== תהי <math>A\in\mathbb{C}^{n\times n}</math> המקיימת <math>A=A^*</math>. הוכיחו כי <math>N(A)=N(A^2)</math> (רמז: השתמשו במכפל...") |
(←3) |
||
| שורה 12: | שורה 12: | ||
==3== | ==3== | ||
| + | יהי V ממ"פ ממימד n, ויהי W תת מרחב של V מימד k. | ||
| + | ===א=== | ||
| + | יהי <math>B=\{w_1,...,w_k\}</math> בסיס א"נ ל W. | ||
| + | |||
| + | יהיו <math>v_{k+1},...,v_n</math> המשלימים את הבסיס B להיות בסיס למרחב V. | ||
| + | |||
| + | |||
| + | לכל <math>k+1\leq i \leq n</math> נסמן: | ||
| + | |||
| + | ::<math>v'_i=v_i-\pi_W(v_i)</math> | ||
| + | |||
| + | |||
| + | הוכיחו כי <math>\{w_1,...,w_k,v'_{k+1},...,v'_n\}</math> בסיס ל V | ||
| + | |||
| + | ===ב=== | ||
| + | הוכיחו את משפט הפירוק הניצב <math>W\oplus W^\perp=V</math> | ||
| + | |||
| + | ===ג=== | ||
| + | |||
| + | מצאו את צורת הז'ורדן של אופרטור ההיטל <math>\pi_W</math> | ||
| + | |||
| + | ==4== | ||
גרסה מ־18:39, 26 בדצמבר 2012
1
תהי 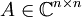 המקיימת
המקיימת 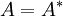 . הוכיחו כי
. הוכיחו כי 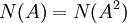
(רמז: השתמשו במכפלה הפנימית הסטנדרטית בדומה למה שראינו בתרגול)
2
תהי 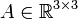 מטריצה אוניטרית המקיימת
מטריצה אוניטרית המקיימת 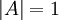 .
.
הוכיחו כי 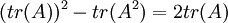
(רמז: מה עשויים להיות הע"ע של A?)
3
יהי V ממ"פ ממימד n, ויהי W תת מרחב של V מימד k.
א
יהי 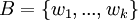 בסיס א"נ ל W.
בסיס א"נ ל W.
יהיו 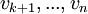 המשלימים את הבסיס B להיות בסיס למרחב V.
המשלימים את הבסיס B להיות בסיס למרחב V.
לכל 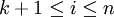 נסמן:
נסמן:
הוכיחו כי 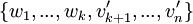 בסיס ל V
בסיס ל V
ב
הוכיחו את משפט הפירוק הניצב 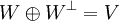
ג
מצאו את צורת הז'ורדן של אופרטור ההיטל