הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מדמח/פתרון בוחן 2"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏2)
(←‏2)
שורה 25: שורה 25:
  
 
<math>a_n=(-1)^n\frac{1}{\sqrt{n}}</math> מתכנס לפי לייבניץ, אבל <math>a_n^2=\frac{1}{n}</math> מתבדר
 
<math>a_n=(-1)^n\frac{1}{\sqrt{n}}</math> מתכנס לפי לייבניץ, אבל <math>a_n^2=\frac{1}{n}</math> מתבדר
 +
 +
==3==
 +
===א===
 +
[[88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/טורים/מבחנים לחיוביים/דוגמאות/7|פתרון]]
 +
 +
===ב===
 +
 +
<math>2^n+(-1)^n2^n\leq 2\cdot 2^n</math>
 +
 +
ולכן סה"כ הטור קטן מהטור ההנדסי המתכנס
 +
 +
<math>2\sum (\frac{2}{3})^n</math>
 +
 +
ולכן מתכנס
 +
 +
 +
===ג===
 +
[[88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/טורים/מבחנים לחיוביים/דוגמאות/8|פתרון]]
 +
 +
 +
===ד===
 +
 +
[[88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/טורים/מבחנים לחיוביים/דוגמאות/4|פתרון]]
 +
 +
===ה===

גרסה מ־17:59, 4 בפברואר 2012

1

תנאי הכרחי להתכנסות הטור 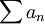\sum a_nהוא התכנסות הסדרה לאפס 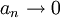a_n\rightarrow 0. תנאי זה הכרחי אבל אינו מספיק.


טור מתכנס בתנאי הינו טור המתכנס, אבל אינו מתכנס בהחלט.

2

א

ברור כי 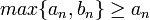max\{a_n,b_n\}\geq a_n ולכן לפי מבחן ההשוואה הראשון לטורים חיוביים הטור מתבדר.

ב

כיוון שהטור 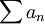\sum a_n מתכנס, אזי הסדרה שלו שואפת לאפס. לכן

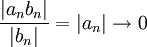
\frac{|a_nb_n|}{|b_n|}=|a_n|\rightarrow 0

ולכן לפי מבחן ההשוואה השני לטורים חיוביים, הטור 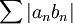\sum |a_nb_n| מתכנס, כלומר הטור 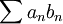\sum a_nb_n מתכנס בהחלט.

ג

הוכחה:

כיוון שהטור 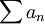\sum a_n מתכנס, אזי הסדרה שלו שואפת לאפס. לכן הסדרה 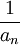\frac{1}{a_n}לא חסומה או לא מוגדרת ובכל מקרה אינה שואפת לאפס ולכן הטור 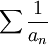\sum\frac{1}{a_n} מתבדר.

ד

הפרכה:

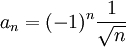a_n=(-1)^n\frac{1}{\sqrt{n}} מתכנס לפי לייבניץ, אבל 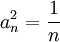a_n^2=\frac{1}{n} מתבדר

3

א

פתרון

ב

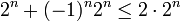
2^n+(-1)^n2^n\leq 2\cdot 2^n

ולכן סה"כ הטור קטן מהטור ההנדסי המתכנס

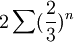
2\sum (\frac{2}{3})^n

ולכן מתכנס


ג

פתרון


ד

פתרון

ה

מקור: https://math-wiki.com/index.php?title=88-132_אינפי_1_סמסטר_א%27_תשעב/מדמח/פתרון_בוחן_2&oldid=19381