הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/טורים/מבחנים לחיוביים/דוגמאות/2"

גרסה מ־08:51, 20 בפברואר 2012

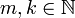
נפעיל את מבחן המנה (דלאמבר):

\lim \frac{a_{n+1}}{a_n} = \lim \frac{\sqrt[m]{(n+1)!}}{\sqrt[k]{(2(n+1))!}}\cdot\frac{\sqrt[k]{(2n)!}}{\sqrt[m]{n!}}=

=\lim\frac{\sqrt[m]{n+1}}{\sqrt[k]{(2n+1)(2n+2)}}=\lim\frac{\sqrt[m]{n}}{\sqrt[k]{4n^2}}\cdot \frac{\sqrt[m]{1+\frac{1}{n}}}{\sqrt[k]{1+\frac{3}{2n}+\frac{1}{2n^2}}}

הביטוי הימני שואף לאחד, לכן מספיק לנו לחשב את הגבול:

\lim\frac{\sqrt[m]{n}}{\sqrt[k]{4n^2}}=\frac{n^{\frac{1}{m}-\frac{2}{k}}}{\sqrt[k]{4}}

נחלק למקרים:

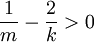\frac{1}{m}-\frac{2}{k}>0

(כלומר

2m<k

)

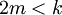אזי

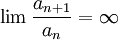$\lim \frac{a_{n+1}}{a_n}=\infty$ והטור מתבדר

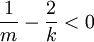\frac{1}{m}-\frac{2}{k}<0

(כלומר

2m>k

)

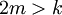אזי

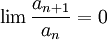$\lim \frac{a_{n+1}}{a_n}=0$ והטור מתכנס

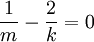\frac{1}{m}-\frac{2}{k}=0

(כלומר

2m=k

)

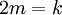אזי

לכל k, מתקיים $\lim \frac{a_{n+1}}{a_n}=\frac{1}{\sqrt[k]{4}}<1$ ולכן הטור מתכנס.

@@ שורה 11: / שורה 11: @@
 ::<math>=\lim\frac{\sqrt[m]{n+1}}{\sqrt[k]{(2n+1)(2n+2)}}=\lim\frac{\sqrt[m]{n}}{\sqrt[k]{4n^2}}\cdot
-\frac{\sqrt[m]{1+\frac{1}{n}}}{\sqrt[k]{1+\frac{6}{n}+\frac{2}{n^2}}}
+\frac{\sqrt[m]{1+\frac{1}{n}}}{\sqrt[k]{1+\frac{3}{2n}+\frac{1}{2n^2}}}
 </math>