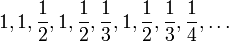88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/סדרות/תתי סדרות
תתי-סדרות
תת-סדרה מתקבלת מסדרה ע"י השמטת מספר כלשהו של אברים (לא בהכרח סופי). נגדיר זאת במדויק:
- הגדרה.
תהי סדרה ממשית  ותהי סדרה עולה ממש של מספרים טבעיים
ותהי סדרה עולה ממש של מספרים טבעיים 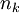 (כלומר
(כלומר 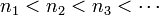 ). אזי
). אזי 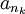 הנה תת-סדרה של
הנה תת-סדרה של  .
.
הערה: שימו לב שמכיון שההגדרה המדויקת של סדרה הנה פונקציה, תת-סדרה הנה הרכבה של פונקציית הסדרה על פונקציה המשמיטה אברים מהסדרה (בפרט, את כל האברים שבין 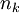 לבין
לבין 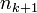 לכל
לכל  ).
).
דוגמא. נביט בסדרה 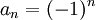 ובסדרת המספרים הטבעיים
ובסדרת המספרים הטבעיים 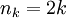 אזי
אזי 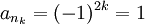 הנה תת-סדרה של הסדרה המקורית.
הנה תת-סדרה של הסדרה המקורית.
דוגמא. נביט בסדרה 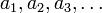 אזי תת-סדרה אחת שלה תהא
אזי תת-סדרה אחת שלה תהא 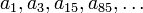
- הגדרה.
תהא  סדרה. אזי
סדרה. אזי  נקרא גבול חלקי של הסדרה אם קיימת לה תת-סדרה
נקרא גבול חלקי של הסדרה אם קיימת לה תת-סדרה 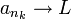 .
.
- משפט.
תהא  סדרה. אזי
סדרה. אזי  גבול חלקי שלה אם"ם לכל
גבול חלקי שלה אם"ם לכל  ולכל
ולכל 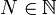 קיים
קיים 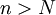 כך ש-
כך ש- 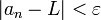 .
.
במילים, קיימים אינסוף אברים מהסדרה הקרובים לגבול כרצוננו, אך לא כל האברים חייבים להתקרב לגבול כרצוננו (אחרת הוא היה גבול מלא ולא חלקי).
- משפט.
סדרה מתכנסת לגבול  אם"ם כל תתי-הסדרות שלה מתכנסות לגבול
אם"ם כל תתי-הסדרות שלה מתכנסות לגבול  .
.
מסקנה. אם לסדרה קיימת תת-סדרה המתכנסת לגבול  וקיימת תת-סדרה שאינה מתכנסת לגבול
וקיימת תת-סדרה שאינה מתכנסת לגבול  אזי הסדרה המקורית אינה מתכנסת.
אזי הסדרה המקורית אינה מתכנסת.
- משפט בולצאנו ויירשטראס.
לכל סדרה חסומה יש תת-סדרה מתכנסת.
הוכחה. (בהוכחה מוזכרת גם הלמה של קנטור.)
- משפט.
תהי  סדרה המתכנסת לגבול
סדרה המתכנסת לגבול  . אזי כל תת-סדרה שלה מתכנסת לגבול
. אזי כל תת-סדרה שלה מתכנסת לגבול  .
.
- הוכחה.
לפי הגדרת הגבול, לכל  יש מקום בסדרה שהחל ממנו והלאה אברי הסדרה קרובים לגבול עד כדי
יש מקום בסדרה שהחל ממנו והלאה אברי הסדרה קרובים לגבול עד כדי  . כיון שאברי תת-הסדרה נלקחים מהסדרה המקורית ללא שינוי סדר הקדימות, גם אבריה קרובים לגבול עד כדי
. כיון שאברי תת-הסדרה נלקחים מהסדרה המקורית ללא שינוי סדר הקדימות, גם אבריה קרובים לגבול עד כדי  החל ממקום מסוים והלאה. (שימו לב שהמקום הזה מגיע יותר מהר מאשר בסדרה המקורית כיון שאולי זרקנו אברים בדרך.)
החל ממקום מסוים והלאה. (שימו לב שהמקום הזה מגיע יותר מהר מאשר בסדרה המקורית כיון שאולי זרקנו אברים בדרך.)
- תרגיל.
מצא את כל הגבולות החלקיים של הסדרה 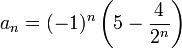
- פתרון
נביט בתת הסדרה המורכבת מהאברים הזוגיים 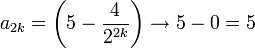
באופן דומה סדרת האי-זוגיים שואפת ל- 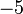 . האם
. האם 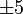 הם הגבולות החלקיים היחידים של הסדרה?
הם הגבולות החלקיים היחידים של הסדרה?
נניח בשלילה שהיה גבול חלקי אחר. לפי ההגדרה, קיימת תת-סדרה השואפת אליו. בהכרח היו בתת-סדרה זו אינסוף אברים זוגיים או אינסוף אברים אי-זוגיים. נביט בתת-הסדרה המורכבת מאינסוף אברים אילו בתוך תת-הסדרה. מצד אחד הם שואפים ל- 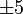 כי הם מהווים תת-סדרה של האברים הזוגיים או האי-זוגיים, אבל מצד שני הם שואפים לגבול החלקי האחר מכיון שהם מהווים תת-סדרה של תת-הסדרה המתכנסת אליו, בסתירה.
כי הם מהווים תת-סדרה של האברים הזוגיים או האי-זוגיים, אבל מצד שני הם שואפים לגבול החלקי האחר מכיון שהם מהווים תת-סדרה של תת-הסדרה המתכנסת אליו, בסתירה.
- דוגמא.
לסדרה הבאה, אינסוף גבולות חלקיים:
- תרגיל.
מצא סדרה שקבוצת הגבולות החלקיים שלה מהווה את כל המספרים הממשיים.
- פתרון
נסדר את קבוצת המספרים הרציונאליים  . כיון שבכל סביב של מספר ממשי ישנו מספר רציונאלי, ניתן לבנות סדרת מספרים רציונאליים השואפת אליו. בנוסף, ברור כי יש תתי-סדרות השואפות לפלוס ומינוס אינסוף.
. כיון שבכל סביב של מספר ממשי ישנו מספר רציונאלי, ניתן לבנות סדרת מספרים רציונאליים השואפת אליו. בנוסף, ברור כי יש תתי-סדרות השואפות לפלוס ומינוס אינסוף.
בכוונה לא ניסחנו את הפתרון באופן פורמלי ומדויק, עשו את זה בעצמכם כתרגיל.