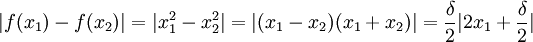88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/פונקציות/רציפות במ"ש
רציפות במידה שווה
עד כה הגדרנו רציפות באופן נקודתי ואמרנו שפונקציה רציפה בקטע אם היא רציפה בכל נקודה בקטע בנפרד.
באופן אינטואיטיבי, אומרים כי פונקציה מתכנסת 'יותר מהר' אל הגבול שלה, אם הדלתא הנדרש לאפסילון הוא גדול יותר (כלומר הפונקציה קרובה לגבול בתחום יותר רחב). אנו רוצים להגדיר פונקציות אשר מהירות ההתכנסות שלהן דומה בכל נקודה בקטע מסויים.
הגדרה.
פונקציה f נקראת רציפה במידה שווה (רציפה במ"ש) בקטע A אם:
- לכל
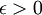 קיים
קיים 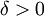 כך שלכל זוג נקודות
כך שלכל זוג נקודות 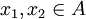 המקיימות
המקיימות 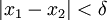 מתקיים
מתקיים 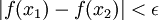
שימו לב כי ברציפות רגילה בקטע A, לכל נקודה בקטע ההתאמה של הדלתא לאפסילון עשוייה להיות שונה. כאשר הפונקציה רציפה במ"ש, לכל אפסילון יש דלתא המתאים לכל הקטע A.
הערה: ברור שאם פונקציה רציפה במ"ש על קטע A, היא גם רציפה במ"ש על כל קטע המוכל ב-A.
דוגמאות.
נבחן את הפונקציה 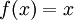 , ונוכיח כי היא רציפה במ"ש על כל ציר הממשיים.
, ונוכיח כי היא רציפה במ"ש על כל ציר הממשיים.
אכן, לכל אפסילון ניקח דלתא שווה לאפסילון ונקבל כי 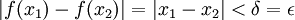
בדוגמא הבאה נלמד כי פונקציה מסויימת עשוייה להיות רציפה במ"ש בקטע מסויים אך לא רציפה במ"ש בקטע אחר. כפי שנראה בהמשך, כל פונקציה הרציפה על קטע סופי וסגור רציפה בו במ"ש, ואילו ישנן פונקציות רציפות שאינן רציפות במ"ש על כל ציר הממשיים.
ראשית, נביט ב 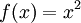 על הקטע הסופי
על הקטע הסופי 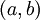 . יהי אפסילון גדול מאפס, אזי:
. יהי אפסילון גדול מאפס, אזי:
כעת, אם ניקח 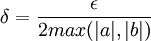 נקבל את הדרוש.
נקבל את הדרוש.
עכשיו, נבחן את אותה הפונקציה 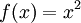 על כל הממשיים, ונוכיח כי היא אינה רציפה שם במ"ש.
על כל הממשיים, ונוכיח כי היא אינה רציפה שם במ"ש.
ניקח 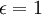 . צריך להוכיח כי לכל
. צריך להוכיח כי לכל 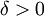 קיים זוג מספרים ממשיים המקיימים
קיים זוג מספרים ממשיים המקיימים 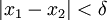 וגם
וגם 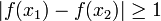 .
.
ניקח 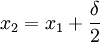 ונראה כי אם נבחר את
ונראה כי אם נבחר את 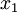 להיות גדול מספיק, נקבל את הדרוש. ברור כי
להיות גדול מספיק, נקבל את הדרוש. ברור כי 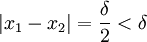
ברור שאם נגדיל את 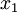 מספיק נקבל את הדרוש.
מספיק נקבל את הדרוש.
מבחנים לבדיקה האם פונקציה רציפה במ"ש
משפט
פונקציה הרציפה במ"ש על קטע רציפה שם.
משפט
תהי f פונקציה רציפה על קטע לאו דווקא סופי, אזי אם הגבולות של הפונקציה בקצות הקטע קיימים וסופיים, הפונקציה רציפה במ"ש בקטע (ההפך אינו נכון בהכרח, שכן ראינו את הפונקציה 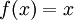 שאין לה גבול באינסוף, אך היא רציפה במ"ש על כל ציר הממשיים.)
שאין לה גבול באינסוף, אך היא רציפה במ"ש על כל ציר הממשיים.)
הוכחה.
נחלק את ההוכחה לשנים- כאשר קצה הקטע הוא סופי, וכאשר הוא אינסופי. ההוכחות לימין ולשמאל דומות, לכן נוכיח ב.ה.כ לקצה הקטע הימני.