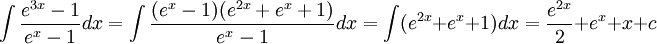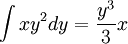88-133 אינפי 2 תשעב סמסטר ב/הרצאה 2 (6/3/12)
מתוך Math-Wiki
הרצאה 2 (6/3/12)
שני כללים פשוטים:
1) ![\int [f(x)+g(x)]dx=\int f(x)dx+\int g(x)dx](/images/math/7/8/b/78bced3f47d229501a8c086270b1edb6.png) .
.
2) 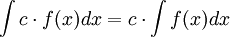 . (עבור
. (עבור 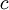 קבוע)
קבוע)
דוגמאות
1) 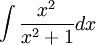
2) 
3) 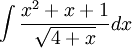
4) 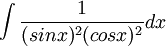
- דרך נוספת:
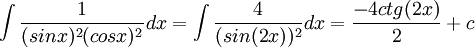
- התוצאות נראות שונות. אין הן זהות טריגונומטרית, אך הן שונות עד לכדי קבוע (c)
5) 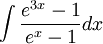
6) 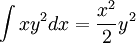
אינטגרציה בחלקים:
נתחיל בנוסחה הידועה ![[f(x)g(x)]'=f(x)g'(x)+f'(x)g(x)](/images/math/e/0/1/e0110ecd5a91efb6a405dea79c1e3219.png) , לכן:
, לכן: ![\int [f(x)g'(x)+f'(x)g(x)]dx=f(x)g(x)](/images/math/f/4/6/f466b299429f8a4e35b536448e1da974.png) לאחר העברת אגפים נגיע לנוסחה לאינטגרציה בחלקים:
לאחר העברת אגפים נגיע לנוסחה לאינטגרציה בחלקים:
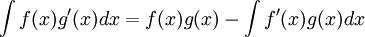
דוגמאות
1) 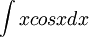
- נבחר
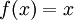 ו
ו 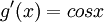
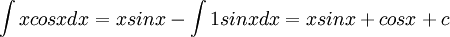
2) 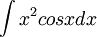
- נבחר
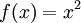 ו
ו 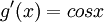
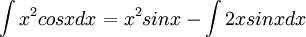
- נשתמש שוב באינטגרציה בחלקים - נגדיר:
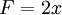 ו
ו 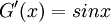
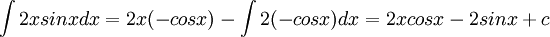
- ולכן התוצאה הסופית
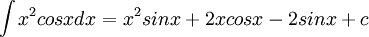
3) 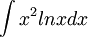
- לא מומלץ לבחור
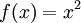 ו
ו 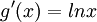 , כי מיד נצטרך למצוא את
, כי מיד נצטרך למצוא את 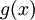 שהיא הפונקציה הקדומה של
שהיא הפונקציה הקדומה של 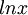 , ועוד לא חישבנו אותה.
, ועוד לא חישבנו אותה.
שיטת ההצבה: (או החלפת משתנים)
נתחיל עם כלל השרשרת: 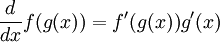 .
.
לכן אם 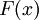 קדומה ל-
קדומה ל- :
: 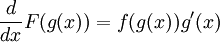 ומזה נובע:
ומזה נובע: 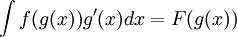 .
.
כעת, הדרך הפורמלית למציאת האינטגרל: אם נתון 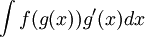 נסמן
נסמן 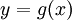 ולכן
ולכן 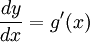 . פעולה פורמלית:
. פעולה פורמלית: 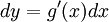 . כעת נציב את מה שסימנו:
. כעת נציב את מה שסימנו:
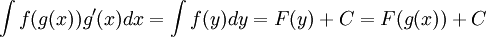 (לא לשכוח בסוף להציב בחזרה את
(לא לשכוח בסוף להציב בחזרה את  !!!)
!!!)
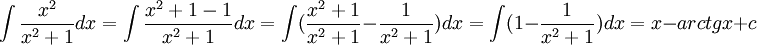
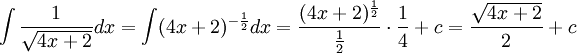
![\int \frac{x^{2}+x+1}{\sqrt{4+x}}dx=\int \frac{[(x+4)-4)]^{2}+[(x+4)-4]+1}{\sqrt{4+x}}dx=\int \frac{(x+4)^{2}-8(x+4)+16+(x+4)-4+1}{\sqrt{x+4}}dx=\int \frac{(x+4)^{2}-7(x+4)+13}{\sqrt{x+4}}dx=\int [(x+4)^{\frac{3}{2}}-7(x+4)^{\frac{1}{2}}+13(x+4)^{-\frac{1}{2}}]dx=\frac{(x+4)^{\frac{5}{2}}}{\frac{5}{2}}-7\frac{(x+4)^{\frac{3}{2}}}{\frac{3}{2}}+13\frac{(x+4)^{\frac{1}{2}}}{\frac{1}{2}}+c](/images/math/e/b/9/eb9bdef93aa6ee301112f1ced337b2de.png)
![\int \frac{1}{(sinx)^{2}(cosx)^{2}}dx=\int \frac{(sinx)^{2}+(cosx)^{2}}{(sinx)^{2}(cosx)^{2}}dx=\int [\frac{(sinx)^{2}}{(sinx)^{2}(cosx)^{2}}+\frac{(cosx)^{2}}{(sinx)^{2}(cosx)^{2}}]dx=\int [\frac{1}{(cosx)^{2}}+\frac{1}{(sinx)^{2}}]dx=tgx-ctgx+c](/images/math/8/b/e/8bef1c2b83d00362f4bd1f36384bf9d7.png)