88-133 אינפי 2 תשעב סמסטר ב/תרגילים/תרגיל 3/פתרון
1
ראו פתרון בקישור הבא (תרגיל מס' 3): פתרון
2
ראו פתרון בקישור הבא (תרגיל מס' 4): פתרון
3
ראו פתרון בקישור הבא (תרגיל מס' 7): פתרון
4
ראו פתרון בקישור הבא (תרגיל מס' 8): פתרון
5
(זה לא לקוח מתרגילי בית קודמים!)
אם מישהו יכול לעבור על זה ולראות שהכל כשורה יהיה זה נחמד.
נראה קודם כי הפונקציה f קעורה לפי התנאי הנתון (אני לא בטוח שהחלק הזה הכרחי, אבל למה לא?).
f קעורה  עבור כל שתי נקודות בקטע, הישר המחבר בין הנקודות נמצא תחת גרף הפונקציה.
עבור כל שתי נקודות בקטע, הישר המחבר בין הנקודות נמצא תחת גרף הפונקציה.
הוכחה (טענה)
יהיו ![x_{1},x_{2}\in [0,2]](/images/math/0/6/3/0636913a7d16c10e344d4c00d2846902.png) , ונניח בה"כ
, ונניח בה"כ 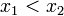 .
.
משוואות הישר העובר בין שתי הנקודות היא: 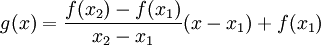
תהי ![y\in [x_{1},x_{2}]](/images/math/8/6/7/8678e8f1e192208306455d0bfd3c5a5c.png) , נקודה בקטע בין שתי הנקודות, נרצה להראות כי
, נקודה בקטע בין שתי הנקודות, נרצה להראות כי 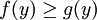 (וזה אומר שהישר מתחת לגרף הפונקציה).
(וזה אומר שהישר מתחת לגרף הפונקציה).
קיים ![t\in [0,1]](/images/math/d/9/a/d9a06fde4663cdd5b1ba693e9127232f.png) שעבורו:
שעבורו: 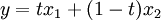 , כעת נציב את
, כעת נציב את  במשוואת הישר g.
במשוואת הישר g.
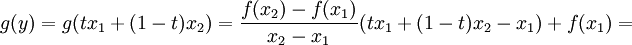
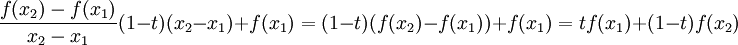
ולפי הנתון שנתון לנו, נקבל כי:
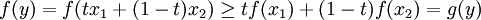 .
.
מה שרצינו להוכיח.
בחזרה לתרגיל
ואם נחזור להוכחה המקורית, אז הפונקציה f נמצאת מעל הישר שמחבר את הנק': 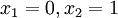 בקטע
בקטע ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) .
.
וכן הפונקציה f נמצאת מעל הישר שמחבר את הנק': 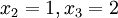 בקטע
בקטע ![[1,2]](/images/math/f/7/9/f79408e5ca998cd53faf44af31e6eb45.png) .
.
כל הישרים המחברים את הנקודות 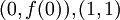 נמצאים מעל הישר
נמצאים מעל הישר  בקטע
בקטע ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png)
כל הישרים המחברים את הנקודות 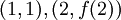 נמצאים מעל הישר
נמצאים מעל הישר 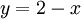 בקטע
בקטע ![[1,2]](/images/math/f/7/9/f79408e5ca998cd53faf44af31e6eb45.png)
(תוכיחו את זה אם בא לכם, זה באמת לא קשה)
ובסה"כ מתקיים: ![f(x)\geq h(x)=\begin{cases}
x & \text{ if } x\in[0,1] \\
2-x & \text{ if } x\in [1,2]
\end{cases}](/images/math/8/b/0/8b0f794dfc158048d495636214cffc7d.png)
ומכיוון ששתי הפונקציות אי שליליות, אז לפי משפט: 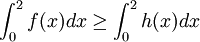
אבל את האינטגרל של 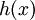 קל לחשב ומתקבל:
קל לחשב ומתקבל: 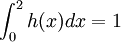
ולכן סיימנו (:.
הערה: אפשר גם סתם לראות ש 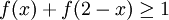 ולהשתמש בהשוואת אינטגרלים.
ולהשתמש בהשוואת אינטגרלים.
- אתה בטוח שזה נכון? אם מסתכלים נניח על
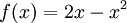 זה לא נכון עבור כל x.
זה לא נכון עבור כל x.