88-611 אנליזה 1 למורים סמסטר א תשעו/מערכי תרגול/שיעור 2
תוכן עניינים
- 1 סדרות
- 1.1 הגדרה
- 1.2 דוגמאות
- 1.3 הגדרה (סביבת ה-אפסילון של הנקודה)
- 1.4 הגדרה (גבול של סדרה)
- 1.5 דוגמאות
- 1.6 תרגיל:
- 1.7 פתרון:
- 1.8 תנאי הכרחי ומספי לאי קיום הגבול
- 1.9 תרגיל:
- 1.10 פתרון:
- 1.11 הגדרה
- 1.12 דוגמאות לסדרות מתבדרות
- 1.13 הערות
- 1.14 הגדרות
- 1.15 לדוגמה
- 1.16 טכניקות בסיסיות לחישוב כבולות
- 1.17 טענה (כלל המנה)
- 1.18 תרגיל
- 1.19 פתרון
- 1.20 טענה:
- 1.21 תרגיל
- 1.22 פתרון
- 1.23 הערה
- 1.24 כפל במספר צמוד
סדרות
הגדרה
סדרה של מספרים ממשיים היא פונקציה 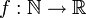 שלכל
שלכל 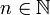 מתאימה מספר ממשי
מתאימה מספר ממשי 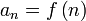 שנקרא האיבר ה-n-י של הסדרה.
שנקרא האיבר ה-n-י של הסדרה.
סדרה היא רשימה אינסופית מסודרת של מספרים ממשיים: 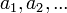 שנסמנה
שנסמנה 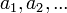 , והמספר ה-n נקרא האינדקס של האיבר
, והמספר ה-n נקרא האינדקס של האיבר 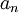 .
.
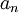 נקרא האיבר הכללי של הסדרה ואם הוא נתון על ידי נוסחה אלגברית אזי הביטוי
נקרא האיבר הכללי של הסדרה ואם הוא נתון על ידי נוסחה אלגברית אזי הביטוי 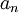 נקרא הנוסחה האלגברית של הסדרה.
נקרא הנוסחה האלגברית של הסדרה.
דוגמאות
1) הסדרה 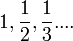 נקראת הסדרה ההרמונית. נוסחת האיבר הכללי שלה היא שלה
נקראת הסדרה ההרמונית. נוסחת האיבר הכללי שלה היא שלה 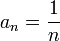 .
.
2) אם 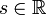 הסדרה
הסדרה 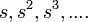 נקראת הסדרה ההנדסית עם בסיס s ואיברה הכללי הוא
נקראת הסדרה ההנדסית עם בסיס s ואיברה הכללי הוא 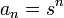 .
.
3) הסדרה s,s,s,s... נקראת הסדרה הקבועה ונסמנה הסדרה הקבועה שערכה s ונסמנה 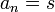 .
.
הגדרה (סביבת ה-אפסילון של הנקודה)
יהי 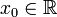 ויהי
ויהי  , סביבת ה-אפסילון של
, סביבת ה-אפסילון של 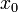 שמסומנת ב-
שמסומנת ב- 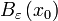 ומוגדרת ע"י
ומוגדרת ע"י 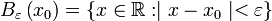 . כדאי לחשוב על
. כדאי לחשוב על 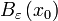 כקבוצת הנקודות שמרחקם מ-
כקבוצת הנקודות שמרחקם מ-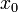 קטן מ-
קטן מ- .
.
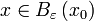 אם ורק אם
אם ורק אם 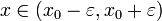 .
.
הגדרה (גבול של סדרה)
תהי 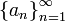 סדרה נתונה. נאמר שמספר L הוא גבול של סדרה
סדרה נתונה. נאמר שמספר L הוא גבול של סדרה 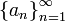 אם לכל
אם לכל  קטן ככל שיהיה קיים מספר טבעי
קטן ככל שיהיה קיים מספר טבעי 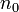 כך שלכל
כך שלכל 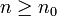 מתקיים
מתקיים 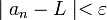 .
.
במילים: לכל  יש לכל היותר מספר סופי של איברי הסדרה שאינם נמצאים בתוך הסביבה
יש לכל היותר מספר סופי של איברי הסדרה שאינם נמצאים בתוך הסביבה 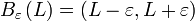 . (במילים אחרות החל ממקום
. (במילים אחרות החל ממקום 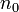 כל איברי הסדרה יהיו בתוך הסביבה
כל איברי הסדרה יהיו בתוך הסביבה 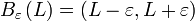 של L).
של L).
אם L הוא גבול של סדרה 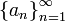 אז נרשום
אז נרשום 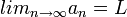 או
או 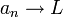 .
.
אם לסדרה יש גבול נאמר שהסדרה מתכנסת (או שואפת לגבול זה), אם אין לסדרה גבול נאמר שהיא מתבדרת.
דוגמאות
1) הסדרה 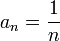 מתכנסת לגבול L=0, או בקיצור
מתכנסת לגבול L=0, או בקיצור 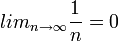 .
.
הוכחה: נוכיח ש-0 הוא באמת הגבול של הסדרה לפי ההגדרה של הגבול
יהי  , רוצים להוכיח שקיים מקום בסדרה שנסמנו ב-
, רוצים להוכיח שקיים מקום בסדרה שנסמנו ב-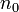 כל שהחל מהמקום הזה כלומר עבור כל
כל שהחל מהמקום הזה כלומר עבור כל 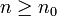 מתקיים
מתקיים 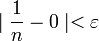 .
.
מתקיים 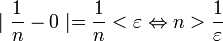 ולכן אם נבחר
ולכן אם נבחר 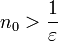 נקבל
נקבל 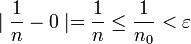 .
.
2) אם 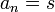 הסדרה הקבועה ולכן הגבול שלה הוא
הסדרה הקבועה ולכן הגבול שלה הוא 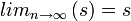 .
.
3) לכל 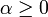
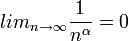 .
.
תרגיל:
מצא את גבול הסדרה 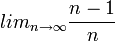 והוכח לפי ההגדרה שזה באמת הגבול.
והוכח לפי ההגדרה שזה באמת הגבול.
פתרון:
ולכן נסיק שהגבול הוא 1.
יהיה  , רוצים להוכיח שקיים
, רוצים להוכיח שקיים 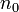 כך שלכל
כך שלכל 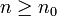 מתקיים
מתקיים 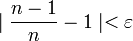 .
.
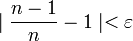 אם ורק אם
אם ורק אם 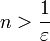 ולכן כמו מקודם מבחר
ולכן כמו מקודם מבחר 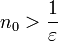 כך שלכל
כך שלכל 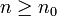 מתקיים
מתקיים 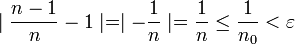 .
.
תנאי הכרחי ומספי לאי קיום הגבול
המספר L איננו הגבול של הסדרה של 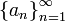 אם קיים
אם קיים 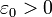 כך שלכל
כך שלכל 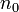 קיים
קיים 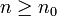 כך שמתקיים
כך שמתקיים 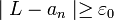 .
.
במילים:הסדרה 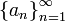 אינה מתכנסת לגבול L אם ורק אם קיים
אינה מתכנסת לגבול L אם ורק אם קיים 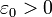 מסויים כך שאינסוף מאיברי הסדרה נמצאים מחוץ לסביבה
מסויים כך שאינסוף מאיברי הסדרה נמצאים מחוץ לסביבה 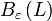 .
.
תרגיל:
הוכח כי 2 אינו הגבול של 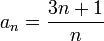 .
.
פתרון:
עלינו למצוא 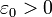 מסויים כל שלכל
מסויים כל שלכל 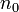 טבעי קיים
טבעי קיים 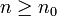 כך שיתקיים
כך שיתקיים 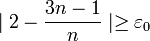 .
.
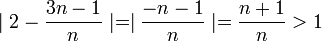 קיבלנו שמרחק בין 2 לבין כל אחד מאיברי הסדרה הוא יותר גדול מ-1 ולכן אם נבחר
קיבלנו שמרחק בין 2 לבין כל אחד מאיברי הסדרה הוא יותר גדול מ-1 ולכן אם נבחר 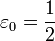 לא נוכל למצוא אף
לא נוכל למצוא אף 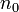 שעבורו כמעט כל איברי הסדרה יהיו בסביבה
שעבורו כמעט כל איברי הסדרה יהיו בסביבה 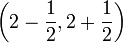 .
.
הגדרה
סדרה 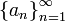 היא סדרה מתבדרת אם כל מספר ממשי a אינו הגבול של
היא סדרה מתבדרת אם כל מספר ממשי a אינו הגבול של 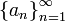 .
.
דוגמאות לסדרות מתבדרות
1) 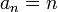
2) 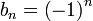
הערות
1) שתי סדרות הן שוות אם ורק אם 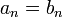 לכל n טבעי, למשל סדרה 101010... שונה מהסדרה 010101...
לכל n טבעי, למשל סדרה 101010... שונה מהסדרה 010101...
2) אם סדרה מתכנסת לגבול אזי הוא יחיד, כלומר אם N הוא גבול של סדרה וגם L הוא גבול של אותה סדרה אזי N=L.
הגדרות
1) נאמר כי סדרה 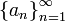 מתכנסת לאיסוף או שואפת לאיסוף אם לכל מספר ממשי M כמעט כל איברי הסדרה גדולים מ-M, ז"א לכל M קיים
מתכנסת לאיסוף או שואפת לאיסוף אם לכל מספר ממשי M כמעט כל איברי הסדרה גדולים מ-M, ז"א לכל M קיים 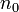 טבעי כך שלכל
טבעי כך שלכל 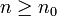
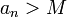 ונרשום
ונרשום 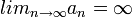 .
.
2) נאמר שסדרה 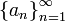 מתכנסת למינוס אינסוף אם לכל L קיים
מתכנסת למינוס אינסוף אם לכל L קיים 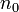 טבעי כל שלכל
טבעי כל שלכל 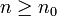
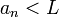 ונרשום
ונרשום 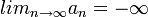
לדוגמה
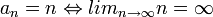
טכניקות בסיסיות לחישוב כבולות
תרגיל:
חשב כבול של 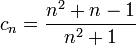
פתרון:
גם המונה וגם המכנה שואפים לאינסוף לכן לא נוכל מידית להסיק מה הוא הגבול ולכן נשתמש בטריק הבא: נבחר את החזקה הכי גבוהה של n בביטוי במקרה שלה היא 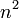 ונוציא אותה מחות לסוגריים גם במונה וגם במכנה ונקבל:
ונוציא אותה מחות לסוגריים גם במונה וגם במכנה ונקבל:
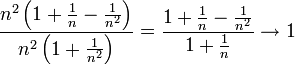 .
.
טענה (כלל המנה)
אם  אז
אז 
ואם 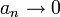 אז
אז 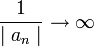
תרגיל
מצא את הגבול של 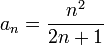
פתרון
נשתמש באותו טריק כמו בתרגיל הקודם 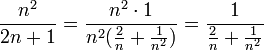
נתבונן בסדרה 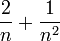 ברור שהגבול שלה הוא אפס ולכן לפי הלמה הקודמת
ברור שהגבול שלה הוא אפס ולכן לפי הלמה הקודמת 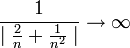 אבל כל אחד מאיברי הסדרה הוא חיובי ולכן ניתן להוריד את ערך המוחלט ונקבל
אבל כל אחד מאיברי הסדרה הוא חיובי ולכן ניתן להוריד את ערך המוחלט ונקבל 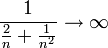 .
.
טענה:
אם 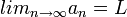 ואם לכל n
ואם לכל n 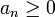 אזי
אזי 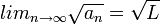 .
.
תרגיל
חשבו את 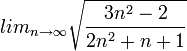
פתרון
נתבונן בסדרה 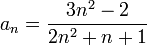 ברור שכל איברי הסדרה הם אי שליליים ולכן נוכל להשתמש בטענה הקודמת:
ברור שכל איברי הסדרה הם אי שליליים ולכן נוכל להשתמש בטענה הקודמת:
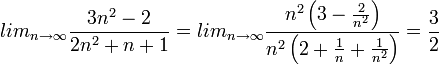 ולכן הגבול של הסדרה שלנו הוא פשוט:
ולכן הגבול של הסדרה שלנו הוא פשוט: 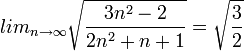
הערה
אם 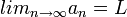 וכל איברי הסדרה הם אי שליליים אזי
וכל איברי הסדרה הם אי שליליים אזי ![lim_{n\rightarrow\infty}\sqrt[k]{a_{n}}=\sqrt[k]{L}](/images/math/f/4/b/f4bfd897e7105fc655fd9e94496553f3.png) .
.
כפל במספר צמוד
תרגיל
חשב את הגבול של 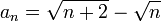
פתרון
מחובר הראשון נוסחה של האיבר הכללי שואף לאינסוף ואילו המחובר השני שואף ומינוס אינסוף ולכן לא מובן כאן מה יכול להיות הגבול, ולכן נכפיל את המונה ואת המכנה במסר צמוד ונחשב את הגבול:
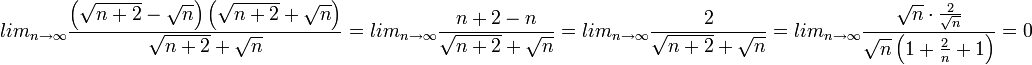
תרגיל
חשב את הגבול של 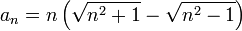
פתרון
גם כאן נכפיל ונחלק את הביטוי במספר צמוד ונקבל:
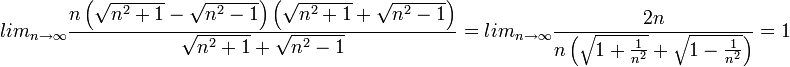
שאלה
האם סדרה חייבת להתכנס למספר או לפלוס איסוף או למינוס איסוף?
תשובה
לא!
דוגמאות לסדרות שלא מתכנסות לא למספר ולא לאינסוף ולא למינוס אינסוף
1) 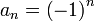
2) 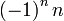
טענה
תהי 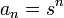 סדרה הנדסית. אזי
סדרה הנדסית. אזי 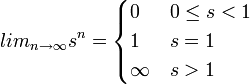
תרגיל
חשב את הגבול של 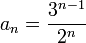
פתרון
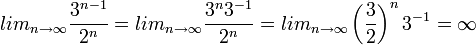
השוויון האחרון נכון כי  היא סדרה הנדסית בבסיס
היא סדרה הנדסית בבסיס 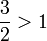 ולכן לפי טענה קודמת קיבלנו שהגבול הוא אינסופי.
ולכן לפי טענה קודמת קיבלנו שהגבול הוא אינסופי.