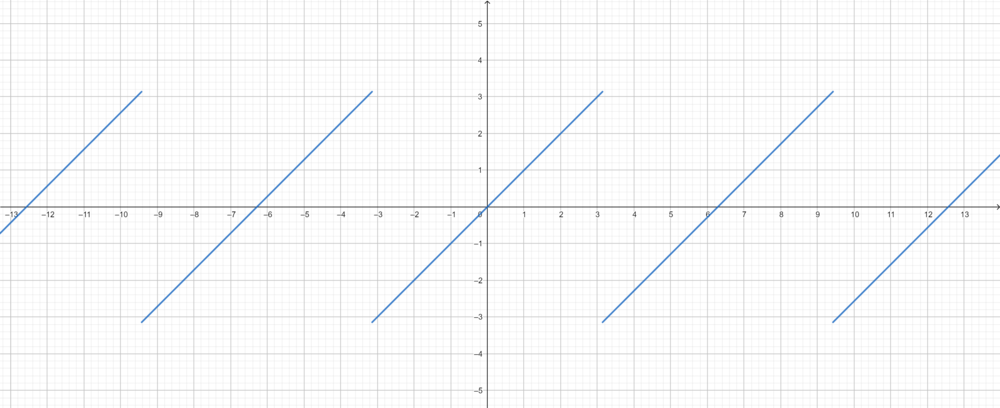אנליזת פורייה - ארז שיינר: הבדלים בין גרסאות בדף
| (181 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
[[קטגוריה:מערכי לימוד]] | |||
=מבחנים לדוגמא= | =מבחנים לדוגמא= | ||
*[[מדיה:20ForierTestA.pdf|מועד א' תש"ף]] | |||
**[[מדיה:20ForierTestASol.pdf|פתרונות סופיים למועד א' תש"ף]] | |||
*[[מדיה:20ForierTestB.pdf|מועד ב' תש"ף]] | |||
*[[מדיה:19ForierExmplTest.pdf|מבחן לדוגמא תשע"ט]] | |||
**[[מדיה:19ForierExmplTestSol.pdf|פתרון מבחן לדוגמא תשע"ט]] | |||
*[[מדיה:19ForierTestA.pdf|מועד א' תשע"ט]] | |||
**[[מדיה:19ForierTestASol.pdf|פתרון חלקי מאד מועד א' תשע"ט]] | |||
*[[מדיה:19ForierTestB.pdf|מועד ב' תשע"ט]] | |||
**[[מדיה:19ForierTestBSol.pdf|פתרון מועד ב' תשע"ט]] | |||
=תקציר ההרצאות= | =תקציר ההרצאות= | ||
*ההרצאות מבוססות בחלקן על הספר המצויין [https://samyzaf.com/technion/fourier/fourier.pdf 'טורי פוריה' של זעפרני ופינקוס]. | |||
עוד ספרים מתמטיים בסגנון ניתן למצוא [https://samyzaf.com/ באתר של סמי זערפני]. | |||
==הרצאה 1 - הקדמה ומקדמי פוריה== | |||
===הקדמה - גלים=== | |||
*מבלי להגדיר גל במפורש, גל הוא תופעה מחזורית. | *מבלי להגדיר גל במפורש, גל הוא תופעה מחזורית. | ||
*לגל שהוא פונקציה במשתנה אחד של ציר הזמן יש שלוש תכונות: | *לגל שהוא פונקציה במשתנה אחד של ציר הזמן יש שלוש תכונות: | ||
| שורה 43: | שורה 57: | ||
*במהלך ההרצאות נענה (לפחות חלקית) על השאלות הללו. | *במהלך ההרצאות נענה (לפחות חלקית) על השאלות הללו. | ||
==טורי פורייה== | |||
===טורי פורייה ומקדמי פוריה=== | |||
*טור פורייה הוא טור מהצורה <math>f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty \left[a_n\cos(nx)+b_n\sin(nx)\right]</math> | *טור פורייה הוא טור מהצורה <math>f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty \left[a_n\cos(nx)+b_n\sin(nx)\right]</math> | ||
| שורה 50: | שורה 65: | ||
===חישובים להקדמה=== | ====חישובים להקדמה==== | ||
*ראשית נזכור את הנוסחאות הטריגונומטריות: | *ראשית נזכור את הנוסחאות הטריגונומטריות: | ||
**<math>\sin(a)\sin(b)=\frac{1}{2}\left[\cos(a-b)-\cos(a+b)\right]</math> | **<math>\sin(a)\sin(b)=\frac{1}{2}\left[\cos(a-b)-\cos(a+b)\right]</math> | ||
| שורה 62: | שורה 77: | ||
**<math>\frac{1}{\pi}\int_{-\pi}^{\pi}\cos(nx)\cos(nx)dx = \frac{1}{2\pi}\int_{-\pi}^{\pi}(\cos(2nx)+1)dx = \frac{1}{2\pi}\left[\frac{1}{2n}\sin(2nx)+x\right]_{-\pi}^{\pi}=1 </math> | **<math>\frac{1}{\pi}\int_{-\pi}^{\pi}\cos(nx)\cos(nx)dx = \frac{1}{2\pi}\int_{-\pi}^{\pi}(\cos(2nx)+1)dx = \frac{1}{2\pi}\left[\frac{1}{2n}\sin(2nx)+x\right]_{-\pi}^{\pi}=1 </math> | ||
*עבור <math>n\neq k \in \mathbb{N}</math> נקבל: | *עבור <math>n\neq k \in \mathbb{N}</math> נקבל: | ||
**<math>\int_{-\pi}^{\pi}\cos(nx)\cos(kx)dx = \frac{1}{2}\int_{-\pi}^{\pi}(\cos((n+k)x)+\cos((n-k)x))dx = \frac{1}{2}\left[\frac{\sin((n | **<math>\int_{-\pi}^{\pi}\cos(nx)\cos(kx)dx = \frac{1}{2}\int_{-\pi}^{\pi}(\cos((n+k)x)+\cos((n-k)x))dx = \frac{1}{2}\left[\frac{\sin((n+k)x)}{n+k}+\frac{\sin((n-k)x)}{n-k}\right]_{-\pi}^{\pi}=0</math> | ||
**שימו לב כי השתמשנו כאן בעובדה ש<math>n-k,n+k\neq 0</math>. | **שימו לב כי השתמשנו כאן בעובדה ש<math>n-k,n+k\neq 0</math>. | ||
*עבור <math>n,k\in \mathbb{N}</math> נקבל: | *עבור <math>n,k\in \mathbb{N}</math> נקבל: | ||
| שורה 69: | שורה 84: | ||
**<math>\frac{1}{\pi}\int_{-\pi}^{\pi}\cos(0)\cos(0)dx=\frac{1}{\pi}\int_{-\pi}^{\pi}1dx=2</math> | **<math>\frac{1}{\pi}\int_{-\pi}^{\pi}\cos(0)\cos(0)dx=\frac{1}{\pi}\int_{-\pi}^{\pi}1dx=2</math> | ||
*שימו לב שכאשר מציבים 0 בsin מקבלים אפס, ולכן אין צורך בבדיקה הזו. | *שימו לב שכאשר מציבים 0 בsin מקבלים אפס, ולכן אין צורך בבדיקה הזו. | ||
*כמו כן קל לחשב <math>\int_{-\pi}^{\pi} \sin(x)dx = \int_{-\pi}^{\pi} \cos(x)dx=0</math> | |||
| שורה 74: | שורה 90: | ||
**למעשה כלל החישובים שעשינו לעיל מוכיחים שהקבוצה <math>\{\frac{1}{\sqrt{2}},sin(x),cos(x),sin(2x),cos(2x),...\}</math> מהווה קבוצה אורתונורמלית לפי המכפלה הפנימית <math>\langle f,g\rangle=\frac{1}{\pi}\int_{-\pi}^{\pi}(f\cdot g) dx</math> | **למעשה כלל החישובים שעשינו לעיל מוכיחים שהקבוצה <math>\{\frac{1}{\sqrt{2}},sin(x),cos(x),sin(2x),cos(2x),...\}</math> מהווה קבוצה אורתונורמלית לפי המכפלה הפנימית <math>\langle f,g\rangle=\frac{1}{\pi}\int_{-\pi}^{\pi}(f\cdot g) dx</math> | ||
===מקדמי הטור=== | ====מקדמי הטור==== | ||
*כעת תהי פונקציה ששווה לטור פורייה, ועוד נניח שהטור מתכנס במ"ש. | *כעת תהי פונקציה ששווה לטור פורייה, ועוד נניח שהטור מתכנס במ"ש. | ||
| שורה 101: | שורה 117: | ||
====דוגמא==== | =====דוגמא===== | ||
*נחשב את מקדמי הפורייה של ההמשך המחזורי של <math>x^2</math> | *נחשב את מקדמי הפורייה של ההמשך המחזורי של <math>x^2</math> | ||
*שימו לב, מקדמי הפורייה של פונקציה וההמשך המחזורי שלה זהים, כיוון שערך הפונקציה בנקודה אחת לא משפיע על האינטגרל. | *שימו לב, מקדמי הפורייה של פונקציה וההמשך המחזורי שלה זהים, כיוון שערך הפונקציה בנקודה אחת לא משפיע על האינטגרל. | ||
| שורה 132: | שורה 148: | ||
=== | ==הרצאה 2 - למת רימן לבג, גרעין דיריכלה== | ||
*E הוא המרחב הוקטורי של כל הפונקציות הרציפות למקוטעין <math>f:[-\pi,\pi]\to\mathbb{C}</math> מעל השדה <math>\mathbb{C}</math>. | ===מרחבי מכפלה פנימית שאינם ממימד סופי והיטלים=== | ||
** | *פונקציה נקראת רציפה למקוטעין בקטע סופי אם: | ||
**1. היא רציפה פרט אולי למספר סופי של נקודות. | |||
**2. הגבולות החד צדדיים הרלוונטיים בכל נקודה הם סופיים. | |||
*למעשה נקודות אי הרציפות היחידות של פונקציה רציפה למקוטעין הן ממין ראשון (קפיצתיות). | |||
*פונקציה נקראת רציפה למקוטעין בקטע כללי, אם ניתן לחלק אותו לקטעים סופיים בהן הפונקציה רציפה למקוטעין. | |||
*E הוא המרחב הוקטורי של כל הפונקציות הרציפות למקוטעין <math>f:[-\pi,\pi]\to\mathbb{C}</math> מעל השדה <math>\mathbb{C}</math>, המקיימות בנוסף שבכל נקודה ערך הפונקציה שווה לממוצע בין הגבולות החד צדדיים שלה, ובקצוות ערך הנקודה שווה לגבול החד צדדי המוגדר. | |||
**לא קשה להוכיח שאכן מדובר במרחב וקטורי. בעיקר יש לשים לב לכך שסכום פונקציות בקבוצה נשאר בקבוצה. | |||
*<math>\langle f,g\rangle=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\overline{g(x)}dx</math> היא מכפלה פנימית מעל E. | *<math>\langle f,g\rangle=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\overline{g(x)}dx</math> היא מכפלה פנימית מעל E. | ||
**<math>\langle g,f\rangle = \frac{1}{\pi}\int_{-\pi}^{\pi}g(x)\overline{f(x)}dx = \overline{\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\overline{g(x)}dx} = \overline{\langle f,g\rangle}</math> | |||
**<math>\langle af+bg,h\rangle = a\langle f,h\rangle + b\langle g,h\rangle </math> | |||
**<math>\langle f,f\rangle = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\overline{f(x)}dx = \frac{1}{\pi}\int_{-\pi}^{\pi}|f|^2dx</math> | |||
***בכל קטע רציפות האינטגרל על פונקציה חיובית הוא אפס אם ורק אם היא אפס. | |||
***כיוון שהפונקציה בכל נקודה שווה לאחד הגבולות החד צדדיים או לממוצע בניהם, נובע שאם האינטגרל לעיל מתאפס הפונקציה חייבת להתאפס לחלוטין. | |||
*נביט בנורמה המושרית <math>||f||^2=\langle f,f\rangle</math> | *נביט בנורמה המושרית <math>||f||^2=\langle f,f\rangle</math> | ||
*תהי קבוצה אורתונורמלית סופית <math>\{e_1,...,e_n\}</math> | *כעת נוכיח מספר תכונות של היטלים במרחבי מכפלה פנימית. | ||
*יש לנקוט בזהירות מיוחדת בנושא זה, כיוון שאנו עוסקים במרחבים שאינם נוצרים סופית (אין להם בסיס סופי או מימד). | |||
*ייתכן שהוכחתם חלק מהמשפטים הבאים רק עבור מרחבים נוצרים סופית. | |||
*תהי קבוצה אורתונורמלית סופית <math>\{e_1,...,e_n\}</math>, ונקרא למרחב שהיא פורשת W. | |||
*לכל וקטור <math>v\in V</math> נגדיר את ההיטל של <math>v</math> על W על ידי <math>\widetilde{v}=\sum_{i=1}^n\langle v,e_i\rangle e_i</math> | *לכל וקטור <math>v\in V</math> נגדיר את ההיטל של <math>v</math> על W על ידי <math>\widetilde{v}=\sum_{i=1}^n\langle v,e_i\rangle e_i</math> | ||
*מתקיים כי <math>\langle v,\widetilde{v}\rangle = \langle \widetilde{v},\widetilde{v}\rangle</math> | *נוכיח מספר תכונות לגבי ההיטל הזה: | ||
**הוכחה | |||
* | |||
** | *מתקיים כי <math>\langle v,\widetilde{v}\rangle = \langle \widetilde{v},\widetilde{v}\rangle=\sum_{i=1}^n |\langle v,e_i\rangle|^2</math> | ||
**הוכחה: | |||
**<math>\langle v,\widetilde{v}\rangle = \langle v,\sum_{i=1}^n\langle v,e_i\rangle e_i\rangle = \sum_{i=1}^n \overline{\langle v,e_i\rangle}\langle v,e_i\rangle = \sum_{i=1}^n |\langle v,e_i\rangle|^2</math> | |||
**<math>\langle \widetilde{v},\widetilde{v}\rangle = \langle \sum_{i=1}^n\langle v,e_i\rangle e_i,\sum_{i=1}^n\langle v,e_i\rangle e_i\rangle = \sum_{i=1}^n |\langle v,e_i\rangle|^2</math> | |||
**המעבר האחרון נכון כיוון ש <math>\{e_1,...,e_n\}</math> אורתונורמלית. | |||
*מתקיים כי <math>||v||^2=||v-\widetilde{v}||^2+||\widetilde{v}||^2</math> | *מתקיים כי <math>||v||^2=||v-\widetilde{v}||^2+||\widetilde{v}||^2</math> | ||
**הוכחה | **הוכחה: | ||
*מסקנה | **<math>\langle v-\widetilde{v},v-\widetilde{v}\rangle = \langle v,v\rangle - \langle v,\widetilde{v}\rangle - \langle \widetilde{v},v\rangle + \langle \widetilde{v},\widetilde{v}\rangle</math> | ||
**נזכור כי <math>\langle v,\widetilde{v}\rangle = \langle \widetilde{v},\widetilde{v}\rangle</math>. | |||
**לכן קיבלנו כי <math>||v-\widetilde{v}||^2 = ||v||^2 - ||\widetilde{v}||^2</math> | |||
*מסקנה מיידית: <math>||\widetilde{v}||\leq ||v||</math> | |||
====אי שיוויון בסל==== | |||
*כעת תהי קבוצה אורתונורמלית אינסופית <math>\{e_1,e_2,...\}</math>. | |||
*לכל <math>v\in V</math> מתקיים כי <math>\sum_{i=1}^\infty |\langle v,e_i\rangle|^2 \leq ||v||^2</math> | |||
**הוכחה: | |||
**ראינו שלכל n מתקיים כי <math>\sum_{i=1}^n |\langle v,e_i\rangle|^2 \leq ||v||^2</math>. | |||
**כלומר סדרת הסכומים החלקיים של הטור החיובי חסומה על ידי <math>||v||^2</math> ולכן הטור מתכנס למספר שקטן או שווה לו. | |||
*בפרט נובע כי | |||
:<math>\lim_{n\to\infty}|\langle v,e_i\rangle|=0</math> | |||
===למת רימן לבג=== | ===למת רימן לבג=== | ||
*ראינו כי <math>\{\sin(x),\cos(x),\sin(2x),\cos(2x),...\}</math> היא קבוצה אורתונורמלית ב<math>E</math> (כרגע אנו לא צריכים את הפונקציה הקבועה). | |||
*כמו כן לכל פונקציה f הגדרנו מקדמי פורייה ע"י: | |||
*לכל <math>1\leq n\in \mathbb{N}</math> הגדרנו <math>a_n=\langle f,\cos(nx)\rangle</math>, ו<math>b_n=\langle f,\sin(nx)\rangle</math> | |||
*נובע מאי שיוויון בסל כי המקדמים שואפים לאפס. | |||
*כלומר: | |||
:<math>\lim_{n\to\infty}\frac{1}{\pi}\int_{-\pi}^\pi f(x)\cos(nx)dx = 0</math> | |||
:<math>\lim_{n\to\infty}\frac{1}{\pi}\int_{-\pi}^\pi f(x)\sin(nx)dx = 0</math> | |||
*למת רימן-לבג: תהי <math>g</math> רציפה למקוטעין בקטע <math>[0,\pi]</math>, אזי: | |||
:<math>\lim_{n\to\infty}\int_{0}^\pi g(t)\sin\left(\left(n+\frac{1}{2}\right)t\right)dt = 0</math> | |||
*הוכחה: | |||
**<math>\int_{0}^\pi g(t)\sin\left(\left(n+\frac{1}{2}\right)t\right)dt = \int_{0}^\pi g(t)\cos(\frac{t}{2})\sin(nt) dt+\int_{0}^\pi g(t)\sin(\frac{t}{2})\cos(nt) dt | |||
</math> | |||
**נגדיר את שתי הפונקציות <math>h_s(t)=\begin{cases}g(t)\sin(\frac{t}{2}) & 0\leq t\leq \pi \\ 0 & -\pi\leq t <0\end{cases}</math> ו <math>h_c(t)=\begin{cases}g(t)\cos(\frac{t}{2}) & 0\leq t\leq \pi \\ 0 & -\pi\leq t <0\end{cases}</math> | |||
**קל לראות כי שתי הפונקציות רציפות למקוטעין. לכן פרט לשינוי במספר סופי של נקודות שלא משפיע על האינטגרל, ניתן להניח כי <math>h_c,h_s\in E</math>. | |||
**ביחד נקבל כי <math>\int_{0}^\pi g(t)\sin\left(\left(n+\frac{1}{2}\right)t\right)dt = \int_{-\pi}^\pi h_c(t)\sin(nt)dt + \int_{-\pi}^\pi h_s(t)\cos(nt)dt \to 0</math> | |||
===גרעין דיריכלה=== | |||
*גרעין דיריכלה הוא הפונקציה <math>D_n(t)= \frac{\sin\left(\left(n+\frac{1}{2}\right)t\right)}{2\sin(\frac{t}{2})}</math> | |||
*טענה: <math>D_n(t)=\frac{1}{2}+\sum_{k=1}^n \cos(kt)</math> בכל נקודה <math>t\neq 2\pi k</math> | |||
**הוכחה: | |||
**נכפל ב<math>2\sin(\frac{t}{2})</math> ונקבל בצד שמאל: | |||
**<math>\sin(\frac{t}{2}) + 2\sin(\frac{t}{2})\cos(t) + 2\sin(\frac{t}{2})\cos(2t)+...+2\sin(\frac{t}{2})\cos(nt)</math> | |||
**נבחין בזהות הטריגונומטרית <math>2\sin(a)\cos(b) = \sin(b+a)-\sin(b-a)</math> | |||
**ובפרט <math>2\sin(\frac{t}{2})\cos(kt) = \sin(kt+\frac{t}{2}) - \sin(kt-\frac{t}{2})</math> | |||
**ביחד נקבל <math>\sin(\frac{t}{2}) + \sin(t+\frac{t}{2})-\sin(t-\frac{t}{2}) + \sin(2t+\frac{t}{2}) - \sin(2t-\frac{t}{2})+...+\sin(nt+\frac{t}{2}) - \sin(nt-\frac{t}{2}) = \sin(nt+\frac{t}{2}) = \sin\left(\left(n+\frac{1}{2}\right)t\right)</math> | |||
*נשים לב כי הפונקציה <math>2\sin(\frac{t}{2})</math> מתאפסת בנקודות <math>t=2\pi k</math>, בנקודות אלו לגרעין דיריכלה יש אי רציפות סליקה. | |||
*זה נכון כיוון שפרט לנקודות אלו מדובר בפונקציה רציפה. | |||
*כמו כן, גרעין דיריכלה מחזורי <math>2\pi</math> כיוון שהוא סכום של פונקציות מחזוריות <math>2\pi</math>. | |||
*נחשב את האינטגרל על גרעין דיריכלה: | |||
*ראשית, לכל <math>1\leq k \in \mathbb{N}</math> מתקיים: | |||
:<math>\int_0^\pi \cos(kt)dt = \left[\frac{\sin(kt)}{k}\right]_0^\pi = 0</math> | |||
*לכן נקבל: | |||
:<math>\frac{1}{\pi}\int_0^\pi D_n(t)dt = \frac{1}{\pi}\int_0^\pi \left[\frac{1}{2} + \cos(t) + \cos(2t)+...+\cos(nt)\right]dt = \frac{1}{\pi}\int_0^\pi \frac{1}{2}dt = \frac{1}{2}</math> | |||
====הסכומים החלקיים של טור פוריה==== | |||
*תהיה נקודה x, נביט בסדרת הסכומים החלקיים של טור הפוריה המתאים לפונקציה <math>f</math> שהיא מחזורית <math>2\pi</math>: | |||
:<math>S_n = \frac{a_0}{2} + \sum_{k=1}^n a_k\cos(kx)+b_k\sin(kx)</math> | |||
*נציב את מקדמי פוריה ונקבל כי: | |||
:<math>S_n = \frac{1}{\pi}\int_{-\pi}^\pi \frac{1}{2}f(t)dt + \sum_{k=1}^n \left[\frac{1}{\pi}\int_{-\pi}^\pi f(t)\cos(kt)dt\right]\cos(kx)+\left[\frac{1}{\pi}\int_{-\pi}^\pi f(t)\sin(kt)dt\right]\sin(kx)=</math> | |||
:<math>= \frac{1}{\pi}\int_{-\pi}^\pi\left[\frac{1}{2}f(t)+\sum_{k=1}^n f(t)\left(\cos(kt)\cos(kx) + \sin(kt)\sin(kx)\right)\right]dt=</math> | |||
:<math>=\frac{1}{\pi}\int_{-\pi}^\pi f(t)\left[\frac{1}{2}+\sum_{k=1}^n \cos(k(t-x))\right]dt</math> | |||
*זה בעצם גרעין דיריכלה, כלומר קיבלנו כי: | |||
:<math>S_n = \frac{1}{\pi}\int_{-\pi}^\pi f(t)D_n(t-x)dt</math> | |||
*שימו לב ששינוי מספר סופי של נקודות לא משפיע על האינטגרל, ולכן נקודות אי הרציפות הסליקות של גרעין דיריכלה לא פוגעות בהוכחה. | |||
*טענה: תהי <math>f</math> פונקציה מחזורית <math>2\pi</math>. אזי לכל <math>a\in\mathbb{R}</math> מתקיים כי: | |||
:<math>\int_{-\pi}^\pi f(x)dx = \int_{-\pi+a}^{\pi+a} f(x)dx</math> | |||
*כלומר, השטח מתחת לגרף הפונקציה שווה על כל קטע באורך <math>2\pi</math>. | |||
**הוכחה: | |||
::<math>\int_{-\pi+a}^{\pi+a} f(x)dx = \int_{-\pi+a}^{\pi} f(x)dx + \int_{\pi}^{\pi+a} f(x)dx</math> | |||
::נבצע הצבה <math>t=x-2\pi</math> באינטגרל השני ונקבל: | |||
::<math>\int_{\pi}^{\pi+a} f(x)dx = \{t=x-2\pi, dt=dx\} = \int_{-\pi}^{-\pi+a}f(t+2\pi)dt = \int_{-\pi}^{-\pi+a}f(t)dt = \int_{-\pi}^{-\pi+a}f(x)dx</math> | |||
::ביחד נקבל כי: | |||
::<math>\int_{-\pi+a}^{\pi+a} f(x)dx=\int_{-\pi+a}^{\pi} f(x)dx + \int_{-\pi}^{-\pi+a}f(x)dx = \int_{-\pi}^\pi f(x)dx</math> | |||
*נחזור לסכומים החלקיים ונבצע הצבה: | |||
:<math>S_n = \frac{1}{\pi}\int_{-\pi}^\pi f(t)D_n(t-x)dt = \{ u=t-x, du=dt\} = \frac{1}{\pi}\int_{-\pi-x}^{\pi-x} f(x+u)D_n(u)du</math> | |||
:כיוון שגרעין דיריכלה ו<math>f</math> הן מחזוריות, נקבל: | |||
:<math>S_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x+u)D_n(u)du=\frac{1}{\pi}\int_{-\pi}^{\pi} f(x+t)D_n(t)dt</math> | |||
==הרצאה 3 התכנסות נקודתית של טורי פוריה== | |||
===סימונים והגדרות=== | |||
*נסמן את הגבול החד צדדי מימין ב<math>f(d^+)=\lim_{x\to d^+}f(x)</math>. | |||
*נסמן את הגבול החד צדדי משמאל ב<math>f(d^-)=\lim_{x\to d^-}f(x)</math>. | |||
*שימו לב: אם הפונקציה רציפה למקוטעין, הערכים הללו תמיד מוגדרים. | |||
*נגדיר את הנגזרת הימנית ע"י <math>f'(x^+) = \lim_{t\to 0^+}\frac{f(x+t)-f(x^+)}{t}</math>. | |||
*נגדיר את הנגזרת השמאלית ע"י <math>f'(x^-) = \lim_{t\to 0^-}\frac{f(x+t)-f(x^-)}{t}</math>. | |||
*שימו לב: ייתכן ש<math>f'(d^+)=f'(d^-)</math> אך הפונקציה אינה גזירה בd. זה יקרה אם היא לא רציפה בנקודה. | |||
דוגמא: | |||
*נביט בפונקציה <math>f(x)=\frac{x}{|x|}</math> | |||
*מתקיים כי <math>f(0^+)=1</math>, ו<math>f(0^-)=-1</math>. | |||
*כמו כן מתקיים כי <math>f'(0^+)=f'(0^-)=0</math>. | |||
כמובן שהפונקציה אינה רציפה ואינה גזירה ב0. | |||
===משפט דיריכלה - התכנסות נקודתית של טור פוריה=== | |||
*תהי <math>f</math> פונקציה מחזורית <math>2\pi</math>, רציפה למקוטעין כך שבכל נקודה הנגזרות החד צדדיות שלה קיימות וסופיות. | |||
*אזי לכל <math>x\in\mathbb{R}</math> הטור עם מקדמי הפוריה של <math>f</math> מתכנס: | |||
:<math>\frac{f(x^+)+f(x^-)}{2}=\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx) + b_n\sin(nx)</math> | |||
*בפרט, בכל נקודה בה הפונקציה רציפה טור הפוריה מתכנס נקודתית לפונקציה, ובכל נקודה בה יש אי רציפות קפיצתית טור הפוריה מתכנס לממוצע הגבולות מימין ומשמאל. | |||
====הוכחה==== | |||
*תהי נקודה <math>x\in\mathbb{R}</math>. | |||
*נביט בפונקציה <math>g(t) = \frac{f(x+t) - f(x^+)}{2\sin(\frac{t}{2})}</math> | |||
*<math>\lim_{t\to 0^+}g(t) = \lim_{t\to 0^+}\frac{f(x+t) - f(x^+)}{t}\frac{\frac{t}{2}}{\sin(\frac{t}{2})} = f'(x^+)\cdot 1</math> | |||
*כיוון שהנגזרות החד צדדיות קיימות וסופיות, קיבלנו ש<math>g(t)</math> רציפה למקוטעין בקטע <math>[0,\pi]</math>. | |||
*לפי למת רימן-לבג נובע כי: | |||
:<math>\lim_{n\to\infty}\int_0^\pi g(t)\sin\left(\left(n+\frac{1}{2}\right)t\right)dt=0</math> | |||
*כלומר: | |||
:<math>0=\lim_{n\to\infty}\frac{1}{\pi}\int_0^\pi \left[f(x+t)-f(x^+)\right]\frac{\sin\left(\left(n+\frac{1}{2}\right)t\right)}{2\sin(\frac{t}{2})}dt= | |||
\lim_{n\to\infty}\frac{1}{\pi}\int_0^\pi \left[f(x+t)-f(x^+)\right]D_n(t)dt</math> | |||
*כיוון ש | |||
:<math>\frac{1}{\pi}\int_0^\pi f(x^+)D_n(t)dt = \frac{f(x^+)}{2}</math> | |||
*נובע כי: | |||
:<math>\lim_{n\to\infty}\frac{1}{\pi}\int_0^\pi f(x+t)D_n(t)dt = \frac{f(x^+)}{2}</math> | |||
*באופן דומה לחלוטין ניתן להוכיח כי: | |||
:<math>\lim_{n\to\infty}\frac{1}{\pi}\int_{-\pi}^0 f(x+t)D_n(t)dt = \frac{f(x^-)}{2}</math> | |||
*ולכן סה"כ נקבל כי: | |||
:<math>\lim_{n\to\infty} S_n(x)= \lim_{n\to\infty}\frac{1}{\pi}\int_{-\pi}^{\pi} f(x+t)D_n(t)dt = \frac{f(x^-)+f(x^+)}{2}</math> | |||
====דוגמאות==== | |||
=====דוגמא 1===== | |||
*תהי <math>f</math> ההמשך המחזורי של <math>x</math>. | |||
:[[קובץ:x_fourier.png|1000px]] | |||
*כיוון שf רציפה למקוטעין ובעלת נגזרות חד צדדיות קיימות (כולן שוות 1), תנאי משפט דיריכלה מתקיימים. | |||
*כיוון שf הינה אי-זוגית, לכל <math>n</math> מתקיים כי <math>a_n=0</math>. | |||
*כעת נחשב את המקדמים של הסינוסים: | |||
:<math>b_n=\langle f,sin(nx)\rangle = \frac{1}{\pi}\int_{-\pi}^\pi x\sin(nx)dx =\frac{2}{\pi}\int_{0}^\pi x\sin(nx)dx= \frac{2}{n\pi}\left[-x\cos(nx)\right]_{0}^\pi + \frac{2}{n\pi}\int_{0}^{\pi}\cos(nx)dx = | |||
-\frac{2\pi\cos(\pi n)}{\pi n} = \frac{2(-1)^{n+1}}{n}</math> | |||
*לכן, בכל נקודת רציפות של f, כלומר בכל נקודה <math>x\neq \pi +2\pi k</math>, מתקיים כי: | |||
:<math>f(x)=\sum_{n=1}^\infty\frac{2(-1)^{n+1}}{n}\sin(nx) </math>. | |||
*בפרט, לכל נקודה <math>x\in (-\pi,\pi)</math> מתקיים כי: | |||
:<math>x=\sum_{n=1}^\infty\frac{2(-1)^{n+1}}{n}\sin(nx)</math> | |||
*עבור נקודות אי הרציפות (הקפיצתיות), מתקיים כי הממוצע בין הגבולות החד צדדיים הוא אפס. | |||
*קל לראות שאכן לכל <math>x=\pi+2\pi k</math> נקבל שטור הפורייה מתכנס לאפס (למעשה כל הסינוסים מתאפסים). | |||
*נציב לדוגמא <math>x=\frac{\pi}{2}</math> ונקבל: | |||
:<math>\frac{\pi}{2}=\sum_{n=1}^\infty\frac{2(-1)^{n+1}}{n}\sin(\frac{n\pi}{2}) </math> | |||
*לכל n זוגי הסינוס יתאפס, ולכן נקבל: | |||
:<math>\frac{\pi}{2}=\sum_{n=1}^\infty\frac{2}{2n-1}\sin(n\pi-\frac{\pi}{2}) =\sum_{n=1}^\infty\frac{-2}{2n-1}\cos(n\pi) = \sum_{n=1}^\infty\frac{2(-1)^{n+1}}{2n-1} </math> | |||
*שימו לב שהפעם לא קיבלנו טור חדש בזכות פורייה, כיוון שנקבל בדיוק את אותו הטור אם נציב 1 בטור הטיילור של <math>arctan(x)</math>. | |||
=====דוגמא 2===== | |||
*כעת, תהי <math>g</math> ההמשך המחזורי של <math>x^2</math>. | |||
*הפונקציה g הינה רציפה בכל הממשיים. | |||
*הפונקציה g גזירה בכל הממשיים פרט לנקודות <math>x=\pi+2\pi k</math>. | |||
*בנקודות אי הגזירות, הנגזרות החד צדדיות קיימות ושוות ל<math>\pm 2\pi</math> (כיוון שהנגזרת של <math>x^2</math> היא <math>2x</math>). | |||
*סה"כ לפי משפט דיריכלה, טור הפוריה של g מתכנס אליה בכל הממשיים (כיוון שהיא רציפה בכל הממשיים). | |||
*כלומר קיבלנו שלכל <math>x\in [-\pi,\pi]</math> מתקיים כי: | |||
::<math>x^2=\frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4(-1)^n}{n^2}cos(nx)</math> | |||
*שימו לב שאם נגזור איבר איבר את טור הפוריה של <math>x^2</math>, נקבל את טור הפורייה של <math>2x</math>. | |||
*האם זה מפתיע? | |||
=====דוגמא 3===== | |||
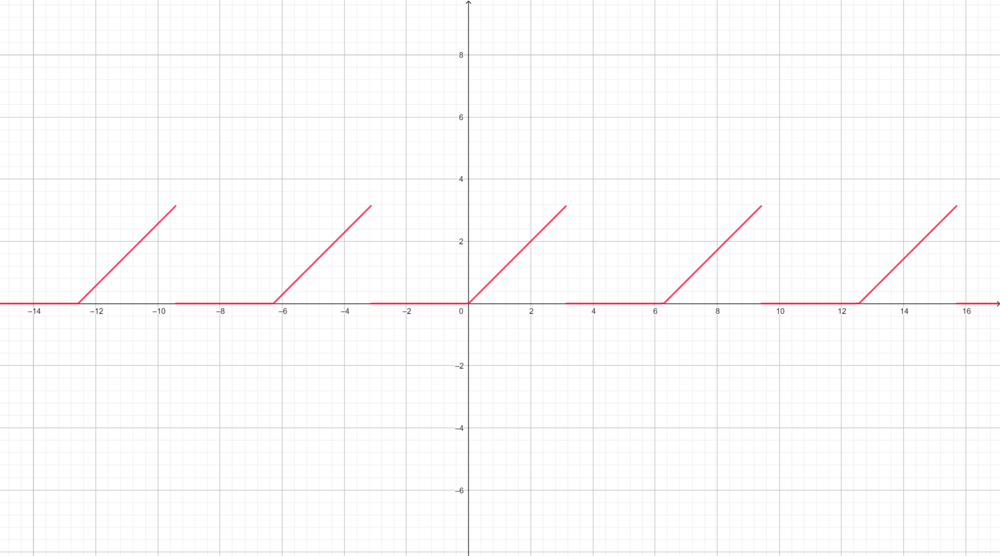
*תהי <math>h</math> ההמשך המחזורי של הפונקציה <math>\begin{cases}x & x\in [0,\pi]\\0 & x\in [-\pi,0)\end{cases}</math> | |||
:[[קובץ:x_and_0_fourier.png|1000px]] | |||
*שוב, קיבלנו פונקציה רציפה למקוטעין עם נגזרות חד צדדיות קיימות וסופיות. | |||
*נחשב את מקדמי הפורייה: | |||
:<math>a_0=\frac{1}{\pi}\int_0^\pi xdx = \frac{\pi}{2}</math> | |||
:<math>a_n = \frac{1}{\pi}\int_0^\pi x\cos(nx)dx = \frac{1}{n\pi}\left[x\sin(nx)\right]_0^\pi - \frac{1}{n\pi}\int_0^\pi \sin(nx)dx = \frac{1}{n^2\pi}\left[\cos(nx)\right]_0^\pi= | |||
\frac{(-1)^n-1}{\pi n^2}</math> | |||
:<math>b_n = \frac{1}{\pi}\int_0^\pi x\sin(nx)dx = \frac{-1}{n\pi}\left[x\cos(nx)\right]_0^\pi + \frac{1}{n\pi}\int_0^\pi \cos(nx)dx = \frac{(-1)^{n+1}}{n}</math> | |||
*סה"כ שלכל <math>x\in (-\pi,\pi)</math> מתקיים כי: | |||
:<math>h(x) = \frac{\pi}{4} + \sum_{n=1}^\infty \left[\frac{(-1)^n-1}{\pi n^2}\cos(nx) + \frac{(-1)^{n+1}}{n}\sin(nx)\right]</math> | |||
*שימו לב: מצאנו שני טורי פורייה שמתכנסים ל<math>x</math> בקטע <math>(0,\pi)</math>. | |||
*באופן דומה אפשר להראות שקיימים אינסוף טורי פורייה כאלה. | |||
===טור הנגזרת=== | |||
*תהי <math>f</math> רציפה בקטע <math>[-\pi,\pi]</math> כך שהנגזרת שלה <math>f'</math> רציפה למקוטעין בקטע. | |||
====שימוש בנוסחאת ניוטון לייבניץ לחישוב האינטגרל המסויים==== | |||
*שימו לב שמותר לנו להשתמש בנוסחאת ניוטון לייבניץ: | |||
**כיוון שהנגזרת רציפה למקוטעין, אפשר להראות בעזרת לופיטל שהנגזרות החד צדדיות בנקודות אי הגזירות של f קיימות. | |||
**בעצם, זה מראה שf גזירה בקטעים סגורים בהם אפשר להפעיל את נוסחאת ניוטון לייבניץ. | |||
**אם נחשב את האינטגרל על הנגזרת בכל הקטעים הסגורים, ערכי f יצטמצמו, פרט לקצוות. | |||
***לדוגמא: | |||
***<math>\int_{-1}^1 \frac{x}{|x|}dx = \int_{-1}^0 (-1)dx + \int_{0}^1 (1)dx = (-x)|_{-1}^0+(x)|_0^1 = 0-1 + 1-0 = 1-1</math> | |||
***כלומר קיבלנו כי <math>\int_{-1}^1 \frac{x}{|x|}dx = (|x|)_{-1}^{1}</math>, כאשר <math>(|x|)' = \frac{x}{|x|}</math> | |||
====חישוב מקדמי טור הפורייה של הנגזרת==== | |||
*נסמן את מקדמי הפורייה של <math>f</math> ב<math>a_n,b_n</math> | |||
*נחשב את מקדמי הפורייה של הנגזרת, נסמן אותם ב<math>\alpha_n,\beta_n</math>: | |||
:<math>\alpha_0=\frac{1}{\pi}\int_{-\pi}^{\pi}f'(x)dx= \frac{f(\pi)-f(-\pi)}{\pi}</math> | |||
:<math>\alpha_n=\frac{1}{\pi} \int_{-\pi}^\pi f'(x)\cos(nx)dx = \frac{1}{\pi}\left[f(x)\cos(nx)\right]_{-\pi}^\pi +\frac{n}{\pi}\int_{-\pi}^\pi f(x)\sin(nx)dx = | |||
\frac{(-1)^n\left(f(\pi)-f(-\pi)\right)}{\pi}+n\cdot b_n = (-1)^n\alpha_0+nb_n</math> | |||
:<math>\beta_n=\frac{1}{\pi} \int_{-\pi}^\pi f'(x)\sin(nx)dx = \frac{1}{\pi}\left[f(x)\sin(nx)\right]_{-\pi}^\pi -\frac{n}{\pi}\int_{-\pi}^\pi f(x)\cos(nx)dx = -n\cdot a_n</math> | |||
*כלומר, בתנאים הנתונים, אם טור הפוריה של f הינו: | |||
:<math>f(x)\sim\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx)</math> | |||
*אזי טור הפורייה של הנגזרת הינו: | |||
:<math>f'(x)\sim\frac{\alpha_0}{2}+\sum_{n=1}^\infty \left((-1)^n\alpha_0+nb_n\right)\cos(nx)-n\cdot a_n\sin(nx)</math> | |||
*במקרה המיוחד בו <math>f(-\pi)=f(\pi)</math> מתקיים כי <math>\alpha_0=0</math> ולכן נקבל את טור הפורייה הפשוט: | |||
:<math>f'(x)\sim\sum_{n=1}^\infty nb_n\cos(nx)-na_n\sin(nx)</math> | |||
====דוגמאות==== | |||
=====דוגמא 1===== | |||
*נזכר בטור הפורייה של <math>x^2</math>: | |||
:<math>\frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4(-1)^n}{n^2}cos(nx)</math> | |||
*נרצה למצוא את מקדמי הפוריה של <math>\frac{x^3}{3}</math>, נסמנם ב<math>a_n,b_n</math>. | |||
*לכל <math>1\leq n</math> נקבל כי: | |||
:<math>\frac{2(-1)^n\pi^2}{3}+nb_n = \frac{4(-1)^n}{n^2}</math> | |||
:<math>-na_n = 0</math> | |||
*כמו כן נחשב את המקדם הראשון: | |||
:<math>a_0=\frac{1}{\pi}\int_{-\pi}^\pi \frac{x^3}{3}dx = 0</math> | |||
*נחלץ את המקדמים ונקבל כי טור הפורייה של <math>\frac{x^3}{3}</math> הוא: | |||
:<math>\frac{x^3}{3} \sim \sum_{n=1}^\infty \frac{2(-1)^n}{n^3}\left(2-\frac{\pi^2 n^2}{3}\right)\sin(nx)</math> | |||
=====דוגמא 2===== | |||
*נחשב את טור הפורייה של <math>e^x</math>. | |||
*נסמן את טור הפורייה של <math>e^x</math> ב: | |||
:<math>\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx)</math> | |||
*כמובן שהנגזרת במקרה הזה שווה לפונקציה, ולכן יש לה בדיוק אותו טור פורייה. | |||
*מצד שני, טור הפורייה של הנגזרת צריך להיות: | |||
:<math>\frac{\alpha_0}{2}+\sum_{n=1}^\infty \left((-1)^n\alpha_0+nb_n\right)\cos(nx) -na_n\sin(nx)</math> | |||
*כאשר <math>\alpha_0=\frac{f(\pi)-f(-\pi)}{\pi}=\frac{e^\pi-e^{-\pi}}{\pi}</math> | |||
*ביחד נקבל את המשוואות: | |||
:<math>a_0=\alpha_0</math> | |||
:<math>a_n=(-1)^n\alpha_0+nb_n</math> | |||
:<math>b_n=-na_n</math> | |||
*נציב את המשוואה השלישית בשנייה ונקבל: | |||
:<math>a_n=\frac{(-1)^n\alpha_0}{1+n^2}</math> | |||
*ולכן | |||
:<math>b_n=\frac{n(-1)^{n+1}\alpha_0}{1+n^2}</math> | |||
*סה"כ קיבלנו כי טור הפורייה של <math>e^x</math> הינו: | |||
:<math>\frac{\alpha_0}{2}+\sum_{n=1}^\infty \frac{(-1)^n\alpha_0}{1+n^2}\cos(nx) + \frac{n(-1)^{n+1}\alpha_0}{1+n^2}\sin(nx)</math> | |||
*כיוון שלהמשך המחזורי של <math>e^x</math> יש אי רציפות קפיצתית ב<math>x=\pi</math>, טור הפורייה שם מתכנס לממוצע <math>\frac{e^\pi+e^{-\pi}}{2}</math> | |||
*כלומר, אם נציב <math>x=\pi</math> נקבל: | |||
:<math>\frac{1}{\alpha_0}\frac{e^\pi+e^{-\pi}}{2} = \frac{1}{2} +\sum_{n=1}^\infty \frac{1}{1+n^2}</math> | |||
*נפשט: | |||
:<math>\sum_{n=1}^\infty \frac{1}{1+n^2}=\frac{\pi(e^\pi+e^{-\pi})}{2(e^\pi-e^{-\pi})}-\frac{1}{2}</math> | |||
==הרצאה 4 - התכנסות במ"ש ושיוויון פרסבל== | |||
===תנאי להתכנסות במ"ש של טור פורייה=== | |||
*תהי <math>f</math> רציפה בקטע <math>[-\pi,\pi]</math> המקיימת <math>f(-\pi)=f(\pi)</math>, כך ש <math>f'</math> רציפה למקוטעין. | |||
*אזי טור הפורייה של <math>f</math> מתכנס אליה במ"ש בכל הממשיים. | |||
*לפי משפט דיריכלה ידוע כי טור הפורייה של ההמשך המחזורי של f מתכנס אליה בכל נקודה. | |||
*נסמן את טור הפורייה ב | |||
:<math>\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx)</math> | |||
*ברור כי | |||
:<math>\left|\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx)\right|\leq \frac{|a_0|}{2} + \sum_{n=1}^\infty |a_n|+|b_n|</math> | |||
*לפי מבחן ה-M של ויירשטראס, מספיק להוכיח שטור המספרים מימין מתכנס על מנת להסיק שטור הפורייה מתכנס במ"ש. | |||
*נסמן את מקדמי פורייה של הנגזרת ב<math>\alpha_n,\beta_n</math>. | |||
*כבר חישבנו ש: | |||
**<math>\alpha_0=0</math> | |||
**<math>\alpha_n=nb_n</math> | |||
**<math>\beta_n=-na_n</math> | |||
*לכן ביחד נקבל כי <math>\sqrt{|a_n|^2+|b_n|^2}=\frac{1}{n}\sqrt{|\alpha_n|^2+|\beta_n|^2}</math> | |||
*לפי אי שיוויון קושי שוורץ, נקבל כי לכל n מתקיים: | |||
:<math>\sum_{n=1}^N \frac{\sqrt{|\alpha_n|^2+|\beta_n|^2}}{n} \leq \sqrt{\sum_{n=1}^N\frac{1}{n^2}}\sqrt{\sum_{n=1}^N |\alpha_n|^2+|\beta_n|^2}</math> | |||
*לפי אי שיוויון בסל, אנו יודעים כי הטור <math>\sum_{n=1}^\infty |\alpha_n|^2+|\beta_n|^2</math> מתכנס, כיוון שמדובר במקדמי פורייה של <math>f'\in E</math>. | |||
**(זכרו שמותר להניח כי <math>f'\in E</math> על ידי שינוי מספר סופי של נקודות שלא משפיעות על חישוב מקדמי הפורייה.) | |||
*לכן <math>\left(\sum_{n=1}^N\frac{1}{n^2}\right),\left(\sum_{n=1}^N |\alpha_n|^2+|\beta_n|^2\right)</math> חסומות כסדרות סכומים חלקיים של טורים מתכנסים. | |||
*לכן סה"כ <math>\sum_{n=1}^N \frac{\sqrt{|\alpha_n|^2+|\beta_n|^2}}{n}</math> חסומה, ולכן הטור האינסופי המתאים לה מתכנס. | |||
*סה"כ קיבלנו כי <math>\sum_{n=1}^\infty \sqrt{|a_n|^2+|b_n|^2}</math> מתכנס. | |||
*לכן בוודאי גם הטורים הקטנים יותר <math>\sum_{n=1}^\infty |a_n|</math> ו<math>\sum_{n=1}^\infty |b_n|</math> מתכנסים, כפי שרצינו. | |||
===שיוויון פרסבל=== | |||
*נביט במערכת האורתונורמלית <math>\{\frac{1}{\sqrt{2}},\cos(x),\sin(x),\cos(2x),\sin(2x),...\}\subseteq E</math>, ותהי <math>f\in E</math>. | |||
*ידוע לנו כי <math>a_0=\langle f,1\rangle</math>, ולכן <math>\frac{a_0}{\sqrt{2}}=\langle f,\frac{1}{\sqrt{2}}\rangle</math> | |||
*נסמן את סדרת הסכומים החלקיים של טור הפורייה המתאים לפונקציה f ב <math>S_n</math>. | |||
*<math>S_n</math> היא ההיטל של <math>f</math> על הקבוצה האורתונורמלית <math>\{\frac{1}{\sqrt{2}},\cos(x),\sin(x),\cos(2x),\sin(2x),...,\cos(nx),\sin(nx)\}</math> | |||
**אכן <math>\langle f,\frac{1}{\sqrt{2}}\rangle \frac{1}{\sqrt{2}} + \sum_{n=1}^\infty \langle f,\cos(nx)\rangle \cos(nx) + \langle f,\sin(nx)\rangle \sin(nx) = \frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx)</math> | |||
*נזכור כי <math>||v||^2=||v-\widetilde{v}||^2+||\widetilde{v}||^2</math> | |||
**לכן <math>||f-S_n||^2=||f||^2-||S_n||^2</math>. | |||
*כמו כן, נזכור כי <math>||\widetilde{v}||^2 = \sum_{i=1}^{n}|\langle v,e_i\rangle|^2</math> | |||
**לכן <math>||S_n||^2 = \frac{|a_0|^2}{2}+\sum_{k=1}^n |a_k|^2+|b_k|^2</math> | |||
*אי שיוויון בסל אומר כי <math>\sum_{i=1}^\infty |\langle v,e_i\rangle|^2 \leq ||v||^2</math> | |||
*כלומר: | |||
:<math>\frac{|a_0|^2}{2}+\sum_{n=1}^\infty |a_n|^2+|b_n|^2 \leq ||f||^2 = \langle f,f\rangle = \frac{1}{\pi}\int_{-\pi}^{\pi} |f(x)|^2dx</math> | |||
*משפט שיוויון פרסבל אומר שבעצם מתקיים שיוויון: | |||
:<math>\frac{1}{\pi}\int_{-\pi}^{\pi} |f(x)|^2dx=\frac{|a_0|^2}{2}+\sum_{n=1}^\infty |a_n|^2+|b_n|^2 </math> | |||
*אם נוכיח ש <math>||f-S_n||^2\to 0</math>, נסיק כי <math>||S_n||^2\to ||f||^2</math> וזהו בדיוק שיוויון פרסבל. | |||
====הוכחת שיוויון פרסבל כאשר טור הפורייה מתכנס במ"ש==== | |||
*תהי <math>f</math> רציפה בקטע <math>[-\pi,\pi]</math> המקיימת <math>f(-\pi)=f(\pi)</math>, כך שהנגזרת שלה <math>f'</math> רציפה למקוטעין. | |||
*נסמן <math>d_n=\sup_{[-\pi,\pi]}|f-S_n|</math> | |||
*הוכחנו כי טור הפורייה של f מתכנס אליה במ"ש, כלומר <math>d_n\to 0</math>. | |||
*לכן <math>||f-S_n||^2 = \frac{1}{\pi}\int_{-\pi}^{\pi} |f-S_n|^2dx \leq 2d_n^2 \to 0</math> | |||
=====דוגמא===== | |||
*הפונקציה <math>f(x)=x^2</math> מקיימת את דרישות המשפט. | |||
*נזכור כי טור הפורייה שלה הוא: | |||
:<math>\frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4(-1)^n}{n^2}cos(nx)</math> | |||
*לכן לפי שיוויון פרסבל נקבל כי: | |||
:<math>\frac{1}{\pi}\int_{-\pi}^{\pi} x^4dx = \frac{4\pi^4}{18}+\sum_{n=1}^\infty \frac{16}{n^4}</math> | |||
:<math>\frac{2\pi^4}{5}-\frac{4\pi^4}{18} = \sum_{n=1}^\infty \frac{16}{n^4}</math> | |||
*ולכן: | |||
:<math>\sum_{n=1}^\infty \frac{1}{n^4} = \frac{\pi^4}{90}</math> | |||
====הוכחת שיוויון פרסבל במקרה הכללי==== | |||
*תהי <math>f \in E</math>, אנחנו מעוניינים להוכיח כי <math>||f-S_m||\to 0</math>. | |||
*נבנה סדרת פונקציות <math>f_n</math> רציפות בקטע <math>[-\pi,\pi]</math> המקיימות <math>f_n(-\pi)=f_n(\pi)</math>, כך שהנגזרות שלהן <math>f_n'</math> רציפות למקוטעין, המקיימות: | |||
:<math>||f-f_n||\to 0</math> | |||
*יהי <math>\varepsilon</math>, נבחר <math>n</math> כך ש <math>||f-f_n||< \frac{\varepsilon}{2}</math>. | |||
*נסמן ב<math>T_m</math> את סדרת הסכומים החלקיים של טור הפורייה של <math>f_n</math>. | |||
*ראינו כי <math>\lim_{m\to\infty}||f_n-T_m||=0</math>. | |||
*כיוון שההיטל הוא הוקטור הקרוב ביותר, נקבל: | |||
**<math>||f-S_m||\leq ||f-T_m||</math> | |||
*כמו כן, <math>||f-T_m||\leq ||f-f_n||+||f_n-T_m||</math> | |||
*קיים מקום החל ממנו לכל <math>m</math> מתקיים כי <math>||f_n-T_m||< \frac{\varepsilon}{2}</math>. | |||
*לכן החל ממקום זה <math>||f-S_m||<\varepsilon</math> כפי שרצינו. | |||
=====בניית סדרת הפונקציות===== | |||
*f רציפה למקוטעין, ולכן רציפה במ"ש בכל קטע רציפות. | |||
*לכן ניתן לבחור חלוקה <math>P</math> הכוללת את נקודות אי הרציפות, עם פרמטר חלוקה מספיק קטן כך ש <math>|f(x)-f(c_k)|^2< \frac{\varepsilon}{2\pi}</math> לכל זוג נקודות <math>x,c_k\in [x_{k-1},x_k]</math>. | |||
*נבחר נקודות כלשהן <math>c_k</math> בכל קטע ונביט בפונקצית המדרגות g שבכל תת קטע שווה לקבוע <math>f(c_k)</math>. | |||
*כעת האינטגרל תמיד קטן מסכום הדרבו העליון: | |||
**<math>\int_{-\pi}^{\pi} |f-g|^2dx \leq \sum_{k=1}^n \sup_{[x_{k-1},x_k]}|f(x)-f(c_k)|^2 (x_k-x_{k-1}) \leq \sum_{k=1}^n \frac{\varepsilon}{2\pi}(x_k-x_{k-1}) = \varepsilon</math> | |||
*לכן אפשר לבנות סדרת פונקציות מדרגות כנ"ל <math>g_n</math> כך ש<math>||f-g_n||<\frac{1}{n}</math> | |||
*כעת נגדיר סדרת פונקציות <math>f_n</math> להיות <math>g_n</math>, פרט לשינויים הבאים: | |||
**עבור <math>\delta</math> שנקבע בהמשך, נחבר בקו ישר את הנקודות בקצוות המקטעים <math>[x_k-\delta,x_k]</math>. | |||
**נגדיר <math>f_n(-\pi)=g(\pi)</math>. | |||
**נחבר בקו ישר את הנקודות בקצה הקטע <math>[x_0,x_0+\delta]</math>. | |||
*עבור <math>\delta</math> קטנה מספיק, <math>\int_{-\pi}^{\pi}|f_n-g|^2dx < \frac{1}{n}</math>. | |||
*סה"כ נקבל כי | |||
**<math>f_n</math> מורכבת מקטעים ישרים המחוברים זה לזה, ולכן מדובר בפונקציה רציפה, בעלת נגזרת רציפה למקוטעין. | |||
**<math>f_n(-\pi)=f_n(\pi)</math> | |||
**אכן מתקיים כי <math>||f-f_n||\leq ||f-g||+||g-f_n||\to 0</math> | |||
===יחידות טור פורייה=== | |||
====הם ישנן שתי פונקציות שונות בעלות אותו טור פורייה?==== | |||
*תהיינה <math>f,g\in E</math> בעלות אותם מקדמי פורייה. | |||
*אם טורי הפורייה מתכנסים לפונקציה, ברור שזו אותה הפונקציה, אבל אם לא? | |||
*מקדמי הפורייה של <math>f-g</math> הם אפס, ולכן לפי שיוויון פרסבל: | |||
:<math>||f-g||^2=0</math> | |||
*לכן <math>f=g</math>. | |||
*שימו לב שעבור סתם פונקציות רציפות למקוטעין, זה אומר ש<math>f=g</math> פרט למספר סופי של נקודות. | |||
====האם תתכן פונקציה אחת, בעלת שני טורים טריגונומטריים?==== | |||
*קנטור הוכיח שאם טור טריגונומטרי שווה לאפס בכל הקטע <math>[-\pi,\pi]</math>, אזי כל מקדמי הטור הם אפס. | |||
*יותר מאוחר הוכיחו כי אם הטור מתאפס בכל נקודה בקטע פרט לקבוצה בת מנייה של נקודות, עדיין כל מקדמי הטור הם אפס. | |||
*מנשוב מצא ב1916 טור טריגונומטרי שמתכנס לאפס בכל נקודה פרט לקבוצה ממידה אפס של נקודות, אך '''לא''' כל מקדמי הטור הם אפס. | |||
==הרצאה 5 - תופעת גיבס, טורי הסינוסים והקוסינוסים== | |||
===תופעת גיבס=== | |||
*ראינו תנאים בהם טור הפורייה מתכנס במ"ש. | |||
*כעת אנחנו רוצים לחקור מקרים בהם אין התכנסות במ"ש, ונראה כי בהן יש חריגה מיוחדת של סדרת הסכומי החלקיים מן הפונקציה. | |||
*נביט בטור פורייה של הפונקציה x: | |||
:<math>\sum_{n=1}^\infty \frac{2(-1)^{n+1}}{n}\sin(nx)</math> | |||
*נסמן ב<math>S_m</math> את סדרת הסכומים החלקיים של הטור ונביט ב: | |||
:<math>S_m(\pi - \frac{\pi}{m})=\sum_{n=1}^m \frac{2(-1)^{n+1}}{n}\sin(n(\pi - \frac{\pi}{m})) = \sum_{n=1}^m \frac{2}{n}\sin(\frac{n\pi}{m})</math> | |||
*כעת, | |||
:<math>\sum_{n=1}^m \frac{2}{n}\sin(\frac{n\pi}{m}) = 2\sum_{n=1}^m \frac{\sin\left(\frac{n\pi}{m}\right)}{\left(\frac{n\pi}{m}\right)}\frac{\pi}{m}\to 2\int_0^\pi \frac{\sin(x)}{x}dx</math> | |||
*לכן סה"כ השגיאה בקירוב ע"י הסכומים החלקיים בסדרת הנקודות הללו היא: | |||
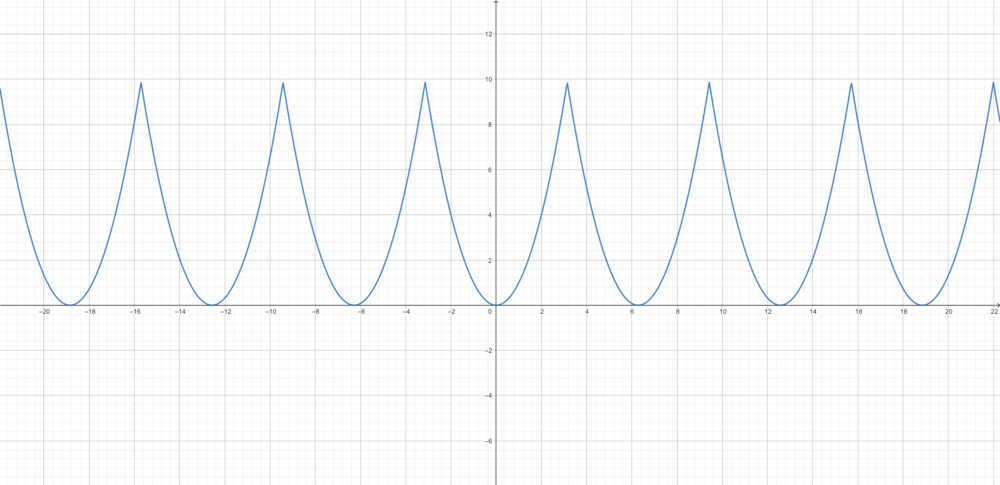
:<math>\pi-\frac{\pi}{m} - S_m (\pi-\frac{\pi}{m}) \to \pi - 2\int_0^\pi \frac{\sin(x)}{x}dx = \int_0^\pi (1-\frac{2\sin(x)}{x})dx \approx -0.56</math> | |||
*(הערכת האינטגרל נעשית על ידי פיתוח טור הטיילור של הפונקציה, נקבל טור לייבניץ לפיו קל לבצע הערכת שגיאה.) | |||
*כלומר סדרת הסכומים החלקיים עולה משמעותית מעל הפונקציה, כפי שניתן לראות בגרף המצורף. | |||
*אם נחלק את זה בגודל הקפיצה בין הגבולות החד צדדים של ההמשך המחזורי של x בנקודה <math>\pi</math>, נקבל בערך <math>-0.089</math>. | |||
*לא נוכיח זאת, אבל יחס הטעות הזה בנקודות אי הרציפות נשמר באופן כללי עבור פונקציות בE שנגזרתן רציפה למקוטעין, ונקרא 'תופעת גיבס'. | |||
:[[קובץ:gibs_x.png|1000px]] | |||
===טור הסינוסים וטור הקוסינוסים=== | |||
*עבור פונקציה <math>f</math> הרציפה בקטע <math>[0,\pi]</math> ובעלת נגזרת רציפה למקוטעין, ניתן להשלים אותה לפונקציה <math>f^+</math> הזוגית בקטע <math>[-\pi,\pi]</math>, או ל<math>f^-</math> האי זוגית בקטע <math>[-\pi,\pi]</math>. | |||
*את ההמשך הזוגי אפשר לפתח לטור קוסינוסים, שמתכנס במ"ש בקטע <math>[0,\pi]</math>. זה נקרא '''טור הקוסינוסים''' של הפונקציה <math>f</math>. | |||
*הוכחה: | |||
**<math>f^+</math> רציפה ב<math>[-\pi,\pi]</math>, בעלת נגזרת רציפה למקוטעין, ומתקיים כמובן ש<math>f(-\pi)=f(\pi)</math>. | |||
*את ההמשך האי זוגי אפשר לפתח לטור סינוסים, שמתכנס אל הפונקציה בקטע <math>(0,\pi)</math>. זה נקרא '''טור הסינוסים''' של הפונקציה <math>f</math>. | |||
*אם <math>f(\pi)=f(0)=0</math> אזי טור הסינוסים מתכנס במ"ש בקטע <math>[0,\pi]</math>. | |||
*הוכחה: | |||
**<math>f^-</math> רציפה כיוון ש<math>f(0)=0</math>, ומתקיים כי <math>f(-\pi)=-f(\pi)=0=f(\pi)</math>. | |||
*חישוב המקדמים: | |||
*עבור טור הקוסינוסים: | |||
**<math>a_n=\frac{1}{\pi}\int_{-\pi}^{\pi} f^+\cos(nx) dx = \frac{2}{\pi}\int_{0}^{\pi}f\cos(nx)dx </math> | |||
*עבור טור הסינוסים: | |||
**<math>b_n=\frac{1}{\pi}\int_{-\pi}^{\pi} f^-\cos(nx) dx = \frac{2}{\pi}\int_{0}^{\pi}f\sin(nx)dx </math> | |||
====דוגמאות==== | |||
*נחשב טור קוסינוסים של <math>e^x</math>: | |||
**<math>a_0 = \frac{2}{\pi}\int_0^{\pi} e^xdx = \frac{2}{\pi}(e^\pi-1)</math> | |||
**<math>a_n = \frac{2}{\pi}\int_0^{\pi} e^x\cos(nx)dx = \frac{2}{\pi}\frac{e^\pi(-1)^n-1}{n^2+1}</math> | |||
**הטור מתכנס במ"ש לפונקציה בקטע <math>[0,\pi]</math>: | |||
:<math>e^x=\frac{e^\pi-1}{\pi}+ \frac{2}{\pi}\sum_{n=1}^\infty \frac{e^\pi(-1)^n-1}{n^2+1}\cos(nx) </math> | |||
*לכן מותר לבצע אינטגרציה איבר איבר, נחשב את <math>\int_0^x</math> בשני הצדדים ונקבל: | |||
:<math>e^x-1 - \frac{e^\pi-1}{\pi}x = \frac{2}{\pi}\sum_{n=1}^\infty \frac{e^\pi(-1)^n-1}{n^3+n}\sin(nx)</math> | |||
*נציב למשל <math>x=0</math> ונקבל את השיוויון: | |||
:<math>\sum_{n=1}^\infty \frac{e^\pi(-1)^n-1}{n^2+1} = \frac{\pi}{2} - \frac{e^\pi-1}{2}</math> | |||
*נחשב טור סינוסים של <math>e^x</math>: | |||
**<math>b_n=\frac{2}{\pi}\int_0^\pi e^x\sin(nx)dx = \frac{2n(1-e^\pi(-1)^n)}{\pi(n^2+1)}</math> | |||
**הטור מתכנס בקטע <math>(0,\pi)</math>: | |||
:<math>e^x=\sum_{n=1}^\infty \frac{2n(1-e^\pi(-1)^n)}{\pi(n^2+1)}\sin(nx) </math> | |||
*נחשב טור סינוסים של <math>f(x)=\pi x - x^2</math>. | |||
*שימו לב: <math>f(0)=f(\pi)=0</math>. | |||
**<math>b_n=\frac{2}{\pi}\int_0^\pi (\pi x-x^2)\sin(nx)dx = \frac{4(1-(-1)^n)}{\pi n^3} </math> | |||
**לכן הטור מתכנס במ"ש בקטע <math>[0,\pi]</math>: | |||
:<math>\pi x - x^2 = \sum_{n=1}^\infty \frac{4(1-(-1)^n)}{\pi n^3} \sin(nx)</math> | |||
*לכן מותר לבצע אינטגרציה איבר איבר, נחשב את <math>\int_0^x</math> בשני הצדדים ונקבל: | |||
:<math>\frac{\pi x^2}{2} - \frac{x^3}{3} = \sum_{n=1}^\infty \frac{4(1-(-1)^n)}{\pi n^4}(-\cos(nx)+1)</math> | |||
*שימו לב שלא מדובר בטור טריגונומטרי. | |||
==הרצאה 6 - משוואת החום על טבעת, התמרת פורייה== | |||
===משוואת החום על טבעת=== | |||
*נביט במד"ח החום על מוט עבור הפונקציה <math>u(x,t)</math>: | |||
**<math>u_t-ku_{xx}=0</math> | |||
**<math>u(x,0)=f(x)</math> (תנאי התחלה) | |||
**<math>u(-\pi,t)=u(\pi,t)</math> (תנאי שפה) | |||
**<math>u_x(-\pi,t)=u_x(\pi,t)</math> (תנאי שפה) | |||
**כאשר <math>x\in[-\pi,\pi]</math>, ו<math>t\in[0,\infty)</math> | |||
*על מנת להבין את תנאי השפה, אפשר לחשוב על הבעייה במובן שהמוט הוא מעגלי. | |||
*נחפש פתרון מהצורה <math>u(x,t)=X(x)\cdot T(t)</math>. | |||
*נציב במד"ח את הניחוש, ונקבל: | |||
:<math>X(x)T'(t)=kX''(x)T(t)</math> | |||
*נניח שהצדדים שונים מאפס ונחלק: | |||
:<math>\frac{T'(t)}{kT(t)}=\frac{X''(x)}{X(x)}</math> | |||
*כיוון שכל צד תלוי במשתנה אחר, הדרך היחידה לקבל שיוויון היא אם שני הצדדים קבועים. | |||
*נביט בפתרונות עבור קבוע שלילי: | |||
:<math>\frac{T'(t)}{kT(t)}=\frac{X''(x)}{X(x)}=-\lambda</math> | |||
*כעת נפתור את ה[[מד"ר תקציר הרצאות|מד"ר]]ים בנפרד: | |||
*שימו לב שאנו בוחרים את השמות של הקבועים בצורה מיוחדת לקראת הפתרון בהמשך. | |||
**עבור <math>\lambda=0</math>: | |||
***<math>X_0(x)=cx+\frac{a_0}{2}</math>, ועל מנת לקיים את תנאי השפה נקבל כי <math>c=0</math> | |||
***<math>T_0(t)=1</math> (הקבוע יבלע בקבוע של <math>X_0(x)</math>) | |||
**עבור <math>\lambda\neq 0</math>: | |||
***<math>X= a_{\sqrt{\lambda}} \cos(\sqrt{\lambda}x) + b_{\sqrt{\lambda}} \sin(\sqrt{\lambda}x)</math> | |||
***<math>T=e^{-k\lambda t}</math> (הקבוע חסר כי הוא יבלע בקבועים האחרים כאשר נכפול ב<math>X(x)</math>) | |||
*ע"י הצבה ניתן לוודא שעבור <math>\lambda=n^2</math> הפונקציות לעיל מקיימות את תנאי השפה. | |||
*גם צירוף לינארי שלהן יהווה פתרון כיוון שהמד"ח הומוגנית ותנאי השפה הומוגניים. | |||
*צירוף לינארי אינסופי יהווה פתרון לבעייה אם טורי הנגזרות יתכנסו במ"ש (ולכן יהיה מותר לגזור איבר איבר). | |||
*לכן אנו מחפשים פתרון כללי מהצורה: | |||
:<math>u(x,t)=T_0(t)X_0(x)+\sum_{n=1}^\infty T_n(t)X_n(x) = \frac{a_0}{2} + \sum_{n=1}^\infty e^{-kn^2 t}(a_n\cos(nx)+b_n\sin(nx))</math> | |||
*כל שנותר לנו לעשות הוא למצוא את הקבועים <math>a_n,b_n</math>. | |||
*נציב כעת בתנאי ההתחלה <math>u(x,0)=f(x)</math> ונקבל בעצם את טור הפורייה: | |||
:<math>f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx)</math> | |||
*אנחנו יכולים לפתור משוואה זו בהנתן שf מקיימת את תנאי משפט דיריכלה. | |||
*מדוע זה יהיה פתרון? | |||
**נזכור שמקדמי הפורייה שואפים לאפס. | |||
**בזכות האקספוננט, טור זה ונגזרותיו אכן יתכנסו במ"ש עבור <math>t\in [a,\infty)</math> לכל <math>a>0</math> ולכל <math>x\in[-\pi,\pi]</math>. | |||
**לכן מותר לגזור איבר איבר, ואכן מדובר בפתרון של המד"ח. | |||
===התמרת פורייה=== | |||
====טור פורייה המרוכב==== | |||
*לא קשה לוודא כי <math>\{e^{inx}\}_{n\in\mathbb{Z}}</math> מהווה קבוצה אורתונורמלית בE אם נעדכן מעט את המכפלה הפנימית: | |||
:<math>\langle f,g\rangle = \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)\overline{g(x)}dx</math> | |||
*תהי <math>f\in E</math>, שאלה שעולה באופן טבעי היא האם: | |||
:<math>f=\sum_{n=-\infty}^\infty \langle f,e^{inx}\rangle e^{inx}</math> | |||
*כאשר אנו מגדירים את הסכום ממינוס אינסוף עד אינסוף באופן הבא: | |||
:<math>\sum_{n=-\infty}^\infty u_n = u_0+\sum_{n=1}^\infty (u_n+u_{-n}) </math> | |||
*נסמן את מקדמי פורייה הרגילים ב<math>a_n,b_n</math>. | |||
*נשים לב כי עבור <math>n=0</math> נקבל: | |||
:<math>\langle f,1\rangle = \frac{a_0}{2}</math> | |||
*כעת עבור <math>n>0</math> מתקיים: | |||
:<math>\langle f, e^{inx}\rangle e^{inx}+\langle f, e^{-inx}\rangle e^{-inx} =</math> | |||
:<math>= (\langle f, e^{inx}\rangle+\langle f, e^{-inx}\rangle)\cos(nx) + (\langle f, e^{inx}\rangle-\langle f, e^{-inx}\rangle)i\sin(nx)=</math> | |||
:<math>= 2\langle f, \cos(nx)\rangle \cos(nx) + 2\langle f, i\sin(nx)\rangle i\sin(nx)= </math> | |||
:<math>=a_n\cos(nx)+b_n\sin(nx)</math> | |||
*(שימו לב: הi יצא מהצד הימני של המכפלה הפנימית עם מינוס) | |||
*כלומר, טור פורייה המרוכב הוא בדיוק טור פורייה הרגיל! | |||
====הכללה לפונקציות שאינן מחזוריות==== | |||
*טורי פורייה עזרו לנו לחקור פונקציות בקטע <math>[-\pi,\pi]</math>. | |||
*בהנתן גל <math>e^{inx}</math>, מצאנו את ה'אמפליטודה' שלו (המקדם): | |||
:<math>\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)e^{-inx}dx</math> | |||
*(שימו לב - המכפלה הפנימית מצמידה את הפונקציה מימין, ולכן קיבלנו <math>-i</math>). | |||
*מחשבה הגיונית היא שאם נרצה לחקור פונקציות בכל הממשיים, עבור גל <math>e^{isx}</math> נמצא את ה'אמפליטודה': | |||
:<math>\mathcal{F}[f](s)=\frac{1}{2\pi}\int_{-\infty}^\infty f(x)e^{-isx}dx</math>. | |||
*כאשר האינטגרל מתכנס, הפונקציה <math>\mathcal{F}[f](s)</math> נקראת '''התמרת פורייה''' של הפונקציה <math>f</math>. | |||
*הערה - המקדם <math>\frac{1}{2\pi}</math> לעיתים אינו מופיע בהגדרת ההתמרה. אנחנו נראה בהמשך שיש לו קשר להתמרה ההפוכה. | |||
*הערות כלליות: | |||
**נסמן בדר"כ את ההתמרה של f ב<math>F(s)=\mathcal{F}(f)(s)</math>. | |||
**<math>F(s)</math> מייצגת את האמפליטודה בכל תדר, ולכן נהוג לומר שהיא מוגדרת ב'מרחב התדר'. | |||
**לעומת זאת, <math>f(x)</math> מייצגת את גובה הפונקציה בכל נקודה בזמן, ונהוג לומר שהיא מוגדרת ב'מרחב הזמן'. | |||
**לכל תדר <math>s</math> יש שני גלים שמייצגים אותו, <math>e^{\pm isx}</math>. | |||
**כפי שלמדנו, באמצעות שני הגלים ניתן לייצג כל 'פאזה'. | |||
*נסמן ב<math>G</math> את אוסף הפונקציות <math>g</math> הרציפות למקוטעין ב<math>\mathbb{R}</math>, עבורן האינטגרל הלא אמיתי מתכנס <math>\int_{-\infty}^\infty|g(x)|dx<\infty</math>. | |||
*לכל <math>f\in G</math> התמרת הפורייה מוגדרת בכל הממשיים. | |||
**הוכחה: | |||
**<math>\int_{-\infty}^\infty|f(x)e^{-isx}|dx = \int_{-\infty}^\infty|f(x)|dx</math> מתכנס. | |||
**כיוון שהאינטגרל המגדיר את <math>F(s)</math> מתכנס בהחלט, הוא מתכנס. | |||
=====דוגמאות===== | |||
*נמצא את <math>\mathcal{F}(f)(s)</math> עבור <math>f(x)=e^{-|x|}</math>. | |||
:<math>2\pi F(s)=\int_{-\infty}^\infty e^{-|x|}e^{-isx}dx = \int_0^\infty e^{-x}e^{-isx}dx + \int_{-\infty}^0 e^{x}e^{-isx}dx=</math> | |||
:<math>=\left[\frac{e^{-x(1+is)}}{-(1+is)}\right]_0^\infty + \left[\frac{e^{x(1-is)}}{1-is}\right]_{-\infty}^0=\frac{1}{1+is} + \frac{1}{1-is} = \frac{2}{1+s^2}</math> | |||
*שימו לב - השתמשנו בעובדה ש<math>e^{isx}</math> חסומה, ואילו <math>e^{-x}\to 0</math> כאשר <math>x\to \infty</math>. | |||
*לכן סה"כ קיבלנו כי <math>\mathcal{F}[e^{-|x|}](s) = \frac{1}{\pi(1+s^2)}</math> | |||
*נמצא את התמרת הפורייה של <math>f(x)=\begin{cases}|x| & |x|\leq \pi \\ 0 & |x|>\pi\end{cases}</math> | |||
:<math>F(s)=\frac{1}{2\pi}\int_{-\infty}^\infty f(x)e^{-isx}dx = \frac{1}{2\pi}\int_{-\pi}^\pi |x|e^{-isx}dx = </math> | |||
:<math>\frac{1}{2\pi}\int_{-\pi}^\pi |x|\cos(sx)dx - \frac{i}{2\pi}\int_{-\pi}^\pi |x|\sin(sx)dx = \frac{1}{\pi}\int_{0}^\pi x\cos(sx)dx = \frac{\sin(s\pi)}{s} + \frac{\cos(s\pi)-1}{s^2\pi}</math> | |||
*שימו לב: חישוב האינטגרל שגוי עבור <math>s=0</math>, ניתן להציבו בנוסחא המקורית של האינטגרל או להשתמש ברציפות ההתמרה, שנלמד בהמשך. | |||
==הרצאה 7 - תכונות של התמרות פורייה== | |||
===תכונות ההתמרה=== | |||
*תהי <math>f\in G</math> אזי <math>F(s)=\mathcal{F}[f](s)</math> רציפה במ"ש ב<math>\mathbb{R}</math>. | |||
**הוכחה: | |||
**יהי <math>\varepsilon>0</math>. כיוון ש <math>\int_{-\infty}^{\infty}|f(x)|dx</math> מתכנס, קיים <math>R</math> עבורו <math>\frac{1}{2\pi}\int_{|x|>R}|f(x)|dx <\frac{\varepsilon}{4}</math> | |||
**עבור <math>s_1,s_2</math> מתקיים כי <math>|F(s_1)-F(s_2)|\leq \frac{1}{2\pi}\int_{-\infty}^{\infty}|f(x)(e^{-is_1x}-e^{-is_2x})|dx</math> | |||
**כמובן ש <math>|e^{-is_1x}-e^{-is_2x}|\leq 2</math> ולכן בתחום <math>|x|>R</math> האינטגרל הנ"ל קטן מ<math>\frac{\varepsilon}{2}</math>. | |||
**נותר להוכיח שעבור <math>s_1,s_2</math> מספיק קרובים מתקיים כי <math>\frac{1}{2\pi}\int_{-R}^{R}|f(x)(e^{-is_1x}-e^{-is_2x})|dx<\frac{\varepsilon}{2}</math> | |||
**נראה כי <math>|e^{ix}-e^{iy}|\leq |x-y|</math>. | |||
***<math>|e^{ix}-e^{iy}|</math> הוא המרחק בין שתי נקודות על מעגל היחידה. | |||
***<math>|x-y|</math> הוא הזווית בינהן, כלומר אורך הקשת בינהן. | |||
***אורך הקשת בוודאי גדול או שווה למרחק הישר בין שתי הנקודות. | |||
**לכן <math>|e^{-is_1x}-e^{-is_2x}|\leq |x||s_1-s_2|</math> | |||
**כיוון ש<math>|x|\leq R</math> והפונקציה <math>f</math> חסומה בתחום זה, עבור <math>|s_1-s_2|</math> מספיק קטן נקבל את הדרוש. | |||
*רשימת תכונות נוספות של ההתמרה: | |||
*<math>\mathcal{F}[f+a\cdot g] = \mathcal{F}[f]+a\mathcal{F}[g]</math> | |||
*<math>\mathcal{F}[f](-s) = \overline{\mathcal{F}[f](s)}</math> | |||
*אם <math>f</math> ממשית וזוגית, גם <math>\mathcal{F}[f](s)</math> ממשית וזוגית. | |||
*הזזה במרחב הזמן: | |||
*אם <math>g(x)=f(ax+b)</math>, אזי <math>\mathcal{F}(g)(s) = \frac{1}{|a|}e^{\frac{isb}{a}}\mathcal{F}[f](\frac{s}{a})</math> | |||
*אם <math>a=1</math> אז נקבל שהזזה במרחב הזמן שקולה לסיבוב במרחב התדר (כפל ב<math>e^{isb}</math> משנה את הזוית). | |||
*הזזה במרחב התדר: | |||
*<math>\mathcal{F}[e^{ibx}f(x)](s) = \mathcal{F}[f](s-b)</math> | |||
*באופן דומה, קיבלנו שסיבוב בזמן שקול להזזה בתדר. | |||
*התמרת הנגזרת: | |||
*נניח <math>f,f'\in G</math> ונניח כי <math>f'</math> רציפה ומתקיים כי <math>\lim_{x\to \pm\infty}f(x)=0</math>, אזי: | |||
*<math>\mathcal{F}[f'](s)=is\mathcal{F}[f](s)</math> | |||
**הוכחה: | |||
**<math>\mathcal{F}[f'](s) = \frac{1}{2\pi}\int_{-\infty}^{\infty} f'(x)e^{-isx}dx</math> | |||
**נבצע אינטגרציה בחלקים ונקבל כי | |||
**<math>\mathcal{F}[f'](s) = \frac{1}{2\pi}(fe^{-isx})_{-\infty}^{\infty} + \frac{is}{2\pi} \int_{-\infty}^{\infty} f(x)e^{-isx}dx</math>. | |||
**כיוון ש<math>e^{-isx}</math> חסומה, יחד עם הנתון נובע כי <math>(fe^{-isx})_{-\infty}^{\infty}=0</math>. | |||
**לכן סה"כ קיבלנו כי <math>\mathcal{F}[f'](s)=is\mathcal{F}[f](s)</math> | |||
*נגזרת ההתמרה: | |||
*תהי <math>f\in G</math> רציפה כך ש<math>xf(x)\in G</math> אזי: | |||
*<math>\mathcal{F}[xf(x)](s)=i\frac{d}{ds}\mathcal{F}[f](s)</math> | |||
**הוכחה: | |||
**<math>i\frac{d}{ds}\mathcal{F}[f](s) = i \frac{d}{ds} \frac{1}{2\pi}\int_{-\infty}^{\infty} f(x)e^{-isx}dx = \frac{i}{2\pi}\int_{-\infty}^{\infty} f(x)\frac{d}{ds}e^{-isx}dx = \frac{-i^2}{2\pi}\int_{-\infty}^{\infty} xf(x)e^{-isx} = \mathcal{F}[xf(x)](s)</math> | |||
**אנחנו צריכים להצדיק את ההכנסה של הנגזרת אל תוך האינטגרל: | |||
***נסמן <math>F_n(s)=\frac{1}{2\pi}\int_{-n}^{n} f(x)e^{-isx}dx</math> | |||
***ברור ש<math>F_n(s)\to F(s)</math>, נוכיח שסדרת הנגזרות מתכנסת במ"ש ולכן מתכנסת לנגזרת של <math>F(s)</math>. | |||
***עבור אינטגרל סופי מותר להחליף את סדר הנגזרת והאינטגרל בזכות פוביני. | |||
***אכן <math>F_n'(s)</math> מתכנסות במ"ש כיוון שהאינטגרל <math>\int_{-\infty}^\infty |xf(x)|dx</math> מתכנס, והרי <math>|xf(x)e^{-isx}|=|xf(x)|</math> ואכן אינו תלוי בs. | |||
====דוגמאות==== | |||
*ראינו כי <math>\mathcal{F}[e^{-|x|}](s) = \frac{1}{\pi(1+s^2)}</math> | |||
*לכן על ידי הזזה בזמן נקבל כי: | |||
**<math>\mathcal{F}[e^{-|1-2x|}](s) = \frac{e^{\frac{-is}{2}}}{2\pi (1+(-\frac{s}{2})^2)}</math> | |||
*נסמן <math>F(s)=\mathcal{F}[e^{-x^2}]</math>. | |||
*כעת <math>\mathcal{F}[xe^{-x^2}] = iF'</math> לפי הנוסחא של נגזרת ההתמרה. | |||
*מצד שני, <math>\mathcal{F}[-2xe^{-x^2}] = isF</math> לפי הנוסחא של התמרת הנגזרת. | |||
*ביחד נקבל כי <math>isF = -2iF'</math>, ולכן <math>sF=-2F'</math>. | |||
*נפתור את המד"ר: | |||
**נכפול בגורם אינטגרציה <math>\frac{1}{2}e^{\frac{s^2}{4}}</math> ונקבל <math>(e^{\frac{s^2}{4}}F)'=0</math> | |||
**לכן <math>F=Ce^{-\frac{s^2}{4}}</math> | |||
**נציב <math>s=0</math> | |||
**<math>2\pi C=F(0)=\int_{-\infty}^\infty e^{-x^2}dx </math>, נחשב אינטגרל מפורסם זה בהמשך. | |||
==הרצאה 8 - התמרה הפוכה== | |||
*בטורי פורייה, מקדמי הפורייה היו האמפליטודות של התדרים, וכאשר סכמנו את הגלים קיבלנו חזרה את הפונקציה לפי משפט דיריכלה. | |||
*כעת התדרים שלנו הם כל הממשיים, ולכן הסכימה שלהם היא בעצם אינטגרל. | |||
*האמפליטודה של כל תדר מרוכב <math>e^{isx}</math> היא התמרת הפורייה <math>F(s)</math>, ולכן אנחנו מצפים לקבל: | |||
**<math>f(x)=\int_{-\infty}^\infty F(s)e^{isx}ds=\mathcal{F}^{-1}[F](x)</math> | |||
*משפט ההתמרה ההפוכה: | |||
**תהי <math>f\in G</math>, אזי בכל נקודה בה קיימות הנגזרות החד צדדיות מתקיים כי: | |||
**<math>\frac{f(x^+)+f(x^-)}{2}=\lim_{n\to\infty}\int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\mathcal{F}[f](s)e^{isx}ds</math> | |||
**שימו לב שהאינטגרל <math>\int_{-\infty}^{\infty}\mathcal{F}[f](s)e^{isx}ds</math> לא חייב להתכנס, אבל אם הוא מתכנס הוא שווה לגבול לעיל. | |||
===דוגמא=== | |||
*ראינו ש<math>\mathcal{F}[e^{-x^2}] = Ce^{-\frac{s^2}{4}} =\frac{1}{2\pi}\int_{-\infty}^\infty e^{-x^2}e^{-isx}dx</math> | |||
*כיוון ש<math>e^{-x^2}</math> רציפה וגזירה, וכיוון ש <math>e^{-\frac{s^2}{4}}\in G</math> לפי משפט ההתמרה ההפוכה נקבל כי: | |||
**<math>\mathcal{F}^{-1}[Ce^{-\frac{s^2}{4}}](x) = e^{-x^2}</math> | |||
*כלומר <math>e^{-x^2}=\int_{-\infty}^\infty Ce^{-\frac{s^2}{4}}e^{isx}ds </math> | |||
*נציב <math>t=\frac{s}{2}</math> ונקבל: | |||
**<math>e^{-x^2} = 2C\int_{-\infty}^\infty e^{-t^2}e^{-i(-2x)t}dt = 2C\cdot 2\pi Ce^{-\frac{(-2x)^2}{4}}</math> | |||
*ולכן <math>4C^2\pi = 1</math>, ומכאן <math>C=\frac{1}{2\sqrt{\pi}}</math> | |||
*נזכור בנוסף שראינו כי <math>2\pi C = \int_{-\infty}^\infty e^{-x^2}dx</math>. | |||
*לכן נובע כי <math>\int_{-\infty}^\infty e^{-x^2}dx = \sqrt{\pi}</math> | |||
===דוגמא=== | |||
*נביט ב<math>f(x)=\begin{cases}1 & |x|<1 \\ 0 & |x|>1\end{cases}</math> | |||
*<math>\mathcal{F}[f](s) = \frac{sin(s)}{\pi s}</math> | |||
*<math>\lim \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}} \frac{sin(s)}{\pi s}e^{is}ds = \frac{1}{2}</math> (הצבנו x=1, הנקודה בה f אינה רציפה). | |||
===הקדמה לקראת הוכחת משפט ההתמרה ההפוכה=== | |||
*כעת נוכיח מספר טענות הדרושות לנו לצורך הוכחת משפט ההתמרה ההפוכה. | |||
====למת רימן-לבג==== | |||
*ראינו גרסא של למת רימן-לבג עבור טורי פוריה, לפי מקדמי הפורייה שואפים לאפס. | |||
*כעת ננסח ונוכיח גרסא עבור התמרות פורייה: | |||
*תהי <math>f\in G</math>, אזי <math>\lim_{s\to\pm\infty}\mathcal{F}[f](s)=0</math> | |||
*(כלומר, האמפליטודות שואפות לאפס כאשר התדר שואף לאינסוף) | |||
*נוכיח את הלמה: | |||
*צ"ל כי<math>\lim_{s\to\pm\infty}\frac{1}{2\pi}\int_{-\infty}^\infty f(x)e^{-isx}dx =0</math> | |||
*נשים לב כי <math>e^{-isx}=\cos(sx)-i\sin(sx)</math>. | |||
*לכן מספיק לנו להוכיח כי <math>\lim_{s\to\pm\infty}\frac{1}{2\pi}\int_{-\infty}^\infty f(x)\cos(sx)dx =0</math> (ההוכחה עבור סינוס דומה). | |||
*כיוון ש<math>f\in G</math> האינטגרל <math>\int_{-\infty}^{\infty}|f(x)|dx</math> מתכנס. | |||
*לכן קיים <math>M</math> עבורו <math>\int_{|x|>M}|f(x)|dx<\frac{\varepsilon}{2}</math>. | |||
*לכן <math>|\int_{|x|>M}f(x)\cos(sx)dx|\leq \int_{|x|>M}|f(x)|dx < \frac{\varepsilon}{2}</math> | |||
*לכן מספיק לנו להוכיח כי עבור <math>|s|</math> מספיק גדול מתקיים <math>|\int_{-M}^{M}f(x)\cos(sx)dx| < \frac{\varepsilon}{2}</math> | |||
*(עבור <math>M=\pi</math> ו<math>s\in\mathbb{N}</math> כבר הוכחנו טענה זו בעזרת פרסבל, כעת נשתמש בשיטות אחרות.) | |||
*נשים לב כי בכל קטע מתקיים: | |||
**<math>\lim_{s\to\pm\infty}\int_{x_1}^{x_2}\cos(sx)dx = \lim_{s\to\pm\infty}\frac{\sin(sx_2)-\sin(sx_1)}{s}=0</math> | |||
*כיוון ש<math>f</math> רציפה למקוטעין היא אינטגרבילית ב<math>[-M,M]</math>. | |||
*לכן ניתן לבחור פונקצית מדרגות <math>h</math> עבורה מתקיים <math>\int_{-M}^M |f-h|dx < \frac{\varepsilon}{4}</math> (האינטגרל על פונקצית המדרגות הינו סכום דרבו תחתון מספיק קרוב). | |||
*כמו כן מתקיים: | |||
**<math>\int_{-M}^Mh\cos(sx)dx = \sum \int_{x_{i-1}}^{x_i}m_i\cos(sx)dx</math> | |||
**כיוון שמדובר בסכום סופי של ביטויים ששואפים לאפס, הסכום גם שואף לאפס. | |||
*סה"כ <math>\int_{-M}^{M}f(x)\cos(sx)dx = \int_{-M}^{M}(f(x)-h(x))\cos(sx)dx + \int_{-M}^{M}h(x)\cos(sx)dx</math> | |||
**מתקיים כי <math>|\int_{-M}^{M}(f(x)-h(x))\cos(sx)dx|\leq \int_{-M}^{M}|f(x)-h(x)|dx < \frac{\varepsilon}{4}</math> | |||
**עבור <math>|s|</math> מספיק גדול מתקיים כי <math>|\int_{-M}^{M}h(x)\cos(sx)dx|< \frac{\varepsilon}{4}</math> | |||
*סה"כ קיבלנו כי עבור <math>|s|</math> מספיק גדול מתקיים <math>|\int_{-\infty}^{\infty}f(x)\cos(sx)sx|<\varepsilon</math> | |||
====טענת עזר==== | |||
*תהי <math>f\in G</math> ותהי x נק' בה הנגזרות החד צדדיות קיימות, אזי: | |||
:<math>\lim_{n\to\infty} \frac{1}{\pi}\int_0^{\infty} f(x+t)\frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{f(x^+)}{2}</math> | |||
:<math>\lim_{n\to\infty} \frac{1}{\pi}\int_{-\infty}^{0} f(x+t)\frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{f(x^-)}{2}</math> | |||
*נוכיח את הטענה הראשונה, הטענה השנייה דומה. | |||
*נגדיר את הפונקציה <math>g(t)=\begin{cases}\frac{f(x+t)}{t}& x\in [\pi,\infty)\\ 0 & x\in (-\infty,\pi)\end{cases}</math> | |||
*כיוון ש<math>f\in G</math> נובע שגם <math>g\in G</math> הרי <math>\left|\frac{f(x+t)}{t}\right|\leq |f(x+t)|</math> עבור <math>t>\pi</math>. | |||
*לכן לפי למת רימן-לבג נובע כי <math>\lim_{s\to\infty}\int_{-\infty}^{\infty}g(t)\sin(st)dt = 0</math> | |||
*בפרט מתקיים גבול הסדרה: | |||
**<math>\lim_{n\to\infty} \int_{-\infty}^{\infty}g(t)\sin\left((n+\frac{1}{2})t\right)dt =0</math> | |||
*אבל <math>\int_{-\infty}^{\infty}g(t)\sin\left((n+\frac{1}{2})t\right)dt = \int_\pi^\infty \frac{f(x+t)}{t}\sin\left((n+\frac{1}{2})t\right)dt</math> | |||
*לכן נותר להוכיח כי <math>\lim_{n\to\infty}\frac{1}{\pi}\int_0^{\pi} f(x+t)\frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{f(x^+)}{2}</math> | |||
*נגדיר את הפונקציה <math>h(t)=f(x+t)\frac{2\sin(\frac{t}{2})}{t}</math>. | |||
**אם נתקן את אי הרציפות הסליקה של <math>\frac{2\sin(\frac{t}{2})}{t}</math> נקבל טור טיילור שגזיר אינסוף פעמים. | |||
**לכן הפוקנציה <math>h</math> רציפה למקוטעין ובעלת נגזרות חד צדדיות קיימות. | |||
*כעת נשים לב כי: | |||
**<math>\frac{1}{\pi}\int_0^{\pi} f(x+t)\frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{1}{\pi}\int_0^{\pi} h(t)\frac{\sin\left((n+\frac{1}{2})t\right)}{2\sin(\frac{t}{2})}dt | |||
= \frac{1}{\pi}\int_0^{\pi} h(t)D_n(t)dt</math> | |||
**לפי ההוכחה של משפט דיריכלה להתכנסות טורי פורייה, הגבול של הביטוי הזה שווה ל<math>\frac{h(0^+)}{2} = \frac{f(x^+)}{2}</math>. | |||
=====דוגמא===== | |||
*טענה: | |||
:<math>\int_0^\infty \frac{\sin(x)}{x}dx = \frac{\pi}{2}</math> | |||
*הוכחה: | |||
**ראשית, אנו יודעים כי האינטגרל מתכנס לפי מבחן דיריכלה לאינטגרלים לא אמיתיים. | |||
**לכן מתקיים כי <math>\int_0^\infty \frac{\sin(x)}{x}dx =\lim_{n\to\infty} \int_0^{(n+\frac{1}{2})\pi}\frac{\sin(x)}{x}dx</math> | |||
**נבצע הצבה <math>t=\frac{x}{n+\frac{1}{2}}</math> ונקבל כי: | |||
***<math>\int_0^{(n+\frac{1}{2})\pi}\frac{\sin(x)}{x}dx = \int_0^\pi \frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt</math> | |||
**עבור <math>f(x)=1</math>, לפי הוכחת טענת העזר נקבל כי הגבול הוא <math>\frac{\pi}{2}</math> | |||
===הוכחת משפט ההתמרה ההפוכה=== | |||
*<math>\int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\mathcal{F}[f](s)e^{isx}ds = \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\left[\frac{1}{2\pi}\int_{-\infty}^\infty f(y)e^{-isy}dy\right]e^{isx}ds=</math> | |||
*<math>=\frac{1}{2\pi} \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\int_{-\infty}^\infty f(y)e^{is(x-y)}dyds</math> | |||
*נחליף את סדר האינטגרציה (הצדקה בהמשך), ונקבל: | |||
*<math>\frac{1}{2\pi}\int_{-\infty}^\infty\int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}f(y)e^{is(x-y)}dsdy =</math> | |||
*<math>\frac{1}{2\pi}\int_{-\infty}^\infty f(y) \left[\frac{e^{is(x-y)}}{i(x-y)}\right]_{-(n+\frac{1}{2})}^{n+\frac{1}{2}} dy =</math> | |||
*<math>\frac{1}{2\pi}\int_{-\infty}^\infty f(y) \frac{2\sin\left((n+\frac{1}{2})(x-y)\right)}{(x-y)} dy</math> | |||
*נציב <math>t=y-x</math> ונקבל: | |||
*<math>\frac{1}{\pi}\int_{-\infty}^\infty f(x+t) \frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{f(x^+)+f(x^-)}{2}</math> | |||
כאשר המעבר האחרון הוא בזכות טענת העזר לעיל. | |||
====הצדקת החלפת סדר האינטגרציה==== | |||
*נביט בסדרה <math>u_k(s)=\int_{-k}^k f(y)e^{is(x-y)}dy</math>, שמתכנסת כמובן ל<math>\int_{-\infty}^\infty f(y)e^{is(x-y)}dy</math> | |||
*מתקיים כי <math>|\int_{-\infty}^\infty f(y)e^{is(x-y)}dy - u_k(s)| \leq \int_{|y|>k} |f(y)e^{is(x-y)}|dy = \int_{|y|>k} |f(y)|dy\to 0</math> | |||
**(נתון כי <math>f\in G</math>) | |||
*לכן הסדרה מתכנסת במ"ש ומותר לבצע אינטגרציה איבר איבר: | |||
**<math>\int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\int_{-\infty}^\infty f(y)e^{is(x-y)}dyds = \lim_{k\to\infty} \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}} u_k(s)ds</math> | |||
**לפי פוביני מותר לנו להחליף את סדר האינטגרציה ונקבל כי | |||
**<math>\int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\int_{-\infty}^\infty f(y)e^{is(x-y)}dyds = \lim_{k\to\infty} \int_{-k}^k \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}f(y)e^{is(x-y)}dsdy = \int_{-\infty}^\infty \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}f(y)e^{is(x-y)}dsdy</math> | |||
**שימו לב שהאינטגרל הלא אמיתי אכן מתכנס (כפי שהוכחנו לעיל) ולכן שווה לגבול. | |||
==הרצאה 9 - קונבולוציה, משוואת החום על מוט אינסופי== | |||
*תהיינה <math>f,g:\mathbb{R}\to\mathbb{C}</math> פונקציות, נגדיר את ה'''קונבולוציה''' ביניהן להיות: | |||
**<math>f*g(x) = \int_{-\infty}^\infty f(x-y)g(y)dy</math>. | |||
*מוטיבציה לדוגמא: | |||
**אם <math>f,g</math> הן פונקציות צפיפות של משתנים מקריים, מהי פונקציית הצפיפות של סכום המשתנים? | |||
**הסיכוי שסכום המשתנים יהיה x, הוא סכום מכפלות הסיכויים שמשתנה אחד יהיה שווה y והשני יהיה שווה x-y. | |||
*הקונבולוציה היא אבלית: | |||
**<math>g*f = \int_{-\infty}^\infty g(x-y)f(y)dy = \{t=x-y,dt=-dy\} = \int_{-\infty}^\infty g(t)f(x-t)dt = f*g</math> | |||
*שימו לב: בנושא זה נבצע החלפת סדר אינטגרציה, אך לא נצדיק החלפה זו כיוון שהיא דורשת העמקה רבה. | |||
*ניתן להעמיק ע"י קריאה בספר Fourier Analysis של T.W.Korner | |||
*משפט הקונבולוציה: | |||
*תהיינה <math>f,g\in G</math> רציפות וחסומות אזי <math>\mathcal{F}[f*g] = 2\pi \cdot \mathcal{F}[f] \cdot \mathcal{F}[g]</math> | |||
*הסבר המשפט (לא הוכחה מלאה, כיוון שאנו מחליפים סדר אינטגרציה ללא הצדקה): | |||
:<math>\mathcal{F}[f*g] = \frac{1}{2\pi}\int_{-\infty}^\infty \left[\int_{-\infty}^\infty f(x-y)g(y)dy\right]e^{-isx}dx = </math> | |||
:<math>= \frac{1}{2\pi}\int_{-\infty}^\infty \int_{-\infty}^\infty f(x-y)e^{-is(x-y)}g(y)e^{-isy}dydx =</math> | |||
:<math>= \frac{1}{2\pi}\int_{-\infty}^\infty \int_{-\infty}^\infty f(x-y)e^{-is(x-y)}g(y)e^{-isy}dxdy =</math> | |||
:<math>= \frac{1}{2\pi}\int_{-\infty}^\infty \left[\int_{-\infty}^\infty f(x-y)e^{-is(x-y)}dx\right] g(y)e^{-isy}dy =</math> | |||
:<math>= \frac{1}{2\pi}\int_{-\infty}^\infty \left[\int_{-\infty}^\infty f(t)e^{-ist}dt\right] g(y)e^{-isy}dy =</math> | |||
:<math>= 2\pi\left(\frac{1}{2\pi}\int_{-\infty}^\infty f(t)e^{-ist}dt\right) \cdot \left( \frac{1}{2\pi}\int_{-\infty}^\infty g(y)e^{-isy}dy\right) =2\pi \cdot \mathcal{F}[f] \cdot \mathcal{F}[g]</math> | |||
===משוואת החום על מוט אינסופי=== | |||
*אם פונקצית החום על מוט אינסופי היא <math>u(x,t)</math>, היא מקיימת את המשוואה <math>u_t-ku_{xx}=0</math>. | |||
*נניח גם כי תנאי ההתחלה הם <math>u(x,0)=f(x)</math> (זה החום בכל נקודה במוט בזמן 0). | |||
*נבצע התמרת פורייה של הפתרון לפי המשתנה x: | |||
:<math>U(s,t)=\frac{1}{2\pi}\int_{-\infty}^{\infty} u(x,t)e^{-isx}dx</math> | |||
*נגזור לפי המשתנה t: | |||
:<math>U_t(s,t) = \frac{1}{2\pi}\int_{-\infty}^{\infty} u_t(x,t)e^{-isx}dx</math> | |||
*(נניח כי הפתרון מקיים את התנאים שמאפשרים להחליף את סדר הגזירה והאינטגרציה, לא נרחיב על כך בהמשך) | |||
*כיוון ש<math>u_t-ku_{xx}=0</math> נקבל כי: | |||
:<math>U_t(s,t) = \frac{k}{2\pi}\int_{-\infty}^{\infty} u_{xx}(x,t)e^{-isx}dx</math> | |||
*נזכר בנוסחאת התמרת הנגזרת <math>\mathcal{F}[f']=is\mathcal{F}[f]</math> | |||
*ולכן נקבל כי: | |||
:<math>U_t(s,t) = -s^2 \frac{k}{2\pi}\int_{-\infty}^\infty u(x,t)e^{-isx}dx = -ks^2 U(s,t)</math> | |||
*זו מד"ר פשוטה שפתרונה הוא: | |||
:<math>U(s,t) = A(s)e^{-ks^2 t}</math> | |||
*נציב את תנאי ההתחלה <math>t=0</math> ונקבל כי | |||
:<math>A(s) = U(s,0) = \frac{1}{2\pi}\int_{-\infty}^{\infty} u(x,0)e^{-isx}dx = \frac{1}{2\pi}\int_{-\infty}^{\infty} f(x)e^{-isx}dx = \mathcal{F}[f]</math> | |||
*לכן בעצם מתקיים כי <math>U(s,t)= F(s)e^{-ks^2 t}</math> | |||
*קיבלנו שההתמרה של הפתרון היא מכפלה של שתי התמרות, ולכן הפתרון הוא הקונבולוציה של שתי הפונקציות המקוריות. | |||
*נחפש את ההתמרה ההפוכה של <math>e^{-ks^2 t}</math> | |||
*נזכור כי <math>\mathcal{F}[e^{-x^2}] = \frac{1}{2\sqrt{\pi}} e^{-\frac{s^2}{4}}</math> | |||
:<math>\mathcal{F}^{-1}[e^{-ks^2 t}]=\int_{-\infty}^\infty e^{-ks^2 t}e^{isx}ds = \{s=\frac{u}{2\sqrt{kt}}\}=</math> | |||
:<math>=\frac{1}{2\sqrt{kt}}\int_{-\infty}^\infty e^{-\frac{u^2}{4}}e^{iu(\frac{x}{2\sqrt{kt}})}du = \frac{2\sqrt{\pi}}{2\sqrt{kt}} \mathcal{F}^{-1}[\frac{1}{2\sqrt{\pi}}e^{-\frac{u^2}{4}}](\frac{x}{2\sqrt{kt}}) = \frac{\sqrt{\pi}}{\sqrt{kt}}e^{-\frac{x^2}{4kt}}</math> | |||
*נסמן פונקציה זו ב<math>p(x,t)=\frac{\sqrt{\pi}}{\sqrt{kt}}e^{-\frac{x^2}{4kt}}</math> | |||
*לכן עבור פתרון מד"ח החום u מתקיים כי: | |||
:<math>\mathcal{F}[u] = \mathcal{F}[f]\cdot \mathcal{F}[p]</math> | |||
*ולכן לפי משפט הקונבולוציה מתקיים כי | |||
:<math> u(x,t) = \frac{1}{2\pi} f*p(x,t)</math> | |||
*שימו לב שהקונבולוציה היא לפי המשתנה x. | |||
*לכן | |||
:<math>u(x,t) = \frac{1}{2\pi}\int_{-\infty}^\infty f(y)p(x-y,t)dy = \frac{1}{2\sqrt{\pi kt}}\int_{-\infty}^\infty f(y)e^{-\frac{(x-y)^2}{4kt}}dy</math> | |||
*שימו לב שבפתרון הסופי מופיעה פונקצית תנאי ההתחלה, ואין צורך לחשב את ההתמרה שלה. | |||
==הרצאה 10 - משפט הדגימה של שנון== | |||
===משפט הדגימה של שנון=== | |||
*תהי פונקציה f. ברור שבהנתן הערכים של f על השלמים <math>f(0),f(\pm 1),f(\pm 2),...</math> לא ניתן להסיק כלום על ערכיה האחרים (אפילו אם היא רציפה וגזירה). | |||
*בפרט אם נדגום באופן דומה את הפונקציה <math>sin(x)</math> בנקודות <math>2\pi n</math> אנחנו עשויים לחשוד שהיא קבועה לחלוטין. | |||
*מה יקרה אם נדגום גל בקצב מהיר יותר מהתדר שלו? | |||
*במילים פשוטות, משפט הדגימה של שנון אומר שבהנתן פונקציה שהתדרים שלה חסומים, אם נדגום אותה בקצב מהיר פי 2 מהתדר המקסימלי שלה, נוכל לשחזר אותה לחלוטין. | |||
*כעת ננסח את המשפט במדויק, יחד עם ניסוח התנאים הנחוצים על הפונקציות. | |||
*עד כה דיברנו על תדר כמדד לקצב בו הפונקציה חוזרת על עצמה, כעת נגדיר אותו במדויק: | |||
*בהנתן פונקציה עם מחזור <math>t</math> נגדיר את התדר של המחזור להיות <math>\frac{1}{t}</math>. | |||
*דוגמאות: | |||
**התדר של <math>\sin(x)</math> הוא <math>\frac{1}{2\pi}</math> | |||
**התדר של <math>\sin(\pi x)</math> הוא <math>\frac{1}{2}</math> | |||
**באופן כללי, התדר של <math>sin(\pi t x)</math> הוא <math>\frac{t}{2}</math> כיוון ש <math>\sin(\pi t(x+\frac{2}{t})) = \sin(\pi t x)</math> | |||
**התדר של <math>e^{isx}</math> הוא <math>\frac{|s|}{2\pi}</math> כיוון ש <math>e^{is(x+\frac{2\pi}{|s|})} = e^{isx\pm i2\pi} =e^{isx}</math> | |||
*משפט הדגימה של שנון: | |||
*תהי <math>f\in G</math> רציפה ובעלת נגזרת חד צדדיות הקיימות בכל נקודה, שתדריה חסומים על ידי <math>t</math>, אזי בהנתן דגימה שלה בתדר <math>2t</math> ניתן לשחזר אותה בכל הממשיים (כלומר היא נקבעת באופן יחיד על ידי הדגימות). | |||
*שימו לב: הכוונה בכך שתדריה של הפונקציה חסומים, היא למעשה ש<math>\mathcal{F}[f](s)=0</math> לכל <math>\frac{|s|}{2\pi}>t</math>. | |||
====הוכחת משפט הדגימה==== | |||
*כיוון שהתמרת הפורייה מתאפסת מחוץ לקטע <math>[-2\pi t,2\pi t]</math>, ניתן לקבוע כי | |||
:<math>\int_{-\infty}^\infty \mathcal{F}[f](s)e^{isx}ds = \int_{-2\pi t}^{2\pi t}\mathcal{F}[f](s)e^{isx}ds</math> | |||
*ובפרט האינטגרל מתכנס. | |||
*לפי משפט ההתמרה ההפוכה, נובע כי <math>f(x)= \int_{-2\pi t}^{2\pi t}\mathcal{F}[f](s)e^{isx}ds</math> | |||
*כעת, נתונה לנו סדרת הדגימות בתדר <math>2t</math>: | |||
:<math>c_n = f\left(\frac{n}{2t}\right), n\in\mathbb{Z}</math> | |||
*נציב אותן בנוסחא שמצאנו לעיל: | |||
:<math>c_n = \int_{-2\pi t}^{2\pi t}\mathcal{F}[f](s)e^{is\left(\frac{n}{2t}\right)}ds</math> | |||
*נבצע הצבה <math>\frac{s}{2t}=-x</math> ונקבל: | |||
:<math>c_n = \int_{-\pi}^\pi \mathcal{F}[f](-2tx)e^{-inx}dx</math> | |||
*אבל אלה בדיוק מקדמי פוריה (פרט לקבוע <math>\frac{1}{2\pi}</math>) של הפונקציה <math>\mathcal{F}[f](-2tx)</math>. | |||
*כיוון שההתמרה חסומה בתדר, עבור <math>|x|\geq \pi</math> מתקיים כי <math>\mathcal{F}[f](-2tx)=0</math> (זכרו כי ההתמרה רציפה, ולכן מתאפסת גם בקצוות). | |||
*לכן <math>\mathcal{F}[f](-2tx)</math> נקבעת על ידי ערכיה בקטע <math>(-\pi,\pi)</math>, והם נקבעים באופן יחיד על ידי מקדמי הפורייה (מסקנה מפרסבל). | |||
*לבסוף, כפי שראינו לעיל, הפונקציה f נקבעת באופן יחיד על ידי ההתמרה (בזכות משפט ההתמרה ההפוכה). | |||
====הערות==== | |||
*שימו לב שלא ניתן באופן פרקטי לדגום אות אנלוגי באינסוף נקודות. | |||
*מה יקרה אם נדגום במספר סופי של נקודות ונניח כי הפונקציה ממשיכה באופן מחזורי? | |||
*נקבל פונקציה שאינה שייכת ל<math>G</math>, כיוון שהאינטגרל שלה לא יכול להתכנס בכל הממשיים. | |||
*בהמשך, נראה אנלוגיה למשפט הדגימה של שנון בהתמרת פורייה הבדידה. | |||
==הרצאה 11 - התמרת פורייה הבדידה== | |||
===DFT - Discrete Fourier transform=== | |||
*תהי סדרת נקודות <math>a_0,...,a_{N-1} \in \mathbb{C}</math>, התמרת הפורייה הבדידה שלה היא סדרת הנקודות <math>A_0,...,A_{N-1}\in\mathbb{C}</math> המוגדרת ע"י: | |||
:<math>A_n = \sum_{k=0}^{N-1} a_k e^{-2\pi i n\frac{k}{N}} </math> | |||
*שימו לב שכמות הפעולות הנדרשות לחישוב ההתמרה באופן ישיר היא סדר גודל של <math>N^2</math>. | |||
*התמרת פורייה המהירה (FFT) מבצעת את אותו חישוב בכמות פעולות בסדר גודל של <math>N\log(N)</math>. | |||
====משמעות ההתמרה==== | |||
*תהי פונקציה f. נדגום ממנה <math>N</math> נקודות בתדר <math>t</math>, כלומר נתון לנו: | |||
:<math>f(0),f(\frac{1}{t}),f(\frac{2}{t}),...,f(\frac{N-1}{t})</math> | |||
*נסמן נקודות אלה ב<math>a_k=f(\frac{k}{t})</math> | |||
*אנו רוצים לפרק אותה לסכום של גלים: | |||
:<math>f(x)=B_0e^{2\pi i \cdot 0\cdot\frac{t}{N}x}+ B_1e^{2\pi i \cdot 1\cdot\frac{t}{N}x}+B_2e^{2\pi i \cdot 2\cdot\frac{t}{N}x}+...+B_{N-1}e^{2\pi i \cdot (N-1)\cdot\frac{t}{N}x}</math> | |||
*כיוון שהתדר של <math>e^{isx}</math> הוא <math>\frac{|s|}{2\pi}</math> נובע כי הגלים הללו הם בתדרים <math>0,\frac{t}{N},\frac{2t}{N},...,\frac{(N-1)t}{N}</math> | |||
*שימו לב - ככל שנדגום יותר נקודות נקבל יותר מגוון של תדרים. מצד שני, נביט בחלון זמן יותר ארוך ונפספס שינויי תדרים מהירים יותר. | |||
*נוכיח שפירוק זה תמיד אפשרי כך שיהיה שיוויון בכל נקודות הדגימה, ונקשר בין סדרת המקדמים להתמרת הפורייה של נקודות הדגימה. | |||
*נביט בפונקצית הגל <math>u_n(x)=e^{2\pi i n\frac{t}{N}x}</math>. | |||
*נציב בה את נקודות הדגימה ונקבל את הוקטור המרוכב: | |||
:<math>v_n= \left(u_n(0),u_n(\frac{1}{t}),...,u_n(\frac{N-1}{t})\right) = \left( 1,e^{2\pi i n \frac{1}{N}},e^{2\pi i n \frac{2}{N}},...,e^{2\pi i n \frac{N-1}{N}} \right)</math> | |||
*נציב בפונקציה הנתונה f את נקודות הדגימה ונקבל את הוקטור המרוכב: | |||
:<math>v=\left(f(0),f(\frac{1}{t}),f(\frac{2}{t}),...,f(\frac{N-1}{t})\right) = (a_0,...,a_{N-1})</math> | |||
*לכן אנו מעוניינים בפתרון למשוואה: | |||
:<math>v=B_0v_0+...+B_{N-1}v_{N-1}</math> | |||
*זה בדיוק אומר שהפירוק של הפונקציה לגלים מתקיים בכל נקודות הדגימה: | |||
:<math>f(\frac{k}{t}) = B_0u_0(\frac{k}{t})+...+B_{N-1}u_{N-1}(\frac{k}{t})</math> | |||
*נבחן את הקבוצה <math>\{v_0,...,v_{N-1}\}</math>. | |||
:<math>\langle v_n,v_n\rangle = v_n^t \overline{v_n} = \sum_{k=0}^{N-1} e^{2\pi i n \frac{k}{N}}\cdot e^{-2\pi i n \frac{k}{N}}= 1+1+...+1= N</math> | |||
*עבור <math>n\neq m</math>: | |||
:<math>\langle v_n,v_m\rangle = \sum_{k=0}^{N-1} e^{2\pi i n \frac{k}{N}}\cdot e^{-2\pi i m \frac{k}{N}} = \sum_{k=0}^{N-1} e^{2\pi i (n-m) \frac{k}{N}}</math> | |||
*אבל זה בדיוק סכום סדרה הנדסית <math>1+q+...+q^{N-1}</math> עבור <math>q=e^{2\pi i (n-m)\frac{1}{N}}</math> | |||
*שימו לב ש<math>\frac{|n-m|}{N}<1</math> ולכן <math>q\neq 1</math>. | |||
*כמו כן, שימו לב ש<math>q^N = e^{2\pi i (n-m)}=1</math> | |||
*לכן לפי הנוסחא לסכום סדרה הנדסית נקבל כי: | |||
:<math>\langle v_n,v_m\rangle = \frac{1-q^N}{1-q}=0</math> | |||
*כלומר גילינו כי <math>\{v_0,...,v_{N-1}\}</math> קבוצה אורתוגונלית (לא אורתונורמלית) ומהווה בסיס. | |||
*לכן ניתן בקלות לחשב את המקדמים <math>B_n = \frac{\langle v,v_n\rangle}{N}</math> | |||
*לבסוף, נשים לב כי: | |||
:<math>\langle v,v_n\rangle = \sum_{k=0}^{N-1} a_k e^{-2\pi i n \frac{k}{N}} = A_n</math> | |||
*כלומר <math>B_n = \frac{A_n}{N}</math> | |||
====התמרת פורייה הבדידה ההפוכה==== | |||
*מכאן גם ניתן להסיק ישירות את התמרת פורייה ההפוכה, שמחזירה את סדרת המקדמים <math>A_n</math> לסדרת הדגימות <math>a_n</math>. | |||
:<math>v=\frac{1}{N}(A_0v_0+...+A_{N-1}v_{N-1})</math> | |||
*ולכן: | |||
:<math>a_n = \frac{1}{N}\sum_{k=0}^{N-1} A_k e^{2\pi i k \frac{n}{N}}</math> | |||
====מסקנות לגבי גלים ממשיים==== | |||
*פירקנו את הפונקציה לסכום של גלים מרוכבים בנקודות הדגימה, האם ניתן להשתמש בהתמרה על מנת לקבל פירוק לגלים ממשיים? | |||
*ראשית, נשים לב לתופעה הבאה: | |||
:<math>v_{N-n} = (1,e^{2\pi i (N-n) \frac{1}{N}},...,e^{2\pi i (N-n) \frac{N-1}{N}}) = (1,e^{2\pi i (N-n) \frac{1}{N} - 2\pi i },...,e^{2\pi i (N-n) \frac{N-1}{N} - 2\pi i (N-1)})</math> | |||
*(השיוויון נכון בזכות המחזוריות) | |||
*ולכן נקבל: | |||
:<math>v_{N-n} = (1, e^{2\pi i (\frac{(N-n)}{N} - 1)},...,e^{2\pi i (N-1)(\frac{(N-n)}{N} - 1)}) = v_{-n}</math> | |||
*כלומר פירוק הפונקציה לגלים <math>u_0,u_1,...,u_{N-1}</math> נותן את אותם המקדמים כמו פירוק הפונקציה לגלים <math>u_0,u_1,u_{-1},...</math>. | |||
*כאשר המקדם של <math>u_{-n}</math> שווה למקדם של <math>u_{N-n}</math>. | |||
*שימו לב שזה לא פירוק של הפונקציה לסכום הגלים בכל הממשיים, אלא רק בנקודות הדגימה. | |||
*לדוגמא: | |||
*נניח שיש לנו 5 דגימות של f. | |||
*אם נפרק את f לגלים <math>u_0,u_1,...,u_5</math> נקבל <math>v=B_0v_0+...+B_4v_4</math> | |||
*אם נפרק את f לגלים <math>u_{-2},u_{-1},u_0,u_1,u_2</math> נקבל <math>v=B_3v_{-2},B_4v_{-1}+B_0v_0+B_1v_1+B_2v_2</math> | |||
*במצב זה, אם דגמנו בתדר <math>t</math> נקבל את התדרים <math>0,\frac{t}{5},\frac{2t}{5}</math> שזה מתאים למשפט הדגימה של שנון (טווח התדרים של הפונקציה הוא עד חצי מתדר הדגימה). | |||
*עבור n ספציפי מתקיים כי: | |||
:<math>B_ne^{2\pi i n \frac{t}{N}x} + B_{N-n}e^{-2\pi i n \frac{t}{N}x} = (B_n+B_{N-n}) \cos (2\pi n \frac{t}{N}x) + i(B_n-B_{N-n})sin(2\pi n \frac{t}{N}x)</math> | |||
*מהצבה ישירה של הנוסחאות שמצאנו ניתן לראות שאם f ממשית אזי <math>B_n+B_{N-n}</math> וגם <math>i(B_n-B_{N-n})</math> הם ממשיים. | |||
*כלומר הצלחנו לפרק את f לסכום של גלים ממשיים עם מקדמים ממשיים. | |||
*הערה: אם N זוגי, אז הגל <math>u_{\frac{N}{2}}</math> נותר בודד. | |||
*לדוגמא עבור <math>N=4</math> נקבל במקום הגלים <math>u_0,u_1,u_2,u_3</math> את <math>u_{-1},u_0,u_1,u_2</math> | |||
*נשים לב כי במקרה זה <math>v_{\frac{N}{2}}</math> הוא וקטור ממשי (ולכן גם המקדם שלו ממשי) כיוון שהsin מתאפס בכל נקודות הדגימה. | |||
גרסה אחרונה מ־08:15, 16 במאי 2022
מבחנים לדוגמא
תקציר ההרצאות
- ההרצאות מבוססות בחלקן על הספר המצויין 'טורי פוריה' של זעפרני ופינקוס.
עוד ספרים מתמטיים בסגנון ניתן למצוא באתר של סמי זערפני.
הרצאה 1 - הקדמה ומקדמי פוריה
הקדמה - גלים
- מבלי להגדיר גל במפורש, גל הוא תופעה מחזורית.
- לגל שהוא פונקציה במשתנה אחד של ציר הזמן יש שלוש תכונות:
- תדר או אורך גל (אחד חלקי המחזור או המחזור)
- אמפליטודה (מרחק בין המקסימום למינימום)
- פאזה (מהי נק' ההתחלה של המחזור).
- אנחנו נתרכז כמעט באופן בלעדי בפונקציות הטריגונומטריות סינוס וקוסינוס, ונקרא להם גלים טריגונומטריים.
- מדוע דווקא סינוס וקוסינוס?
- למדנו במד"ר על המשוואה [math]\displaystyle{ y''=-k^2y }[/math] המתארת תנועה על מסה המחוברת לקפיץ
- זו למעשה תנועה כללית של גל - ככל שהוא מתרחק, גדל הכוח שמושך אותו למרכז. מיתר גיטרה הוא דוגמא טובה נוספת.
- הפתרון הכללי למד"ר הוא [math]\displaystyle{ y=a\sin(kt)+b\cos(kt) }[/math].
- הקבוע [math]\displaystyle{ k }[/math] קובע את התדר של כל גל.
- הקבועים [math]\displaystyle{ a,b }[/math] קובעים את האמפליטודה של כל גל.
- מה לגבי הפאזה?
- בפונקציה [math]\displaystyle{ a\sin(kt+t_0) }[/math], הקבוע [math]\displaystyle{ t_0 }[/math] קובע את הפאזה.
- ניתן להציג כל גל כזה באמצעות סינוס וקוסינוס ללא פאזה:
- [math]\displaystyle{ a\sin(kt+t_0)=(a\sin(t_0))cos(kt)+(a\cos(t_0))sin(kt) }[/math]
- האם גם ההפך נכון? כלומר האם כל צירוף לינארי [math]\displaystyle{ a\sin(kt)+b\cos(kt) }[/math] ניתן להציג כגל יחיד?
- תשובה: כן.
- הוכחה:
- נסמן [math]\displaystyle{ z=a+bi=rcis(\theta) }[/math]
- כלומר [math]\displaystyle{ a\sin(kt)+b\cos(kt)=r\sin(\theta)sin(kt)+r\cos(\theta)cos(kt)=rcos(kt-\theta) }[/math]
- שימו לב:
- סכמנו שני גלים מאותו תדר עם פאזה אפס, וקיבלנו גל חדש.
- הגל החדש הוא מאותו תדר כמו שני הגלים.
- לגל החדש יש פאזה שאינה אפס.
- האפליטודה של הגל החדש היא [math]\displaystyle{ r=\sqrt{a^2+b^2} }[/math].
- האם כל פונקציה היא סכום של גלים?
- בהנתן פונקציה שהיא סכום של גלים, כיצד נמצא מיהם הגלים המרכיבים אותה?
- האם יש דרך יחידה להרכיב פונקציה מגלים? (למעשה כבר ראינו שלא באופן כללי - הרי הצלחנו להציג גל אחד כסכום של שני גלים אחרים).
- למה בכלל מעניין אותנו לפרק פונקציה לגלים?
- במהלך ההרצאות נענה (לפחות חלקית) על השאלות הללו.
טורי פורייה ומקדמי פוריה
- טור פורייה הוא טור מהצורה [math]\displaystyle{ f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty \left[a_n\cos(nx)+b_n\sin(nx)\right] }[/math]
- אם פונקציה שווה לטור פורייה שלה, מהם המקדמים [math]\displaystyle{ a_n,b_n }[/math]?
חישובים להקדמה
- ראשית נזכור את הנוסחאות הטריגונומטריות:
- [math]\displaystyle{ \sin(a)\sin(b)=\frac{1}{2}\left[\cos(a-b)-\cos(a+b)\right] }[/math]
- [math]\displaystyle{ \cos(a)\cos(b)=\frac{1}{2}\left[\cos(a+b)+\cos(a-b)\right] }[/math]
- כעת, לכל [math]\displaystyle{ 0\neq n\in\mathbb{N} }[/math] נקבל:
- [math]\displaystyle{ \frac{1}{\pi}\int_{-\pi}^{\pi}\sin(nx)\sin(nx)dx = \frac{1}{2\pi}\int_{-\pi}^{\pi}(1-\cos(2nx))dx = \frac{1}{2\pi}\left[x-\frac{1}{2n}\sin(2nx)\right]_{-\pi}^{\pi}=1 }[/math]
- עבור [math]\displaystyle{ n\neq k \in \mathbb{N} }[/math] נקבל:
- [math]\displaystyle{ \int_{-\pi}^{\pi}\sin(nx)\sin(kx)dx = \frac{1}{2}\int_{-\pi}^{\pi}(\cos((n-k)x)-\cos((n+k)x))dx = \frac{1}{2}\left[\frac{\sin((n-k)x)}{n-k}-\frac{\sin((n+k)x)}{n+k}\right]_{-\pi}^{\pi}=0 }[/math]
- שימו לב כי השתמשנו כאן בעובדה ש[math]\displaystyle{ n-k,n+k\neq 0 }[/math].
- באופן דומה, לכל [math]\displaystyle{ 0\neq n\in\mathbb{N} }[/math] נקבל:
- [math]\displaystyle{ \frac{1}{\pi}\int_{-\pi}^{\pi}\cos(nx)\cos(nx)dx = \frac{1}{2\pi}\int_{-\pi}^{\pi}(\cos(2nx)+1)dx = \frac{1}{2\pi}\left[\frac{1}{2n}\sin(2nx)+x\right]_{-\pi}^{\pi}=1 }[/math]
- עבור [math]\displaystyle{ n\neq k \in \mathbb{N} }[/math] נקבל:
- [math]\displaystyle{ \int_{-\pi}^{\pi}\cos(nx)\cos(kx)dx = \frac{1}{2}\int_{-\pi}^{\pi}(\cos((n+k)x)+\cos((n-k)x))dx = \frac{1}{2}\left[\frac{\sin((n+k)x)}{n+k}+\frac{\sin((n-k)x)}{n-k}\right]_{-\pi}^{\pi}=0 }[/math]
- שימו לב כי השתמשנו כאן בעובדה ש[math]\displaystyle{ n-k,n+k\neq 0 }[/math].
- עבור [math]\displaystyle{ n,k\in \mathbb{N} }[/math] נקבל:
- [math]\displaystyle{ \int_{-\pi}^{\pi}\cos(nx)\sin(kx)dx=0 }[/math] כיוון שמדובר באינטגרל בקטע סימטרי על פונקציה אי זוגית.
- ולבסוף, עבור [math]\displaystyle{ n=0 }[/math] נקבל
- [math]\displaystyle{ \frac{1}{\pi}\int_{-\pi}^{\pi}\cos(0)\cos(0)dx=\frac{1}{\pi}\int_{-\pi}^{\pi}1dx=2 }[/math]
- שימו לב שכאשר מציבים 0 בsin מקבלים אפס, ולכן אין צורך בבדיקה הזו.
- כמו כן קל לחשב [math]\displaystyle{ \int_{-\pi}^{\pi} \sin(x)dx = \int_{-\pi}^{\pi} \cos(x)dx=0 }[/math]
- הערה חשובה:
- למעשה כלל החישובים שעשינו לעיל מוכיחים שהקבוצה [math]\displaystyle{ \{\frac{1}{\sqrt{2}},sin(x),cos(x),sin(2x),cos(2x),...\} }[/math] מהווה קבוצה אורתונורמלית לפי המכפלה הפנימית [math]\displaystyle{ \langle f,g\rangle=\frac{1}{\pi}\int_{-\pi}^{\pi}(f\cdot g) dx }[/math]
מקדמי הטור
- כעת תהי פונקציה ששווה לטור פורייה, ועוד נניח שהטור מתכנס במ"ש.
- [math]\displaystyle{ \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(kx)dx = \frac{1}{\pi}\int_{-\pi}^{\pi}\left(\frac{a_0}{2}+\sum_{n=1}^\infty \left[a_n\cos(nx)+b_n\sin(nx)\right]\right)\cos(kx)dx= }[/math]
- [math]\displaystyle{ =\frac{1}{\pi}\int_{-\pi}^{\pi}\left(\frac{a_0}{2}\cos(kx)+\sum_{n=1}^\infty \left[a_n\cos(nx)\cos(kx)+b_n\sin(nx)\cos(kx)\right]\right)dx= }[/math]
- כיוון שהטור מתכנס במ"ש, מותר לנו לעשות אינטגרציה איבר איבר
- [math]\displaystyle{ =\frac{1}{\pi}\int_{-\pi}^{\pi}\frac{a_0}{2}\cos(kx)dx + \sum_{n=1}^\infty \left[\frac{1}{\pi}\int_{-\pi}^{\pi}\left(a_n\cos(nx)\cos(kx)+b_n\sin(nx)\cos(kx)\right)dx\right] }[/math]
- לפי חישובי האינטגרלים לעיל, כמעט הכל מתאפס וסה"כ נקבל:
- [math]\displaystyle{ a_k=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(kx)dx }[/math]
- שימו לב שחישוב זה נכון בפרט עבור [math]\displaystyle{ k=0 }[/math].
- באופן דומה נקבל כי [math]\displaystyle{ b_k=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin(kx)dx }[/math]
- הוכחנו שאם פונקציה שווה לטור פורייה, והטור מתכנס במ"ש, אזי הוא יחיד והמקדמים שלו נקבעים על ידי הנוסחאות לעיל.
- השאלה היא אילו פונקציות שוות לטור פורייה.
- באופן מיידי, ברור שטור פורייה הוא פונקציה עם מחזור [math]\displaystyle{ 2\pi }[/math].
- לכן בדר"כ אנו שואלים האם ההמשך המחזורי של הפונקציה שווה לטור פורייה:
- תהי פונקציה [math]\displaystyle{ f }[/math], נגדיר את ההמשך המחזורי שלה [math]\displaystyle{ g }[/math] על ידי:
- לכל [math]\displaystyle{ k\in\mathbb{Z} }[/math] ולכל [math]\displaystyle{ x\in [-\pi+2\pi k,\pi+2\pi k) }[/math] נגדיר [math]\displaystyle{ g(x)=f(x-2\pi k) }[/math].
- ברור ש [math]\displaystyle{ g(x+2\pi) = g(x) }[/math], כלומר קיבלנו פונקציה מחזורית.
- ניתן גם לרשום בנוסחא מקוצרת [math]\displaystyle{ g(x)=f(x-2\pi\lfloor\frac{x+\pi}{2\pi}\rfloor) }[/math]
- לדוגמא, ההמשך המחזורי של [math]\displaystyle{ x^2 }[/math]:
דוגמא
- נחשב את מקדמי הפורייה של ההמשך המחזורי של [math]\displaystyle{ x^2 }[/math]
- שימו לב, מקדמי הפורייה של פונקציה וההמשך המחזורי שלה זהים, כיוון שערך הפונקציה בנקודה אחת לא משפיע על האינטגרל.
- [math]\displaystyle{ b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}x^2\sin(nx)dx=0 }[/math].
- שימו לב: מקדמי הפורייה של הסינוסים תמיד יתאפסו עבור פונקציה זוגית, ומקדמי הפורייה של הקוסינוסים תמיד יתאפסו עבור פונקציה אי זוגית.
- [math]\displaystyle{ a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}x^2dx =\frac{2}{\pi}\int_{0}^{\pi}x^2dx= \frac{2}{\pi}\left[\frac{1}{3}x^3\right]_{0}^{\pi} = \frac{2\pi^2}{3} }[/math]
- [math]\displaystyle{ a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}x^2\cos(nx)dx=\frac{2}{\pi}\int_{0}^{\pi}x^2\cos(nx)dx =\left\{\begin{array}{lr}f'=\cos(nx) & g=x^2\\ f= \frac{\sin(nx)}{n} & g'=2x\end{array}\right\}= }[/math]
- [math]\displaystyle{ =\frac{2}{\pi}\left[\frac{x^2\sin(nx)}{n}\right]_0^{\pi} - \frac{4}{n\pi}\int_{0}^{\pi}x\sin(nx)dx = - \frac{4}{n\pi}\int_{0}^{\pi}x\sin(nx)dx= \left\{\begin{array}{lr}f'=\sin(nx) & g=x\\ f= -\frac{\cos(nx)}{n} & g'=1\end{array}\right\}= }[/math]
- [math]\displaystyle{ - \frac{4}{n\pi}\left[\frac{-x\cos(nx)}{n}\right]_0^\pi + \frac{4}{n^2\pi}\int_0^\pi \cos(nx)dx=\frac{4\pi\cos(\pi n)}{n^2\pi}+\frac{4}{n^3\pi}\left[sin(nx)\right]_0^\pi = \frac{4(-1)^n}{n^2} }[/math]
- שימו לב כי לכל [math]\displaystyle{ n\in\mathbb{N} }[/math] מתקיים כי [math]\displaystyle{ cos(n\pi)=(-1)^n }[/math]
- סה"כ אם ההמשך המחזורי של [math]\displaystyle{ x^2 }[/math] שווה לטור פורייה שמתכנס במ"ש, אזי טור זה הוא:
- [math]\displaystyle{ \frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4(-1)^n}{n^2}cos(nx) }[/math]
- נניח (ונוכיח בהמשך) שטור זה אכן שווה לפונקציה ונציב [math]\displaystyle{ \pi }[/math].
- [math]\displaystyle{ \pi^2 = \frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4}{n^2} }[/math]
- ונקבל את הסכום המפורסם
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{1}{n^2}=\frac{\pi^2}{6} }[/math]
הרצאה 2 - למת רימן לבג, גרעין דיריכלה
מרחבי מכפלה פנימית שאינם ממימד סופי והיטלים
- פונקציה נקראת רציפה למקוטעין בקטע סופי אם:
- 1. היא רציפה פרט אולי למספר סופי של נקודות.
- 2. הגבולות החד צדדיים הרלוונטיים בכל נקודה הם סופיים.
- למעשה נקודות אי הרציפות היחידות של פונקציה רציפה למקוטעין הן ממין ראשון (קפיצתיות).
- פונקציה נקראת רציפה למקוטעין בקטע כללי, אם ניתן לחלק אותו לקטעים סופיים בהן הפונקציה רציפה למקוטעין.
- E הוא המרחב הוקטורי של כל הפונקציות הרציפות למקוטעין [math]\displaystyle{ f:[-\pi,\pi]\to\mathbb{C} }[/math] מעל השדה [math]\displaystyle{ \mathbb{C} }[/math], המקיימות בנוסף שבכל נקודה ערך הפונקציה שווה לממוצע בין הגבולות החד צדדיים שלה, ובקצוות ערך הנקודה שווה לגבול החד צדדי המוגדר.
- לא קשה להוכיח שאכן מדובר במרחב וקטורי. בעיקר יש לשים לב לכך שסכום פונקציות בקבוצה נשאר בקבוצה.
- [math]\displaystyle{ \langle f,g\rangle=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\overline{g(x)}dx }[/math] היא מכפלה פנימית מעל E.
- [math]\displaystyle{ \langle g,f\rangle = \frac{1}{\pi}\int_{-\pi}^{\pi}g(x)\overline{f(x)}dx = \overline{\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\overline{g(x)}dx} = \overline{\langle f,g\rangle} }[/math]
- [math]\displaystyle{ \langle af+bg,h\rangle = a\langle f,h\rangle + b\langle g,h\rangle }[/math]
- [math]\displaystyle{ \langle f,f\rangle = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\overline{f(x)}dx = \frac{1}{\pi}\int_{-\pi}^{\pi}|f|^2dx }[/math]
- בכל קטע רציפות האינטגרל על פונקציה חיובית הוא אפס אם ורק אם היא אפס.
- כיוון שהפונקציה בכל נקודה שווה לאחד הגבולות החד צדדיים או לממוצע בניהם, נובע שאם האינטגרל לעיל מתאפס הפונקציה חייבת להתאפס לחלוטין.
- נביט בנורמה המושרית [math]\displaystyle{ ||f||^2=\langle f,f\rangle }[/math]
- כעת נוכיח מספר תכונות של היטלים במרחבי מכפלה פנימית.
- יש לנקוט בזהירות מיוחדת בנושא זה, כיוון שאנו עוסקים במרחבים שאינם נוצרים סופית (אין להם בסיס סופי או מימד).
- ייתכן שהוכחתם חלק מהמשפטים הבאים רק עבור מרחבים נוצרים סופית.
- תהי קבוצה אורתונורמלית סופית [math]\displaystyle{ \{e_1,...,e_n\} }[/math], ונקרא למרחב שהיא פורשת W.
- לכל וקטור [math]\displaystyle{ v\in V }[/math] נגדיר את ההיטל של [math]\displaystyle{ v }[/math] על W על ידי [math]\displaystyle{ \widetilde{v}=\sum_{i=1}^n\langle v,e_i\rangle e_i }[/math]
- נוכיח מספר תכונות לגבי ההיטל הזה:
- מתקיים כי [math]\displaystyle{ \langle v,\widetilde{v}\rangle = \langle \widetilde{v},\widetilde{v}\rangle=\sum_{i=1}^n |\langle v,e_i\rangle|^2 }[/math]
- הוכחה:
- [math]\displaystyle{ \langle v,\widetilde{v}\rangle = \langle v,\sum_{i=1}^n\langle v,e_i\rangle e_i\rangle = \sum_{i=1}^n \overline{\langle v,e_i\rangle}\langle v,e_i\rangle = \sum_{i=1}^n |\langle v,e_i\rangle|^2 }[/math]
- [math]\displaystyle{ \langle \widetilde{v},\widetilde{v}\rangle = \langle \sum_{i=1}^n\langle v,e_i\rangle e_i,\sum_{i=1}^n\langle v,e_i\rangle e_i\rangle = \sum_{i=1}^n |\langle v,e_i\rangle|^2 }[/math]
- המעבר האחרון נכון כיוון ש [math]\displaystyle{ \{e_1,...,e_n\} }[/math] אורתונורמלית.
- מתקיים כי [math]\displaystyle{ ||v||^2=||v-\widetilde{v}||^2+||\widetilde{v}||^2 }[/math]
- הוכחה:
- [math]\displaystyle{ \langle v-\widetilde{v},v-\widetilde{v}\rangle = \langle v,v\rangle - \langle v,\widetilde{v}\rangle - \langle \widetilde{v},v\rangle + \langle \widetilde{v},\widetilde{v}\rangle }[/math]
- נזכור כי [math]\displaystyle{ \langle v,\widetilde{v}\rangle = \langle \widetilde{v},\widetilde{v}\rangle }[/math].
- לכן קיבלנו כי [math]\displaystyle{ ||v-\widetilde{v}||^2 = ||v||^2 - ||\widetilde{v}||^2 }[/math]
- מסקנה מיידית: [math]\displaystyle{ ||\widetilde{v}||\leq ||v|| }[/math]
אי שיוויון בסל
- כעת תהי קבוצה אורתונורמלית אינסופית [math]\displaystyle{ \{e_1,e_2,...\} }[/math].
- לכל [math]\displaystyle{ v\in V }[/math] מתקיים כי [math]\displaystyle{ \sum_{i=1}^\infty |\langle v,e_i\rangle|^2 \leq ||v||^2 }[/math]
- הוכחה:
- ראינו שלכל n מתקיים כי [math]\displaystyle{ \sum_{i=1}^n |\langle v,e_i\rangle|^2 \leq ||v||^2 }[/math].
- כלומר סדרת הסכומים החלקיים של הטור החיובי חסומה על ידי [math]\displaystyle{ ||v||^2 }[/math] ולכן הטור מתכנס למספר שקטן או שווה לו.
- בפרט נובע כי
- [math]\displaystyle{ \lim_{n\to\infty}|\langle v,e_i\rangle|=0 }[/math]
למת רימן לבג
- ראינו כי [math]\displaystyle{ \{\sin(x),\cos(x),\sin(2x),\cos(2x),...\} }[/math] היא קבוצה אורתונורמלית ב[math]\displaystyle{ E }[/math] (כרגע אנו לא צריכים את הפונקציה הקבועה).
- כמו כן לכל פונקציה f הגדרנו מקדמי פורייה ע"י:
- לכל [math]\displaystyle{ 1\leq n\in \mathbb{N} }[/math] הגדרנו [math]\displaystyle{ a_n=\langle f,\cos(nx)\rangle }[/math], ו[math]\displaystyle{ b_n=\langle f,\sin(nx)\rangle }[/math]
- נובע מאי שיוויון בסל כי המקדמים שואפים לאפס.
- כלומר:
- [math]\displaystyle{ \lim_{n\to\infty}\frac{1}{\pi}\int_{-\pi}^\pi f(x)\cos(nx)dx = 0 }[/math]
- [math]\displaystyle{ \lim_{n\to\infty}\frac{1}{\pi}\int_{-\pi}^\pi f(x)\sin(nx)dx = 0 }[/math]
- למת רימן-לבג: תהי [math]\displaystyle{ g }[/math] רציפה למקוטעין בקטע [math]\displaystyle{ [0,\pi] }[/math], אזי:
- [math]\displaystyle{ \lim_{n\to\infty}\int_{0}^\pi g(t)\sin\left(\left(n+\frac{1}{2}\right)t\right)dt = 0 }[/math]
- הוכחה:
- [math]\displaystyle{ \int_{0}^\pi g(t)\sin\left(\left(n+\frac{1}{2}\right)t\right)dt = \int_{0}^\pi g(t)\cos(\frac{t}{2})\sin(nt) dt+\int_{0}^\pi g(t)\sin(\frac{t}{2})\cos(nt) dt }[/math]
- נגדיר את שתי הפונקציות [math]\displaystyle{ h_s(t)=\begin{cases}g(t)\sin(\frac{t}{2}) & 0\leq t\leq \pi \\ 0 & -\pi\leq t \lt 0\end{cases} }[/math] ו [math]\displaystyle{ h_c(t)=\begin{cases}g(t)\cos(\frac{t}{2}) & 0\leq t\leq \pi \\ 0 & -\pi\leq t \lt 0\end{cases} }[/math]
- קל לראות כי שתי הפונקציות רציפות למקוטעין. לכן פרט לשינוי במספר סופי של נקודות שלא משפיע על האינטגרל, ניתן להניח כי [math]\displaystyle{ h_c,h_s\in E }[/math].
- ביחד נקבל כי [math]\displaystyle{ \int_{0}^\pi g(t)\sin\left(\left(n+\frac{1}{2}\right)t\right)dt = \int_{-\pi}^\pi h_c(t)\sin(nt)dt + \int_{-\pi}^\pi h_s(t)\cos(nt)dt \to 0 }[/math]
גרעין דיריכלה
- גרעין דיריכלה הוא הפונקציה [math]\displaystyle{ D_n(t)= \frac{\sin\left(\left(n+\frac{1}{2}\right)t\right)}{2\sin(\frac{t}{2})} }[/math]
- טענה: [math]\displaystyle{ D_n(t)=\frac{1}{2}+\sum_{k=1}^n \cos(kt) }[/math] בכל נקודה [math]\displaystyle{ t\neq 2\pi k }[/math]
- הוכחה:
- נכפל ב[math]\displaystyle{ 2\sin(\frac{t}{2}) }[/math] ונקבל בצד שמאל:
- [math]\displaystyle{ \sin(\frac{t}{2}) + 2\sin(\frac{t}{2})\cos(t) + 2\sin(\frac{t}{2})\cos(2t)+...+2\sin(\frac{t}{2})\cos(nt) }[/math]
- נבחין בזהות הטריגונומטרית [math]\displaystyle{ 2\sin(a)\cos(b) = \sin(b+a)-\sin(b-a) }[/math]
- ובפרט [math]\displaystyle{ 2\sin(\frac{t}{2})\cos(kt) = \sin(kt+\frac{t}{2}) - \sin(kt-\frac{t}{2}) }[/math]
- ביחד נקבל [math]\displaystyle{ \sin(\frac{t}{2}) + \sin(t+\frac{t}{2})-\sin(t-\frac{t}{2}) + \sin(2t+\frac{t}{2}) - \sin(2t-\frac{t}{2})+...+\sin(nt+\frac{t}{2}) - \sin(nt-\frac{t}{2}) = \sin(nt+\frac{t}{2}) = \sin\left(\left(n+\frac{1}{2}\right)t\right) }[/math]
- נשים לב כי הפונקציה [math]\displaystyle{ 2\sin(\frac{t}{2}) }[/math] מתאפסת בנקודות [math]\displaystyle{ t=2\pi k }[/math], בנקודות אלו לגרעין דיריכלה יש אי רציפות סליקה.
- זה נכון כיוון שפרט לנקודות אלו מדובר בפונקציה רציפה.
- כמו כן, גרעין דיריכלה מחזורי [math]\displaystyle{ 2\pi }[/math] כיוון שהוא סכום של פונקציות מחזוריות [math]\displaystyle{ 2\pi }[/math].
- נחשב את האינטגרל על גרעין דיריכלה:
- ראשית, לכל [math]\displaystyle{ 1\leq k \in \mathbb{N} }[/math] מתקיים:
- [math]\displaystyle{ \int_0^\pi \cos(kt)dt = \left[\frac{\sin(kt)}{k}\right]_0^\pi = 0 }[/math]
- לכן נקבל:
- [math]\displaystyle{ \frac{1}{\pi}\int_0^\pi D_n(t)dt = \frac{1}{\pi}\int_0^\pi \left[\frac{1}{2} + \cos(t) + \cos(2t)+...+\cos(nt)\right]dt = \frac{1}{\pi}\int_0^\pi \frac{1}{2}dt = \frac{1}{2} }[/math]
הסכומים החלקיים של טור פוריה
- תהיה נקודה x, נביט בסדרת הסכומים החלקיים של טור הפוריה המתאים לפונקציה [math]\displaystyle{ f }[/math] שהיא מחזורית [math]\displaystyle{ 2\pi }[/math]:
- [math]\displaystyle{ S_n = \frac{a_0}{2} + \sum_{k=1}^n a_k\cos(kx)+b_k\sin(kx) }[/math]
- נציב את מקדמי פוריה ונקבל כי:
- [math]\displaystyle{ S_n = \frac{1}{\pi}\int_{-\pi}^\pi \frac{1}{2}f(t)dt + \sum_{k=1}^n \left[\frac{1}{\pi}\int_{-\pi}^\pi f(t)\cos(kt)dt\right]\cos(kx)+\left[\frac{1}{\pi}\int_{-\pi}^\pi f(t)\sin(kt)dt\right]\sin(kx)= }[/math]
- [math]\displaystyle{ = \frac{1}{\pi}\int_{-\pi}^\pi\left[\frac{1}{2}f(t)+\sum_{k=1}^n f(t)\left(\cos(kt)\cos(kx) + \sin(kt)\sin(kx)\right)\right]dt= }[/math]
- [math]\displaystyle{ =\frac{1}{\pi}\int_{-\pi}^\pi f(t)\left[\frac{1}{2}+\sum_{k=1}^n \cos(k(t-x))\right]dt }[/math]
- זה בעצם גרעין דיריכלה, כלומר קיבלנו כי:
- [math]\displaystyle{ S_n = \frac{1}{\pi}\int_{-\pi}^\pi f(t)D_n(t-x)dt }[/math]
- שימו לב ששינוי מספר סופי של נקודות לא משפיע על האינטגרל, ולכן נקודות אי הרציפות הסליקות של גרעין דיריכלה לא פוגעות בהוכחה.
- טענה: תהי [math]\displaystyle{ f }[/math] פונקציה מחזורית [math]\displaystyle{ 2\pi }[/math]. אזי לכל [math]\displaystyle{ a\in\mathbb{R} }[/math] מתקיים כי:
- [math]\displaystyle{ \int_{-\pi}^\pi f(x)dx = \int_{-\pi+a}^{\pi+a} f(x)dx }[/math]
- כלומר, השטח מתחת לגרף הפונקציה שווה על כל קטע באורך [math]\displaystyle{ 2\pi }[/math].
- הוכחה:
- [math]\displaystyle{ \int_{-\pi+a}^{\pi+a} f(x)dx = \int_{-\pi+a}^{\pi} f(x)dx + \int_{\pi}^{\pi+a} f(x)dx }[/math]
- נבצע הצבה [math]\displaystyle{ t=x-2\pi }[/math] באינטגרל השני ונקבל:
- [math]\displaystyle{ \int_{\pi}^{\pi+a} f(x)dx = \{t=x-2\pi, dt=dx\} = \int_{-\pi}^{-\pi+a}f(t+2\pi)dt = \int_{-\pi}^{-\pi+a}f(t)dt = \int_{-\pi}^{-\pi+a}f(x)dx }[/math]
- ביחד נקבל כי:
- [math]\displaystyle{ \int_{-\pi+a}^{\pi+a} f(x)dx=\int_{-\pi+a}^{\pi} f(x)dx + \int_{-\pi}^{-\pi+a}f(x)dx = \int_{-\pi}^\pi f(x)dx }[/math]
- נחזור לסכומים החלקיים ונבצע הצבה:
- [math]\displaystyle{ S_n = \frac{1}{\pi}\int_{-\pi}^\pi f(t)D_n(t-x)dt = \{ u=t-x, du=dt\} = \frac{1}{\pi}\int_{-\pi-x}^{\pi-x} f(x+u)D_n(u)du }[/math]
- כיוון שגרעין דיריכלה ו[math]\displaystyle{ f }[/math] הן מחזוריות, נקבל:
- [math]\displaystyle{ S_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x+u)D_n(u)du=\frac{1}{\pi}\int_{-\pi}^{\pi} f(x+t)D_n(t)dt }[/math]
הרצאה 3 התכנסות נקודתית של טורי פוריה
סימונים והגדרות
- נסמן את הגבול החד צדדי מימין ב[math]\displaystyle{ f(d^+)=\lim_{x\to d^+}f(x) }[/math].
- נסמן את הגבול החד צדדי משמאל ב[math]\displaystyle{ f(d^-)=\lim_{x\to d^-}f(x) }[/math].
- שימו לב: אם הפונקציה רציפה למקוטעין, הערכים הללו תמיד מוגדרים.
- נגדיר את הנגזרת הימנית ע"י [math]\displaystyle{ f'(x^+) = \lim_{t\to 0^+}\frac{f(x+t)-f(x^+)}{t} }[/math].
- נגדיר את הנגזרת השמאלית ע"י [math]\displaystyle{ f'(x^-) = \lim_{t\to 0^-}\frac{f(x+t)-f(x^-)}{t} }[/math].
- שימו לב: ייתכן ש[math]\displaystyle{ f'(d^+)=f'(d^-) }[/math] אך הפונקציה אינה גזירה בd. זה יקרה אם היא לא רציפה בנקודה.
דוגמא:
- נביט בפונקציה [math]\displaystyle{ f(x)=\frac{x}{|x|} }[/math]
- מתקיים כי [math]\displaystyle{ f(0^+)=1 }[/math], ו[math]\displaystyle{ f(0^-)=-1 }[/math].
- כמו כן מתקיים כי [math]\displaystyle{ f'(0^+)=f'(0^-)=0 }[/math].
כמובן שהפונקציה אינה רציפה ואינה גזירה ב0.
משפט דיריכלה - התכנסות נקודתית של טור פוריה
- תהי [math]\displaystyle{ f }[/math] פונקציה מחזורית [math]\displaystyle{ 2\pi }[/math], רציפה למקוטעין כך שבכל נקודה הנגזרות החד צדדיות שלה קיימות וסופיות.
- אזי לכל [math]\displaystyle{ x\in\mathbb{R} }[/math] הטור עם מקדמי הפוריה של [math]\displaystyle{ f }[/math] מתכנס:
- [math]\displaystyle{ \frac{f(x^+)+f(x^-)}{2}=\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx) + b_n\sin(nx) }[/math]
- בפרט, בכל נקודה בה הפונקציה רציפה טור הפוריה מתכנס נקודתית לפונקציה, ובכל נקודה בה יש אי רציפות קפיצתית טור הפוריה מתכנס לממוצע הגבולות מימין ומשמאל.
הוכחה
- תהי נקודה [math]\displaystyle{ x\in\mathbb{R} }[/math].
- נביט בפונקציה [math]\displaystyle{ g(t) = \frac{f(x+t) - f(x^+)}{2\sin(\frac{t}{2})} }[/math]
- [math]\displaystyle{ \lim_{t\to 0^+}g(t) = \lim_{t\to 0^+}\frac{f(x+t) - f(x^+)}{t}\frac{\frac{t}{2}}{\sin(\frac{t}{2})} = f'(x^+)\cdot 1 }[/math]
- כיוון שהנגזרות החד צדדיות קיימות וסופיות, קיבלנו ש[math]\displaystyle{ g(t) }[/math] רציפה למקוטעין בקטע [math]\displaystyle{ [0,\pi] }[/math].
- לפי למת רימן-לבג נובע כי:
- [math]\displaystyle{ \lim_{n\to\infty}\int_0^\pi g(t)\sin\left(\left(n+\frac{1}{2}\right)t\right)dt=0 }[/math]
- כלומר:
- [math]\displaystyle{ 0=\lim_{n\to\infty}\frac{1}{\pi}\int_0^\pi \left[f(x+t)-f(x^+)\right]\frac{\sin\left(\left(n+\frac{1}{2}\right)t\right)}{2\sin(\frac{t}{2})}dt= \lim_{n\to\infty}\frac{1}{\pi}\int_0^\pi \left[f(x+t)-f(x^+)\right]D_n(t)dt }[/math]
- כיוון ש
- [math]\displaystyle{ \frac{1}{\pi}\int_0^\pi f(x^+)D_n(t)dt = \frac{f(x^+)}{2} }[/math]
- נובע כי:
- [math]\displaystyle{ \lim_{n\to\infty}\frac{1}{\pi}\int_0^\pi f(x+t)D_n(t)dt = \frac{f(x^+)}{2} }[/math]
- באופן דומה לחלוטין ניתן להוכיח כי:
- [math]\displaystyle{ \lim_{n\to\infty}\frac{1}{\pi}\int_{-\pi}^0 f(x+t)D_n(t)dt = \frac{f(x^-)}{2} }[/math]
- ולכן סה"כ נקבל כי:
- [math]\displaystyle{ \lim_{n\to\infty} S_n(x)= \lim_{n\to\infty}\frac{1}{\pi}\int_{-\pi}^{\pi} f(x+t)D_n(t)dt = \frac{f(x^-)+f(x^+)}{2} }[/math]
דוגמאות
דוגמא 1
- תהי [math]\displaystyle{ f }[/math] ההמשך המחזורי של [math]\displaystyle{ x }[/math].
- כיוון שf רציפה למקוטעין ובעלת נגזרות חד צדדיות קיימות (כולן שוות 1), תנאי משפט דיריכלה מתקיימים.
- כיוון שf הינה אי-זוגית, לכל [math]\displaystyle{ n }[/math] מתקיים כי [math]\displaystyle{ a_n=0 }[/math].
- כעת נחשב את המקדמים של הסינוסים:
- [math]\displaystyle{ b_n=\langle f,sin(nx)\rangle = \frac{1}{\pi}\int_{-\pi}^\pi x\sin(nx)dx =\frac{2}{\pi}\int_{0}^\pi x\sin(nx)dx= \frac{2}{n\pi}\left[-x\cos(nx)\right]_{0}^\pi + \frac{2}{n\pi}\int_{0}^{\pi}\cos(nx)dx = -\frac{2\pi\cos(\pi n)}{\pi n} = \frac{2(-1)^{n+1}}{n} }[/math]
- לכן, בכל נקודת רציפות של f, כלומר בכל נקודה [math]\displaystyle{ x\neq \pi +2\pi k }[/math], מתקיים כי:
- [math]\displaystyle{ f(x)=\sum_{n=1}^\infty\frac{2(-1)^{n+1}}{n}\sin(nx) }[/math].
- בפרט, לכל נקודה [math]\displaystyle{ x\in (-\pi,\pi) }[/math] מתקיים כי:
- [math]\displaystyle{ x=\sum_{n=1}^\infty\frac{2(-1)^{n+1}}{n}\sin(nx) }[/math]
- עבור נקודות אי הרציפות (הקפיצתיות), מתקיים כי הממוצע בין הגבולות החד צדדיים הוא אפס.
- קל לראות שאכן לכל [math]\displaystyle{ x=\pi+2\pi k }[/math] נקבל שטור הפורייה מתכנס לאפס (למעשה כל הסינוסים מתאפסים).
- נציב לדוגמא [math]\displaystyle{ x=\frac{\pi}{2} }[/math] ונקבל:
- [math]\displaystyle{ \frac{\pi}{2}=\sum_{n=1}^\infty\frac{2(-1)^{n+1}}{n}\sin(\frac{n\pi}{2}) }[/math]
- לכל n זוגי הסינוס יתאפס, ולכן נקבל:
- [math]\displaystyle{ \frac{\pi}{2}=\sum_{n=1}^\infty\frac{2}{2n-1}\sin(n\pi-\frac{\pi}{2}) =\sum_{n=1}^\infty\frac{-2}{2n-1}\cos(n\pi) = \sum_{n=1}^\infty\frac{2(-1)^{n+1}}{2n-1} }[/math]
- שימו לב שהפעם לא קיבלנו טור חדש בזכות פורייה, כיוון שנקבל בדיוק את אותו הטור אם נציב 1 בטור הטיילור של [math]\displaystyle{ arctan(x) }[/math].
דוגמא 2
- כעת, תהי [math]\displaystyle{ g }[/math] ההמשך המחזורי של [math]\displaystyle{ x^2 }[/math].
- הפונקציה g הינה רציפה בכל הממשיים.
- הפונקציה g גזירה בכל הממשיים פרט לנקודות [math]\displaystyle{ x=\pi+2\pi k }[/math].
- בנקודות אי הגזירות, הנגזרות החד צדדיות קיימות ושוות ל[math]\displaystyle{ \pm 2\pi }[/math] (כיוון שהנגזרת של [math]\displaystyle{ x^2 }[/math] היא [math]\displaystyle{ 2x }[/math]).
- סה"כ לפי משפט דיריכלה, טור הפוריה של g מתכנס אליה בכל הממשיים (כיוון שהיא רציפה בכל הממשיים).
- כלומר קיבלנו שלכל [math]\displaystyle{ x\in [-\pi,\pi] }[/math] מתקיים כי:
- [math]\displaystyle{ x^2=\frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4(-1)^n}{n^2}cos(nx) }[/math]
- שימו לב שאם נגזור איבר איבר את טור הפוריה של [math]\displaystyle{ x^2 }[/math], נקבל את טור הפורייה של [math]\displaystyle{ 2x }[/math].
- האם זה מפתיע?
דוגמא 3
- תהי [math]\displaystyle{ h }[/math] ההמשך המחזורי של הפונקציה [math]\displaystyle{ \begin{cases}x & x\in [0,\pi]\\0 & x\in [-\pi,0)\end{cases} }[/math]
- שוב, קיבלנו פונקציה רציפה למקוטעין עם נגזרות חד צדדיות קיימות וסופיות.
- נחשב את מקדמי הפורייה:
- [math]\displaystyle{ a_0=\frac{1}{\pi}\int_0^\pi xdx = \frac{\pi}{2} }[/math]
- [math]\displaystyle{ a_n = \frac{1}{\pi}\int_0^\pi x\cos(nx)dx = \frac{1}{n\pi}\left[x\sin(nx)\right]_0^\pi - \frac{1}{n\pi}\int_0^\pi \sin(nx)dx = \frac{1}{n^2\pi}\left[\cos(nx)\right]_0^\pi= \frac{(-1)^n-1}{\pi n^2} }[/math]
- [math]\displaystyle{ b_n = \frac{1}{\pi}\int_0^\pi x\sin(nx)dx = \frac{-1}{n\pi}\left[x\cos(nx)\right]_0^\pi + \frac{1}{n\pi}\int_0^\pi \cos(nx)dx = \frac{(-1)^{n+1}}{n} }[/math]
- סה"כ שלכל [math]\displaystyle{ x\in (-\pi,\pi) }[/math] מתקיים כי:
- [math]\displaystyle{ h(x) = \frac{\pi}{4} + \sum_{n=1}^\infty \left[\frac{(-1)^n-1}{\pi n^2}\cos(nx) + \frac{(-1)^{n+1}}{n}\sin(nx)\right] }[/math]
- שימו לב: מצאנו שני טורי פורייה שמתכנסים ל[math]\displaystyle{ x }[/math] בקטע [math]\displaystyle{ (0,\pi) }[/math].
- באופן דומה אפשר להראות שקיימים אינסוף טורי פורייה כאלה.
טור הנגזרת
- תהי [math]\displaystyle{ f }[/math] רציפה בקטע [math]\displaystyle{ [-\pi,\pi] }[/math] כך שהנגזרת שלה [math]\displaystyle{ f' }[/math] רציפה למקוטעין בקטע.
שימוש בנוסחאת ניוטון לייבניץ לחישוב האינטגרל המסויים
- שימו לב שמותר לנו להשתמש בנוסחאת ניוטון לייבניץ:
- כיוון שהנגזרת רציפה למקוטעין, אפשר להראות בעזרת לופיטל שהנגזרות החד צדדיות בנקודות אי הגזירות של f קיימות.
- בעצם, זה מראה שf גזירה בקטעים סגורים בהם אפשר להפעיל את נוסחאת ניוטון לייבניץ.
- אם נחשב את האינטגרל על הנגזרת בכל הקטעים הסגורים, ערכי f יצטמצמו, פרט לקצוות.
- לדוגמא:
- [math]\displaystyle{ \int_{-1}^1 \frac{x}{|x|}dx = \int_{-1}^0 (-1)dx + \int_{0}^1 (1)dx = (-x)|_{-1}^0+(x)|_0^1 = 0-1 + 1-0 = 1-1 }[/math]
- כלומר קיבלנו כי [math]\displaystyle{ \int_{-1}^1 \frac{x}{|x|}dx = (|x|)_{-1}^{1} }[/math], כאשר [math]\displaystyle{ (|x|)' = \frac{x}{|x|} }[/math]
חישוב מקדמי טור הפורייה של הנגזרת
- נסמן את מקדמי הפורייה של [math]\displaystyle{ f }[/math] ב[math]\displaystyle{ a_n,b_n }[/math]
- נחשב את מקדמי הפורייה של הנגזרת, נסמן אותם ב[math]\displaystyle{ \alpha_n,\beta_n }[/math]:
- [math]\displaystyle{ \alpha_0=\frac{1}{\pi}\int_{-\pi}^{\pi}f'(x)dx= \frac{f(\pi)-f(-\pi)}{\pi} }[/math]
- [math]\displaystyle{ \alpha_n=\frac{1}{\pi} \int_{-\pi}^\pi f'(x)\cos(nx)dx = \frac{1}{\pi}\left[f(x)\cos(nx)\right]_{-\pi}^\pi +\frac{n}{\pi}\int_{-\pi}^\pi f(x)\sin(nx)dx = \frac{(-1)^n\left(f(\pi)-f(-\pi)\right)}{\pi}+n\cdot b_n = (-1)^n\alpha_0+nb_n }[/math]
- [math]\displaystyle{ \beta_n=\frac{1}{\pi} \int_{-\pi}^\pi f'(x)\sin(nx)dx = \frac{1}{\pi}\left[f(x)\sin(nx)\right]_{-\pi}^\pi -\frac{n}{\pi}\int_{-\pi}^\pi f(x)\cos(nx)dx = -n\cdot a_n }[/math]
- כלומר, בתנאים הנתונים, אם טור הפוריה של f הינו:
- [math]\displaystyle{ f(x)\sim\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx) }[/math]
- אזי טור הפורייה של הנגזרת הינו:
- [math]\displaystyle{ f'(x)\sim\frac{\alpha_0}{2}+\sum_{n=1}^\infty \left((-1)^n\alpha_0+nb_n\right)\cos(nx)-n\cdot a_n\sin(nx) }[/math]
- במקרה המיוחד בו [math]\displaystyle{ f(-\pi)=f(\pi) }[/math] מתקיים כי [math]\displaystyle{ \alpha_0=0 }[/math] ולכן נקבל את טור הפורייה הפשוט:
- [math]\displaystyle{ f'(x)\sim\sum_{n=1}^\infty nb_n\cos(nx)-na_n\sin(nx) }[/math]
דוגמאות
דוגמא 1
- נזכר בטור הפורייה של [math]\displaystyle{ x^2 }[/math]:
- [math]\displaystyle{ \frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4(-1)^n}{n^2}cos(nx) }[/math]
- נרצה למצוא את מקדמי הפוריה של [math]\displaystyle{ \frac{x^3}{3} }[/math], נסמנם ב[math]\displaystyle{ a_n,b_n }[/math].
- לכל [math]\displaystyle{ 1\leq n }[/math] נקבל כי:
- [math]\displaystyle{ \frac{2(-1)^n\pi^2}{3}+nb_n = \frac{4(-1)^n}{n^2} }[/math]
- [math]\displaystyle{ -na_n = 0 }[/math]
- כמו כן נחשב את המקדם הראשון:
- [math]\displaystyle{ a_0=\frac{1}{\pi}\int_{-\pi}^\pi \frac{x^3}{3}dx = 0 }[/math]
- נחלץ את המקדמים ונקבל כי טור הפורייה של [math]\displaystyle{ \frac{x^3}{3} }[/math] הוא:
- [math]\displaystyle{ \frac{x^3}{3} \sim \sum_{n=1}^\infty \frac{2(-1)^n}{n^3}\left(2-\frac{\pi^2 n^2}{3}\right)\sin(nx) }[/math]
דוגמא 2
- נחשב את טור הפורייה של [math]\displaystyle{ e^x }[/math].
- נסמן את טור הפורייה של [math]\displaystyle{ e^x }[/math] ב:
- [math]\displaystyle{ \frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx) }[/math]
- כמובן שהנגזרת במקרה הזה שווה לפונקציה, ולכן יש לה בדיוק אותו טור פורייה.
- מצד שני, טור הפורייה של הנגזרת צריך להיות:
- [math]\displaystyle{ \frac{\alpha_0}{2}+\sum_{n=1}^\infty \left((-1)^n\alpha_0+nb_n\right)\cos(nx) -na_n\sin(nx) }[/math]
- כאשר [math]\displaystyle{ \alpha_0=\frac{f(\pi)-f(-\pi)}{\pi}=\frac{e^\pi-e^{-\pi}}{\pi} }[/math]
- ביחד נקבל את המשוואות:
- [math]\displaystyle{ a_0=\alpha_0 }[/math]
- [math]\displaystyle{ a_n=(-1)^n\alpha_0+nb_n }[/math]
- [math]\displaystyle{ b_n=-na_n }[/math]
- נציב את המשוואה השלישית בשנייה ונקבל:
- [math]\displaystyle{ a_n=\frac{(-1)^n\alpha_0}{1+n^2} }[/math]
- ולכן
- [math]\displaystyle{ b_n=\frac{n(-1)^{n+1}\alpha_0}{1+n^2} }[/math]
- סה"כ קיבלנו כי טור הפורייה של [math]\displaystyle{ e^x }[/math] הינו:
- [math]\displaystyle{ \frac{\alpha_0}{2}+\sum_{n=1}^\infty \frac{(-1)^n\alpha_0}{1+n^2}\cos(nx) + \frac{n(-1)^{n+1}\alpha_0}{1+n^2}\sin(nx) }[/math]
- כיוון שלהמשך המחזורי של [math]\displaystyle{ e^x }[/math] יש אי רציפות קפיצתית ב[math]\displaystyle{ x=\pi }[/math], טור הפורייה שם מתכנס לממוצע [math]\displaystyle{ \frac{e^\pi+e^{-\pi}}{2} }[/math]
- כלומר, אם נציב [math]\displaystyle{ x=\pi }[/math] נקבל:
- [math]\displaystyle{ \frac{1}{\alpha_0}\frac{e^\pi+e^{-\pi}}{2} = \frac{1}{2} +\sum_{n=1}^\infty \frac{1}{1+n^2} }[/math]
- נפשט:
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{1}{1+n^2}=\frac{\pi(e^\pi+e^{-\pi})}{2(e^\pi-e^{-\pi})}-\frac{1}{2} }[/math]
הרצאה 4 - התכנסות במ"ש ושיוויון פרסבל
תנאי להתכנסות במ"ש של טור פורייה
- תהי [math]\displaystyle{ f }[/math] רציפה בקטע [math]\displaystyle{ [-\pi,\pi] }[/math] המקיימת [math]\displaystyle{ f(-\pi)=f(\pi) }[/math], כך ש [math]\displaystyle{ f' }[/math] רציפה למקוטעין.
- אזי טור הפורייה של [math]\displaystyle{ f }[/math] מתכנס אליה במ"ש בכל הממשיים.
- לפי משפט דיריכלה ידוע כי טור הפורייה של ההמשך המחזורי של f מתכנס אליה בכל נקודה.
- נסמן את טור הפורייה ב
- [math]\displaystyle{ \frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx) }[/math]
- ברור כי
- [math]\displaystyle{ \left|\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx)\right|\leq \frac{|a_0|}{2} + \sum_{n=1}^\infty |a_n|+|b_n| }[/math]
- לפי מבחן ה-M של ויירשטראס, מספיק להוכיח שטור המספרים מימין מתכנס על מנת להסיק שטור הפורייה מתכנס במ"ש.
- נסמן את מקדמי פורייה של הנגזרת ב[math]\displaystyle{ \alpha_n,\beta_n }[/math].
- כבר חישבנו ש:
- [math]\displaystyle{ \alpha_0=0 }[/math]
- [math]\displaystyle{ \alpha_n=nb_n }[/math]
- [math]\displaystyle{ \beta_n=-na_n }[/math]
- לכן ביחד נקבל כי [math]\displaystyle{ \sqrt{|a_n|^2+|b_n|^2}=\frac{1}{n}\sqrt{|\alpha_n|^2+|\beta_n|^2} }[/math]
- לפי אי שיוויון קושי שוורץ, נקבל כי לכל n מתקיים:
- [math]\displaystyle{ \sum_{n=1}^N \frac{\sqrt{|\alpha_n|^2+|\beta_n|^2}}{n} \leq \sqrt{\sum_{n=1}^N\frac{1}{n^2}}\sqrt{\sum_{n=1}^N |\alpha_n|^2+|\beta_n|^2} }[/math]
- לפי אי שיוויון בסל, אנו יודעים כי הטור [math]\displaystyle{ \sum_{n=1}^\infty |\alpha_n|^2+|\beta_n|^2 }[/math] מתכנס, כיוון שמדובר במקדמי פורייה של [math]\displaystyle{ f'\in E }[/math].
- (זכרו שמותר להניח כי [math]\displaystyle{ f'\in E }[/math] על ידי שינוי מספר סופי של נקודות שלא משפיעות על חישוב מקדמי הפורייה.)
- לכן [math]\displaystyle{ \left(\sum_{n=1}^N\frac{1}{n^2}\right),\left(\sum_{n=1}^N |\alpha_n|^2+|\beta_n|^2\right) }[/math] חסומות כסדרות סכומים חלקיים של טורים מתכנסים.
- לכן סה"כ [math]\displaystyle{ \sum_{n=1}^N \frac{\sqrt{|\alpha_n|^2+|\beta_n|^2}}{n} }[/math] חסומה, ולכן הטור האינסופי המתאים לה מתכנס.
- סה"כ קיבלנו כי [math]\displaystyle{ \sum_{n=1}^\infty \sqrt{|a_n|^2+|b_n|^2} }[/math] מתכנס.
- לכן בוודאי גם הטורים הקטנים יותר [math]\displaystyle{ \sum_{n=1}^\infty |a_n| }[/math] ו[math]\displaystyle{ \sum_{n=1}^\infty |b_n| }[/math] מתכנסים, כפי שרצינו.
שיוויון פרסבל
- נביט במערכת האורתונורמלית [math]\displaystyle{ \{\frac{1}{\sqrt{2}},\cos(x),\sin(x),\cos(2x),\sin(2x),...\}\subseteq E }[/math], ותהי [math]\displaystyle{ f\in E }[/math].
- ידוע לנו כי [math]\displaystyle{ a_0=\langle f,1\rangle }[/math], ולכן [math]\displaystyle{ \frac{a_0}{\sqrt{2}}=\langle f,\frac{1}{\sqrt{2}}\rangle }[/math]
- נסמן את סדרת הסכומים החלקיים של טור הפורייה המתאים לפונקציה f ב [math]\displaystyle{ S_n }[/math].
- [math]\displaystyle{ S_n }[/math] היא ההיטל של [math]\displaystyle{ f }[/math] על הקבוצה האורתונורמלית [math]\displaystyle{ \{\frac{1}{\sqrt{2}},\cos(x),\sin(x),\cos(2x),\sin(2x),...,\cos(nx),\sin(nx)\} }[/math]
- אכן [math]\displaystyle{ \langle f,\frac{1}{\sqrt{2}}\rangle \frac{1}{\sqrt{2}} + \sum_{n=1}^\infty \langle f,\cos(nx)\rangle \cos(nx) + \langle f,\sin(nx)\rangle \sin(nx) = \frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx) }[/math]
- נזכור כי [math]\displaystyle{ ||v||^2=||v-\widetilde{v}||^2+||\widetilde{v}||^2 }[/math]
- לכן [math]\displaystyle{ ||f-S_n||^2=||f||^2-||S_n||^2 }[/math].
- כמו כן, נזכור כי [math]\displaystyle{ ||\widetilde{v}||^2 = \sum_{i=1}^{n}|\langle v,e_i\rangle|^2 }[/math]
- לכן [math]\displaystyle{ ||S_n||^2 = \frac{|a_0|^2}{2}+\sum_{k=1}^n |a_k|^2+|b_k|^2 }[/math]
- אי שיוויון בסל אומר כי [math]\displaystyle{ \sum_{i=1}^\infty |\langle v,e_i\rangle|^2 \leq ||v||^2 }[/math]
- כלומר:
- [math]\displaystyle{ \frac{|a_0|^2}{2}+\sum_{n=1}^\infty |a_n|^2+|b_n|^2 \leq ||f||^2 = \langle f,f\rangle = \frac{1}{\pi}\int_{-\pi}^{\pi} |f(x)|^2dx }[/math]
- משפט שיוויון פרסבל אומר שבעצם מתקיים שיוויון:
- [math]\displaystyle{ \frac{1}{\pi}\int_{-\pi}^{\pi} |f(x)|^2dx=\frac{|a_0|^2}{2}+\sum_{n=1}^\infty |a_n|^2+|b_n|^2 }[/math]
- אם נוכיח ש [math]\displaystyle{ ||f-S_n||^2\to 0 }[/math], נסיק כי [math]\displaystyle{ ||S_n||^2\to ||f||^2 }[/math] וזהו בדיוק שיוויון פרסבל.
הוכחת שיוויון פרסבל כאשר טור הפורייה מתכנס במ"ש
- תהי [math]\displaystyle{ f }[/math] רציפה בקטע [math]\displaystyle{ [-\pi,\pi] }[/math] המקיימת [math]\displaystyle{ f(-\pi)=f(\pi) }[/math], כך שהנגזרת שלה [math]\displaystyle{ f' }[/math] רציפה למקוטעין.
- נסמן [math]\displaystyle{ d_n=\sup_{[-\pi,\pi]}|f-S_n| }[/math]
- הוכחנו כי טור הפורייה של f מתכנס אליה במ"ש, כלומר [math]\displaystyle{ d_n\to 0 }[/math].
- לכן [math]\displaystyle{ ||f-S_n||^2 = \frac{1}{\pi}\int_{-\pi}^{\pi} |f-S_n|^2dx \leq 2d_n^2 \to 0 }[/math]
דוגמא
- הפונקציה [math]\displaystyle{ f(x)=x^2 }[/math] מקיימת את דרישות המשפט.
- נזכור כי טור הפורייה שלה הוא:
- [math]\displaystyle{ \frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4(-1)^n}{n^2}cos(nx) }[/math]
- לכן לפי שיוויון פרסבל נקבל כי:
- [math]\displaystyle{ \frac{1}{\pi}\int_{-\pi}^{\pi} x^4dx = \frac{4\pi^4}{18}+\sum_{n=1}^\infty \frac{16}{n^4} }[/math]
- [math]\displaystyle{ \frac{2\pi^4}{5}-\frac{4\pi^4}{18} = \sum_{n=1}^\infty \frac{16}{n^4} }[/math]
- ולכן:
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{1}{n^4} = \frac{\pi^4}{90} }[/math]
הוכחת שיוויון פרסבל במקרה הכללי
- תהי [math]\displaystyle{ f \in E }[/math], אנחנו מעוניינים להוכיח כי [math]\displaystyle{ ||f-S_m||\to 0 }[/math].
- נבנה סדרת פונקציות [math]\displaystyle{ f_n }[/math] רציפות בקטע [math]\displaystyle{ [-\pi,\pi] }[/math] המקיימות [math]\displaystyle{ f_n(-\pi)=f_n(\pi) }[/math], כך שהנגזרות שלהן [math]\displaystyle{ f_n' }[/math] רציפות למקוטעין, המקיימות:
- [math]\displaystyle{ ||f-f_n||\to 0 }[/math]
- יהי [math]\displaystyle{ \varepsilon }[/math], נבחר [math]\displaystyle{ n }[/math] כך ש [math]\displaystyle{ ||f-f_n||\lt \frac{\varepsilon}{2} }[/math].
- נסמן ב[math]\displaystyle{ T_m }[/math] את סדרת הסכומים החלקיים של טור הפורייה של [math]\displaystyle{ f_n }[/math].
- ראינו כי [math]\displaystyle{ \lim_{m\to\infty}||f_n-T_m||=0 }[/math].
- כיוון שההיטל הוא הוקטור הקרוב ביותר, נקבל:
- [math]\displaystyle{ ||f-S_m||\leq ||f-T_m|| }[/math]
- כמו כן, [math]\displaystyle{ ||f-T_m||\leq ||f-f_n||+||f_n-T_m|| }[/math]
- קיים מקום החל ממנו לכל [math]\displaystyle{ m }[/math] מתקיים כי [math]\displaystyle{ ||f_n-T_m||\lt \frac{\varepsilon}{2} }[/math].
- לכן החל ממקום זה [math]\displaystyle{ ||f-S_m||\lt \varepsilon }[/math] כפי שרצינו.
בניית סדרת הפונקציות
- f רציפה למקוטעין, ולכן רציפה במ"ש בכל קטע רציפות.
- לכן ניתן לבחור חלוקה [math]\displaystyle{ P }[/math] הכוללת את נקודות אי הרציפות, עם פרמטר חלוקה מספיק קטן כך ש [math]\displaystyle{ |f(x)-f(c_k)|^2\lt \frac{\varepsilon}{2\pi} }[/math] לכל זוג נקודות [math]\displaystyle{ x,c_k\in [x_{k-1},x_k] }[/math].
- נבחר נקודות כלשהן [math]\displaystyle{ c_k }[/math] בכל קטע ונביט בפונקצית המדרגות g שבכל תת קטע שווה לקבוע [math]\displaystyle{ f(c_k) }[/math].
- כעת האינטגרל תמיד קטן מסכום הדרבו העליון:
- [math]\displaystyle{ \int_{-\pi}^{\pi} |f-g|^2dx \leq \sum_{k=1}^n \sup_{[x_{k-1},x_k]}|f(x)-f(c_k)|^2 (x_k-x_{k-1}) \leq \sum_{k=1}^n \frac{\varepsilon}{2\pi}(x_k-x_{k-1}) = \varepsilon }[/math]
- לכן אפשר לבנות סדרת פונקציות מדרגות כנ"ל [math]\displaystyle{ g_n }[/math] כך ש[math]\displaystyle{ ||f-g_n||\lt \frac{1}{n} }[/math]
- כעת נגדיר סדרת פונקציות [math]\displaystyle{ f_n }[/math] להיות [math]\displaystyle{ g_n }[/math], פרט לשינויים הבאים:
- עבור [math]\displaystyle{ \delta }[/math] שנקבע בהמשך, נחבר בקו ישר את הנקודות בקצוות המקטעים [math]\displaystyle{ [x_k-\delta,x_k] }[/math].
- נגדיר [math]\displaystyle{ f_n(-\pi)=g(\pi) }[/math].
- נחבר בקו ישר את הנקודות בקצה הקטע [math]\displaystyle{ [x_0,x_0+\delta] }[/math].
- עבור [math]\displaystyle{ \delta }[/math] קטנה מספיק, [math]\displaystyle{ \int_{-\pi}^{\pi}|f_n-g|^2dx \lt \frac{1}{n} }[/math].
- סה"כ נקבל כי
- [math]\displaystyle{ f_n }[/math] מורכבת מקטעים ישרים המחוברים זה לזה, ולכן מדובר בפונקציה רציפה, בעלת נגזרת רציפה למקוטעין.
- [math]\displaystyle{ f_n(-\pi)=f_n(\pi) }[/math]
- אכן מתקיים כי [math]\displaystyle{ ||f-f_n||\leq ||f-g||+||g-f_n||\to 0 }[/math]
יחידות טור פורייה
הם ישנן שתי פונקציות שונות בעלות אותו טור פורייה?
- תהיינה [math]\displaystyle{ f,g\in E }[/math] בעלות אותם מקדמי פורייה.
- אם טורי הפורייה מתכנסים לפונקציה, ברור שזו אותה הפונקציה, אבל אם לא?
- מקדמי הפורייה של [math]\displaystyle{ f-g }[/math] הם אפס, ולכן לפי שיוויון פרסבל:
- [math]\displaystyle{ ||f-g||^2=0 }[/math]
- לכן [math]\displaystyle{ f=g }[/math].
- שימו לב שעבור סתם פונקציות רציפות למקוטעין, זה אומר ש[math]\displaystyle{ f=g }[/math] פרט למספר סופי של נקודות.
האם תתכן פונקציה אחת, בעלת שני טורים טריגונומטריים?
- קנטור הוכיח שאם טור טריגונומטרי שווה לאפס בכל הקטע [math]\displaystyle{ [-\pi,\pi] }[/math], אזי כל מקדמי הטור הם אפס.
- יותר מאוחר הוכיחו כי אם הטור מתאפס בכל נקודה בקטע פרט לקבוצה בת מנייה של נקודות, עדיין כל מקדמי הטור הם אפס.
- מנשוב מצא ב1916 טור טריגונומטרי שמתכנס לאפס בכל נקודה פרט לקבוצה ממידה אפס של נקודות, אך לא כל מקדמי הטור הם אפס.
הרצאה 5 - תופעת גיבס, טורי הסינוסים והקוסינוסים
תופעת גיבס
- ראינו תנאים בהם טור הפורייה מתכנס במ"ש.
- כעת אנחנו רוצים לחקור מקרים בהם אין התכנסות במ"ש, ונראה כי בהן יש חריגה מיוחדת של סדרת הסכומי החלקיים מן הפונקציה.
- נביט בטור פורייה של הפונקציה x:
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{2(-1)^{n+1}}{n}\sin(nx) }[/math]
- נסמן ב[math]\displaystyle{ S_m }[/math] את סדרת הסכומים החלקיים של הטור ונביט ב:
- [math]\displaystyle{ S_m(\pi - \frac{\pi}{m})=\sum_{n=1}^m \frac{2(-1)^{n+1}}{n}\sin(n(\pi - \frac{\pi}{m})) = \sum_{n=1}^m \frac{2}{n}\sin(\frac{n\pi}{m}) }[/math]
- כעת,
- [math]\displaystyle{ \sum_{n=1}^m \frac{2}{n}\sin(\frac{n\pi}{m}) = 2\sum_{n=1}^m \frac{\sin\left(\frac{n\pi}{m}\right)}{\left(\frac{n\pi}{m}\right)}\frac{\pi}{m}\to 2\int_0^\pi \frac{\sin(x)}{x}dx }[/math]
- לכן סה"כ השגיאה בקירוב ע"י הסכומים החלקיים בסדרת הנקודות הללו היא:
- [math]\displaystyle{ \pi-\frac{\pi}{m} - S_m (\pi-\frac{\pi}{m}) \to \pi - 2\int_0^\pi \frac{\sin(x)}{x}dx = \int_0^\pi (1-\frac{2\sin(x)}{x})dx \approx -0.56 }[/math]
- (הערכת האינטגרל נעשית על ידי פיתוח טור הטיילור של הפונקציה, נקבל טור לייבניץ לפיו קל לבצע הערכת שגיאה.)
- כלומר סדרת הסכומים החלקיים עולה משמעותית מעל הפונקציה, כפי שניתן לראות בגרף המצורף.
- אם נחלק את זה בגודל הקפיצה בין הגבולות החד צדדים של ההמשך המחזורי של x בנקודה [math]\displaystyle{ \pi }[/math], נקבל בערך [math]\displaystyle{ -0.089 }[/math].
- לא נוכיח זאת, אבל יחס הטעות הזה בנקודות אי הרציפות נשמר באופן כללי עבור פונקציות בE שנגזרתן רציפה למקוטעין, ונקרא 'תופעת גיבס'.
טור הסינוסים וטור הקוסינוסים
- עבור פונקציה [math]\displaystyle{ f }[/math] הרציפה בקטע [math]\displaystyle{ [0,\pi] }[/math] ובעלת נגזרת רציפה למקוטעין, ניתן להשלים אותה לפונקציה [math]\displaystyle{ f^+ }[/math] הזוגית בקטע [math]\displaystyle{ [-\pi,\pi] }[/math], או ל[math]\displaystyle{ f^- }[/math] האי זוגית בקטע [math]\displaystyle{ [-\pi,\pi] }[/math].
- את ההמשך הזוגי אפשר לפתח לטור קוסינוסים, שמתכנס במ"ש בקטע [math]\displaystyle{ [0,\pi] }[/math]. זה נקרא טור הקוסינוסים של הפונקציה [math]\displaystyle{ f }[/math].
- הוכחה:
- [math]\displaystyle{ f^+ }[/math] רציפה ב[math]\displaystyle{ [-\pi,\pi] }[/math], בעלת נגזרת רציפה למקוטעין, ומתקיים כמובן ש[math]\displaystyle{ f(-\pi)=f(\pi) }[/math].
- את ההמשך האי זוגי אפשר לפתח לטור סינוסים, שמתכנס אל הפונקציה בקטע [math]\displaystyle{ (0,\pi) }[/math]. זה נקרא טור הסינוסים של הפונקציה [math]\displaystyle{ f }[/math].
- אם [math]\displaystyle{ f(\pi)=f(0)=0 }[/math] אזי טור הסינוסים מתכנס במ"ש בקטע [math]\displaystyle{ [0,\pi] }[/math].
- הוכחה:
- [math]\displaystyle{ f^- }[/math] רציפה כיוון ש[math]\displaystyle{ f(0)=0 }[/math], ומתקיים כי [math]\displaystyle{ f(-\pi)=-f(\pi)=0=f(\pi) }[/math].
- חישוב המקדמים:
- עבור טור הקוסינוסים:
- [math]\displaystyle{ a_n=\frac{1}{\pi}\int_{-\pi}^{\pi} f^+\cos(nx) dx = \frac{2}{\pi}\int_{0}^{\pi}f\cos(nx)dx }[/math]
- עבור טור הסינוסים:
- [math]\displaystyle{ b_n=\frac{1}{\pi}\int_{-\pi}^{\pi} f^-\cos(nx) dx = \frac{2}{\pi}\int_{0}^{\pi}f\sin(nx)dx }[/math]
דוגמאות
- נחשב טור קוסינוסים של [math]\displaystyle{ e^x }[/math]:
- [math]\displaystyle{ a_0 = \frac{2}{\pi}\int_0^{\pi} e^xdx = \frac{2}{\pi}(e^\pi-1) }[/math]
- [math]\displaystyle{ a_n = \frac{2}{\pi}\int_0^{\pi} e^x\cos(nx)dx = \frac{2}{\pi}\frac{e^\pi(-1)^n-1}{n^2+1} }[/math]
- הטור מתכנס במ"ש לפונקציה בקטע [math]\displaystyle{ [0,\pi] }[/math]:
- [math]\displaystyle{ e^x=\frac{e^\pi-1}{\pi}+ \frac{2}{\pi}\sum_{n=1}^\infty \frac{e^\pi(-1)^n-1}{n^2+1}\cos(nx) }[/math]
- לכן מותר לבצע אינטגרציה איבר איבר, נחשב את [math]\displaystyle{ \int_0^x }[/math] בשני הצדדים ונקבל:
- [math]\displaystyle{ e^x-1 - \frac{e^\pi-1}{\pi}x = \frac{2}{\pi}\sum_{n=1}^\infty \frac{e^\pi(-1)^n-1}{n^3+n}\sin(nx) }[/math]
- נציב למשל [math]\displaystyle{ x=0 }[/math] ונקבל את השיוויון:
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{e^\pi(-1)^n-1}{n^2+1} = \frac{\pi}{2} - \frac{e^\pi-1}{2} }[/math]
- נחשב טור סינוסים של [math]\displaystyle{ e^x }[/math]:
- [math]\displaystyle{ b_n=\frac{2}{\pi}\int_0^\pi e^x\sin(nx)dx = \frac{2n(1-e^\pi(-1)^n)}{\pi(n^2+1)} }[/math]
- הטור מתכנס בקטע [math]\displaystyle{ (0,\pi) }[/math]:
- [math]\displaystyle{ e^x=\sum_{n=1}^\infty \frac{2n(1-e^\pi(-1)^n)}{\pi(n^2+1)}\sin(nx) }[/math]
- נחשב טור סינוסים של [math]\displaystyle{ f(x)=\pi x - x^2 }[/math].
- שימו לב: [math]\displaystyle{ f(0)=f(\pi)=0 }[/math].
- [math]\displaystyle{ b_n=\frac{2}{\pi}\int_0^\pi (\pi x-x^2)\sin(nx)dx = \frac{4(1-(-1)^n)}{\pi n^3} }[/math]
- לכן הטור מתכנס במ"ש בקטע [math]\displaystyle{ [0,\pi] }[/math]:
- [math]\displaystyle{ \pi x - x^2 = \sum_{n=1}^\infty \frac{4(1-(-1)^n)}{\pi n^3} \sin(nx) }[/math]
- לכן מותר לבצע אינטגרציה איבר איבר, נחשב את [math]\displaystyle{ \int_0^x }[/math] בשני הצדדים ונקבל:
- [math]\displaystyle{ \frac{\pi x^2}{2} - \frac{x^3}{3} = \sum_{n=1}^\infty \frac{4(1-(-1)^n)}{\pi n^4}(-\cos(nx)+1) }[/math]
- שימו לב שלא מדובר בטור טריגונומטרי.
הרצאה 6 - משוואת החום על טבעת, התמרת פורייה
משוואת החום על טבעת
- נביט במד"ח החום על מוט עבור הפונקציה [math]\displaystyle{ u(x,t) }[/math]:
- [math]\displaystyle{ u_t-ku_{xx}=0 }[/math]
- [math]\displaystyle{ u(x,0)=f(x) }[/math] (תנאי התחלה)
- [math]\displaystyle{ u(-\pi,t)=u(\pi,t) }[/math] (תנאי שפה)
- [math]\displaystyle{ u_x(-\pi,t)=u_x(\pi,t) }[/math] (תנאי שפה)
- כאשר [math]\displaystyle{ x\in[-\pi,\pi] }[/math], ו[math]\displaystyle{ t\in[0,\infty) }[/math]
- על מנת להבין את תנאי השפה, אפשר לחשוב על הבעייה במובן שהמוט הוא מעגלי.
- נחפש פתרון מהצורה [math]\displaystyle{ u(x,t)=X(x)\cdot T(t) }[/math].
- נציב במד"ח את הניחוש, ונקבל:
- [math]\displaystyle{ X(x)T'(t)=kX''(x)T(t) }[/math]
- נניח שהצדדים שונים מאפס ונחלק:
- [math]\displaystyle{ \frac{T'(t)}{kT(t)}=\frac{X''(x)}{X(x)} }[/math]
- כיוון שכל צד תלוי במשתנה אחר, הדרך היחידה לקבל שיוויון היא אם שני הצדדים קבועים.
- נביט בפתרונות עבור קבוע שלילי:
- [math]\displaystyle{ \frac{T'(t)}{kT(t)}=\frac{X''(x)}{X(x)}=-\lambda }[/math]
- כעת נפתור את המד"רים בנפרד:
- שימו לב שאנו בוחרים את השמות של הקבועים בצורה מיוחדת לקראת הפתרון בהמשך.
- עבור [math]\displaystyle{ \lambda=0 }[/math]:
- [math]\displaystyle{ X_0(x)=cx+\frac{a_0}{2} }[/math], ועל מנת לקיים את תנאי השפה נקבל כי [math]\displaystyle{ c=0 }[/math]
- [math]\displaystyle{ T_0(t)=1 }[/math] (הקבוע יבלע בקבוע של [math]\displaystyle{ X_0(x) }[/math])
- עבור [math]\displaystyle{ \lambda=0 }[/math]:
- עבור [math]\displaystyle{ \lambda\neq 0 }[/math]:
- [math]\displaystyle{ X= a_{\sqrt{\lambda}} \cos(\sqrt{\lambda}x) + b_{\sqrt{\lambda}} \sin(\sqrt{\lambda}x) }[/math]
- [math]\displaystyle{ T=e^{-k\lambda t} }[/math] (הקבוע חסר כי הוא יבלע בקבועים האחרים כאשר נכפול ב[math]\displaystyle{ X(x) }[/math])
- עבור [math]\displaystyle{ \lambda\neq 0 }[/math]:
- ע"י הצבה ניתן לוודא שעבור [math]\displaystyle{ \lambda=n^2 }[/math] הפונקציות לעיל מקיימות את תנאי השפה.
- גם צירוף לינארי שלהן יהווה פתרון כיוון שהמד"ח הומוגנית ותנאי השפה הומוגניים.
- צירוף לינארי אינסופי יהווה פתרון לבעייה אם טורי הנגזרות יתכנסו במ"ש (ולכן יהיה מותר לגזור איבר איבר).
- לכן אנו מחפשים פתרון כללי מהצורה:
- [math]\displaystyle{ u(x,t)=T_0(t)X_0(x)+\sum_{n=1}^\infty T_n(t)X_n(x) = \frac{a_0}{2} + \sum_{n=1}^\infty e^{-kn^2 t}(a_n\cos(nx)+b_n\sin(nx)) }[/math]
- כל שנותר לנו לעשות הוא למצוא את הקבועים [math]\displaystyle{ a_n,b_n }[/math].
- נציב כעת בתנאי ההתחלה [math]\displaystyle{ u(x,0)=f(x) }[/math] ונקבל בעצם את טור הפורייה:
- [math]\displaystyle{ f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(nx)+b_n\sin(nx) }[/math]
- אנחנו יכולים לפתור משוואה זו בהנתן שf מקיימת את תנאי משפט דיריכלה.
- מדוע זה יהיה פתרון?
- נזכור שמקדמי הפורייה שואפים לאפס.
- בזכות האקספוננט, טור זה ונגזרותיו אכן יתכנסו במ"ש עבור [math]\displaystyle{ t\in [a,\infty) }[/math] לכל [math]\displaystyle{ a\gt 0 }[/math] ולכל [math]\displaystyle{ x\in[-\pi,\pi] }[/math].
- לכן מותר לגזור איבר איבר, ואכן מדובר בפתרון של המד"ח.
התמרת פורייה
טור פורייה המרוכב
- לא קשה לוודא כי [math]\displaystyle{ \{e^{inx}\}_{n\in\mathbb{Z}} }[/math] מהווה קבוצה אורתונורמלית בE אם נעדכן מעט את המכפלה הפנימית:
- [math]\displaystyle{ \langle f,g\rangle = \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)\overline{g(x)}dx }[/math]
- תהי [math]\displaystyle{ f\in E }[/math], שאלה שעולה באופן טבעי היא האם:
- [math]\displaystyle{ f=\sum_{n=-\infty}^\infty \langle f,e^{inx}\rangle e^{inx} }[/math]
- כאשר אנו מגדירים את הסכום ממינוס אינסוף עד אינסוף באופן הבא:
- [math]\displaystyle{ \sum_{n=-\infty}^\infty u_n = u_0+\sum_{n=1}^\infty (u_n+u_{-n}) }[/math]
- נסמן את מקדמי פורייה הרגילים ב[math]\displaystyle{ a_n,b_n }[/math].
- נשים לב כי עבור [math]\displaystyle{ n=0 }[/math] נקבל:
- [math]\displaystyle{ \langle f,1\rangle = \frac{a_0}{2} }[/math]
- כעת עבור [math]\displaystyle{ n\gt 0 }[/math] מתקיים:
- [math]\displaystyle{ \langle f, e^{inx}\rangle e^{inx}+\langle f, e^{-inx}\rangle e^{-inx} = }[/math]
- [math]\displaystyle{ = (\langle f, e^{inx}\rangle+\langle f, e^{-inx}\rangle)\cos(nx) + (\langle f, e^{inx}\rangle-\langle f, e^{-inx}\rangle)i\sin(nx)= }[/math]
- [math]\displaystyle{ = 2\langle f, \cos(nx)\rangle \cos(nx) + 2\langle f, i\sin(nx)\rangle i\sin(nx)= }[/math]
- [math]\displaystyle{ =a_n\cos(nx)+b_n\sin(nx) }[/math]
- (שימו לב: הi יצא מהצד הימני של המכפלה הפנימית עם מינוס)
- כלומר, טור פורייה המרוכב הוא בדיוק טור פורייה הרגיל!
הכללה לפונקציות שאינן מחזוריות
- טורי פורייה עזרו לנו לחקור פונקציות בקטע [math]\displaystyle{ [-\pi,\pi] }[/math].
- בהנתן גל [math]\displaystyle{ e^{inx} }[/math], מצאנו את ה'אמפליטודה' שלו (המקדם):
- [math]\displaystyle{ \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)e^{-inx}dx }[/math]
- (שימו לב - המכפלה הפנימית מצמידה את הפונקציה מימין, ולכן קיבלנו [math]\displaystyle{ -i }[/math]).
- מחשבה הגיונית היא שאם נרצה לחקור פונקציות בכל הממשיים, עבור גל [math]\displaystyle{ e^{isx} }[/math] נמצא את ה'אמפליטודה':
- [math]\displaystyle{ \mathcal{F}[f](s)=\frac{1}{2\pi}\int_{-\infty}^\infty f(x)e^{-isx}dx }[/math].
- כאשר האינטגרל מתכנס, הפונקציה [math]\displaystyle{ \mathcal{F}[f](s) }[/math] נקראת התמרת פורייה של הפונקציה [math]\displaystyle{ f }[/math].
- הערה - המקדם [math]\displaystyle{ \frac{1}{2\pi} }[/math] לעיתים אינו מופיע בהגדרת ההתמרה. אנחנו נראה בהמשך שיש לו קשר להתמרה ההפוכה.
- הערות כלליות:
- נסמן בדר"כ את ההתמרה של f ב[math]\displaystyle{ F(s)=\mathcal{F}(f)(s) }[/math].
- [math]\displaystyle{ F(s) }[/math] מייצגת את האמפליטודה בכל תדר, ולכן נהוג לומר שהיא מוגדרת ב'מרחב התדר'.
- לעומת זאת, [math]\displaystyle{ f(x) }[/math] מייצגת את גובה הפונקציה בכל נקודה בזמן, ונהוג לומר שהיא מוגדרת ב'מרחב הזמן'.
- לכל תדר [math]\displaystyle{ s }[/math] יש שני גלים שמייצגים אותו, [math]\displaystyle{ e^{\pm isx} }[/math].
- כפי שלמדנו, באמצעות שני הגלים ניתן לייצג כל 'פאזה'.
- נסמן ב[math]\displaystyle{ G }[/math] את אוסף הפונקציות [math]\displaystyle{ g }[/math] הרציפות למקוטעין ב[math]\displaystyle{ \mathbb{R} }[/math], עבורן האינטגרל הלא אמיתי מתכנס [math]\displaystyle{ \int_{-\infty}^\infty|g(x)|dx\lt \infty }[/math].
- לכל [math]\displaystyle{ f\in G }[/math] התמרת הפורייה מוגדרת בכל הממשיים.
- הוכחה:
- [math]\displaystyle{ \int_{-\infty}^\infty|f(x)e^{-isx}|dx = \int_{-\infty}^\infty|f(x)|dx }[/math] מתכנס.
- כיוון שהאינטגרל המגדיר את [math]\displaystyle{ F(s) }[/math] מתכנס בהחלט, הוא מתכנס.
דוגמאות
- נמצא את [math]\displaystyle{ \mathcal{F}(f)(s) }[/math] עבור [math]\displaystyle{ f(x)=e^{-|x|} }[/math].
- [math]\displaystyle{ 2\pi F(s)=\int_{-\infty}^\infty e^{-|x|}e^{-isx}dx = \int_0^\infty e^{-x}e^{-isx}dx + \int_{-\infty}^0 e^{x}e^{-isx}dx= }[/math]
- [math]\displaystyle{ =\left[\frac{e^{-x(1+is)}}{-(1+is)}\right]_0^\infty + \left[\frac{e^{x(1-is)}}{1-is}\right]_{-\infty}^0=\frac{1}{1+is} + \frac{1}{1-is} = \frac{2}{1+s^2} }[/math]
- שימו לב - השתמשנו בעובדה ש[math]\displaystyle{ e^{isx} }[/math] חסומה, ואילו [math]\displaystyle{ e^{-x}\to 0 }[/math] כאשר [math]\displaystyle{ x\to \infty }[/math].
- לכן סה"כ קיבלנו כי [math]\displaystyle{ \mathcal{F}[e^{-|x|}](s) = \frac{1}{\pi(1+s^2)} }[/math]
- נמצא את התמרת הפורייה של [math]\displaystyle{ f(x)=\begin{cases}|x| & |x|\leq \pi \\ 0 & |x|\gt \pi\end{cases} }[/math]
- [math]\displaystyle{ F(s)=\frac{1}{2\pi}\int_{-\infty}^\infty f(x)e^{-isx}dx = \frac{1}{2\pi}\int_{-\pi}^\pi |x|e^{-isx}dx = }[/math]
- [math]\displaystyle{ \frac{1}{2\pi}\int_{-\pi}^\pi |x|\cos(sx)dx - \frac{i}{2\pi}\int_{-\pi}^\pi |x|\sin(sx)dx = \frac{1}{\pi}\int_{0}^\pi x\cos(sx)dx = \frac{\sin(s\pi)}{s} + \frac{\cos(s\pi)-1}{s^2\pi} }[/math]
- שימו לב: חישוב האינטגרל שגוי עבור [math]\displaystyle{ s=0 }[/math], ניתן להציבו בנוסחא המקורית של האינטגרל או להשתמש ברציפות ההתמרה, שנלמד בהמשך.
הרצאה 7 - תכונות של התמרות פורייה
תכונות ההתמרה
- תהי [math]\displaystyle{ f\in G }[/math] אזי [math]\displaystyle{ F(s)=\mathcal{F}[f](s) }[/math] רציפה במ"ש ב[math]\displaystyle{ \mathbb{R} }[/math].
- הוכחה:
- יהי [math]\displaystyle{ \varepsilon\gt 0 }[/math]. כיוון ש [math]\displaystyle{ \int_{-\infty}^{\infty}|f(x)|dx }[/math] מתכנס, קיים [math]\displaystyle{ R }[/math] עבורו [math]\displaystyle{ \frac{1}{2\pi}\int_{|x|\gt R}|f(x)|dx \lt \frac{\varepsilon}{4} }[/math]
- עבור [math]\displaystyle{ s_1,s_2 }[/math] מתקיים כי [math]\displaystyle{ |F(s_1)-F(s_2)|\leq \frac{1}{2\pi}\int_{-\infty}^{\infty}|f(x)(e^{-is_1x}-e^{-is_2x})|dx }[/math]
- כמובן ש [math]\displaystyle{ |e^{-is_1x}-e^{-is_2x}|\leq 2 }[/math] ולכן בתחום [math]\displaystyle{ |x|\gt R }[/math] האינטגרל הנ"ל קטן מ[math]\displaystyle{ \frac{\varepsilon}{2} }[/math].
- נותר להוכיח שעבור [math]\displaystyle{ s_1,s_2 }[/math] מספיק קרובים מתקיים כי [math]\displaystyle{ \frac{1}{2\pi}\int_{-R}^{R}|f(x)(e^{-is_1x}-e^{-is_2x})|dx\lt \frac{\varepsilon}{2} }[/math]
- נראה כי [math]\displaystyle{ |e^{ix}-e^{iy}|\leq |x-y| }[/math].
- [math]\displaystyle{ |e^{ix}-e^{iy}| }[/math] הוא המרחק בין שתי נקודות על מעגל היחידה.
- [math]\displaystyle{ |x-y| }[/math] הוא הזווית בינהן, כלומר אורך הקשת בינהן.
- אורך הקשת בוודאי גדול או שווה למרחק הישר בין שתי הנקודות.
- לכן [math]\displaystyle{ |e^{-is_1x}-e^{-is_2x}|\leq |x||s_1-s_2| }[/math]
- כיוון ש[math]\displaystyle{ |x|\leq R }[/math] והפונקציה [math]\displaystyle{ f }[/math] חסומה בתחום זה, עבור [math]\displaystyle{ |s_1-s_2| }[/math] מספיק קטן נקבל את הדרוש.
- רשימת תכונות נוספות של ההתמרה:
- [math]\displaystyle{ \mathcal{F}[f+a\cdot g] = \mathcal{F}[f]+a\mathcal{F}[g] }[/math]
- [math]\displaystyle{ \mathcal{F}[f](-s) = \overline{\mathcal{F}[f](s)} }[/math]
- אם [math]\displaystyle{ f }[/math] ממשית וזוגית, גם [math]\displaystyle{ \mathcal{F}[f](s) }[/math] ממשית וזוגית.
- הזזה במרחב הזמן:
- אם [math]\displaystyle{ g(x)=f(ax+b) }[/math], אזי [math]\displaystyle{ \mathcal{F}(g)(s) = \frac{1}{|a|}e^{\frac{isb}{a}}\mathcal{F}[f](\frac{s}{a}) }[/math]
- אם [math]\displaystyle{ a=1 }[/math] אז נקבל שהזזה במרחב הזמן שקולה לסיבוב במרחב התדר (כפל ב[math]\displaystyle{ e^{isb} }[/math] משנה את הזוית).
- הזזה במרחב התדר:
- [math]\displaystyle{ \mathcal{F}[e^{ibx}f(x)](s) = \mathcal{F}[f](s-b) }[/math]
- באופן דומה, קיבלנו שסיבוב בזמן שקול להזזה בתדר.
- התמרת הנגזרת:
- נניח [math]\displaystyle{ f,f'\in G }[/math] ונניח כי [math]\displaystyle{ f' }[/math] רציפה ומתקיים כי [math]\displaystyle{ \lim_{x\to \pm\infty}f(x)=0 }[/math], אזי:
- [math]\displaystyle{ \mathcal{F}[f'](s)=is\mathcal{F}[f](s) }[/math]
- הוכחה:
- [math]\displaystyle{ \mathcal{F}[f'](s) = \frac{1}{2\pi}\int_{-\infty}^{\infty} f'(x)e^{-isx}dx }[/math]
- נבצע אינטגרציה בחלקים ונקבל כי
- [math]\displaystyle{ \mathcal{F}[f'](s) = \frac{1}{2\pi}(fe^{-isx})_{-\infty}^{\infty} + \frac{is}{2\pi} \int_{-\infty}^{\infty} f(x)e^{-isx}dx }[/math].
- כיוון ש[math]\displaystyle{ e^{-isx} }[/math] חסומה, יחד עם הנתון נובע כי [math]\displaystyle{ (fe^{-isx})_{-\infty}^{\infty}=0 }[/math].
- לכן סה"כ קיבלנו כי [math]\displaystyle{ \mathcal{F}[f'](s)=is\mathcal{F}[f](s) }[/math]
- נגזרת ההתמרה:
- תהי [math]\displaystyle{ f\in G }[/math] רציפה כך ש[math]\displaystyle{ xf(x)\in G }[/math] אזי:
- [math]\displaystyle{ \mathcal{F}[xf(x)](s)=i\frac{d}{ds}\mathcal{F}[f](s) }[/math]
- הוכחה:
- [math]\displaystyle{ i\frac{d}{ds}\mathcal{F}[f](s) = i \frac{d}{ds} \frac{1}{2\pi}\int_{-\infty}^{\infty} f(x)e^{-isx}dx = \frac{i}{2\pi}\int_{-\infty}^{\infty} f(x)\frac{d}{ds}e^{-isx}dx = \frac{-i^2}{2\pi}\int_{-\infty}^{\infty} xf(x)e^{-isx} = \mathcal{F}[xf(x)](s) }[/math]
- אנחנו צריכים להצדיק את ההכנסה של הנגזרת אל תוך האינטגרל:
- נסמן [math]\displaystyle{ F_n(s)=\frac{1}{2\pi}\int_{-n}^{n} f(x)e^{-isx}dx }[/math]
- ברור ש[math]\displaystyle{ F_n(s)\to F(s) }[/math], נוכיח שסדרת הנגזרות מתכנסת במ"ש ולכן מתכנסת לנגזרת של [math]\displaystyle{ F(s) }[/math].
- עבור אינטגרל סופי מותר להחליף את סדר הנגזרת והאינטגרל בזכות פוביני.
- אכן [math]\displaystyle{ F_n'(s) }[/math] מתכנסות במ"ש כיוון שהאינטגרל [math]\displaystyle{ \int_{-\infty}^\infty |xf(x)|dx }[/math] מתכנס, והרי [math]\displaystyle{ |xf(x)e^{-isx}|=|xf(x)| }[/math] ואכן אינו תלוי בs.
דוגמאות
- ראינו כי [math]\displaystyle{ \mathcal{F}[e^{-|x|}](s) = \frac{1}{\pi(1+s^2)} }[/math]
- לכן על ידי הזזה בזמן נקבל כי:
- [math]\displaystyle{ \mathcal{F}[e^{-|1-2x|}](s) = \frac{e^{\frac{-is}{2}}}{2\pi (1+(-\frac{s}{2})^2)} }[/math]
- נסמן [math]\displaystyle{ F(s)=\mathcal{F}[e^{-x^2}] }[/math].
- כעת [math]\displaystyle{ \mathcal{F}[xe^{-x^2}] = iF' }[/math] לפי הנוסחא של נגזרת ההתמרה.
- מצד שני, [math]\displaystyle{ \mathcal{F}[-2xe^{-x^2}] = isF }[/math] לפי הנוסחא של התמרת הנגזרת.
- ביחד נקבל כי [math]\displaystyle{ isF = -2iF' }[/math], ולכן [math]\displaystyle{ sF=-2F' }[/math].
- נפתור את המד"ר:
- נכפול בגורם אינטגרציה [math]\displaystyle{ \frac{1}{2}e^{\frac{s^2}{4}} }[/math] ונקבל [math]\displaystyle{ (e^{\frac{s^2}{4}}F)'=0 }[/math]
- לכן [math]\displaystyle{ F=Ce^{-\frac{s^2}{4}} }[/math]
- נציב [math]\displaystyle{ s=0 }[/math]
- [math]\displaystyle{ 2\pi C=F(0)=\int_{-\infty}^\infty e^{-x^2}dx }[/math], נחשב אינטגרל מפורסם זה בהמשך.
הרצאה 8 - התמרה הפוכה
- בטורי פורייה, מקדמי הפורייה היו האמפליטודות של התדרים, וכאשר סכמנו את הגלים קיבלנו חזרה את הפונקציה לפי משפט דיריכלה.
- כעת התדרים שלנו הם כל הממשיים, ולכן הסכימה שלהם היא בעצם אינטגרל.
- האמפליטודה של כל תדר מרוכב [math]\displaystyle{ e^{isx} }[/math] היא התמרת הפורייה [math]\displaystyle{ F(s) }[/math], ולכן אנחנו מצפים לקבל:
- [math]\displaystyle{ f(x)=\int_{-\infty}^\infty F(s)e^{isx}ds=\mathcal{F}^{-1}[F](x) }[/math]
- משפט ההתמרה ההפוכה:
- תהי [math]\displaystyle{ f\in G }[/math], אזי בכל נקודה בה קיימות הנגזרות החד צדדיות מתקיים כי:
- [math]\displaystyle{ \frac{f(x^+)+f(x^-)}{2}=\lim_{n\to\infty}\int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\mathcal{F}[f](s)e^{isx}ds }[/math]
- שימו לב שהאינטגרל [math]\displaystyle{ \int_{-\infty}^{\infty}\mathcal{F}[f](s)e^{isx}ds }[/math] לא חייב להתכנס, אבל אם הוא מתכנס הוא שווה לגבול לעיל.
דוגמא
- ראינו ש[math]\displaystyle{ \mathcal{F}[e^{-x^2}] = Ce^{-\frac{s^2}{4}} =\frac{1}{2\pi}\int_{-\infty}^\infty e^{-x^2}e^{-isx}dx }[/math]
- כיוון ש[math]\displaystyle{ e^{-x^2} }[/math] רציפה וגזירה, וכיוון ש [math]\displaystyle{ e^{-\frac{s^2}{4}}\in G }[/math] לפי משפט ההתמרה ההפוכה נקבל כי:
- [math]\displaystyle{ \mathcal{F}^{-1}[Ce^{-\frac{s^2}{4}}](x) = e^{-x^2} }[/math]
- כלומר [math]\displaystyle{ e^{-x^2}=\int_{-\infty}^\infty Ce^{-\frac{s^2}{4}}e^{isx}ds }[/math]
- נציב [math]\displaystyle{ t=\frac{s}{2} }[/math] ונקבל:
- [math]\displaystyle{ e^{-x^2} = 2C\int_{-\infty}^\infty e^{-t^2}e^{-i(-2x)t}dt = 2C\cdot 2\pi Ce^{-\frac{(-2x)^2}{4}} }[/math]
- ולכן [math]\displaystyle{ 4C^2\pi = 1 }[/math], ומכאן [math]\displaystyle{ C=\frac{1}{2\sqrt{\pi}} }[/math]
- נזכור בנוסף שראינו כי [math]\displaystyle{ 2\pi C = \int_{-\infty}^\infty e^{-x^2}dx }[/math].
- לכן נובע כי [math]\displaystyle{ \int_{-\infty}^\infty e^{-x^2}dx = \sqrt{\pi} }[/math]
דוגמא
- נביט ב[math]\displaystyle{ f(x)=\begin{cases}1 & |x|\lt 1 \\ 0 & |x|\gt 1\end{cases} }[/math]
- [math]\displaystyle{ \mathcal{F}[f](s) = \frac{sin(s)}{\pi s} }[/math]
- [math]\displaystyle{ \lim \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}} \frac{sin(s)}{\pi s}e^{is}ds = \frac{1}{2} }[/math] (הצבנו x=1, הנקודה בה f אינה רציפה).
הקדמה לקראת הוכחת משפט ההתמרה ההפוכה
- כעת נוכיח מספר טענות הדרושות לנו לצורך הוכחת משפט ההתמרה ההפוכה.
למת רימן-לבג
- ראינו גרסא של למת רימן-לבג עבור טורי פוריה, לפי מקדמי הפורייה שואפים לאפס.
- כעת ננסח ונוכיח גרסא עבור התמרות פורייה:
- תהי [math]\displaystyle{ f\in G }[/math], אזי [math]\displaystyle{ \lim_{s\to\pm\infty}\mathcal{F}[f](s)=0 }[/math]
- (כלומר, האמפליטודות שואפות לאפס כאשר התדר שואף לאינסוף)
- נוכיח את הלמה:
- צ"ל כי[math]\displaystyle{ \lim_{s\to\pm\infty}\frac{1}{2\pi}\int_{-\infty}^\infty f(x)e^{-isx}dx =0 }[/math]
- נשים לב כי [math]\displaystyle{ e^{-isx}=\cos(sx)-i\sin(sx) }[/math].
- לכן מספיק לנו להוכיח כי [math]\displaystyle{ \lim_{s\to\pm\infty}\frac{1}{2\pi}\int_{-\infty}^\infty f(x)\cos(sx)dx =0 }[/math] (ההוכחה עבור סינוס דומה).
- כיוון ש[math]\displaystyle{ f\in G }[/math] האינטגרל [math]\displaystyle{ \int_{-\infty}^{\infty}|f(x)|dx }[/math] מתכנס.
- לכן קיים [math]\displaystyle{ M }[/math] עבורו [math]\displaystyle{ \int_{|x|\gt M}|f(x)|dx\lt \frac{\varepsilon}{2} }[/math].
- לכן [math]\displaystyle{ |\int_{|x|\gt M}f(x)\cos(sx)dx|\leq \int_{|x|\gt M}|f(x)|dx \lt \frac{\varepsilon}{2} }[/math]
- לכן מספיק לנו להוכיח כי עבור [math]\displaystyle{ |s| }[/math] מספיק גדול מתקיים [math]\displaystyle{ |\int_{-M}^{M}f(x)\cos(sx)dx| \lt \frac{\varepsilon}{2} }[/math]
- (עבור [math]\displaystyle{ M=\pi }[/math] ו[math]\displaystyle{ s\in\mathbb{N} }[/math] כבר הוכחנו טענה זו בעזרת פרסבל, כעת נשתמש בשיטות אחרות.)
- נשים לב כי בכל קטע מתקיים:
- [math]\displaystyle{ \lim_{s\to\pm\infty}\int_{x_1}^{x_2}\cos(sx)dx = \lim_{s\to\pm\infty}\frac{\sin(sx_2)-\sin(sx_1)}{s}=0 }[/math]
- כיוון ש[math]\displaystyle{ f }[/math] רציפה למקוטעין היא אינטגרבילית ב[math]\displaystyle{ [-M,M] }[/math].
- לכן ניתן לבחור פונקצית מדרגות [math]\displaystyle{ h }[/math] עבורה מתקיים [math]\displaystyle{ \int_{-M}^M |f-h|dx \lt \frac{\varepsilon}{4} }[/math] (האינטגרל על פונקצית המדרגות הינו סכום דרבו תחתון מספיק קרוב).
- כמו כן מתקיים:
- [math]\displaystyle{ \int_{-M}^Mh\cos(sx)dx = \sum \int_{x_{i-1}}^{x_i}m_i\cos(sx)dx }[/math]
- כיוון שמדובר בסכום סופי של ביטויים ששואפים לאפס, הסכום גם שואף לאפס.
- סה"כ [math]\displaystyle{ \int_{-M}^{M}f(x)\cos(sx)dx = \int_{-M}^{M}(f(x)-h(x))\cos(sx)dx + \int_{-M}^{M}h(x)\cos(sx)dx }[/math]
- מתקיים כי [math]\displaystyle{ |\int_{-M}^{M}(f(x)-h(x))\cos(sx)dx|\leq \int_{-M}^{M}|f(x)-h(x)|dx \lt \frac{\varepsilon}{4} }[/math]
- עבור [math]\displaystyle{ |s| }[/math] מספיק גדול מתקיים כי [math]\displaystyle{ |\int_{-M}^{M}h(x)\cos(sx)dx|\lt \frac{\varepsilon}{4} }[/math]
- סה"כ קיבלנו כי עבור [math]\displaystyle{ |s| }[/math] מספיק גדול מתקיים [math]\displaystyle{ |\int_{-\infty}^{\infty}f(x)\cos(sx)sx|\lt \varepsilon }[/math]
טענת עזר
- תהי [math]\displaystyle{ f\in G }[/math] ותהי x נק' בה הנגזרות החד צדדיות קיימות, אזי:
- [math]\displaystyle{ \lim_{n\to\infty} \frac{1}{\pi}\int_0^{\infty} f(x+t)\frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{f(x^+)}{2} }[/math]
- [math]\displaystyle{ \lim_{n\to\infty} \frac{1}{\pi}\int_{-\infty}^{0} f(x+t)\frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{f(x^-)}{2} }[/math]
- נוכיח את הטענה הראשונה, הטענה השנייה דומה.
- נגדיר את הפונקציה [math]\displaystyle{ g(t)=\begin{cases}\frac{f(x+t)}{t}& x\in [\pi,\infty)\\ 0 & x\in (-\infty,\pi)\end{cases} }[/math]
- כיוון ש[math]\displaystyle{ f\in G }[/math] נובע שגם [math]\displaystyle{ g\in G }[/math] הרי [math]\displaystyle{ \left|\frac{f(x+t)}{t}\right|\leq |f(x+t)| }[/math] עבור [math]\displaystyle{ t\gt \pi }[/math].
- לכן לפי למת רימן-לבג נובע כי [math]\displaystyle{ \lim_{s\to\infty}\int_{-\infty}^{\infty}g(t)\sin(st)dt = 0 }[/math]
- בפרט מתקיים גבול הסדרה:
- [math]\displaystyle{ \lim_{n\to\infty} \int_{-\infty}^{\infty}g(t)\sin\left((n+\frac{1}{2})t\right)dt =0 }[/math]
- אבל [math]\displaystyle{ \int_{-\infty}^{\infty}g(t)\sin\left((n+\frac{1}{2})t\right)dt = \int_\pi^\infty \frac{f(x+t)}{t}\sin\left((n+\frac{1}{2})t\right)dt }[/math]
- לכן נותר להוכיח כי [math]\displaystyle{ \lim_{n\to\infty}\frac{1}{\pi}\int_0^{\pi} f(x+t)\frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{f(x^+)}{2} }[/math]
- נגדיר את הפונקציה [math]\displaystyle{ h(t)=f(x+t)\frac{2\sin(\frac{t}{2})}{t} }[/math].
- אם נתקן את אי הרציפות הסליקה של [math]\displaystyle{ \frac{2\sin(\frac{t}{2})}{t} }[/math] נקבל טור טיילור שגזיר אינסוף פעמים.
- לכן הפוקנציה [math]\displaystyle{ h }[/math] רציפה למקוטעין ובעלת נגזרות חד צדדיות קיימות.
- כעת נשים לב כי:
- [math]\displaystyle{ \frac{1}{\pi}\int_0^{\pi} f(x+t)\frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{1}{\pi}\int_0^{\pi} h(t)\frac{\sin\left((n+\frac{1}{2})t\right)}{2\sin(\frac{t}{2})}dt = \frac{1}{\pi}\int_0^{\pi} h(t)D_n(t)dt }[/math]
- לפי ההוכחה של משפט דיריכלה להתכנסות טורי פורייה, הגבול של הביטוי הזה שווה ל[math]\displaystyle{ \frac{h(0^+)}{2} = \frac{f(x^+)}{2} }[/math].
דוגמא
- טענה:
- [math]\displaystyle{ \int_0^\infty \frac{\sin(x)}{x}dx = \frac{\pi}{2} }[/math]
- הוכחה:
- ראשית, אנו יודעים כי האינטגרל מתכנס לפי מבחן דיריכלה לאינטגרלים לא אמיתיים.
- לכן מתקיים כי [math]\displaystyle{ \int_0^\infty \frac{\sin(x)}{x}dx =\lim_{n\to\infty} \int_0^{(n+\frac{1}{2})\pi}\frac{\sin(x)}{x}dx }[/math]
- נבצע הצבה [math]\displaystyle{ t=\frac{x}{n+\frac{1}{2}} }[/math] ונקבל כי:
- [math]\displaystyle{ \int_0^{(n+\frac{1}{2})\pi}\frac{\sin(x)}{x}dx = \int_0^\pi \frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt }[/math]
- עבור [math]\displaystyle{ f(x)=1 }[/math], לפי הוכחת טענת העזר נקבל כי הגבול הוא [math]\displaystyle{ \frac{\pi}{2} }[/math]
הוכחת משפט ההתמרה ההפוכה
- [math]\displaystyle{ \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\mathcal{F}[f](s)e^{isx}ds = \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\left[\frac{1}{2\pi}\int_{-\infty}^\infty f(y)e^{-isy}dy\right]e^{isx}ds= }[/math]
- [math]\displaystyle{ =\frac{1}{2\pi} \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\int_{-\infty}^\infty f(y)e^{is(x-y)}dyds }[/math]
- נחליף את סדר האינטגרציה (הצדקה בהמשך), ונקבל:
- [math]\displaystyle{ \frac{1}{2\pi}\int_{-\infty}^\infty\int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}f(y)e^{is(x-y)}dsdy = }[/math]
- [math]\displaystyle{ \frac{1}{2\pi}\int_{-\infty}^\infty f(y) \left[\frac{e^{is(x-y)}}{i(x-y)}\right]_{-(n+\frac{1}{2})}^{n+\frac{1}{2}} dy = }[/math]
- [math]\displaystyle{ \frac{1}{2\pi}\int_{-\infty}^\infty f(y) \frac{2\sin\left((n+\frac{1}{2})(x-y)\right)}{(x-y)} dy }[/math]
- נציב [math]\displaystyle{ t=y-x }[/math] ונקבל:
- [math]\displaystyle{ \frac{1}{\pi}\int_{-\infty}^\infty f(x+t) \frac{\sin\left((n+\frac{1}{2})t\right)}{t}dt = \frac{f(x^+)+f(x^-)}{2} }[/math]
כאשר המעבר האחרון הוא בזכות טענת העזר לעיל.
הצדקת החלפת סדר האינטגרציה
- נביט בסדרה [math]\displaystyle{ u_k(s)=\int_{-k}^k f(y)e^{is(x-y)}dy }[/math], שמתכנסת כמובן ל[math]\displaystyle{ \int_{-\infty}^\infty f(y)e^{is(x-y)}dy }[/math]
- מתקיים כי [math]\displaystyle{ |\int_{-\infty}^\infty f(y)e^{is(x-y)}dy - u_k(s)| \leq \int_{|y|\gt k} |f(y)e^{is(x-y)}|dy = \int_{|y|\gt k} |f(y)|dy\to 0 }[/math]
- (נתון כי [math]\displaystyle{ f\in G }[/math])
- לכן הסדרה מתכנסת במ"ש ומותר לבצע אינטגרציה איבר איבר:
- [math]\displaystyle{ \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\int_{-\infty}^\infty f(y)e^{is(x-y)}dyds = \lim_{k\to\infty} \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}} u_k(s)ds }[/math]
- לפי פוביני מותר לנו להחליף את סדר האינטגרציה ונקבל כי
- [math]\displaystyle{ \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}\int_{-\infty}^\infty f(y)e^{is(x-y)}dyds = \lim_{k\to\infty} \int_{-k}^k \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}f(y)e^{is(x-y)}dsdy = \int_{-\infty}^\infty \int_{-(n+\frac{1}{2})}^{n+\frac{1}{2}}f(y)e^{is(x-y)}dsdy }[/math]
- שימו לב שהאינטגרל הלא אמיתי אכן מתכנס (כפי שהוכחנו לעיל) ולכן שווה לגבול.
הרצאה 9 - קונבולוציה, משוואת החום על מוט אינסופי
- תהיינה [math]\displaystyle{ f,g:\mathbb{R}\to\mathbb{C} }[/math] פונקציות, נגדיר את הקונבולוציה ביניהן להיות:
- [math]\displaystyle{ f*g(x) = \int_{-\infty}^\infty f(x-y)g(y)dy }[/math].
- מוטיבציה לדוגמא:
- אם [math]\displaystyle{ f,g }[/math] הן פונקציות צפיפות של משתנים מקריים, מהי פונקציית הצפיפות של סכום המשתנים?
- הסיכוי שסכום המשתנים יהיה x, הוא סכום מכפלות הסיכויים שמשתנה אחד יהיה שווה y והשני יהיה שווה x-y.
- הקונבולוציה היא אבלית:
- [math]\displaystyle{ g*f = \int_{-\infty}^\infty g(x-y)f(y)dy = \{t=x-y,dt=-dy\} = \int_{-\infty}^\infty g(t)f(x-t)dt = f*g }[/math]
- שימו לב: בנושא זה נבצע החלפת סדר אינטגרציה, אך לא נצדיק החלפה זו כיוון שהיא דורשת העמקה רבה.
- ניתן להעמיק ע"י קריאה בספר Fourier Analysis של T.W.Korner
- משפט הקונבולוציה:
- תהיינה [math]\displaystyle{ f,g\in G }[/math] רציפות וחסומות אזי [math]\displaystyle{ \mathcal{F}[f*g] = 2\pi \cdot \mathcal{F}[f] \cdot \mathcal{F}[g] }[/math]
- הסבר המשפט (לא הוכחה מלאה, כיוון שאנו מחליפים סדר אינטגרציה ללא הצדקה):
- [math]\displaystyle{ \mathcal{F}[f*g] = \frac{1}{2\pi}\int_{-\infty}^\infty \left[\int_{-\infty}^\infty f(x-y)g(y)dy\right]e^{-isx}dx = }[/math]
- [math]\displaystyle{ = \frac{1}{2\pi}\int_{-\infty}^\infty \int_{-\infty}^\infty f(x-y)e^{-is(x-y)}g(y)e^{-isy}dydx = }[/math]
- [math]\displaystyle{ = \frac{1}{2\pi}\int_{-\infty}^\infty \int_{-\infty}^\infty f(x-y)e^{-is(x-y)}g(y)e^{-isy}dxdy = }[/math]
- [math]\displaystyle{ = \frac{1}{2\pi}\int_{-\infty}^\infty \left[\int_{-\infty}^\infty f(x-y)e^{-is(x-y)}dx\right] g(y)e^{-isy}dy = }[/math]
- [math]\displaystyle{ = \frac{1}{2\pi}\int_{-\infty}^\infty \left[\int_{-\infty}^\infty f(t)e^{-ist}dt\right] g(y)e^{-isy}dy = }[/math]
- [math]\displaystyle{ = 2\pi\left(\frac{1}{2\pi}\int_{-\infty}^\infty f(t)e^{-ist}dt\right) \cdot \left( \frac{1}{2\pi}\int_{-\infty}^\infty g(y)e^{-isy}dy\right) =2\pi \cdot \mathcal{F}[f] \cdot \mathcal{F}[g] }[/math]
משוואת החום על מוט אינסופי
- אם פונקצית החום על מוט אינסופי היא [math]\displaystyle{ u(x,t) }[/math], היא מקיימת את המשוואה [math]\displaystyle{ u_t-ku_{xx}=0 }[/math].
- נניח גם כי תנאי ההתחלה הם [math]\displaystyle{ u(x,0)=f(x) }[/math] (זה החום בכל נקודה במוט בזמן 0).
- נבצע התמרת פורייה של הפתרון לפי המשתנה x:
- [math]\displaystyle{ U(s,t)=\frac{1}{2\pi}\int_{-\infty}^{\infty} u(x,t)e^{-isx}dx }[/math]
- נגזור לפי המשתנה t:
- [math]\displaystyle{ U_t(s,t) = \frac{1}{2\pi}\int_{-\infty}^{\infty} u_t(x,t)e^{-isx}dx }[/math]
- (נניח כי הפתרון מקיים את התנאים שמאפשרים להחליף את סדר הגזירה והאינטגרציה, לא נרחיב על כך בהמשך)
- כיוון ש[math]\displaystyle{ u_t-ku_{xx}=0 }[/math] נקבל כי:
- [math]\displaystyle{ U_t(s,t) = \frac{k}{2\pi}\int_{-\infty}^{\infty} u_{xx}(x,t)e^{-isx}dx }[/math]
- נזכר בנוסחאת התמרת הנגזרת [math]\displaystyle{ \mathcal{F}[f']=is\mathcal{F}[f] }[/math]
- ולכן נקבל כי:
- [math]\displaystyle{ U_t(s,t) = -s^2 \frac{k}{2\pi}\int_{-\infty}^\infty u(x,t)e^{-isx}dx = -ks^2 U(s,t) }[/math]
- זו מד"ר פשוטה שפתרונה הוא:
- [math]\displaystyle{ U(s,t) = A(s)e^{-ks^2 t} }[/math]
- נציב את תנאי ההתחלה [math]\displaystyle{ t=0 }[/math] ונקבל כי
- [math]\displaystyle{ A(s) = U(s,0) = \frac{1}{2\pi}\int_{-\infty}^{\infty} u(x,0)e^{-isx}dx = \frac{1}{2\pi}\int_{-\infty}^{\infty} f(x)e^{-isx}dx = \mathcal{F}[f] }[/math]
- לכן בעצם מתקיים כי [math]\displaystyle{ U(s,t)= F(s)e^{-ks^2 t} }[/math]
- קיבלנו שההתמרה של הפתרון היא מכפלה של שתי התמרות, ולכן הפתרון הוא הקונבולוציה של שתי הפונקציות המקוריות.
- נחפש את ההתמרה ההפוכה של [math]\displaystyle{ e^{-ks^2 t} }[/math]
- נזכור כי [math]\displaystyle{ \mathcal{F}[e^{-x^2}] = \frac{1}{2\sqrt{\pi}} e^{-\frac{s^2}{4}} }[/math]
- [math]\displaystyle{ \mathcal{F}^{-1}[e^{-ks^2 t}]=\int_{-\infty}^\infty e^{-ks^2 t}e^{isx}ds = \{s=\frac{u}{2\sqrt{kt}}\}= }[/math]
- [math]\displaystyle{ =\frac{1}{2\sqrt{kt}}\int_{-\infty}^\infty e^{-\frac{u^2}{4}}e^{iu(\frac{x}{2\sqrt{kt}})}du = \frac{2\sqrt{\pi}}{2\sqrt{kt}} \mathcal{F}^{-1}[\frac{1}{2\sqrt{\pi}}e^{-\frac{u^2}{4}}](\frac{x}{2\sqrt{kt}}) = \frac{\sqrt{\pi}}{\sqrt{kt}}e^{-\frac{x^2}{4kt}} }[/math]
- נסמן פונקציה זו ב[math]\displaystyle{ p(x,t)=\frac{\sqrt{\pi}}{\sqrt{kt}}e^{-\frac{x^2}{4kt}} }[/math]
- לכן עבור פתרון מד"ח החום u מתקיים כי:
- [math]\displaystyle{ \mathcal{F}[u] = \mathcal{F}[f]\cdot \mathcal{F}[p] }[/math]
- ולכן לפי משפט הקונבולוציה מתקיים כי
- [math]\displaystyle{ u(x,t) = \frac{1}{2\pi} f*p(x,t) }[/math]
- שימו לב שהקונבולוציה היא לפי המשתנה x.
- לכן
- [math]\displaystyle{ u(x,t) = \frac{1}{2\pi}\int_{-\infty}^\infty f(y)p(x-y,t)dy = \frac{1}{2\sqrt{\pi kt}}\int_{-\infty}^\infty f(y)e^{-\frac{(x-y)^2}{4kt}}dy }[/math]
- שימו לב שבפתרון הסופי מופיעה פונקצית תנאי ההתחלה, ואין צורך לחשב את ההתמרה שלה.
הרצאה 10 - משפט הדגימה של שנון
משפט הדגימה של שנון
- תהי פונקציה f. ברור שבהנתן הערכים של f על השלמים [math]\displaystyle{ f(0),f(\pm 1),f(\pm 2),... }[/math] לא ניתן להסיק כלום על ערכיה האחרים (אפילו אם היא רציפה וגזירה).
- בפרט אם נדגום באופן דומה את הפונקציה [math]\displaystyle{ sin(x) }[/math] בנקודות [math]\displaystyle{ 2\pi n }[/math] אנחנו עשויים לחשוד שהיא קבועה לחלוטין.
- מה יקרה אם נדגום גל בקצב מהיר יותר מהתדר שלו?
- במילים פשוטות, משפט הדגימה של שנון אומר שבהנתן פונקציה שהתדרים שלה חסומים, אם נדגום אותה בקצב מהיר פי 2 מהתדר המקסימלי שלה, נוכל לשחזר אותה לחלוטין.
- כעת ננסח את המשפט במדויק, יחד עם ניסוח התנאים הנחוצים על הפונקציות.
- עד כה דיברנו על תדר כמדד לקצב בו הפונקציה חוזרת על עצמה, כעת נגדיר אותו במדויק:
- בהנתן פונקציה עם מחזור [math]\displaystyle{ t }[/math] נגדיר את התדר של המחזור להיות [math]\displaystyle{ \frac{1}{t} }[/math].
- דוגמאות:
- התדר של [math]\displaystyle{ \sin(x) }[/math] הוא [math]\displaystyle{ \frac{1}{2\pi} }[/math]
- התדר של [math]\displaystyle{ \sin(\pi x) }[/math] הוא [math]\displaystyle{ \frac{1}{2} }[/math]
- באופן כללי, התדר של [math]\displaystyle{ sin(\pi t x) }[/math] הוא [math]\displaystyle{ \frac{t}{2} }[/math] כיוון ש [math]\displaystyle{ \sin(\pi t(x+\frac{2}{t})) = \sin(\pi t x) }[/math]
- התדר של [math]\displaystyle{ e^{isx} }[/math] הוא [math]\displaystyle{ \frac{|s|}{2\pi} }[/math] כיוון ש [math]\displaystyle{ e^{is(x+\frac{2\pi}{|s|})} = e^{isx\pm i2\pi} =e^{isx} }[/math]
- משפט הדגימה של שנון:
- תהי [math]\displaystyle{ f\in G }[/math] רציפה ובעלת נגזרת חד צדדיות הקיימות בכל נקודה, שתדריה חסומים על ידי [math]\displaystyle{ t }[/math], אזי בהנתן דגימה שלה בתדר [math]\displaystyle{ 2t }[/math] ניתן לשחזר אותה בכל הממשיים (כלומר היא נקבעת באופן יחיד על ידי הדגימות).
- שימו לב: הכוונה בכך שתדריה של הפונקציה חסומים, היא למעשה ש[math]\displaystyle{ \mathcal{F}[f](s)=0 }[/math] לכל [math]\displaystyle{ \frac{|s|}{2\pi}\gt t }[/math].
הוכחת משפט הדגימה
- כיוון שהתמרת הפורייה מתאפסת מחוץ לקטע [math]\displaystyle{ [-2\pi t,2\pi t] }[/math], ניתן לקבוע כי
- [math]\displaystyle{ \int_{-\infty}^\infty \mathcal{F}[f](s)e^{isx}ds = \int_{-2\pi t}^{2\pi t}\mathcal{F}[f](s)e^{isx}ds }[/math]
- ובפרט האינטגרל מתכנס.
- לפי משפט ההתמרה ההפוכה, נובע כי [math]\displaystyle{ f(x)= \int_{-2\pi t}^{2\pi t}\mathcal{F}[f](s)e^{isx}ds }[/math]
- כעת, נתונה לנו סדרת הדגימות בתדר [math]\displaystyle{ 2t }[/math]:
- [math]\displaystyle{ c_n = f\left(\frac{n}{2t}\right), n\in\mathbb{Z} }[/math]
- נציב אותן בנוסחא שמצאנו לעיל:
- [math]\displaystyle{ c_n = \int_{-2\pi t}^{2\pi t}\mathcal{F}[f](s)e^{is\left(\frac{n}{2t}\right)}ds }[/math]
- נבצע הצבה [math]\displaystyle{ \frac{s}{2t}=-x }[/math] ונקבל:
- [math]\displaystyle{ c_n = \int_{-\pi}^\pi \mathcal{F}[f](-2tx)e^{-inx}dx }[/math]
- אבל אלה בדיוק מקדמי פוריה (פרט לקבוע [math]\displaystyle{ \frac{1}{2\pi} }[/math]) של הפונקציה [math]\displaystyle{ \mathcal{F}[f](-2tx) }[/math].
- כיוון שההתמרה חסומה בתדר, עבור [math]\displaystyle{ |x|\geq \pi }[/math] מתקיים כי [math]\displaystyle{ \mathcal{F}[f](-2tx)=0 }[/math] (זכרו כי ההתמרה רציפה, ולכן מתאפסת גם בקצוות).
- לכן [math]\displaystyle{ \mathcal{F}[f](-2tx) }[/math] נקבעת על ידי ערכיה בקטע [math]\displaystyle{ (-\pi,\pi) }[/math], והם נקבעים באופן יחיד על ידי מקדמי הפורייה (מסקנה מפרסבל).
- לבסוף, כפי שראינו לעיל, הפונקציה f נקבעת באופן יחיד על ידי ההתמרה (בזכות משפט ההתמרה ההפוכה).
הערות
- שימו לב שלא ניתן באופן פרקטי לדגום אות אנלוגי באינסוף נקודות.
- מה יקרה אם נדגום במספר סופי של נקודות ונניח כי הפונקציה ממשיכה באופן מחזורי?
- נקבל פונקציה שאינה שייכת ל[math]\displaystyle{ G }[/math], כיוון שהאינטגרל שלה לא יכול להתכנס בכל הממשיים.
- בהמשך, נראה אנלוגיה למשפט הדגימה של שנון בהתמרת פורייה הבדידה.
הרצאה 11 - התמרת פורייה הבדידה
DFT - Discrete Fourier transform
- תהי סדרת נקודות [math]\displaystyle{ a_0,...,a_{N-1} \in \mathbb{C} }[/math], התמרת הפורייה הבדידה שלה היא סדרת הנקודות [math]\displaystyle{ A_0,...,A_{N-1}\in\mathbb{C} }[/math] המוגדרת ע"י:
- [math]\displaystyle{ A_n = \sum_{k=0}^{N-1} a_k e^{-2\pi i n\frac{k}{N}} }[/math]
- שימו לב שכמות הפעולות הנדרשות לחישוב ההתמרה באופן ישיר היא סדר גודל של [math]\displaystyle{ N^2 }[/math].
- התמרת פורייה המהירה (FFT) מבצעת את אותו חישוב בכמות פעולות בסדר גודל של [math]\displaystyle{ N\log(N) }[/math].
משמעות ההתמרה
- תהי פונקציה f. נדגום ממנה [math]\displaystyle{ N }[/math] נקודות בתדר [math]\displaystyle{ t }[/math], כלומר נתון לנו:
- [math]\displaystyle{ f(0),f(\frac{1}{t}),f(\frac{2}{t}),...,f(\frac{N-1}{t}) }[/math]
- נסמן נקודות אלה ב[math]\displaystyle{ a_k=f(\frac{k}{t}) }[/math]
- אנו רוצים לפרק אותה לסכום של גלים:
- [math]\displaystyle{ f(x)=B_0e^{2\pi i \cdot 0\cdot\frac{t}{N}x}+ B_1e^{2\pi i \cdot 1\cdot\frac{t}{N}x}+B_2e^{2\pi i \cdot 2\cdot\frac{t}{N}x}+...+B_{N-1}e^{2\pi i \cdot (N-1)\cdot\frac{t}{N}x} }[/math]
- כיוון שהתדר של [math]\displaystyle{ e^{isx} }[/math] הוא [math]\displaystyle{ \frac{|s|}{2\pi} }[/math] נובע כי הגלים הללו הם בתדרים [math]\displaystyle{ 0,\frac{t}{N},\frac{2t}{N},...,\frac{(N-1)t}{N} }[/math]
- שימו לב - ככל שנדגום יותר נקודות נקבל יותר מגוון של תדרים. מצד שני, נביט בחלון זמן יותר ארוך ונפספס שינויי תדרים מהירים יותר.
- נוכיח שפירוק זה תמיד אפשרי כך שיהיה שיוויון בכל נקודות הדגימה, ונקשר בין סדרת המקדמים להתמרת הפורייה של נקודות הדגימה.
- נביט בפונקצית הגל [math]\displaystyle{ u_n(x)=e^{2\pi i n\frac{t}{N}x} }[/math].
- נציב בה את נקודות הדגימה ונקבל את הוקטור המרוכב:
- [math]\displaystyle{ v_n= \left(u_n(0),u_n(\frac{1}{t}),...,u_n(\frac{N-1}{t})\right) = \left( 1,e^{2\pi i n \frac{1}{N}},e^{2\pi i n \frac{2}{N}},...,e^{2\pi i n \frac{N-1}{N}} \right) }[/math]
- נציב בפונקציה הנתונה f את נקודות הדגימה ונקבל את הוקטור המרוכב:
- [math]\displaystyle{ v=\left(f(0),f(\frac{1}{t}),f(\frac{2}{t}),...,f(\frac{N-1}{t})\right) = (a_0,...,a_{N-1}) }[/math]
- לכן אנו מעוניינים בפתרון למשוואה:
- [math]\displaystyle{ v=B_0v_0+...+B_{N-1}v_{N-1} }[/math]
- זה בדיוק אומר שהפירוק של הפונקציה לגלים מתקיים בכל נקודות הדגימה:
- [math]\displaystyle{ f(\frac{k}{t}) = B_0u_0(\frac{k}{t})+...+B_{N-1}u_{N-1}(\frac{k}{t}) }[/math]
- נבחן את הקבוצה [math]\displaystyle{ \{v_0,...,v_{N-1}\} }[/math].
- [math]\displaystyle{ \langle v_n,v_n\rangle = v_n^t \overline{v_n} = \sum_{k=0}^{N-1} e^{2\pi i n \frac{k}{N}}\cdot e^{-2\pi i n \frac{k}{N}}= 1+1+...+1= N }[/math]
- עבור [math]\displaystyle{ n\neq m }[/math]:
- [math]\displaystyle{ \langle v_n,v_m\rangle = \sum_{k=0}^{N-1} e^{2\pi i n \frac{k}{N}}\cdot e^{-2\pi i m \frac{k}{N}} = \sum_{k=0}^{N-1} e^{2\pi i (n-m) \frac{k}{N}} }[/math]
- אבל זה בדיוק סכום סדרה הנדסית [math]\displaystyle{ 1+q+...+q^{N-1} }[/math] עבור [math]\displaystyle{ q=e^{2\pi i (n-m)\frac{1}{N}} }[/math]
- שימו לב ש[math]\displaystyle{ \frac{|n-m|}{N}\lt 1 }[/math] ולכן [math]\displaystyle{ q\neq 1 }[/math].
- כמו כן, שימו לב ש[math]\displaystyle{ q^N = e^{2\pi i (n-m)}=1 }[/math]
- לכן לפי הנוסחא לסכום סדרה הנדסית נקבל כי:
- [math]\displaystyle{ \langle v_n,v_m\rangle = \frac{1-q^N}{1-q}=0 }[/math]
- כלומר גילינו כי [math]\displaystyle{ \{v_0,...,v_{N-1}\} }[/math] קבוצה אורתוגונלית (לא אורתונורמלית) ומהווה בסיס.
- לכן ניתן בקלות לחשב את המקדמים [math]\displaystyle{ B_n = \frac{\langle v,v_n\rangle}{N} }[/math]
- לבסוף, נשים לב כי:
- [math]\displaystyle{ \langle v,v_n\rangle = \sum_{k=0}^{N-1} a_k e^{-2\pi i n \frac{k}{N}} = A_n }[/math]
- כלומר [math]\displaystyle{ B_n = \frac{A_n}{N} }[/math]
התמרת פורייה הבדידה ההפוכה
- מכאן גם ניתן להסיק ישירות את התמרת פורייה ההפוכה, שמחזירה את סדרת המקדמים [math]\displaystyle{ A_n }[/math] לסדרת הדגימות [math]\displaystyle{ a_n }[/math].
- [math]\displaystyle{ v=\frac{1}{N}(A_0v_0+...+A_{N-1}v_{N-1}) }[/math]
- ולכן:
- [math]\displaystyle{ a_n = \frac{1}{N}\sum_{k=0}^{N-1} A_k e^{2\pi i k \frac{n}{N}} }[/math]
מסקנות לגבי גלים ממשיים
- פירקנו את הפונקציה לסכום של גלים מרוכבים בנקודות הדגימה, האם ניתן להשתמש בהתמרה על מנת לקבל פירוק לגלים ממשיים?
- ראשית, נשים לב לתופעה הבאה:
- [math]\displaystyle{ v_{N-n} = (1,e^{2\pi i (N-n) \frac{1}{N}},...,e^{2\pi i (N-n) \frac{N-1}{N}}) = (1,e^{2\pi i (N-n) \frac{1}{N} - 2\pi i },...,e^{2\pi i (N-n) \frac{N-1}{N} - 2\pi i (N-1)}) }[/math]
- (השיוויון נכון בזכות המחזוריות)
- ולכן נקבל:
- [math]\displaystyle{ v_{N-n} = (1, e^{2\pi i (\frac{(N-n)}{N} - 1)},...,e^{2\pi i (N-1)(\frac{(N-n)}{N} - 1)}) = v_{-n} }[/math]
- כלומר פירוק הפונקציה לגלים [math]\displaystyle{ u_0,u_1,...,u_{N-1} }[/math] נותן את אותם המקדמים כמו פירוק הפונקציה לגלים [math]\displaystyle{ u_0,u_1,u_{-1},... }[/math].
- כאשר המקדם של [math]\displaystyle{ u_{-n} }[/math] שווה למקדם של [math]\displaystyle{ u_{N-n} }[/math].
- שימו לב שזה לא פירוק של הפונקציה לסכום הגלים בכל הממשיים, אלא רק בנקודות הדגימה.
- לדוגמא:
- נניח שיש לנו 5 דגימות של f.
- אם נפרק את f לגלים [math]\displaystyle{ u_0,u_1,...,u_5 }[/math] נקבל [math]\displaystyle{ v=B_0v_0+...+B_4v_4 }[/math]
- אם נפרק את f לגלים [math]\displaystyle{ u_{-2},u_{-1},u_0,u_1,u_2 }[/math] נקבל [math]\displaystyle{ v=B_3v_{-2},B_4v_{-1}+B_0v_0+B_1v_1+B_2v_2 }[/math]
- במצב זה, אם דגמנו בתדר [math]\displaystyle{ t }[/math] נקבל את התדרים [math]\displaystyle{ 0,\frac{t}{5},\frac{2t}{5} }[/math] שזה מתאים למשפט הדגימה של שנון (טווח התדרים של הפונקציה הוא עד חצי מתדר הדגימה).
- עבור n ספציפי מתקיים כי:
- [math]\displaystyle{ B_ne^{2\pi i n \frac{t}{N}x} + B_{N-n}e^{-2\pi i n \frac{t}{N}x} = (B_n+B_{N-n}) \cos (2\pi n \frac{t}{N}x) + i(B_n-B_{N-n})sin(2\pi n \frac{t}{N}x) }[/math]
- מהצבה ישירה של הנוסחאות שמצאנו ניתן לראות שאם f ממשית אזי [math]\displaystyle{ B_n+B_{N-n} }[/math] וגם [math]\displaystyle{ i(B_n-B_{N-n}) }[/math] הם ממשיים.
- כלומר הצלחנו לפרק את f לסכום של גלים ממשיים עם מקדמים ממשיים.
- הערה: אם N זוגי, אז הגל [math]\displaystyle{ u_{\frac{N}{2}} }[/math] נותר בודד.
- לדוגמא עבור [math]\displaystyle{ N=4 }[/math] נקבל במקום הגלים [math]\displaystyle{ u_0,u_1,u_2,u_3 }[/math] את [math]\displaystyle{ u_{-1},u_0,u_1,u_2 }[/math]
- נשים לב כי במקרה זה [math]\displaystyle{ v_{\frac{N}{2}} }[/math] הוא וקטור ממשי (ולכן גם המקדם שלו ממשי) כיוון שהsin מתאפס בכל נקודות הדגימה.