הבדלים בין גרסאות בדף "חקירת פונקציות"
אחיה בר-און (שיחה | תרומות) |
יהודה שמחה (שיחה | תרומות) |
||
| (5 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 15: | שורה 15: | ||
[[מדיה : infi2FuncInvestigationAddional1.pdf | הסברים ותרגילים על חקירת פונקציות]] | [[מדיה : infi2FuncInvestigationAddional1.pdf | הסברים ותרגילים על חקירת פונקציות]] | ||
| − | == תרגילים == | + | ==תרגילים== |
| − | ===דוגמא | + | ===דוגמא 1: <math>f(x)=x^2-6x+5</math>=== |
| − | + | ====תחום הגדרה==== | |
| + | הגדרה: תהי <math>f(x)</math> פונקציה. תחום הגדרתה היא <math>A</math> - אוסף כל הנקודות בהם <math>f(x)</math> מוגדרת. | ||
| − | תחום | + | דוגמא: תחום ההגדרה של <math>f(x)</math> הוא כל הישר <math>\R</math> . |
| − | הגדרה: <math> | + | ====זוגיות/אי-זוגיות==== |
| − | + | הגדרה: <math>f(x)</math> תקרא '''זוגית''' אם <math>f(-x)=f(x)</math> . | |
| − | + | ||
| − | + | הגדרה: <math>f(x)</math> תקרא אי-זוגית אם <math>f(-x)=-f(x)</math> . | |
| − | + | ||
| − | + | ||
| − | + | דוגמא: <math>f(-x)=x^2+6x+5\not=\ \pm\ f(x)</math> ולכן <math>f(x)</math> אינה זוגית ואינה אי-זוגית. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | דוגמא: <math>f(-x)=x^ | + | |
| − | אינה זוגית ואינה אי זוגית | + | |
====חיתוך עם הצירים==== | ====חיתוך עם הצירים==== | ||
| − | + | החיתוך עם ציר <math>x</math> הן הנקודות <math>(1,0)\ ,\ (5,0)</math> | |
| − | החיתוך עם ציר x הן הנקודות <math>(1,0) | + | |
| − | החיתוך עם ציר y היא הנקודה <math>(0,5)</math> | + | החיתוך עם ציר <math>y</math> היא הנקודה <math>(0,5)</math> . |
====נקודות קיצון ותחומי עליה/ירידה==== | ====נקודות קיצון ותחומי עליה/ירידה==== | ||
| + | הגדרה: תהא <math>f(x)</math> פונקציה. נאמר כי <math>f(x)</math> עולה (יורדת) בתחום <math>U</math> אם | ||
| + | |||
| + | <math>\forall x<y\in U:\ f(x)\le f(y)</math> או <math>\forall x<y\in U:\ f(x)\ge f(y)</math> . | ||
| − | הגדרה: | + | הגדרה: תהי <math>f(x)</math> פונקציה. <math>x_0</math> תקרא נקודת קיצון - מקס' (או מינ') אם קיימת לה סביבה <math>U</math> כך ש- |
| − | אם <math> | + | |
| − | + | ||
| − | + | <math>\forall x\in U:f(x)\le f(x_0)</math> או <math>\forall x\in U:f(x)\ge f(x_0)</math> . | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | משפט: אם <math>f(x)</math> | + | משפט: אם <math>f(x)</math> גזירה בנקודת קיצון <math>x_0</math> אזי <math>f'(x_0)=0</math> . |
| − | גזירה בנקודת קיצון <math> | + | |
| − | אזי <math>f'( | + | |
| + | מסקנה: כדי למצוא נקודות קיצון של <math>f(x)</math> מספיק לבדוק מתי <math>f'(x)=0</math> או מתי הנגזרת אינה קיימת כלל. | ||
| − | + | דוגמא - נמצא את הנקודות האפשריות לנקודות קיצון ל- <math>f(x)</math> : | |
| − | + | ||
| − | + | ||
| − | + | <math>f'(x)=2x-6</math> ולכן הנקודה החשודה היחידה היא <math>x_0=3</math> . | |
| − | + | ||
| − | <math>f'(x)=2x-6</math> ולכן הנקודה החשודה היחידה היא <math> | + | |
====מקס' או מיני'==== | ====מקס' או מיני'==== | ||
| − | |||
איך יודעים אם מדובר בנקודות קיצון ואם מדובר בקיצון מקס' או בקיצון מיני'? | איך יודעים אם מדובר בנקודות קיצון ואם מדובר בקיצון מקס' או בקיצון מיני'? | ||
| − | *בדיקת | + | *בדיקת הפונקציה עצמה - הנקודות החשודות מחלקות את הישר לקטעים. נציב בכל קטע נקודה ונבדוק מה מתקבל: למשל נציב <math>f(0)=5\ ,\ f(3)=-4\ ,\ f(6)=5</math> ולכן 3 נקודות מיני'. |
| − | ולכן 3 | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | נקודות מיני' | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | הערה: אכן מספיק לבדוק | + | הערה: אכן מספיק לבדוק נקודות אלו - כי אם הפונקציה היתה מחליפה מיקום (ביחס לנקודות החשודות) היכן שהוא אזי היתה נוצרת נקודת קיצון והיינו מגלים אותה בשלב הקודם. |
| − | * | + | *בדיקת ערכי הנגזרת - נבדוק את סימן הנגזרת מימין ומשמאל לנקודות (מסתמך על העובדה כי: אם <math>f'(x)\le0</math> בקטע <math>I</math> אזי הפונקציה יורדת שם. אם <math>f'(x)\ge0</math> אז הפונקציה עולה שם): <math>f'(0)<0\ ,\ f'(4)>0</math> ולכן משמאל ל-3 הפונקציה יורדת ומימין ל-3 היא עולה, כלומר <math>x=3</math> נקודת מיני'. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | הערה: בשלב זה מצב כי תחום העליה של <math>f</math> הוא <math>[3,\infty)</math> ותחום הירידה <math>(-\infty,3]</math> . | |
| + | הערה: אכן מספיק לבדוק נקו' אלו - כי אם הנגזרת היתה מחליפה היכן שהוא את סימנה אזי היתה נוצרת נקודת קיצון והיינו מגלים אותה בשלב הקודם. | ||
| − | = | + | *מבחן הנגזרת השניה - אם <math>f'(x_0)=0</math> ומתקיים <math>f''(x_0)>0</math> (או <math>f''(x)<0</math>) אז <math>x_0</math> נקודות מיני' (או מקס'): |
| − | + | אצלנו <math>f''(x)=2</math> ולכן <math>f''(2)>0</math> . | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | <math>f(x) | + | ====תחומי קעירות/קמירות ונקודות פיתול==== |
| + | תהא <math>f(x)</math> גזירה בנקודה <math>x_0</math> אזי נאמר שהפונקציה קעורה כלפי מעלה/מטה ב- <math>x_0</math> אם קיימת סביבה <math>U</math> של <math>x_0</math> כך שלכל <math>x\in U</math> מתקיים: | ||
| − | + | <math>f(x)\ge f'(x_0)(x-x_0)+f(x_0)</math> או <math>f(x)\le f'(x_0)(x-x_0)+f(x_0)</math> . | |
| + | נאמר כי <math>x_0</math> נקודת פיתול אם קיימת סביבה <math>U</math> ימנית בה <math>f(x)\ge f'(x_0)(x-x_0)+f(x_0)</math> וסביבה שמאלית <math>V</math> בה <math>f(x)\le f'(x_0)(x-x_0)+f(x_0)</math> או להפך. | ||
| − | + | משפט: <math>f''(x_0)>0</math> או <math>f''(x_0)<0</math> אז <math>f(x)</math> קעורה כלפי מעלה/מטה ב- <math>x_0</math> . | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | משפט: <math>f | + | משפט: הנקודות החשודות לפיתול הם הנקודות בהם <math>f''(x)</math> אינה קיימת או ש- <math>f''(x)=0</math> . |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | דוגמא: <math>f''(x)=2</math> ולכן אין נקודות פיתול והפונקציה קעורה כלפי מעלה בכל הישר. | |
| − | + | ||
| − | + | ||
| − | + | ====אסימפטוטות==== | |
| − | + | הגדרה: אסימפטוטה אנכית ל- <math>f(x)</math> היא קו מהצורה <math>x=a</math> כך שמתקיים <math>\lim\limits_{x\to a}|f(x)|=\infty</math> . אצלנו אין אסימפטוטה אנכית. | |
| − | + | הגדרה: אסימפטוטה אופקית היא ישר <math>l(x)=ax+b</math> המקיים <math>\lim\limits_{x\to\infty}\Big|f(x)-l(x)\Big|=0</math> או <math>\lim\limits_{x\to-\infty}\Big|f(x)-l(x)\Big|=0</math> . | |
| − | + | איך מוצאים? מתקיים <math>a=\lim\limits_{x\to\infty}\dfrac{f(x)}{x}</math> ואז <math>b=\lim\limits_{x\to\infty}\big[f(x)-ax\big]</math> . | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | אצלנו | + | דוגמא - אצלנו: |
| − | + | <math>\displaystyle a=\lim_{x\to\infty}\frac{f(x)}{x}=\lim_{x\to\infty}\frac{x^2-6x+5}{x}=\infty</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ולכן אין אסימפטוטה אופקית. | |
| − | + | ====התנהגות הפונקציה באינסוף==== | |
| − | + | עבור הדוגמא שלנו <math>\lim\limits_{x\to\pm\infty}f(x)=\infty</math> | |
| − | + | ציור הפונקציה [[קובץ:Example1CStirgul2.gif]] | |
| − | + | ||
| − | + | ===דוגמא 2: <math>f(x)=\dfrac{\ln(x)}{x}</math>=== | |
| − | + | ====תחום הגדרה==== | |
| − | + | <math>x>0</math> כי <math>\ln(x)</math> לא-מוגדרת עבור <math>x</math>-ים שליליים. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | דוגמא 2: f(x)=\ | + | |
| − | + | ||
| − | + | ||
| − | תחום הגדרה | + | |
| − | + | ||
| − | x>0 | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | ====זוגיות/אי-זוגיות==== | ||
לא שייך בגלל תחום ההגדרה. | לא שייך בגלל תחום ההגדרה. | ||
| − | חיתוך עם הצירים | + | ====חיתוך עם הצירים==== |
| + | החיתוך עם ציר <math>x</math> הוא <math>(1,0)</math> . | ||
| − | החיתוך עם ציר | + | החיתוך עם ציר <math>y</math> לא קיים בגלל תחום ההגדרה. |
| − | + | ||
| − | + | ||
| − | + | ====נקודות קיצון ותחומי עליה/ירידה==== | |
| − | + | <math>f'(x)=\dfrac{1-\ln(x)}{x^2}</math> לכן יש לה נקודה חשודה ב- <math>x=e</math> | |
| − | + | הסימן של <math>f''</math> נקבע ע"י <math>-x-2x\big(1-\ln(x)\big)=-x\big(3-2\ln(x)\big)</math> . | |
| − | f | + | <math>f(e)<0</math> ולכן זוהי נקודת מקס'. |
| − | + | ||
| − | + | ||
| − | + | תחומי העליה של הפונקציה <math>(0,e)</math> . | |
| − | + | ||
| − | + | ||
| − | + | תחומי הירידה <math>(e,\infty)</math> . | |
| − | + | ||
| − | תחומי | + | ====תחומי קעירות/קמירות ונקודות פיתול==== |
| − | + | הסימן של <math>f''</math> נקבע ע"י <math>-x\big(3-2\ln(x)\big)</math> ולכן נקודות חשודות לפיתול הם <math>e\sqrt{e}</math> . | |
| − | + | <math>f''(e)<0\ ,\ f''(e^4)>0</math> ולכן <math>e\sqrt{e}\approx 10</math> נקודת פיתול. | |
| − | + | ||
| − | + | הפונקציה קעורה כלפי מטה ב- <math>(0,e\sqrt{e})</math> . | |
| − | + | הפונקציה קעורה כלפי מעלה ב- <math>(e\sqrt{e},\infty)</math> . | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ====אסימפטוטות==== | |
| − | + | אסימפטוטה אנכית ב- <math>x=0</math> כיון ש- <math>\lim\limits_{x\to0^+}f(x)=-\infty</math> . | |
| − | + | ||
| − | + | אסימפטוטה אופקית: | |
| − | + | ||
| − | + | <math>\begin{align}\displaystyle a=\lim_{x\to\infty}\frac{f(x)}{x}=\lim_{x\to\infty}\frac{\ln(x)}{x^2}=\lim_{x\to\infty}\frac{\frac1x}{2x}=0\\b=\lim_{x\to\infty}\big[f(x)-ax\big]=\lim_{x\to}\frac{\ln(x)}{x}=0\end{align}</math> | |
| − | + | ||
| − | + | ולכן <math>l(x)=0</math> אסימטוטה אופקית. | |
| − | + | ====התנהגות הפונקציה באינסוף==== | |
| − | + | עבור הדוגמא שלנו <math>\lim\limits_{x\to\infty}f(x)=0</math> | |
| − | + | ||
| − | + | ציור הפונקציה [[קובץ:Example2CStirgul2.gif]] | |
| − | + | ===דוגמא 3: <math>f(x)=\dfrac{x^3}{12-x^2}</math>=== | |
| − | + | ====תחום הגדרה==== | |
| + | <math>x\ne\pm2\sqrt3</math> | ||
| − | + | ====זוגיות/אי-זוגיות==== | |
| − | + | <math>f(-x)=\dfrac{-x^3}{12-x^2}=-f(x)</math> ולכן <math>f(x)</math> אי-זוגית. | |
| − | + | ===נקודות קיצון=== | |
| − | + | <math>f'(x)=\dfrac{3x^2(12-x^2)+2x^4}{(12-x^2)^2}=\dfrac{x^2(36-x^2)}{(12-x^2)^{2}}</math> ולכן הנקודות החשודות הן <math>x_0=0,\pm6,\pm2\sqrt3</math> | |
| − | + | (נשים לב שהנקודות <math>\pm2\sqrt3</math> אינן נקודות קיצון כי אינן בתחום ההגדרה). | |
| − | + | =====מקס' או מיני'===== | |
| − | + | נשים לב שסימן הנגזרת נקבע לפי החלק של <math>36-x^2</math> : | |
| − | + | <math>\begin{align}f'(-7)<0\\f'(-6)=0\\f'(-4)>0\\f'(-1)>0\\f'(0)=0\\f'(4)>0\\f'(6)=0\\f'(7)<0\end{align}</math> | |
| + | ולכן משמאל ל-'''6-''' הפונקציה יורדת ומימין ל-'''6-''' היא עולה, כלומר '''6-''' נקודות מיני'. | ||
| + | 6 נקודת מקס'. | ||
| − | + | 0 אינה נקודת קיצון כי הפונקציה עולה גם מימין לה וגם משמאל. | |
| − | + | ||
| − | + | ====תחומי קעירות/קמירות ונקודות פיתול==== | |
| + | דוגמא: | ||
| − | + | <math>\begin{align}f(x)&=\dfrac{x^3}{12-x^2}\\f'(x)&=\dfrac{3x^2(12-x^2)+2x^4}{(12-x^2)^2}=\dfrac{x^2(36-x^2)}{(12-x^2)^2}\\f''(x)&=\dfrac{24x(12-x^2)(36+x^2)}{(12-x^2)^4}\end{align}</math> | |
| − | + | ||
| − | + | הנקודות החשודות לפיתול הן <math>0,\pm2\sqrt3</math> . הסימן של <math>f''(x)</math> נקבע לפי החלק <math>x(12-x^2)</math> . | |
| − | + | נבדוק: | |
| − | + | ||
| − | + | ||
| − | + | <math>\begin{align}f''(-4)>0\\f''(-1)<0\\f(0)=0\\f(1)>0\\f(4)<0\end{align}</math> | |
| − | + | ומכאן מסיקים כי - | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | בקטע <math>(-\infty,-2\sqrt3)</math> הפונקציה קעורה כלפי מעלה, | |
| − | + | בקטע <math>(-2\sqrt3,0)</math> הפונקציה קעורה כלפי מטה, | |
| − | + | בקטע <math>(0,2\sqrt3)</math> הפונקציה קעורה כלפי מעלה, | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | בקטע <math>(2\sqrt3,\infty)</math> הפונקציה קעורה כלפי מטה, | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ובנקודה 0 יש נקודות פיתול (כי הנגזרת השניה שלילית עד אליה וחיובית ממנה). | |
| − | + | ====אסימפטוטות==== | |
| − | + | ל- <math>f(x)=\frac{x^3}{12-x^2}</math> יש 2 אסימפטוטות אנכיות ב- <math>x=\pm2\sqrt3</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | כי <math>\lim\limits_{x\to{-2\sqrt3}^+}f(x)=\lim\limits_{x\to{2\sqrt3}^+}f(x)=-\infty</math> | |
| − | + | <math>\lim\limits_{x\to{-2\sqrt3}^-}f(x)=\lim\limits_{x\to{2\sqrt3}^-}f(x)=\infty</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | אסימפטוטה אופקית: | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | <math>\displaystyle\begin{align}a=\lim_{x\to\infty}\frac{f(x)}{x}=\lim_{x\to\infty}\frac{x^3}{x(12-x^2)}=-1\\b=\lim_{x\to\infty}\left[\frac{x^3}{12-x^2}+x\right]=\lim_{x\to\infty}\frac{12x}{12-x^2}=0\end{align}</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | b=lim_{x\to\infty} | + | |
| + | באותו אופן גם אסימפטוטה לכיוון <math>x\to-\infty</math> תצא אותו דבר | ||
| − | + | ולכן <math>l(x)=-x</math> אסימפטוטה אופקית לשני הצדדים. | |
| − | + | ||
| − | + | ====התנהגות הפונקציה באינסוף==== | |
| − | + | עבור הדוגמא שלנו <math>\displaystyle\lim_{x\to\infty}\frac{x^3}{12-x^2}=\infty\ ,\ \lim_{x\to-\infty}\frac{x^3}{12-x^2}=-\infty</math> | |
| − | + | ====ציור הפונקציה==== | |
| + | [[קובץ:Examp3e2CStirgul2.gif]] | ||
| − | + | משפטים לסיכום: | |
| − | + | ||
| − | + | '''1)''' אם <math>f(x)</math> גזירה בנקודת קיצון <math>x_0</math> אזי <math>f'(x_0)=0</math> . | |
| + | '''2)''' מבחן הנגזרת השניה - אם <math>f'(x_0)=0</math> ומתקיים <math>f''(x_0)>0</math> אזי <math>x_0</math> נקודת מיני'. | ||
| + | '''3)''' אם <math>f'(x)\le0</math> בקטע <math>I</math> אזי הפונקציה יורדת שם. אם <math>f'(x)\ge0</math> אזי הפונקציה עולה שם. | ||
| − | + | '''4)''' אם <math>f''(x_0)>0</math> אזי <math>f(x)</math> קעורה כלפי מעלה ב- <math>x_0</math> . | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | . | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | מסקנה: הנקודות החשודות לפיתול הם הנקודות בהם <math>f''(x)</math> אינה קיימת או ש- <math>f''(x)=0</math> . | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
גרסה אחרונה מ־01:10, 13 בפברואר 2017
נושא חקירת פונקציות בקורס חשבון אינפיניטיסימלי כוללת מחקר סט תכונות מוסכם (פחות או יותר):
- תחום הגדרה (קביעה באילו נקודות הפונקציה מוגדרת)
- זוגיות (קביעה האם הפונקציה זוגית, אי-זוגית או לא)
- תחומי מונוטוניות ומציאת נקודות קיצון
- תחומי קמירות ומציאת נקודות פיתול
- אסימפטוטות מאונכות
- נקודות חיתוך עם הצירים
- אסימפטוטות משופעות ומציאת התנהגות באינסוף
- תרפיה בתרשים- ציור גרף הפונקציה
הסברים ותרגילים על חקירת פונקציות
תוכן עניינים
תרגילים
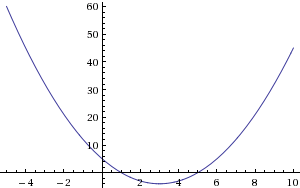
דוגמא 1: 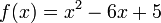
תחום הגדרה
הגדרה: תהי  פונקציה. תחום הגדרתה היא
פונקציה. תחום הגדרתה היא  - אוסף כל הנקודות בהם
- אוסף כל הנקודות בהם  מוגדרת.
מוגדרת.
דוגמא: תחום ההגדרה של  הוא כל הישר
הוא כל הישר 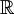 .
.
זוגיות/אי-זוגיות
הגדרה:  תקרא זוגית אם
תקרא זוגית אם 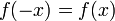 .
.
הגדרה:  תקרא אי-זוגית אם
תקרא אי-זוגית אם 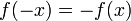 .
.
דוגמא: 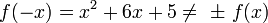 ולכן
ולכן  אינה זוגית ואינה אי-זוגית.
אינה זוגית ואינה אי-זוגית.
חיתוך עם הצירים
החיתוך עם ציר  הן הנקודות
הן הנקודות 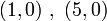
החיתוך עם ציר  היא הנקודה
היא הנקודה 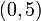 .
.
נקודות קיצון ותחומי עליה/ירידה
הגדרה: תהא  פונקציה. נאמר כי
פונקציה. נאמר כי  עולה (יורדת) בתחום
עולה (יורדת) בתחום 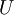 אם
אם
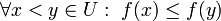 או
או 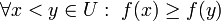 .
.
הגדרה: תהי  פונקציה.
פונקציה.  תקרא נקודת קיצון - מקס' (או מינ') אם קיימת לה סביבה
תקרא נקודת קיצון - מקס' (או מינ') אם קיימת לה סביבה 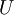 כך ש-
כך ש-
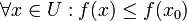 או
או 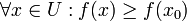 .
.
משפט: אם  גזירה בנקודת קיצון
גזירה בנקודת קיצון  אזי
אזי 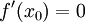 .
.
מסקנה: כדי למצוא נקודות קיצון של  מספיק לבדוק מתי
מספיק לבדוק מתי 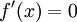 או מתי הנגזרת אינה קיימת כלל.
או מתי הנגזרת אינה קיימת כלל.
דוגמא - נמצא את הנקודות האפשריות לנקודות קיצון ל-  :
:
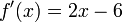 ולכן הנקודה החשודה היחידה היא
ולכן הנקודה החשודה היחידה היא 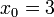 .
.
מקס' או מיני'
איך יודעים אם מדובר בנקודות קיצון ואם מדובר בקיצון מקס' או בקיצון מיני'?
- בדיקת הפונקציה עצמה - הנקודות החשודות מחלקות את הישר לקטעים. נציב בכל קטע נקודה ונבדוק מה מתקבל: למשל נציב
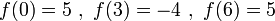 ולכן 3 נקודות מיני'.
ולכן 3 נקודות מיני'.
הערה: אכן מספיק לבדוק נקודות אלו - כי אם הפונקציה היתה מחליפה מיקום (ביחס לנקודות החשודות) היכן שהוא אזי היתה נוצרת נקודת קיצון והיינו מגלים אותה בשלב הקודם.
- בדיקת ערכי הנגזרת - נבדוק את סימן הנגזרת מימין ומשמאל לנקודות (מסתמך על העובדה כי: אם
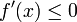 בקטע
בקטע 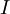 אזי הפונקציה יורדת שם. אם
אזי הפונקציה יורדת שם. אם 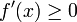 אז הפונקציה עולה שם):
אז הפונקציה עולה שם): 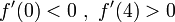 ולכן משמאל ל-3 הפונקציה יורדת ומימין ל-3 היא עולה, כלומר
ולכן משמאל ל-3 הפונקציה יורדת ומימין ל-3 היא עולה, כלומר 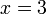 נקודת מיני'.
נקודת מיני'.
הערה: בשלב זה מצב כי תחום העליה של  הוא
הוא 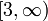 ותחום הירידה
ותחום הירידה ![(-\infty,3]](/images/math/a/3/4/a344f5a460db11b3918099de2a61ab0d.png) .
.
הערה: אכן מספיק לבדוק נקו' אלו - כי אם הנגזרת היתה מחליפה היכן שהוא את סימנה אזי היתה נוצרת נקודת קיצון והיינו מגלים אותה בשלב הקודם.
- מבחן הנגזרת השניה - אם
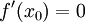 ומתקיים
ומתקיים 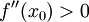 (או
(או 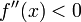 ) אז
) אז  נקודות מיני' (או מקס'):
נקודות מיני' (או מקס'):
אצלנו 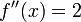 ולכן
ולכן 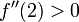 .
.
תחומי קעירות/קמירות ונקודות פיתול
תהא  גזירה בנקודה
גזירה בנקודה  אזי נאמר שהפונקציה קעורה כלפי מעלה/מטה ב-
אזי נאמר שהפונקציה קעורה כלפי מעלה/מטה ב-  אם קיימת סביבה
אם קיימת סביבה 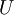 של
של  כך שלכל
כך שלכל 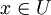 מתקיים:
מתקיים:
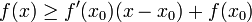 או
או 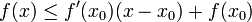 .
.
נאמר כי  נקודת פיתול אם קיימת סביבה
נקודת פיתול אם קיימת סביבה 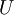 ימנית בה
ימנית בה 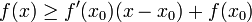 וסביבה שמאלית
וסביבה שמאלית  בה
בה 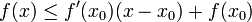 או להפך.
או להפך.
משפט: 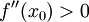 או
או 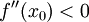 אז
אז  קעורה כלפי מעלה/מטה ב-
קעורה כלפי מעלה/מטה ב-  .
.
משפט: הנקודות החשודות לפיתול הם הנקודות בהם 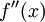 אינה קיימת או ש-
אינה קיימת או ש- 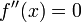 .
.
דוגמא: 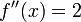 ולכן אין נקודות פיתול והפונקציה קעורה כלפי מעלה בכל הישר.
ולכן אין נקודות פיתול והפונקציה קעורה כלפי מעלה בכל הישר.
אסימפטוטות
הגדרה: אסימפטוטה אנכית ל-  היא קו מהצורה
היא קו מהצורה 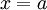 כך שמתקיים
כך שמתקיים 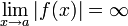 . אצלנו אין אסימפטוטה אנכית.
. אצלנו אין אסימפטוטה אנכית.
הגדרה: אסימפטוטה אופקית היא ישר 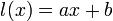 המקיים
המקיים 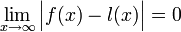 או
או 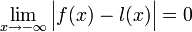 .
.
איך מוצאים? מתקיים 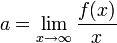 ואז
ואז ![b=\lim\limits_{x\to\infty}\big[f(x)-ax\big]](/images/math/e/3/a/e3afbef07df28812ce2b3deac4eb992b.png) .
.
דוגמא - אצלנו:
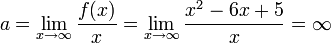
ולכן אין אסימפטוטה אופקית.
התנהגות הפונקציה באינסוף
עבור הדוגמא שלנו 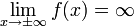
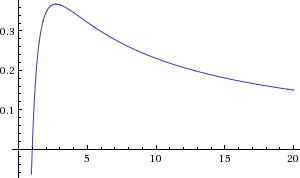
דוגמא 2: 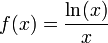
תחום הגדרה
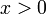 כי
כי 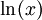 לא-מוגדרת עבור
לא-מוגדרת עבור  -ים שליליים.
-ים שליליים.
זוגיות/אי-זוגיות
לא שייך בגלל תחום ההגדרה.
חיתוך עם הצירים
החיתוך עם ציר  הוא
הוא 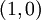 .
.
החיתוך עם ציר  לא קיים בגלל תחום ההגדרה.
לא קיים בגלל תחום ההגדרה.
נקודות קיצון ותחומי עליה/ירידה
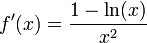 לכן יש לה נקודה חשודה ב-
לכן יש לה נקודה חשודה ב- 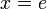
הסימן של 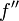 נקבע ע"י
נקבע ע"י 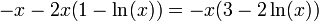 .
.
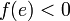 ולכן זוהי נקודת מקס'.
ולכן זוהי נקודת מקס'.
תחומי העליה של הפונקציה 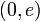 .
.
תחומי הירידה 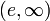 .
.
תחומי קעירות/קמירות ונקודות פיתול
הסימן של 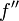 נקבע ע"י
נקבע ע"י 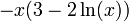 ולכן נקודות חשודות לפיתול הם
ולכן נקודות חשודות לפיתול הם 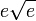 .
.
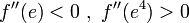 ולכן
ולכן 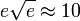 נקודת פיתול.
נקודת פיתול.
הפונקציה קעורה כלפי מטה ב- 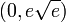 .
.
הפונקציה קעורה כלפי מעלה ב- 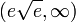 .
.
אסימפטוטות
אסימפטוטה אנכית ב- 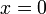 כיון ש-
כיון ש- 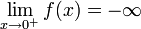 .
.
אסימפטוטה אופקית:
![\begin{align}\displaystyle a=\lim_{x\to\infty}\frac{f(x)}{x}=\lim_{x\to\infty}\frac{\ln(x)}{x^2}=\lim_{x\to\infty}\frac{\frac1x}{2x}=0\\b=\lim_{x\to\infty}\big[f(x)-ax\big]=\lim_{x\to}\frac{\ln(x)}{x}=0\end{align}](/images/math/f/a/0/fa0a8d7523357e71d2de394f943aa762.png)
ולכן 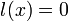 אסימטוטה אופקית.
אסימטוטה אופקית.
התנהגות הפונקציה באינסוף
עבור הדוגמא שלנו 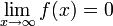
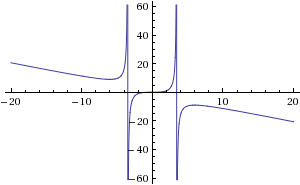
דוגמא 3: 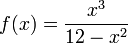
תחום הגדרה
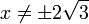
זוגיות/אי-זוגיות
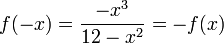 ולכן
ולכן  אי-זוגית.
אי-זוגית.
נקודות קיצון
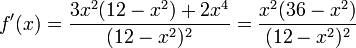 ולכן הנקודות החשודות הן
ולכן הנקודות החשודות הן 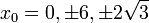
(נשים לב שהנקודות 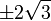 אינן נקודות קיצון כי אינן בתחום ההגדרה).
אינן נקודות קיצון כי אינן בתחום ההגדרה).
מקס' או מיני'
נשים לב שסימן הנגזרת נקבע לפי החלק של 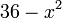 :
:
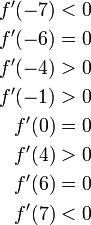
ולכן משמאל ל-6- הפונקציה יורדת ומימין ל-6- היא עולה, כלומר 6- נקודות מיני'.
6 נקודת מקס'.
0 אינה נקודת קיצון כי הפונקציה עולה גם מימין לה וגם משמאל.
תחומי קעירות/קמירות ונקודות פיתול
דוגמא:
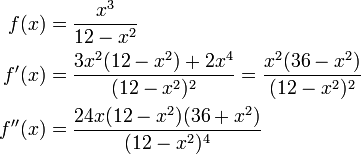
הנקודות החשודות לפיתול הן 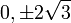 . הסימן של
. הסימן של 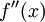 נקבע לפי החלק
נקבע לפי החלק 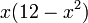 .
.
נבדוק:
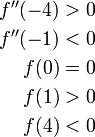
ומכאן מסיקים כי -
בקטע 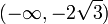 הפונקציה קעורה כלפי מעלה,
הפונקציה קעורה כלפי מעלה,
בקטע 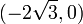 הפונקציה קעורה כלפי מטה,
הפונקציה קעורה כלפי מטה,
בקטע 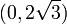 הפונקציה קעורה כלפי מעלה,
הפונקציה קעורה כלפי מעלה,
בקטע 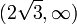 הפונקציה קעורה כלפי מטה,
הפונקציה קעורה כלפי מטה,
ובנקודה 0 יש נקודות פיתול (כי הנגזרת השניה שלילית עד אליה וחיובית ממנה).
אסימפטוטות
ל- 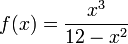 יש 2 אסימפטוטות אנכיות ב-
יש 2 אסימפטוטות אנכיות ב- 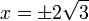
כי 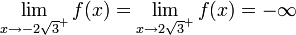
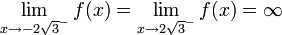
אסימפטוטה אופקית:
![\displaystyle\begin{align}a=\lim_{x\to\infty}\frac{f(x)}{x}=\lim_{x\to\infty}\frac{x^3}{x(12-x^2)}=-1\\b=\lim_{x\to\infty}\left[\frac{x^3}{12-x^2}+x\right]=\lim_{x\to\infty}\frac{12x}{12-x^2}=0\end{align}](/images/math/9/5/c/95c62800138345e08dda9d71e3057f10.png)
באותו אופן גם אסימפטוטה לכיוון 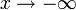 תצא אותו דבר
תצא אותו דבר
ולכן 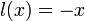 אסימפטוטה אופקית לשני הצדדים.
אסימפטוטה אופקית לשני הצדדים.
התנהגות הפונקציה באינסוף
עבור הדוגמא שלנו 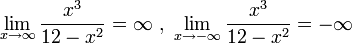
ציור הפונקציה
משפטים לסיכום:
1) אם  גזירה בנקודת קיצון
גזירה בנקודת קיצון  אזי
אזי 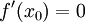 .
.
2) מבחן הנגזרת השניה - אם 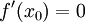 ומתקיים
ומתקיים 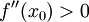 אזי
אזי  נקודת מיני'.
נקודת מיני'.
3) אם 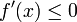 בקטע
בקטע 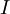 אזי הפונקציה יורדת שם. אם
אזי הפונקציה יורדת שם. אם 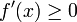 אזי הפונקציה עולה שם.
אזי הפונקציה עולה שם.
4) אם 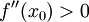 אזי
אזי  קעורה כלפי מעלה ב-
קעורה כלפי מעלה ב-  .
.
מסקנה: הנקודות החשודות לפיתול הם הנקודות בהם 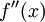 אינה קיימת או ש-
אינה קיימת או ש- 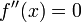 .
.